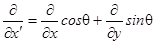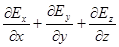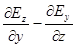Скаляры векторы и псевдовекторы в уравнениях максвелла

максвелла уравнения

МАКСВЕЛЛА УРАВНЕНИЯ

1. Краткая история

2. Каноническая форма

3. Максвелла уравнения в интегральной форме

4. Общая характеристика Максвелла уравнений

5. Максвелла уравнения для комплексных амплитуд

6. Алгебраические Максвелла уравнения

7. Материальные уравнения

8. Граничные условия

9. Двойственная симметрия Максвелла уравнений

10. Максвелла уравнения в четырёхмерном представлении

11. Лоренц-инвариантность Максвелла уравнений

12. Лагранжиан для электромагнитного поля

13. Единственность решений Максвелла уравнений

14. Классификация приближений Максвелла уравнений

15. Максвелла уравнения в различных системах единиц

Максвелла уравнения — ур-ния, к-рым подчиняется (в пределах применимости классической ыакроскопич. электродинамики, см. Электродинамика классическая), электромагнитное поле в вакууме и сплошных средах.

1. Краткая история

Установлению M. у. предшествовал ряд открытий законов взаимодействий заряженных, намагниченных и токонесущих тел (в частности, законов Кулона, Био — Савара, Ампера). В 1831 M. Фарадей (M. Faraday) открыл закон эл—магн. индукции и примерно в то же время ввёл понятие электрич. и магн. полей как самостоят, физ. субстанций. Опираясь на фарадеевское представление о поле и введя ток смещения, равнозначный по своему магн. действию обычному электрич. току, Дж. К. Максвелл (J. С. Maxwell, 1864) сформулировал систему ур-ний, названную впоследствии ур-ниями Максвелла. M. у. функционально связывают электрич. и магн. поля с зарядами и токами и охватывают собой все известные закономерности макроэлектромагнетизма. Впервые о M. у. было доложено на заседании Лондонского Королевского общества 27 окт. 18(34. Первоначально Максвелл прибегал к вспомогат. механич. моделям «эфира», но уже в «Трактате об электричестве и магнетизме» (1873) эл—магн. поле рассматривалось как самостоят, физ. объект. Физ. основа M. у.- принцип близкодействия, утверждающий, что передача эл—магн. возмущений от точки к точке происходит с конечной скоростью (в вакууме со скоростью света с). Он противопоставлялся ньютоновскому принципу дальнодействия, сводящемуся к мгновенной передаче воздействий на любое расстояние Матем. аппаратом теории Максвелла послужил векторный анализ, представленный в инвариантной форме через кватернионы Гамильтона. Сам Максвелл считал, что его заслуга состоит лишь в матем. оформлении идей Фарадея.

2. Каноническая форма

Канонич. форма записи, принятая ныне, принадлежит Г. Герцу (H. Hertz) и О. Хевисайду (О. Heaviside) и основана на использовании не кватернионных, а векторных полей: напряжённости электрического поля E, напряжённости магнитного поля H, векторов электрической индукции D и магнитной индукции В. M. у. связывают их между собой, с плотностью электрического заряда и плотностью электрического тока J, к-рые рассматриваются как источники:

Здесь использована Гаусса система единиц (о записи M. у. в др. системах см. в разделе 15). Входящие в (1) — (4) величины E, D, j являются истинными, или полярными, векторами (а величина r — истинным скаляром), поля H к В — псевдовекторами, или аксиальными векторами. Все эти величины предполагаются непрерывными (вместе со всеми производными) ф-циями времени t и координат Следовательно, в ур-ниях (1) — (4) не учитывается ни дискретная структура электрич. зарядов и токов, ни квантовый характер самих полей. Учёт дискретности истинных источников может быть произведён даже в доквантовом (классич.) приближении с помощью Лоренца — Максвелла уравнений.

3. Максвелла уравнения в интегральной форме

Используя Гаусса — Остроградского формулу и С такса формулу, ур-ниям (1) — (4) можно придать форму интегральных:

Криволинейные интегралы в (1a), (2a) берутся по произвольному замкнутому контуру (их наз. циркуляция-ми векторных полей), а стоящие в правых частях поверхностные интегралы — по поверхностям, ограниченным этими контурами (опирающимся на них), причём направление циркуляции (направление элемента контура) связано с направлением нормали к S (вектор) правовинтовым соотношением (если в качестве исходного выбрано пространство с правыми системами координат). В интегралах по замкнутым поверхностям (S) в (3а), (4а) направление вектора элемента площади совпадает с наружной нормалью к поверхности; V — объём, ограниченный замкнутой поверхностью S.

M. у. в форме (1a) — (4a) предназначаются не только для изучения топологич. свойств эл—магн. полей, но и являются удобным аппаратом решения конкретных задач электродинамики в системах с достаточно высокой симметрией или с априорно известными распределениями полей. Кроме того, в матем. отношении эта система ур-ний содержательнее системы (1) — (4), поскольку пригодна для описания разрывных, нодиффе-ренцируемых распределений полей. Но в отношении физ. пределов применимости обе системы ур-ний равнозначны, т. к. любые скачки полей в макроэлектродинамике должны рассматриваться как пределы микромасштабно плавных переходов, с тем чтобы внутри них сохранялась возможность усреднения ур-ний Лоренца — Максвелла. С этими оговорками резкие скачки можно описывать и в рамках M. у. (1) — (4), прибегая к аппарату обобщённых функций.

Наконец, M. у. в интегральной форме облегчают физ. интерпретацию MH. эл—магн. явлений и поэтому нагляднее сопоставляются с теми экспериментально установленными законами, к-рым они обязаны своим происхождением. Так, ур-ние (1a) есть обобщение Био — Савара закона (с добавлением к току максвелловского смещения тока).

Ур-ние (2a) выражает закон индукции Фарадея; иногда его правую часть переобозначают через «магн. ток смещения»

где— плотность «магн. тока смещения», Ф В — магн. поток. Ур-ние (За) связывают с именем Гаусса , установившим соленоидальность поля В, обусловленную отсутствием истинных магн. зарядов. Впрочем вопрос о существовании магнитных монополей пока остаётся открытым. Но соответствующее обобщение M. у. произведено (Хевисайд, 1885) на основе принципа двойственной симметрии M. у. (см. в разделе 9), для чего в (2) и (2a) наряду с магн. током смещения вводится ещё и «истинный» магн. ток (процедура, обратная проделанной когда-то Максвеллом с электрич. током в первом ур-нии), а в ур-ние Гаусса (3), (За) — магн. заряд

где — плотность магн. заряда. Фактически все экспериментальные установки для регистрации ожидаемых магнитных монополей основаны на этом предположении. Наконец, ур-ние (4a) определяет поле свободного электрич. заряда; его иногда называют законом Кулона (Ch. A. Coulomb), хотя, строго говоря, оно не содержит утверждения о силе взаимодействия между зарядами, да и к тому же справедливо не только в электростатике, но и для систем с произвольным изменением поля во времени. На тех же основаниях иногда и ур-нпе (Ia) связывают с именем Ампера (A. Ampere).

4. Общая характеристика Максвелла уравнений

Совокупность M. у. (1) — (4) составляет систему из восьми (двух векторных и двух скалярных) линейных дифференц. ур-ний 1-го порядка для четырёх векторов Источники (скаляри вектор) не могут быть заданы произвольно; применяя операцию к ур-нию (1) и подставляя результат в (4), получаем:

или в интегральной форме:

Это ур-ние непрерывности для тока, содержащее в себе закон сохранения заряда для замкнутых изолнров. областей,- один из фундам. физ. принципов, подтверждаемых в любых экспериментах.

Ур-ния (1) — (4) распадаются на два самостоят, «блока»: ур-ния (1) и (4), содержащие векторы и источники и ур-ния (2) и (3) — однородные ур-ния для не содержащие источников. Ур-ння (2) и (3) допускают получение общего решения, в к-ромвыражаются через т. H. потенциалы электромагнитного поляПри этом ур-ние (3) «почти следует» из (2), т. к. операция (у), применённая к (2), даёт что отличается от (3) только константой, определяемой нач. условиями. Аналогично ур-ние (4) «почти следует» из (1) и ур-ния непрерывности (5).

Система M. у. (1) — (4) не является полной: по существу, она связывает 4 векторные величины двумя векторными ур-ниями. Её замыкание осуществляется путём добавления соотношений, связывающих векторы 1-го «блока»с векторами 2-го «блока» Эти соотношения зависят от свойств сред (материальных сред), в к-рых происходят эл—магн. процессы, и наз. материальными ур-ниями (см. раздел 7).

5. Максвелла уравнения для комплексных амплитуд

В силу линейности системы (1) — (4) для её решений справедлив суперпозиции принцип .Часто оказывается удобным фурье-представление общего решения (1) — (4) как ф-ции времени (см. Фурье преобразование). Записывая временной фактор в виде , для комплексных фурье-амплитуди т. д.) получаем систему ур-ний

Система (1б) — (4б) в нек-ром смысле удобнее (1) — (4), ибо упрощает применение к эл—динамич. системам, обладающим временной дисперсией (см. раздел 7), т. е. зависимостью параметров от частоты

6. Алгебраические Максвелла уравнения

Если распространить (в силу линейности M. у.) фурье-разложение и на зависимость полей от пространственных координат, т. е. представить общее решение ур-ний (1) — (4) в виде суперпозиции плоских волн типа (k — волновой вектор), то для фурье-компонентов нолейk и т. д.) получим систему алгебраич. ур-ний:

Такое сведение M. у. к набору ур-ний для осцилляторов (осцилляторов поля) составляет важный этап перехода к квантовой электродинамике, где эл—магн. поле рассматривается как совокупность фотонов, характеризуемых энергиями и импульсами Однако и в макроэлектродинамике представления (1в) — (4в) оказываются иногда вполне адекватными физ. сущности процессов: напр., при выделении откликов высокодобротных систем (см. Объёмный резонатор) или при изучении «механизма формирования» мод со сложной пространственной структурой из набора плоских волн и т. п. Наконец, M. у. в форме (1в) — (4в) удобны для описания свойств эл—динамич. систем, обладающих не только временной, но и пространственной дисперсией, если последняя задаётся в виде зависимости параметров от волнового вектора k.

7. Материальные уравнения

В макроэлектродинамике материальные связи, характеризующие эл—магн. свойства сред, вводятся феноменологически; они находятся либо непосредственно из эксперимента, либо на основании модельных представлений. Существуют два способа описания: в одном векторы E и H считаются исходными и материальные ур-ния задаются в виде D = D(E , H) и В = В( Е,Н), в другом — за исходные берутся векторы 2-го «блока» E и В, и соответствующие материальные связи представляются иначе: D = D(E,В), H= H(E, В). Оба описания совпадают для вакуума, где материальные уравнения вырождаются в равенства D = E и B = H.

Рассмотрим простейшую модель среды, характеризуемую мгновенным, локальным поляризац. откликом на появляющиеся в ней поля E и H. Под действием поля E в такой среде возникает электрич. поляризация (см. Поляризации вектор), а под действием поля H — магн. поляризация . Чаще её наз. намагниченностью и обозначают М.

Материальные ур-ния для таких сред имеют вид

При этом индуцированные в среде электрич. заряды наз. связанными или поляризац. зарядами с плотностью , а токи, обусловленные их изменениями,- поляризац. токами с плотностью:

Эти понятия были перенесены и на магн. поля, что можно выразить в виде системы ур-ний, аналогичной

и только потом выяснилось, что истинными источниками намагничивания среды оказались электрич. токи , а не магн. заряды. Поэтому терминология сложилась на основе физически некорректной системы

тогда как следовало бы принять беззарядовые ур-ния

что равносильно замыканию исходных M. у. (1) — (4) с помощью материальных связей

Из (6) и (7a) следует, что 2-й вариант представления материальных соотношений, в к-ром постулируются в качестве исходных векторы E и B, физически предпочтительнее.

В модели Лоренца — Максвелла усреднение микрополя Нмикро, произведённое с учётом вклада со стороны индуциров. полей, приводит к ур-ниям (9) и соответственно = В. Однако обычно параметры сред вводятся с помощью ур-ний (7), что облегчает двойственную симметризацию ф-л (подробнее см. в разделе 9). Напр., скалярные восприимчивости сред (c e , c m ) определяются соотношениями

Простейшие модели сред характеризуются пост, значениямиВ случае вакуума0.

Классификация разл. сред ооычно основывается на материальных ур-ниях типа (10) и их обобщениях. Если проницаемости e и m не зависят от полей, то M. у. (1) — (4) вместе с материальными ур-ниями (10) остаются линейными, поэтому о таких средах говорят как о линейных средах. При наличии зависимостейсреды наз. нелинейными: решения M. у. в нелинейных средах не удовлетворяют принципу суперпозиции. Если проницаемости зависят от координат то говорят о неоднородных средах, при зависимости от времени — о нестац попарных средах (иногда такие эл—динамич. системы наз. параметрическими). Для анизотропных сред скаляры e, m в (10) заменяются на тензоры: (по дважды встречающимся индексам производится суммирование). Важное значение имеют также эффекты запаздывания и нелокальности отклика среды на внеш. поля.

Значение индуциров. поляризации Р е , напр, в момент г, может определяться, вообще говоря, значениями полей во все предыдущие моменты времени, т. е.

что при преобразовании Фурье по времени приводит к зависимости [соответственноi]. Такие среды наз. средами с временной (частотной) дисперсией или просто диспергирующими средами. Аналогичная связь устанавливается и для нелокальных взаимодействий, когда отклик в точке г зависит от значения полей, строго говоря, во всех окружающих точкахно обычно всё-таки в пределах нек-рой конечной её окрестности: При преобразовании Фурье по г это приводит к появлению зависимостей такие среды наз. средами с пространственной дисперсией (см. Дисперсия пространственная).

В проводящих средах входящая в M. у. (1) — (5) плотность тока состоит из двух слагаемых: одно по-прежнему является сторонним токомобусловленным заданным перемещением электрич. зарядов под действием сторонних сил (обычно неэлектрич. происхождения), а другое — током проводимостизависящим от полей, определяемых системой M. у., и связанным с ними материальными ур-ниями вида В простейшем случае эта зависимость сводится к локальному Ома закону,

где — электропроводность (проводимость) среды. Иногда в (11) вводят обозначение, благодаря к-рому различают системы с заданными токами и системы с заданными полями (напряжениями). Для синусоидальных во времени полей, подчинённых ур-ниям (1б) — (4б) и материальным связям (10) и (11), вводится комплексная диэлектрич. проницаемость, объединяющая (10) и (11),, мнимая часть к-рой обусловлена проводимостью и определяет диссипацию энергии эл—магн. поля в среде. По аналогии вводится комплексная магн. проницаемость, мнимая часть к-рой обусловливает потери, связанные с перемагничиванием среды. Комплексные проницаемости в общем случае зависят от частоты w и волнового вектораэти зависимости не могут быть произвольными: причинности принцип связывает их действительные и мнимые части Крамерса — Кронига соотношениями.

В общем случае вид материальных ур-ний зависит также и от системы отсчёта, в к-рой эти ур-ния рассматривают. Так, если в неподвижной системе К среда характеризуется простейшими ур-ниями (10), то в инер-циальной системе К’ , движущейся относительно К с пост, скоростью и, появляется анизотропия:

где индексыобозначают продольные и поперечные ксоставляющие векторов. В рамках алгебраич. M. у. (1в) — (4в) материальные ур-ния (12) могут быть переписаны в виде

что можно трактовать как наличие временной и пространственной дисперсии. Исследование процессов с материальными связями типа (12) составляет предмет электродинамики движущихся сред. Заметим, что хотя характеристики е и m удобно симметризуют материальные ур-ния, их введение не является непременным условием замыкания M. у. Соответствующей перенормировкой допустимо свести описание магн. поля к одно-векторному, т. е. сделать но при этом даже для изотропной среды диэлектрич. проницаемость становится тензором, она различна для вихревых и потенциальных полей. Физически это связано с неоднозначностью модельного представления диполь-ных моментов, во всяком случае приони могут равноправно интерпретироваться и как зарядовые, и как токовые.

8. Граничные условия

Поскольку M. у. справедливы для любых (в рамках применимости макроэлектродинамики) неоднородных сред, то в областях резкого изменения их параметров иногда можно игнорировать тонкую структуру распределения полей в переходном слое и ограничиться «сшиванием» полей по разные стороны от него, заменяя тем самым переходный слой матем. поверхностью — границей, лишённой толщины. Если внутри переходной области имелись заряды с объёмной плотностьюили токи с объёмной плотностьюто при сжатии слоя в поверхность сохраняются их интегральные значения ·- вводятся поверхностные заряды r пов и поверхностные токи

— толщина переходного слоя.

Применение M. у. и ур-ния непрерывности приводит к следующим граничным условиям:

Здесь индексы 1 и 2 характеризуют поля по разные стороны от границы, а— единичный вектор нормали к поверхности, направленный из среды 1 в среду 2. Правила (1г) — (5г) пригодны для перехода через любые поверхности, независимо от того, совпадают ли они с границами раздела сред или проходят по однородным областям, поэтому их иногда наз. поверхностными M. у.

Иногда граничные условия (1г) — (5г) порождают краевые условия, т. е. задают не правила перехода через границу, а сами поля на ней. Напр., внутри идеального проводника в силу (11) (иначе возник бы ток неограниченной плотности), поэтому на границе раздела диэлектрик — идеальный проводник в согласии с (2г)Такие границы наз. идеальными электрич. стенками. Аналогично вводится понятие идеальной магн. стенки, на к-рой Если структура полей по одну сторону от границы универсальна, т. е. не зависит от распределения полей по др. сторону, то краевые условия могут состоять в задании не самих полей, а лишь связей между ними, напр. где Z — нек-рая скалярная или тензорная ф-ция координат границы (— тангенциальный компонент). К условиям такого рода относится, в частности, Леонтовича граничное условие для синусоидально меняющихся во времени полей на поверхности хороших проводников.

9. Двойственная симметрия Максвелла уравнений

Двойственная симметрия M. у. имеет место для любой формы их записи. Она состоит в инвариантности M. у. относительно линейных преобразований нолей, производимых по след, правилам:

Здесь— произвольный угл. параметр; в частности, при= О получаются тождественные преобразования, а при — стандартные преобразования перестановочной двойственности (операция ): замена даёт в областях, свободных от источников, новое решение M. у. При этом, однако, оно меняет местами ур-ния

и, следовательно, там, где раньше были распределены электрич. источники, возникают источники магнитные

. Поэтому с точки зрения двойственной симметрии M. у. задание материальных связей в виде представляется вполне удобным. Дуально-симметричные M. у. обладают рядом достоинств, по крайней мере в чисто методич. плане. Так, напр., они симметризуют скачки тангенциальных компонентов магн. и электрич. полей и, если задание ff Tall на поверхности идеальной электрич. стенки эквивалентно заданию поверхностного электрич. тока, то задание Я 1а „ на идеальной магн. стенке сводится к заданию магн. поверхностного тока:

Таким сведением задач с заданнымиполями к задачам с заданными токами широко пользуются в теории дифракции волн, в частности в дифракции радиоволн.

Принцип перестановочной двойственности является представителем класса дискретных преобразований (см. Симметрия ),оставляющих инвариантными M. у. Такого же сорта преобразованиями являются, в частности, операция обращения времени

последовательно осуществляемые комбинации операций

10. Максвелла уравнения в четырёхмерном представлении

Придавая времени t смысл четвёртой координаты и представляя её чисто мнимой величиной (см. Минковского пространство-время ),можно заключить описание электромагнетизма в компактную форму. Эл—магн. поле в 4-описании может быть задано двумя антисимметричными тензорами

где— Леви-Чивиты символ ,лат. индексы пробегают значения 1, 2, 3, 4, а греческие — 1, 2, 3. В 4-век-торе тока объединены обычная плотность тока j e и плотность электрич. заряда

аналогично вводят 4-вектор магн. тока.

В этих обозначениях M. у. допускают компактное 4-мерное представление:

Взаимной заменой векторов поля и индукции в ф-лах (13),(14) вводятся тензоры индукции эл—магн. поля

через к-рые также могут быть записаны M. у.:

Любая пара тензорных ур-ний, содержащая в правых частях оба 4-тока (электрич. и мат.), тождественна системе M. у. Чаще используют пару ур-ний (15 а), (18), при этом материальные ур-ния сводятся к функциональной связи между тензорами (последний чаще обозначают через.

Из антисимметрии тензоров поля, индукции и M. у. в форме (17) — (18) следует равенство нулю 4-дивергенций 4-токов:

к-рое представляет собой 4-мерную запись ур-ний непрерывности для электрич. (магн.) зарядов. T. о., 4-векторы токов являются чисто вихревыми, и соотношения (17), (18) можно рассматривать как их представление в виде 4-роторов соответствующих тензоров. Наряду с представленным здесь вариантом часто используется также 4-мерное описание, в к-ром временная координата (обычно с индексом О) берётся действительной, но 4-мерному пространству приписывается гипербодич. сигнатура в таком пространстве приходится различать ко- и контравариантные компоненты векторов и тензоров (см. Ковариантность и контравариантность).

11. Лоренц-инвариантность Максвелла уравнений

Все экспериментально регистрируемые эл—динамич. явления удовлетворяют относительности принципу .Вид M. у. сохраняется при линейных преобразованиях, оставляющих неизменным интервал и составляющих 10-мерную Пуанкаре группу: 4 трансляции, 3 пространственных (орто-) поворота и 3 пространственно-временных (орто-хроно-) поворота, иногда называемых ло-ренцевыми вращениями. Последние соответствуют перемещениям системы отсчёта вдоль осей x a с пост, скоростямиВ частности, для получается простейшая разновидность Лоренца преобразований:

, где Соответственно поля преобразуются по правилам:

Релятивистски-ковариантная запись M. у. позволяет легко находить инвариантные комбинации полей, токов и потенциалов (4-скаляров или инвариантов Лоренца группы), сохраняющихся, в частности, при переходе от одной инерциальной системы отсчёта к другой. Во-первых, это чисто полевые инварианты (см. Инварианты электромагнитного поля ).Во-вторых, это токовые (источниковые) инварианты:

В-третьих, это потенциальные инварианты:

где— магн. потенциалы (получающиеся из А е и преобразованием перестановочной двойственности), источниками к-рых являются магн. токи j m и заряды. И, наконец, многочисл. коыбиниров. инварианты типаи им подобные. Число таких комбиниров. инвариантов (квадратичных, кубичных и т. д.) по полям н источникам неограниченно.

12. Лагранжиан для электромагнитного поля

M. у. могут быть получены из наименьшего действия принципа, т. е. их можно совместить с Эйлера — Лаг-ранжа уравнениями, обеспечивающими вариационную акстремальность ф-ции действия:

здесь — лагранжиан ,являющийся релятивистски-инвариантной величиной; интегрирование ведётся по 4-мерному объёму V, (t 2 — t 1 ) с фиксиров. границами. В качестве обобщённых координат принято обычно использовать потенциалы А a и f. Поскольку лагран-жев формализм должен давать полное (замкнутое) динамич. описание системы, то при его построении нужно принимать во внимание материальные ур-ния. Они фигурируют как зависимости связанных зарядов и токов от полей В и Е·

В результате лагранжиан принимает вид инвариантной комбинации полей, потенциалов и источников:

А ур-ния Эйлера — Лагранжа для нек-рой обобщённой координаты получают приравниванием нулю соответствующих вариационных производных:

Для приходим к (4), для- к ур-нию (1) в соответствующих обозначениях. Вариационный подход позволяет придать теории универсальную форму описания, распространяемую и на описания динамики любых взаимодействий, даёт возможность получать ур-ния для комбиниров. динамич. систем, напр, электромеханических. В частности, для систем с сосредоточенными параметрами, характеризуемых конечным числом степеней свободы, соответствующие ур-ния наз. ур-ниями Лагранжа — Максвелла.

13. Единственность решений Максвелла уравнений

Различают теоремы единственности для стационарных и нестационарных процессов. Условия единственности нестационарных решений извлекаются из Пойн-тинга теоремы, где источники считаются заданными ф-циями координат и времени. Если бы они порождали два разл. поля, то разность этих полей в вакууме (или в любой линейной материальной среде) вследствие принципа суперпозиции была бы решением однородных M. у. Для обращения этой разности в нуль и, следовательно, получения единств, решения достаточно удовлетворить след, трём условиям. 1) На поверхности S, окружающей область V, где ищется поле, должны быть заданы тангенциальные составляющие поля Е тан или поля Н тан либо соотношения между ними импедансного типа: (п — нормаль к S) со значениями Z, исключающими приток энергии извне. К таковым относятся, в частности, условия излучения (см. Зоммерфельда условия излучения ),к-рым удовлетворяют волны в однородной среде на больших расстояниях от источников. Во всех случаях поток энергии для разностного поля вообще исчезает или направлен наружу (из объёма). 2) В нач. момент времени должны быть заданы все поля всюду внутри V. 3) Плотность энергии электромагнитного поля HB) должна быть положительна (вакуум, среды с . Эта частная теорема единственности обобщается на среды с нелокальными связями, а также на нек-рые виды параметрич. сред. Однако в нелинейных средах, где принцип суперпозиции не работает, никаких общих утверждений о единственности не существует.

В стационарных режимах нач. условия выпадают, и теоремы единственности формулируются непосредственно для установившихся решений. Так, в электростатике достаточно задать все источники r e ст , все полные заряды на изолиров. проводниках или их потенциалы, чтобы при соответствующих условиях на бесконечности (нужное спадание поля) решение было бы единственным. Аналогичные теоремы устанавливаются для магнитостатики и электродинамики пост, токов в проводящих средах.

Особо выделяется случай синусоидальных во времени процессов, для к-рых формулируют след, признаки, достаточные для получения единств, решения: 1) задание источников задание E тан или Н тан на ограничивающей объём V поверхности S или соответствующих импедансных условий, обеспечивающих отсутствие потока вектора Пойнтинга внутрь V; 3) наличие малого поглощения внутри V или малой утечки энергии через S для исключения существования собств. колебаний на частоте

14. Классификация приближений Максвелла уравнений

Классификация приближений M. у. обычно основывается на безразмерных параметрах, определяющих и критерии подобия для эл—магн. полей. В вакууме таким параметром является отношение , где — характерный масштаб изменения полей (либо размер области, в к-рой ищется решение), — характерный временной масштаб изменения полей.

а) а = 0 — статич. приближение, статика.

Система M. у. распадается на три.

Материальная связь в простейшем случае имеет вид . Это система M. у. для электростатики, в к-рой источниками служат заданные распределения плотности электрич. заряда и сторонней поляризации . В однородной среде эл—статич. потенциал f определяется Пуассона уравнением

Скалярное произведение векторов

Векторы

Физические законы обладают двумя свойствами, которые называют инвариантностью (или симметрией) относительно перемещений и поворотов координатных осей. Эти свойства так важны, что для учета их при изучении физических законов была разработана специальная математическая техника, называемая векторным анализом.

Важно различать физические величины двух типов. Величины первого типа характеризуются только численным значением (например, температура, количество предметов и т.д.) — это скаляры. Другие величины — векторы — характеризуются не только численным значением, но и направлением в пространстве. Численные значения физических величин и их направление в каждой точке пространства не зависят от выбора системы координат. Например, перемещение из начала координат в точку Р(х,у,z) (шаг в пространстве, который имеет определенную длину и направление).

Вектор определяется тремя числами — его проекциями на координатные оси. Например, перемещение из начала координат в точку Р(х,у,z) можно описать тремя числами х,у,z. Но можно использовать для этой цели один — единственный символ r (радиус-вектор). Радиус-вектор широко используется для задания положения точки в пространстве относительно выбранной системы координат. Символ r задается не только тремя числами х,у,z, но и числами в другой системе координат. Т.е. мы используем один и тот же символ в качестве представителя трех чисел в одной системе координат и делаем его представителем второго набора чисел, если захотим сменить систему координат. Это удобно потому, что не придется изменять форму уравнений при изменении системы координат. Очевидно, что проекции вектора при изменении системы координат должны измениться по строго определенным законам, таким же, как и тройки чисел х,у,z и . Только в этом случае, проекции вектора отображают один и тот же объект во всех системах координат. Для шага в пространстве нам очевидно, что это один и тот же объект во всех системах координат (шаг имеет определенную длину и направление в пространстве не зависящие от выбора системы координат). А бывают случаи, когда требуется специальное исследование, устанавливающее, по каким законам изменяются тройки чисел, характеризующие величину, при изменении системы координат, заранее это не очевидно. Если эти законы такие же, как и для тройки чисел х,у,z, то величине присваивается статус вектора (объекта, не зависящего от выбора системы координат).

Определим вектор математически как величину, определяемую тремя числами, которые преобразуются при изменении системы координат так же, как и координаты. То, что физические соотношения между какими-то величинами можно выразить в форме векторных уравнений отражает тот факт, что эти соотношения верны в любой системе координат.

Часто бывает удобно изобразить вектор в виде стрелки, указывающей направление. Стрелка преобразуется по тем же законам, что и шаг в пространстве. Изобразив ее, не нужно заботиться о координатных осях.

Вектор обозначается жирным шрифтом (например, r, v, a). В рукописях (конспекте и т.п.)вектор обозначается стрелкой, или черточкой над буквой.

Полезно увидеть законы преобразования хотя бы в упрощенном частном случае. Например, одна система координат повернута относительно другой вокруг оси z на угол q. Начало координат в обеих системах совпадает.

Векторная алгебра

Опишем законы, или правила, регулирующие возможные сочетания различных векторов. Прежде всего, изучим сумму двух векторов. Пусть векторы а и b задаются в какой-нибудь системе координат составляющими a_x, a_y, a_z и b_x, b_y, b_z. Предположим, что кому-то пришло в голову составить три числа a_x + b_x, a_y + b_y, a_z + b_z. Получим ли мы в результате вектор? Вектор образуют не любые три числа! Чтобы задать вектор, мы должны связать заданные нам три числа с координатной системой так, чтобы при повороте координатных осей эти числа преобразовывались по описанным ранее правилам. 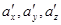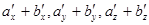Таким образом, мы должны выяснить, во что превращаются числа a_x + b_x, a_y + b_y, a_z + b_z , если известно, что при изменении системы координат числа a_x, a_y, a_z переходят в , а b_x, b_y, b_z переходят в ? Получим ли мы после поворота координатных осей числа ? Ответ, конечно, будет утвердительным потому, что уравнения для закона преобразования (1) линейны. «Складывая» векторыа и bпо только что описанному правилу, мы получим новый векторс. Мы запишем это так:

Вектор с обладает свойством:

это легко проверить, написав составляющие вектора с. Кроме того,

Векторы можно складывать в любом порядке.

Каков геометрический смысл a + b? Как будет выглядеть вектор с, если мы, скажем, изобразим a и bс помощью стрелок? Ответ на этот вопрос дает рисунок. Мы видим, что прибавить составляющие вектора b к составляющим вектора а проще всего, приложив соответствующим образом прямоугольник, определяемый составляющими b, к такому же прямоугольнику, определяемому составляющими а. Поскольку а и b хорошо подогнаны к своим прямоугольникам, то это все равно, что поставить векторb «ногами» на «голову» вектору а. Стрелка, соединяющая «ноги» вектора а и «голову» вектора b, и будет вектором с. Можно поступить иначе: поставить «ноги» а на «голову» b. Вспомнив геометрические свойства параллелограмма, можно убедиться в том, что мы снова получим тот же вектор с. Заметим, что, ставя векторы друг на друга, мы складываем их без помощи координатных осей.

Предположим, что мы умножили вектор а на число a. Что нужно понимать под таким произведением? Договоримся понимать под этим вектор с компонентами aa_x, aa_y, aa_z. Легко увидеть из законов преобразования (1), что это действительно вектор.

Рассмотрим теперь вычитание векторов. Можно определить вычитание тем же способом, что и сложение, но вместо того, чтобы складывать, будем вычитать составляющие. Можно также определить вычитание как сложение с отрицательным вектором (-b). Результат буде тот же.

Вычитание векторов показано на рисунке. На этом чертеже изображено d = a – b.

Скалярное произведение векторов

Легко понять, что длина шага в пространстве одинакова во всех координатных схемах. Следовательно, если какому-то шагу r соответствуют составляющие х,у,z в одной системе координат и составляющие в другой системе, то расстояние одно и тоже в обеих системах:

Легко доказать с помощью законов преобразования (1), что эти расстояния равны. Удобней сравнивать квадраты расстояний:

.

Незаметно мы получили новый тип величин. Мы можем построить функцию координат х,у,z, называемую скалярной функцией, — величину, которая не имеет направления, и одинакова во всех системах координат. Из вектора можно построить скаляр. Правило для этого мы уже нашли: нужно возвести в квадрат каждую из составляющих вектора и сложить их. Определим теперь новую величину, которую обозначим а×а. Это не вектор, а скаляр; это число, одинаковое во всех координатных системах и определяемое как сумма квадратов трех составляющих вектора:

(2)

Вы спросите: «В какой системе координат?» Но раз это число не зависит от системы координат, то ответ одинаков в любой системе координат. Мы имеем дело с новым видом величины, с инвариантом, или скаляром, полученным «возведением вектора в квадрат». Если теперь определить, исходя из векторов a и b, величину

(3)

то можно убедиться, что эта величина совпадает в штрихованной и нештрихованной системах координат. Чтобы доказать это, заметим, что это верно для величин а×а, b×b, c×c, где c = a + b. Мы уже знаем, что инвариантом является сумма квадратов:

Раскроем скобки в обеих сторонах этого уравнения. Перекрестные произведения дадут нам выражения типа (3), а суммы квадратов составляющих a и b – выражения типа (2). Инвариантность слагаемых типа (2) приводит к инвариантности перекрестных произведений типа (3).

Величина называется скалярным произведением двух векторов a и b и имеет много интересных и полезных свойств.

Например, легко доказать, что

Есть еще очень простой геометрический способ вычисления , при котором не надо определять составляющих векторов; просто есть произведение длин векторов a и bна косинус угла между ними. Почему? Предположим, что мы выбрали такую систему координат, в которой вектор а направлен вдоль оси х; в этом случае вектор а имеет единственную ненулевую составляющую а_х, которая равна длине вектора а. Таким образом, уравнение (3) сводится в этом случае к , что равно произведению длины вектора а на составляющую вектора b по направлению а, которая в свою очередь равна b cosq, т.е.

.

Таким образом, в этой частной системе координат мы доказали, что есть произведение длин векторов a и bна косинус угла между ними. Но если это верно в одной системе координат, то это верно и во всех системах, потому что не зависит от выбора системы координат.

Что хорошего может дать нам эта новая величина? Нужно ли физику скалярное произведение? Да, оно необходимо ему постоянно. С примерами этого мы неоднократно столкнемся. Скалярное произведение широко используется не только в физике и математике, а и во многих других науках.

Удобно определить еще одно произведение двух векторов, которое называется векторным произведением и записывается в виде . Понятие векторного произведения естественным образом появляется при анализе вращательного движения. Приведем соответствующую выдержку из раздела «Механика».

Векторное произведение

Операция с двумя векторами a и b, позволяющая получить из них новый вектор с, которая носит название «векторное произведение», обозначается обычно двумя способами:

Свойства векторного произведения

Результатом векторного произведения есть вектор, который перпендикулярен обоим перемножаемым векторам: с^а, с^b. Доказательством является равенство нулю скалярных произведений с×а и с×b (скалярные произведения можно расписать как сумму произведений одноименных проекций векторов).

Модуль векторного произведения равен произведению модулей векторов на синус угла между ними: ÷а´b ê= а b sina. Это правило легко доказывается путем вычисления результата векторного произведения через проекции векторов для простейшего частного случая: вектор а смотрит из начала координат в направлении оси х (а_y и a_z = 0; a_x = a), вектор b -расположен в плоскости ху (b_z = 0). Поскольку результат векторного произведения не зависит от выбора системы координат (это свойство любого вектора, для этого они и придуманы), правило можно распространить на произвольную систему координат.

Способ определения направления вектора, являющегося результатом векторного произведения: если вращать вектор а (первый из перемножаемых векторов) по направлению к вектору b (второй из перемножаемых векторов), то вектор c = а´b будет направлен в сторону поступательного движения, связанного с этим вращением, винта с правой резьбой. Это простая договоренность. Получается, что результатом векторного произведения является не совсем «честный» вектор. Такие вектора называются аксиальными, или псевдовекторами, в отличие от обычных полярных векторов. Аксиальные вектора хорошо передают свойства вращения.

Приводим без доказательства сводку правил векторной алгебры:

Сведения из дифференциального исчисления:

Приращение функции y(x,y,z) через малые приращения аргументов (Dх, Dу, Dz) можно вычислить по формуле:

Точность этой формулы возрастает при уменьшении приращений аргументов.

Порядок дифференцирования функции нескольких переменных не влияет на результат:

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ВЕКТОРОВ

Производные полей — градиент

Когда поля меняются со временем, то их изменение можно описать, задав их производные по t. Мы хотим также описать и их изменение в пространстве, потому что мы интересуемся связью, скажем, между температурой в некоторой точке и в точке с ней рядом. Как же задать производную температуры по координате? Дифференцировать температуру по х? Или по у, или по z?

Осмысленные физические законы не зависят от ориентации системы координат. Поэтому их нужно писать так, чтобы по обе стороны знака равенства стояли скаляры или векторы. Что же такое производная скалярного поля, скажем, ? Скаляр ли это, или вектор, или еще что? Это ни то и ни другое, потому что если взять другую ось х, то изменится. Но у нас есть три возможные производные: , , . Три сорта производных, а ведь мы знаем, что нужно как раз три числа, чтобы образовать вектор. Может быть, что три производные и представляют собой компоненты вектора:

Вектор ли это?

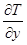
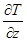
Вообще говоря, не из любых трех чисел можно составить вектор. О векторе можно говорить только тогда, когда при повороте системы координат компоненты преобразуются по правильному закону (такому же, как и тройка чисел х, у, z). Так что следует проследить, как меняются эти производные при повороте системы координат. Мы покажем, что действительно вектор. Производные действительно преобразуются при вращении системы координат так, как полагается.

В этом можно убедиться по-разному. Можно, например, задать себе вопрос, ответ на который не должен зависеть от системы координат, и попытаться выразить ответ в «инвариантной» форме. К примеру, если S = A×B и если А и В — векторы, то мы знаем, что S — скаляр (число не зависящее от выбора системы координат). Мы знаем, что S — скаляр, не проверяя, меняется ли он при изменении системы координат. Ему ничего иного не остается, раз он является скалярным произведением двух векторов. Подобным же образом, если мы знаем, что А — вектор, и у нас есть три числа В₁, В₂, В₃, и мы обнаруживаем, что

где S в любой системе координат одно и то же), то три числа В₁, В₂, В₃ обязаны быть компонентами В_х, В_у, В_z некоторого вектора В.

Рассмотрим теперь температурное поле. Возьмем две точки Р₁ и Р₂, разделенные маленьким расстоянием . Температура в Р₁ есть Т₁, а в Р₂ она равна Т₂, и их разница DТ = Т₂ — Т₁. Температура в этих реальных физических точках, конечно, не зависит от того, какие оси мы выбрали для измерения координат. В частности, DТ — тоже число, не зависящее от системы координат. Это скаляр.

Выбрав удобную систему координат, мы можем записать

где Dх, Dу, Dz — компоненты вектора (рисунок). Вспомнив формулу из дифференциального исчисления

, напишем

.

Слева стоит скаляр, а справа — сумма трех произведений каких-то чисел на Dх, Dу, Dz, которые являются компонентами вектора. Значит, три числа

тоже х-, у-, z-компоненты вектора. Мы напишем этот новый вектор при помощи символа . Символ (называемый набла) напоминает нам о дифференцировании. Читают по-разному: «набла Т», или «градиент Т», или «grad T»:

C этим обозначением формула

переписывается в более компактной форме

Или, выражая словами: разница температур в двух близких точках есть скалярное произведение градиента ÑТ на вектор DR смещения второй точки относительно первой. Последнее уравнение также служит иллюстрацией к нашему утверждению, что ÑТ — действительно вектор.

Доказательство того, что ÑТ является вектором, не зависит от того, какое скалярное поле мы дифференцируем. Все доводы остались бы в силе, если бы Т было заменено любым скалярным полем. А поскольку уравнения преобразований компонент вектора ÑТ при повороте системы координат (см. раздел Векторы) одинаковы независимо от того, что дифференцируется, то можно Т убрать и уравнение преобразования, например, х-компоненты вектора ÑТ заменить операторным уравнением:

Мы оставляем операторы «жаждущими продифференцировать что угодно».

Так как сами дифференциальные операторы преобразуются как компоненты векторного поля, то можно назвать их компонентами векторного оператора. Можно написать

или

Мы абстрагировали градиент от Т. Это одна из замечательных идей, которые украшают математику.

Необходимо все время помнить, что Ñ — это оператор. Сам по себе он ничего не означает. Вектор можно умножить на скаляр, например, на температуру Т, а произведение ÑТ — это уже не «жаждущий» оператор, его жажда утолена. Это физическая величина, имеющая смысл. Она представляет собой скорость пространственного изменения Т: х-компонента ÑТ показывает, насколько быстро Т изменяется в х-направлении. А куда направлен вектор ÑТ? Мы знаем, что скорость изменения Т в каком-то направлении — это компонента ÑТ в этом направлении (вспомним выражение DT = ÑТ×DR). Отсюда следует, что направление ÑТ обладает самой длинной проекцией; иными словами, то направление, по которому Т меняется быстрее всего. Направление градиента Т — это направление быстрейшего подъема величины Т.

Можно ли с векторным оператором Ñ производить другие алгебраические действия? Попробуем скомбинировать его с вектором. Из двух векторов можно составить скалярное произведение, например

Ñ×Е = Ñ_хЕ_х + Ñ_уЕ_у + Ñ_zE_z =

Полученная сумма инвариантна относительно преобразования координат. Если повернуть оси координат, то каждое из трех чисел, входящих в сумму изменится, однако так, что сумма останется неизменной. Итак, Ñ×Е— это скалярное поле, и оно должно представить собой некоторую физическую величину.

Скалярная величина Ñ×(Вектор) очень широко применяется в физике. Ей присвоили имя «дивергенция», или «расходимость». Например,

Можно было бы, как и для ÑТ, описать физический смысл Ñ×Е. Но мы сделаем это далее, в разделе «Интегральное исчисление векторов».

Посмотрим сначала, что можно еще извлечь из векторного оператора Ñ. Как насчет векторного произведения? Можно надеяться, что

Компоненты этого вектора можно написать, пользуясь, пользуясь обычным правилом для векторного произведения:

(Ñ´Е)_х = Ñ_уЕ_z — Ñ_zЕ_y =

(Ñ´Е)_y = Ñ_zЕ_x — Ñ_xЕ_z =

(Ñ´Е)_z = Ñ_xЕ_y — Ñ_yЕ_x =

Комбинацию Ñ´Еназывают «ротор» (пишут rot E), или (редко) «вихрь». Происхождение этого названия и физический смысл комбинации мы обсудим ниже.

В итоге мы получили три сорта комбинаций, куда входит Ñ:

Используя эти комбинации, пространственные вариации полей можно записывать в удобном виде, т.е. в виде, не зависящем от той или иной совокупности осей координат.

В качестве примера применения векторного дифференциального оператора Ñ выпишем совокупность векторных уравнений, в которой содержатся законы электромагнетизма. Их называют уравнениями Максвелла.

,

,

,

,

где r — «плотность электрического заряда» (количество заряда в единице объема), а j — «плотность электрического тока» (скорость протекания заряда сквозь единицу площади). Эти четыре уравнения содержат в себе законченную классическую теорию электромагнитного поля. Обратите внимание на простоту и элегантность записи, которая стала возможной за счет использования векторного оператора Ñ.

Вторые производные векторных полей

Из вторых производных можно составить несколько комбинаций:

(а) Ñ×(ÑТ) = Ñ 2 Т = =Скалярное поле (скалярный оператор Ñ 2 называется оператором Лапласа, или лапласианом),

Ñ(Ñ×Е)= Ñ 2 Е =Векторное поле (лапласиан действует на каждую проекцию вектора Е).

(б) Ñ´(ÑТ) = 0 (векторное произведение взаимно параллельных векторов),

(г) Ñ×(Ñ´Е) =0 (скалярное произведение взаимно перпендикулярных векторов),

Можно убедиться, что никаких иных комбинаций быть не может.

Посмотрим сперва на вторую комбинацию (б). Она имеет ту же форму, что и

потому что А ´ А всегда нуль. Значит,

Можно понять, как это получается, если расписать одну из компонент:

,

что равно нулю (вспомним уравнение из дифференциального исчисления). Это же верно и для других компонент. Стало быть, Ñ´(ÑТ) = 0 для любого распределения температур, да и для всякой скалярной функции.

Возьмем второй пример. Посмотрим, нельзя ли получить нуль другим путем. Скалярное произведение вектора на векторное произведение, содержащее этот вектор, равно нулю

потому что А´Вперпендикулярно к А и не имеет тем самым составляющих вдоль А. Сходная комбинация стоит под обозначением (г):

В справедливости этого равенства легко убедиться, проделав выкладки на компонентах.

Сформулируем без доказательства две теоремы, которые весьма полезны в физике, в частности в теории электромагнетизма.

В физических задачах часто оказывается, что ротор какой-то величины (скажем векторного поля А) равен нулю. Мы видели, что ротор градиента всегда равен нулю. Далее, может оказаться, что А будет градиентом какой-то величины, потому что тогда ротор А с необходимостью обратится в нуль. Имеется теорема, утверждающая, что если ротор А есть нуль, то тогда А непременно окажется чьим-то градиентом; существует некоторое скалярное поле y (пси), такое, что А = grad y. иными словами, справедлива

Если Ñ´А= 0, то имеется y, такое, что А= Ñy.

Сходная теорема формулируется и для случая, когда дивергенция А есть нуль. Мы видели (г), что дивергенция ротора любой величины равна всегда нулю. Если нам встретилось векторное поле D, для которого div D — нуль, то мы вправе заключить, что D — это ротор некоторого векторного поля С.

Если Ñ×D= 0, то имеется С, такое, что D= Ñ´C.

Займемся теперь комбинациями, которые не равны нулю. Возьмем комбинацию (а) Ñ×(ÑТ). В общем случае это не нуль.

,

что может, вообще говоря, быть любым числом. Это скалярное поле.

Скобок можно не ставить, а вместо этого писать:

.

Можно рассматривать Ñ 2 как новый оператор. Это скалярный оператор. Так как он в физике встречается часто, ему дали особое имя — лапласиан.

Лапласиан = .

Раз оператор лапласиана — оператор скалярный, он может действовать и на вектор. Под этим мы подразумеваем, что он применяется к каждой компоненте вектора

Последняя комбинация (д) дает векторное поле, которое может случайно возникнуть в каком-нибудь расчете. Ее можно вывести, расписывая компоненты.

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ВЕКТОРОВ

Векторные интегралы; криволинейный интеграл от Ñy

В предыдущей главе мы видели, что брать производные от поля можно по разному. Одни приводят к векторным полям, другие — к скалярным. Хотя формул было приведено довольно много, все их можно подытожить одним правилом: операторы суть три компоненты векторного оператора Ñ.

Мы уже говорили о смысле операции градиента (Ñ на скаляр). Обратимся теперь к смыслу операций вычисления дивергенции и ротора. Толкование этих величин лучше всего сделать на языке векторных интегралов и уравнений, связывающих эти интегралы. Одна из этих интегральных формул практически тривиальна, а две другие — нет. Эти формулы фактически являются математическими теоремами. Они полезны не только для толкования смысла и содержания понятий дивергенции и ротора, но и при разработке общих физических теорий. Для теории полей эти математические теоремы — все равно, что теорема о сохранении энергии для механики частиц. Подобные теоремы общего характера очень важны для более глубокого понимания физики. Кроме того, многие практические задачи мы решим, воспользовавшись этими тремя интегральными формулами.

Начнем с той интегральной формулы, куда входит градиент. Мысль, которая содержится в ней, очень проста: раз градиент есть быстрота изменения величины поля, то интеграл от этой быстроты даст нам общее изменение поля. Пусть у нас есть скалярное поле y(х, у, z). В двух произвольных точках (1) и (2) функция y имеет соответственно значения y(1) и y(2). [Используется такое удобное обозначение: (2) означает точку (х₂, у₂, z₂), а y(2) — это то же самое, что y(х₂, у₂, z₂).] Если Г (гамма) — произвольная кривая, соединяющая (1) и (2) (рисунок), то справедлива

Интеграл, стоящий здесь, — это криволинейный интеграл от (1) до (2) вдоль кривой Г от скалярного произведения вектора Ñy на другой вектор, ds, являющийся бесконечно малым элементом дуги кривой Г [направленной от (1) к (2)].

Разность значений скалярного поля в двух точках равна криволинейному интегралу от касательной составляющей градиента этого скаляра вдоль любой кривой, соединяющей первую точку со второй.

Поток векторного поля

Прежде чем рассматривать следующую интегральную теорему — теорему о дивергенции, — необходимо разобраться в одной идее, смысл которой в случае, например, потока тепла легко усваивается. Определим вектор h плотности потока тепла (вместо слова «тепла» можно подставить — заряда, жидкости, энергии электромагнитного поля и т.д. — чего угодно) как количество тепла, протекающего сквозь единицу площади, перпендикулярной направлению потока тепла, в единицу времени. Направление вектора h совпадает с направлением потока тепла в данной точке пространства. Положим, что внутри тела имеется замкнутая поверхность S, ограничивающая объем V (рисунок). Нам хочется узнать, сколько тепла вытекает из этого объема. Мы это можем, конечно, определить, рассчитав общий тепловой поток через поверхность S.

Обозначим через da площадь элемента поверхности. Этот символ заменяет двумерный дифференциал. Если, например, элемент окажется в плоскости ху, то

Позже мы будем иметь дело с интегралами по объему, и тогда будет удобно рассматривать элемент объема в виде малого кубика и обозначать его dV, подразумевая, что

Поток тепла через элемент поверхности da равен произведению площади на составляющую h, перпендикулярную к da. Введем единичный вектор n, определяющий направление нормали к элементу поверхности da (рисунок). Искомая составляющая h равна

и тогда поток тепла сквозь da равен

А весь поток тепла через произвольную поверхность получается суммированием вкладов от всех элементов поверхности. Иными словами предыдущее выражение интегрируется по всей поверхности

Поток тепла сквозь S (из объема V) .

Этот интеграл мы будем называть «поток h через поверхность». Мы рассматриваем h как «плотность потока» тепла, а поверхностный интеграл от h — это общий поток тепла наружу через поверхность, т.е. тепловая энергия за единицу времени (джоули в секунду).

Мы хотим эту идею обобщить на случай, когда вектор не представляет собой потока какой-то величины, а, скажем, является электрическим полем. Конечно, если это будет нужно, то и в этом случае все равно можно проинтегрировать нормальную составляющую электрического поля по площади. Хотя теперь она уже не будет ничьим потоком, мы все еще будем употреблять слово «поток». Мы будем говорить, что

Поток Е сквозь поверхность S .

Слову «поток» мы придаем смысл «поверхностного интеграла от нормальной составляющей» некоторого вектора. То же определение будет применяться и тогда, когда поверхность незамкнута.

А возвращаясь к частному случаю потока тепла, обратим внимание на те случаи, когда количество тепла сохраняется. Представим себе, к примеру, материал, в котором после первоначального подогрева не происходит ни дальнейшего подвода, ни поглощения тепла. Тогда, если из какой-то замкнутой поверхности наружу поступает тепло, содержание тепла во внутреннем объеме должно падать. Так что в условиях, когда количество тепла сохраняется, мы говорим, что

, где Q — запас тепла внутри S.

Это толкование возможно оттого, что речь идет о потоке тепла, и оттого, что мы предположили, что количество тепла сохраняется. Конечно, если бы внутри объема создавалось тепло, нельзя было бы говорить о полном запасе тепла в нем.

Укажем теперь на интересное свойство потока любого вектора. Можем при этом представлять себе вектор потока тепла, но верно это будет и для произвольного векторного поля С. Представим себе замкнутую поверхность S, окружающую объем V. Разобьем теперь объем на две части каким-то «сечением» (рисунок). Объем V₁ окружен поверхностью S₁, составленной частью из прежней поверхности S_а и частью из «сечения» S_аb. Объем V₂ окружен поверхностью S₂, составленной частью из прежней поверхности S_b и замкнутой сечением S_аb. Поток через поверхность S равен сумме потоков через поверхность S₁ и S₂. Действительно:

Поток сквозь S₁ =

Поток сквозь S₂ =

Заметим, что во втором интеграле мы обозначили внешнюю нормаль к S_аb буквой n₁, если она относится к S₁, и буквой n₂, если она относится к S₂ (рисунок). Ясно, что n₁ = — n₂, и тем самым

Складывая теперь уравнения для потоков сквозь S₁ и S₂, мы убеждаемся, что сумма потоков как раз равна сумме двух интегралов, которые, взятые вместе, дают поток через первоначальную поверхность S = S_a + S_b.

Мы видим, что поток через всю внешнюю поверхность S можно рассматривать как сумму потоков из тех двух частей, на которые разрезан объем. Эти части можно еще разрезать: скажем, V₁ разбить пополам. Опять придется прибегнуть к тем же доводам. Так что для любого способа разбиения первоначального объема всегда остается справедливым то свойство, что поток через внешнюю поверхность (первоначальный интеграл) равен сумме потоков изо всех внутренних частей.

Приведем без доказательства теорему, доказывающую, что дивергенция произвольного вектора в какой-то точке пространства равна потоку этого вектора, приходящемуся на единицу объема (объемной плотности потока в данной точке пространства). Таким образом, дифференциальная характеристика векторного поля — дивергенция, связана с интегральной характеристикой — способностью векторного поля формировать поток.

Поверхностный интеграл от нормальной составляющей произвольного вектора по замкнутой поверхности S (поток вектора через замкнутую поверхность S) равен интегралу от дивергенции вектора по объему V, лежащему внутри этой поверхности:

Объемный интеграл суммирует потоки из всех бесконечно малых частей объема V (вспомним, что поток из объема равен сумме потоков из всех частей этого объема) и дает, тем самым, общий поток через поверхность S, ограничивающую объем V.

Циркуляция векторного поля

Рассмотрим ротор поля примерно так же, как рассматривали дивергенцию. Связь дивергенции с интегралом по поверхности (потоком векторного поля), которая следует из теоремы Остроградского Гаусса заранее вовсе не очевидна. Эта связь является предметом доказательствав данной теореме. Столь же неочевидной является связь ротора с другой характеристикой поля — циркуляцией. Рассмотрим теорему Стокса, которая описывает эту связь. Вначале рассмотрим понятие циркуляции векторного поля.

Если С — произвольное векторное поле, мы возьмем его составляющую вдоль кривой линии и проинтегрируем эту составляющую по замкнутому контуру. Интеграл называется циркуляцией векторного поля по контуру.

Пусть Г — произвольный замкнутый контур в пространстве (воображаемый, разумеется). Пример мы видим на рисунке. Криволинейный интеграл от касательной составляющей С по контуру записывается в виде

Заметим, что интеграл берется по всему замкнутому пути, а не от одной точки до другой. Кружочек на знаке интеграла должен нам напоминать об этом. Такой интеграл называется циркуляцией векторного поля по кривой Г. Название связано с тем, что первоначально так рассчитывали циркуляцию жидкости. Но название это, как и поток, было распространено на любые поля, даже такие, в которых «циркулировать» нечему.

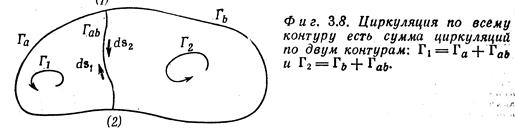
По аналогии с потоком можно доказать, что циркуляция вдоль контура есть сумма циркуляций вдоль двух меньших контуров. Положим, что, соединив две точки (1) и (2) первоначальной кривой с помощью некоторой линии, мы разбили кривую на два контура Г₁ и Г₂ (рисунок).

Контур Г₁ состоит из Г_а — части первоначальной кривой слева от (1) и (2) и «границы» Г_ab. Контур Г₂ состоит из остатка первоначальной кривой плюс та же граница.

Циркуляция вдоль Г₁ есть сумма интеграла вдоль Г_а и вдоль Г_ab. Точно так же и циркуляция вдоль Г₂ есть сумма двух частей, одной вдоль Г_b, другой — вдоль Г_ab. Интеграл вдоль Г_ab для кривой Г₂ имеет знак, противоположный тому знаку, который он имел для кривой Г₁, потому что направление обхода противоположны (в обоих криволинейных интегралах направления поворота нужно брать одни и те же).

Повторяя прежние аргументы, мы можем убедиться, что сумма двух циркуляций даст как раз криволинейный интеграл вдоль кривой Г. Интегралы по Г_ab сократятся. Циркуляция по одной части плюс циркуляция вдоль другой равняется циркуляции вдоль внешней линии. Этот процесс разрезания большого контура на меньшие можно продолжить. При сложении циркуляций по меньшим контурам смежные части будут сокращаться, так что сумма сведется к циркуляции вдоль единственного первоначального контура.

Теперь предположим, что первоначальный контур — это граница некоторой поверхности. Существует бесконечное множество поверхностей, границей которых служит все тот же первоначальный замкнутый контур. Наши результаты не зависят, однако, от выбора этих поверхностей. Сперва мы разобьем наш первоначальный контур на множество малых контуров, лежащих на выбранной поверхности (рисунок). Какой бы ни была форма поверхности, циркуляция по Г есть сумма циркуляций по всем маленьким контурам.

Криволинейный интеграл от касательной составляющей произвольного вектора по замкнутому контуру Г (циркуляция вектора по замкнутому контуру Г) равен поверхностному интегралу от нормальной составляющей ротора этого вектора по произвольной поверхности S, ограниченной этим контуром:

Теорему следует дополнить соглашением о знаках. Как вообще узнавать, какое направление надо выбирать для положительного направления «нормальной» компоненты вектора Ñ´С? «Положительную» нормаль надо связывать с направлением обхода вдоль контура пользуясь правилом правого винта. При таком условии знаки левой и правой части выражения в теореме Стокса совпадают.

Получается, что нормальная к элементу поверхности компонента ротора произвольного вектора равна поверхностной плотности циркуляции этого вектора в точках данного элемента поверхности. Такова связь ротора с циркуляцией векторного поля.

дивергенцияхарактеризует способность векторного поля формировать поток. Она равна объемной плотности потока векторного поля. Поток вектора из какой-то заданной области пространства есть сумма потоков из бесконечно малых объемов, на которые можно разделить эту область пространства, то есть интеграл по объему от дивергенции вектора.

ротор —вектор,характеризующий способность векторного поля формировать циркуляцию. Проекция ротора на направление нормали к поверхности равна поверхностной плотности циркуляции векторного поля. Циркуляция вектора вдоль какого-то замкнутого контура равна сумме циркуляций вдоль бесконечно малых участочков произвольной поверхности, которую ограничивает контур, то есть интегралу по этой поверхности от нормальной составляющей ротора.

Подытожим самые существенные моменты из математики векторных полей.

, ,

можно рассматривать как три составляющие векторного оператора Ñ; формулы, следующие из векторной алгебры, остаются правильными, если этот оператор считать вектором

2. Разность значений скалярного поля в двух точках равна криволинейному интегралу от касательной составляющей градиента этого скаляра вдоль любой кривой, соединяющей первую точку со второй:

3. Поверхностный интеграл от нормальной составляющей произвольного вектора по замкнутой поверхности равен интегралу от дивергенции вектора по объему, лежащему внутри этой поверхности:

4. Криволинейный интеграл от касательной составляющей произвольного вектора по замкнутому контуру равен поверхностному интегралу от нормальной составляющей ротора этого вектора по произвольной поверхности, ограниченной этим контуром

Роль псевдовекторов в математическом моделировании формального аналога электромагнитного поля Текст научной статьи по специальности « Электротехника, электронная техника, информационные технологии»

Аннотация научной статьи по электротехнике, электронной технике, информационным технологиям, автор научной работы — Попов Игорь Павлович

Показано, что классическая модель магнитного поля допускает нарушение третьего закона Ньютона , исключает взаимодействие соосных элементов проводников с токами, не предусматривает существование моментов сил , действующих на элементы проводников, законом Ампера принято считать формулу, в общем случае несовместимую с его основным результатом. С привлечением таких математических объектов, как псевдовекторы , комбинированные и сопряженные векторы построена формальная модель аналога электромагнитного поля, не имеющая указанных особенностей, в частности, формальные аналоги закона электромагнитной индукции являются простым следствием других свойств и соотношений поля, при этом построенная модель удовлетворяет основному требованию Ампера безусловному выполнению третьего закона Ньютона .

Похожие темы научных работ по электротехнике, электронной технике, информационным технологиям , автор научной работы — Попов Игорь Павлович

THE ROLE OF PSEUDOVECTORS IN FORMAL ELECTROMAGNETIC FIELD ANALOGY MATHEMATICAL MODELING

It is shown that the classical model of the magnetic fi eld allows the violation of Newton’s third law, eliminates the interference of coaxial conductors elements with currents, does not provide for the existence of the forces’ momentum acting on the elements of the conductors, Ampere’s law is considered to be a formula which in the general case is incompatible with its main result. With the use of such mathematical entities as pseudovectors, combined and associated vectors we have constructed a formal model of the electromagnetic fi eld analog, not having these features, for instance, the formal analogy of the law of electromagnetic induction is a simple consequence of other properties and relations of fi elds. With all these factors considered, the developed model meets the essential Ampere’s requirements the unconditional implementation of Newton’s third law.

Текст научной работы на тему «Роль псевдовекторов в математическом моделировании формального аналога электромагнитного поля»

РОЛЬ ПСЕВДОВЕКТОРОВ В МАТЕМАТИЧЕСКОМ МОДЕЛИРОВАНИИ ФОРМАЛЬНОГО АНАЛОГА ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

Показано, что классическая модель магнитного поля допускает нарушение третьего закона Ньютона, исключает взаимодействие соосных элементов проводников с токами, не предусматривает существование моментов сил, действующих на элементы проводников, законом Ампера принято считать формулу, в общем случае несовместимую с его основным результатом. С привлечением таких математических объектов, как псевдовекторы, комбинированные и сопряженные векторы построена формальная модель аналога электромагнитного поля, не имеющая указанных особенностей, в частности, формальные аналоги закона электромагнитной индукции являются простым следствием других свойств и соотношений поля, при этом построенная модель удовлетворяет основному требованию Ампера — безусловному выполнению третьего закона Ньютона.

Ключевые слова: псевдовектор, магнитное поле, третий закон Ньютона, соос-ные элементы проводников, моменты сил, напряженность, индукция, дивергенция.

В классической теории магнитного поля пондеромоторные силы взаимодействия между замкнутыми контурами с токами удовлетворяют третьему закону Ньютона (ТЗН). Однако эти силы являются результатом сложения элементарных сил, действующих между малыми элементами проводников с токами, для которых ТЗН может нарушаться [1]. На рис. 1 представлен предельный случай такого нарушения.

Рис. 1. Нарушение ТЗН

Первый элемент проводника dl1 с током 11 действует на второй с силой

dF2l = ¡2 [ Л2, Щ ] = -^Г |>2,[ 4,г]], (!)

где dB1 — магнитная индукция, д— магнитная проницаемость, г — радиус-вектор.

Эта сила имеет максимальное значение, поскольку все перемножаемые векторы взаимно перпендикулярны. В то же время, второй элемент действует на первый с силой

М12 = /1Ц, ЙВ2 ] = [^11,[^12,г]] = 0

так как й12 и г коллинеарны.

Известны попытки согласования электродинамики с ТЗН [2, 3]. Однако эти работы представляются излишне феноменологическими.

Модель магнитного поля имеет ряд других противоречий, которые будут показаны ниже.

Целью настоящей работы является не исправление существующей теории электромагнитного поля, а построение в К3 модели формального аналога электромагнитного поля, с одной стороны — максимально похожей на электромагнитное поле, с другой стороны — не вступающей в противоречие с ТЗН — одним из основных законов механики и свободной от других противоречий модели магнитного поля. На невозможность нарушения ТЗН при взаимодействии проводников с токами указывал Ампер [4, 5].

Далее величины формального аналога электромагнитного поля для отличия их от соответствующих величин электромагнитного поля обозначаются другим шрифтом: q, I, В, Н, D, Е, F ^ q, I, В, Н, й, Е, Г.

В качестве одной из предпосылок дальнейшего рассмотрения может быть предложена измененная конфигурация вышеприведенного примера, в которой второй проводник расположен параллельно первому. ТЗН в этом случае не нарушается. При этом

1. Первый признак формального аналога электромагнитного поля, совпадающий с соответствующим признаком магнитного поля

Этот признак состоит в том, что если элементы формальных аналогов токов

11Й11 и 12й12 лежат в одной плоскости и перпендикулярны соединяющему их радиус-вектору г, то так же как и в (2) они взаимодействуют с силой

й Р,2 =- й Р21 =- т-1 1 2 2 12

Здесь m — формальный аналог магнитной проницаемости.

Если S1 и S2 — плоскости, образованные соответственно парами векторов /1dl1, r и /2 dl 2, r, и a — угол между S1 и S2, то

(/1dl1 )s 1 (/2 dl2 )s 2

dF = -mK 1 l’n V2 2’n cos a . (3)

2. Второе противоречие модели магнитного поля

Несмотря на то, что Ампер считал, что силы взаимодействия соосных токов существуют (этот вывод он сделал, в том числе, и на основании собственных много-

численных экспериментов), в классической модели магнитного поля соосные проводники с токами не взаимодействуют.

Из того обстоятельства, что сила взаимодействия элементов проводников с токами является градиентом энергии магнитного поля, созданного этими элементами, следует, что между элементами со стабилизированными токами существует сила взаимодействия, если при изменении расстояния между ними энергия результирующего поля, созданного элементами, изменяется [6]. Впредь, для того, чтобы не усложнять рассуждения учетом влияния электромагнитной индукции, имеется в виду, что рассматриваемые токи являются стабилизированными.

Если соосные проводники с токами не взаимодействуют, то для них должно выполняться тождество

где А — работа, Ж — энергия суммарного поля обоих проводников. Это легко проверить.

При условии с^ = С12 = С1, I = -I и г = да.

где Н — напряженность поля одного проводника.

При г = 0 Ж0 = 0 и Ж0 — ф 0 . Это означает, что коллинеарные проводники с токами взаимодействуют с силой

В этой связи возникает необходимость выяснить, в какой мере эксперименты, выполненные Био и Саваром, исключают возможность существования этой силы.

Эти эксперименты, по существу, не являлись опытами по определению напряженности магнитного поля. Это и не были эксперименты по определению взаимодействия линейных проводников с током. Они задумывались и осуществлялись для определения силы взаимодействия проводников и постоянного магнита. Не случайно

в формулу входила «магнитная масса» т (Г = тМкту/г2 [7]). А поскольку действие магнита определяется действием круговых токов, которые можно условно заменить одним эквивалентным круговым током, то эксперименты по существу показывали, как отрезок линейного проводника взаимодействует с круговым током.

Пусть магнит располагается на оси линейного проводника (но не самом проводнике) так, чтобы ось совпадала с плоскостью кругового тока магнита. Круговой ток можно представить в виде двух токов, направленных в противоположные стороны и соосных линейному проводнику. Один из этих токов в соответствии с (4) притягивается к линейному проводнику, а второй с такой же по величине силой отталкивается от него и суммарное осевое усилие равно нулю. По этой причине эксперименты Био и Савара не могли выявить силу взаимодействия соосных проводников и, следовательно, не дают никаких оснований ее «запретить».

Таким образом, вторым противоречием классической модели магнитного поля является противоречие с методом определения силы как градиента энергии, т.е. отсутствие учета силового взаимодействия между соосными составляющими элементов проводников с токами.

Модель формального аналога электромагнитного поля свободна от указанного противоречия.

Замечание. Нетрудно убедиться, что ТЗН нарушается тогда, когда векторы & имеют продольные составляющие, коллинеарные радиус-вектору. Из этого следует вывод: если исходить из того, что ТЗН нарушаться не может в силу своей всеобщности (по крайней мере, в условиях магнитостатики), значит, при классическом расчете из-за двойного векторного произведения (1) теряются силы взаимодействия продольных проводников или их составляющих. На существование этих сил указывал Ампер и их наличие обосновано выше.

Поскольку расчет сил методом двойного векторного произведения корректен лишь в случае, когда перемножаемые векторы ортогональны, следует прибегать к более универсальному методу определения сил как градиента энергии (4).

3. Второй признак формального аналога электромагнитного поля, не совпадающий с соответствующим противоречивым признаком магнитного поля

Этот признак заключается в том, что соосные элементы формальных аналогов

токов /1&1 и /2 & 2 взаимодействуют с силой

где kx — некоторый безразмерный коэффициент, величина которого будет установлена ниже. В классической модели магнитного взаимодействия эта сила считается равной нулю.

4. Общий случай взаимного расположения элементов формальных аналогов токов

В общем случае взаимодействующие элементы формальных аналогов токов

/1dl1 и I2dl 2 расположены под углом у относительно друг друга и составляют с соединяющим их радиус-вектором r углы ф1 и ф В соответствии с теоремой косинусов для сторон сферического треугольника [8] можно показать:

cosy = sin91sin92cosa + cos91cos92. (6)

Векторы Ijdlj и I2dl2 можно разложить на поперечные (I1dl1)n , (I2dl2)n и

продольные (Ijdlj )т , (I2dl2)т составляющие относительно радиус-вектора. В соответствии с (3), (5) и (6) суммарная сила взаимодействия элементов формальных аналогов токов I1dl1 и I2 dl 2 равна

(LdL)sl(L dl2)s 2 , (I,dl,). (I2 dl2)T

d f = -mK 1 1 nK 2 2’n cos a — kT mK 1 1tV 2 2’T = 4%r2 4%r2

8Ш Ф1 )(/2Л2 8Ш Ф2) к (к^К 008 Ф1)(/2Ш2 008 ф2 )

4 п г2 /1ё11/2 Л2 4пг2

(8Ш Ф1 8Ш Ф2 008 а + к 008 ф1 008 ф2 ) =

[008 у + (кг — 1) 008 Ф1 008 Ф2 ] .

аГ направлена вдоль г.

Выражение (7) совпадает с основной формулой Ампера применительно к магнитному взаимодействию [4]. По-видимому, является недоразумением считать законом Ампера выражение (1), которое в общем случае несовместимо с его основным результатом.

При этом Ампер полагал к = — 0,5. Однако эта величина нуждается в уточнении. Для ее определения потребуется прояснить ситуацию с моментами.

5. Моменты сил в классическом магнитном поле и заимствование результатов для формального аналога электромагнитного поля

Если в системе из п контуров с токами какой-то контур под действием поля

повернется на угол а Ф, то энергия магнитного поля изменится на величину Ыё ф и совершится механическая работа Ыё Ф, где М — момент, действующий по направлению а Ф [9]. Для к-го контура уравнение по второму закону Кирхгофа:

При умножении уравнения на ¡к&

¡кЯкЛ + 1кс№к = екгкЛ

Для всей совокупности контуров

Это энергия, полученная от источников электродвижущей силы за вычетом тепла. В соответствии с законом сохранения энергии

В частном случае, если при повороте контура на угол d ф токи во всех контурах меняются таким образом, чтобы потокосцеиления оставались неизменными, т. е.

сЯ>к = 0. M = -dWu/dф. Представляет интерес другой частный случай со стабилизированными токами

(ik = const), для которых

При подстановке в (8)

к=1 L к=1 _ игг м

Таким образом, получены следующие результаты:

5.1. В обоих рассмотренных частных случаях приращение энергии магнитного

поля 0Жи равно механической работе Mdф .

5.2. В первом частном случае работа совершается за счет изменения энергии

5.3. Во втором частном случае и работа и изменение энергии осуществляются за счет энергии внешних источников.

5.4. На объекты (10!), испытывающие воздействие со стороны магнитного поля, действуют моменты, если энергия совокупного магнитного поля является функцией углов (одной из сторон которых является оИ).

5.5. Для определения моментов нужно аналитические выражения для энергии магнитного поля продифференцировать по углам, функции которых входят в состав этих выражений.

5.6. В первом частном случае поле стремится повернуть взаимодействующий с ним объект таким образом, чтобы энергия поля убывала.

5.7. В случае стабилизированных токов поле стремится повернуть взаимодействующий с ним объект таким образом, чтобы энергия поля возрастала.

Для описания формального аналога электромагнитного поля заимствуются результаты по п.п. 5.4, 5.5, 5.7., а именно:

5.8. На элементы формальных аналогов токов ¡0\, испытывающие воздействие со стороны поля, действуют моменты, если энергия совокупного поля является функцией углов (одной из сторон которых является ¡0\).

5.9. Для определения моментов нужно аналитические выражения для энергии формального аналога электромагнитного поля продифференцировать по углам, функции которых входят в состав этих выражений.

5.10. В случае стабилизированных формальных аналогов токов поле стремится повернуть взаимодействующий с ним элемент ¡0\ таким образом, чтобы энергия поля возрастала.

Вестник Псковского государственного университета 6. Уточнение величины к

В соответствии с (7) энергия формального аналога электромагнитного поля равна

= m / 1 1. В соответствии с 5.10. поле стремится повернуть элементы таким образом, чтобы энергия поля возросла. А это значит, что моменты М и М направлены в одну сторону, в сторону уменьшения ф1 и ф2 и принцип противодействия нарушается. Таким образом, предположение k > 1 неверно.

Пусть k Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Определение 1. Псевдовектор — это скаляр, в котором содержится информация о включенном в него векторе.

Определение 2. Комбинированный вектор — это произведение вектора и псевдовектора.

Обозначение комбинированного вектора:

Нижний индекс содержит информацию о направлении вектора, верхний индекс — информацию о направлении псевдовектора.

С учетом введенных понятий напряженность для формального аналога электромагнитного поля можно представить в виде:

Величина напряженности для формального аналога электромагнитного поля, созданного элементом формального аналога тока /Л, не зависит от угла между радиус-вектором г и /Л.

9. Третье и четвертое противоречия классической модели магнитного поля

В описаниях силовых полей, созданных ранее классической модели магнитного поля, — гравитационного и электростатического — напряженность определяется как сила, действующая на единичный объект, порождающий поле. Соответственно этому направление вектора напряженности естественным образом совпадает с направлением вектора силы. В классической модели магнитного поля вектор напряженности ортогонален вектору силы. В модели формального аналога электромагнитного поля это противоречие устранено.

У гравитационного и электростатического полей напряженность зависит от свойств среды. При этом в описании электростатического поля индукция от свойств

среды не зависит [11]. В классической модели магнитного поля все наоборот [12]. В этом заключается его четвертое противоречие с традиционной моделью поля. Нет причины переносить это противоречие на модель формального аналога электромагнитного поля.

10. Индукция и потенциал для формального аналога электромагнитного

Индукция для формального аналога электромагнитного поля

о = М! I = -_!_ >Г. (14)

г 4пг2 1 Ог 4пг3 ^ ‘

Формальный аналог электромагнитного поля имеет радиальный характер, следовательно, оно является потенциальным. При 01 ^ 0 эквипотенциальными поверхностями являются сферы. Для такого поля в соответствии с [1, 9]

где ф — потенциал поля.

Если выбрать систему координат таким образом, чтобы ось абсцисс совпала с радиус-вектором, то

11. Свойства мнимых и комбинированных векторов и операции с ними

11.4. При взаимодействии мнимых векторов на них распространяются все правила операций с векторами.

11.5. Мнимый вектор и вектор взаимодействуют между собой как скаляр и вектор.

11.6. При взаимодействии комбинированных векторов между собой могут использоваться двойные записи операций: « <•>•», « <х>-», « <х>— », « <х>х », « <х>+ »,

« <х>+ », « <•>+ », « <•>+ », « <+>•». Операция в скобках связывает мнимые векторы. Вторая операция связывает векторы. При перемножении псевдовектора и комбинированного вектора нет необходимости размещения знака произведения в скобки. Очевидно, что знак произведения «•» или «X » в этом случае распространяется на псевдовекторные составляющие.

Вестник Псковского государственного университета

11.7. При необходимости скобки раскрываются применением двойных скобок,

11.8. В присутствии вектора u скобка раскрываться не может. Исключение составляет случай, когда выражение, стоящее в скобке, является скаляром, например, в результате скалярного произведения векторов. Например,

11.9. pUp! <->+ q«4!=

U<> + — = <Р• q>íU + -] = pqcos(p, q)fU + .

u V | u V J | u V J

11.10. В отсутствии вектора u скобка не раскрывается, если другая часть равенства является скалярной величиной.

Ipu lpV l pl u VJ l p

11.12. e« + bUq>= e jp 1U + 6 Ы U = U = с U = ^ .

l pu l qu u l p qu l сu

11.13. e,íp! • 6» = e jp 1U• 6 jq| = eb j> • I1U = e6f£• Я1U = сU = c .

pu l ql p qu 11.13.1.

=

= p • q

11.14. еГ хЬ^ — е]£I£хЬД 1 = еЬ]£хМ £ = С .

11.16. М-ыЛ^ +дру-— ^ +дру-+^ = V • £.

I дх дУ дzдх ду дz

12. Связь между величинами формального аналога электромагнитного поля

й^12 — й• — -—гГ• <12й12>— -т1 1 1 2з 2/г — -т 1 1 2з 2 Г12, (15)

4 пг3 4 пг3 4 пг

что совпадает с (11). Полученное выражение существенно отличается от (1), которое

принято называть законом Ампера.

х/2ей2>(г _]т¡А ы е ] 4 пг3 (ГГ)Г_ 4 п г 11’*2 (16)

что сов падает с (12)

м _Ф- _— < /1ег1>• < /2 2>+ с _ — ^’12 е 2 + с,

что совпадает с (10).

13. Теорема Гаусса для формального аналога электромагнитного поля

Поскольку формальный аналог электромагнитного поля имеет радиальный характер, для него выполняется теорема Гаусса

где X — площадь замкнутой поверхности, ограничивающей некоторый объем, 1см — формальный аналог тока смещения. В дифференциальной форме

где ] — формальный аналог плотности тока, дО/д! — формальный аналог плотности тока смещения, Б — формальный аналог электрического смещения или электрической индукции.

Скобки могут быть раскрыты двойными скобками (11.7)

Еще одним противоречием классической модели магнитного поля является равенство нулю его дивергенции.

Непрекращающиеся попытки отыскания в рамках классической теории магнитного заряда и магнитного монополя равносильны попыткам опровержения известного математического тождества

Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

12.2. Векторное деление двух векторов.

Определение. Частное e^b от векторного деления вектора e на вектор b есть вектор

q = e*b = ex — = ex-= —-(exb) = —r =—sin 0 (iQ)

b b • b b2У ‘ b2 bd •

(e * b)(b — e) = -sin20,

12.3. Теоремы о полном делении векторов.

12.3.1. Если известны частные от скалярного p и векторного q деления двух векторов e и b, а также делитель b, то делимое определяется, как

bp + b x q = 1 [b (e • b) + b x( e x b)] = ^ [b (e • b) + e (b • b)- b (b • e )] = e.

12.3.2. Если известны частные от скалярного p и векторного q деления двух

векторов e и b, а также делимое e, то делитель определяется, как

^^ = ± bV [(e • b) e + (e x b)x e] = ± [(e • b) e + b (e • e)-e (e • b )] = b.

15. Формальный аналог индуцированного электрического поля

Формальный аналог напряженности электрического поля — это сила, действующая на единичный формальный аналог электрического заряда д. Пусть последний движется со скоростью V. Могут быть рассмотрены следующие частные случаи. 1. Продольное движение (рис. 2).

Рис. 2. Продольное движение

Серия «Естественные и физико-математические науки». 8/2016 В соответствии с (15) формальный аналог напряженности электрического поля

m ,, „ , i ч m ,, „ , midi midi idlт /dlт

4 пг 3 ^ » 1 ‘ 4 пг 3 ^ % ‘ 4 пг3 4 пг2 I dl % I

В скалярной форме

Формальный аналог ЭДС

с1Е = d Ет dl = d Н 2. Поперечное движение (рис. 3).

Рис. 3. Поперечное движение

В соответствии с (16)

С другой стороны

В соответствии с (19)

d E n = ^ = _L d m * r = • r > * r = • r > x \ = d q d q r

4nr3 ^ v » v » ‘ r2 4nr3 ^ n ‘ rA 4nr

— ir-v ^ n )=-mvidi n=-dH-v w,. (21)

В скалярной форме

Формальный аналог ЭДС

dE = d Е dl = ^ Н vdl.

16. Изменяющееся поле

Для точки, расположенной в конце радиус-вектора г, изменение величины 1^1

равносильно перемещению вектора 1^1 вдоль радиус-вектора г с некоторой скоростью. Это дает возможность использовать результаты предыдущего раздела.

1. Продольное (относительно ¡С1) поле. На рис. 2 заряд удаляется от источника поля, поэтому оно уменьшается. Если заряд неподвижен, то для уменьшения поля источник должен двигаться со скоростью, имеющей противоположный знак. С учетом этого и в соответствии с (20)

СЕт=- СН т V ¡^ = — СН т *

2. Поперечное (относительно ¡С1) поле. В соответствии с (21)

В произвольной точке поле можно разложить на продольную и поперечную со-