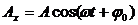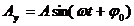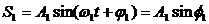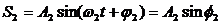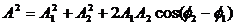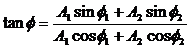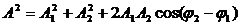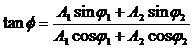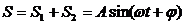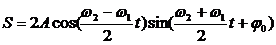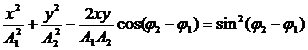Складываются два взаимно перпендикулярных колебания выражаемых уравнениями

Складываются два взаимно перпендикулярных колебания, выражаемых уравнениями x = 2 sin пt, y = cos п(t + 0,5) (длина в сантиметрах, время в секундах).

Готовое решение: Заказ №8366

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Физика

Дата выполнения: 21.08.2020

Цена: 209 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

№2 053. Складываются два взаимно перпендикулярных колебания, выражаемых уравнениями x = 2 sin пt, y = cos п(t + 0,5) (длина в сантиметрах, время в секундах). Найти уравнение траектории и построить её на чертеже, показав направление движения точки.

Преобразуем выражение для координаты у: . То есть: . Это и есть уравнение траектории точки. Поскольку синус принимает значения от -1 до 1, то точка будет двигаться по отрезку прямой от точки (0; 0) к точке А(2; -1); затем в обратную сторону к точке В(-2; 1); затем снова к точке А и т. д. Изобразим траекторию точки.

• Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемым уравнениями: x = A1 cos w1t и y = A2 cos w2(t + t), где A1 = 4 см, w1 = п с-1, A2 = 8 см, w2 = п с-1, t = 1 с. Найти уравнение траектории и начертить её с соблюдением масштаба.
• Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемым уравнениями: x = A1 cos wt и y = A2 cos w(t + t), где A1 = 4 см, A2 = 8 см, w = п с-1, t = 1 с. Написать уравнение траектории точки и построить график её движения.
• Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями x = A coswt, y = B coswt, где A = 2 см, B = 3 см. Найти уравнение траектории точки и построить траекторию с соблюдением масштаба. Указать направление движения точки и пояснить свой ответ.
• Точка одновременно участвует в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями: x = sinпt (мм) и y = cosп(t + 0,5) (мм). Найти уравнение траектории точки y(x). Изобразить траекторию.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Сложение колебаний

Тело, совершающее колебания, способно принимать участие в нескольких колебательных процессах одновременно. В таком случае возникает необходимость выяснить, каким будет результирующее колебание.

Сложение колебаний направленных по одной прямой

Рассмотрим сложение двух гармонических колебаний одинакового направления и равной частоты. Тогда смещение ($x$) совершающего колебания тела будет равно сумме смещений $x_1$ и $x_2$, которые представим в виде уравнений:

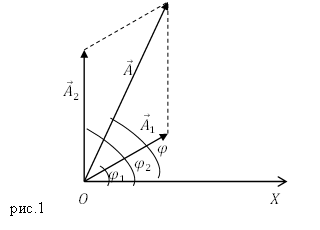
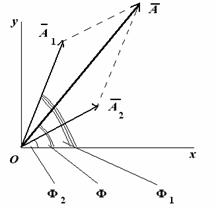
Колебания (1) и (2) представим на векторной диаграмме в виде векторов $<\overline>_1$ и $<\overline>_2$ (рис.1).

Из рис.1 видно, что амплитуду результирующего колебания можно найти как:

где $A_1$; $A_2$ — амплитуды сложенных колебаний; $<\varphi >_2;;<\varphi >_1$ — начальные фазы суммирующихся колебаний. При этом начальную фазу полученного колебания ($\varphi $) вычисляют, применяя формулу:

Из выражения (4) видно, что если $<\varphi >_2-<\varphi >_1=0$, тогда получим колебание, амплитуда которого равна:

При разности фаз равной $<\varphi >_2-<\varphi >_1=\pm \pi $, что означает, что колебания находятся в противофазе, амплитуда сложенных колебания составляет:

Суперпозиция взаимно перпендикулярных колебаний

Пусть у нас происходят два взаимно перпендикулярные гармонические колебания с одной частотой $<\omega >_0$. Колебания происходят вдоль осей X и Y. Пусть начало отсчета времени было таким, что начальная фаза первого колебания равнялась нулю. При этом уравнения колебаний предстанут в виде:

Уравнения (8) и (9) вместе представляют уравнение траектории движения точки в параметрическом виде. Исключаем время из уравнений, получаем уравнение траектории:

Уравнение траектории точки, которая принимает участие в перпендикулярных колебаниях с амплитудами $A_1$и $A_2$ и начальными фазами $<\varphi >_2и<\varphi >_1$:

Уравнение (10) — это уравнение эллипса.

В случае равенства начальных фаз составляющих колебаний уравнение траектории преобразуется к виду:

что говорит о движении точки по прямой линии. Точка, совершающая гармонические колебания движется по этой прямой, расстояние от начала координат до точки равно:

Если $\Delta \varphi =<\varphi >_2-<\varphi >_1=\frac<\pi ><2>,$ уравнением траектории становится выражение:

что означает, траектория движения эллипс.

Если частоты нормальных друг другу колебаний отличны на очень небольшую величину $\Delta \omega $, то их рассматривают как колебания с равными частотами, но переменной разностью фаз. При этом суммарное движение проходит по медленно изменяющей вид кривой.

Траектории движений суперпозиций взаимно нормальных колебаний с разными частотами представляют собой сложные кривые, которые называют фигурами Лиссажу.

Примеры задач на сложение колебаний

Задание. Какова разность фаз суммируемых колебаний, если складывались два колебания, направленных по одной прямой, обладающих одинаковыми амплитудами и периодами? Сложились они в колебание той же амплитуды.

Решение. В качестве основы для решения задачи используем выражение для вычисления амплитуды складывающихся колебаний, если они направлены вдоль одной прямой:

Учитывая условия задачи выражение (1.1) преобразуем к виду:

Выразим из (1.2) искомую разность фаз:

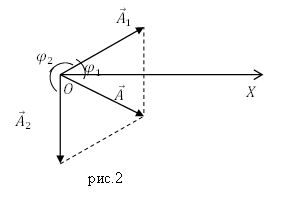
Изобразим векторную диаграмму колебаний (рис.2).

Ответ. $\Delta \varphi =\frac<4\pi ><3>или\frac<2\pi ><3>$

Задание. Материальная точка совершает одновременно два взаимно перпендикулярных колебания: $x=A<\cos \left(<\omega >_0t\right)\ >,y=B<\cos \left(<\omega >_0t\right)\ >,$ каким будет уравнение траектории движения точки?

Решение. Из уравнения:

Подставим правую часть выражения (2.2) вместо $<\cos \left(<\omega >_0t\right)\ >$ в формулу:

Уравнением движения точки будет прямая линия.

Ответ. $y=\fracx$

Сложение гармонических колебаний

Если колебательная система одновременно участвует в двух (или более) независимых колебательных движениях, возникает задача — найти результирующее колебание. В случае однонаправленных колебаний под этим понимается нахождение уравнения результирующего колебания; в случае взаимно перпендикулярных колебаний — нахождение траектории результирующего колебания.

Метод векторных диаграмм

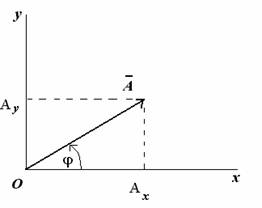
Рассмотрим вращающийся против часовой стрелки с постоянной угловой скоростью w вектор А. Очевидно, что угол j = w t + j₀ где j₀ — начальный угол.

Проекции вектора А на оси координат запишутся:

Видно, что проекции вращающегося вектора на оси координат по форме совпадают с уравнением гармонических колебаний, если угловой скорости вектора сопоставить угловую частоту колебаний, а начальному углу — начальную фазу.

Проводя аналогию дальше, можно сказать, что результат сложения двух однонаправленных колебаний можно получить следующим путем: необходимо сложить два вектора, а проекции суммарного вектора на оси координат будут являться уравнениями результирующего колебания. Рассмотрим этот метод на примере сложения двух колебаний с произвольными частотами. Пусть наше тело участвует в двух совпадающих по направлению колебаниях:

Сопоставим этим колебаниям два вектора А₁ и А₂, вращающихся с соответствующими угловыми скоростями.

Сопоставляем колебаниям проекции векторов на ось y. Задача сложения колебаний сводится к нахождению проекции вектора А на ось y (амплитуда результирующего колебания) и угла f (фаза результирующего колебания).

Из очевидных геометрических соображений находим:

Отметим, что в общем случае сложения колебаний с разными частотами амплитуда результирующего колебания будет зависеть от времени. Если же частоты одинаковы, то 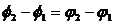, то есть зависимость от времени исчезает. На языке векторной диаграммы это означает, что складываемые векторы при своем вращении не меняют своего относительного положения. В этом случае формулы для амплитуды и фазы результирующего колебания запишутся так:

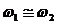
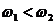
Рассмотрим сложение двух однонаправленных колебаний с неравными, но близкими частотами, то есть , и пусть для определенности . Для простоты пусть начальные фазы и амплитуды этих колебаний равны. В результате сложения двух колебаний

получим уравнение суммарного колебания:

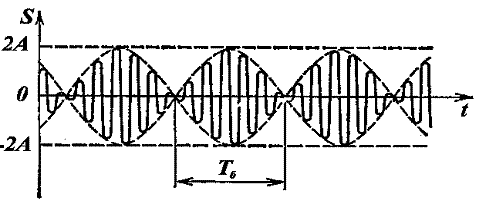
Полученное результирующее колебание не является гармоническим (сравни с уравнением (1)); такого вида колебания носят название биений, название понятно, если посмотреть на график колебаний.

Величина, стоящая перед синусом, меняется со временем относительно медленно, так как разность частот мала. Эту величину условно называют амплитудой биений, а разность складываемых частот 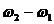— частотой биений (циклической).

При сложении взаимно перпендикулярных колебаний необходимо найти уравнение траектории тела, то есть из уравнений колебаний типа x = x(t), y = y(t) исключить t и получить зависимость типа y(x).

например, сложим два колебания с одинаковыми частотами:

исключив время, получим:

В общем случае это — уравнение эллипса. При A₁=A₂ — окружность, при 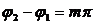(m — целое) — отрезок прямой.

Вид траектории при сложении взаимно перпендикулярных колебаний зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Получающиеся кривые носят название фигур Лиссажу.