Сколько уравнений статики в пространстве

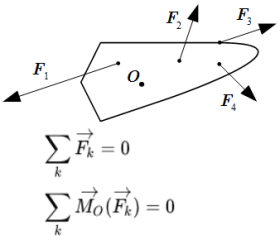
Методика решения задач статики в пространстве.

Решение задач статики в пространстве выполняется в следующей последовательности:

1. Составляется расчётная схема конструкции.

2. Определяются проекции всех сил на координатные оси х,у,z.

3. Составляются уравнения равновесия.

4. Из уравнений равновесия вычисляются реакции связей.

Основная литература: 1;2

Дополнительная литература: 1;3

1. Назовите порядок решения задач статики в пространстве.

2. Сколько уравнений равновесия нужно составить для пространственной системы сходящихся сил?

3. Сколько уравнений равновесия нужно составить для пространственной системы произвольно расположенных сил?

Лекция №11,12.

Цели занятия:Рассмотреть явление трения.

План занятия:

1. Основные понятия о трении.

2. Трение скольжения.

3. Трение качения.

Трение.

Основные понятия о трении.

Трение – это явление сопротивления относительному перемещению, возникающего между двумя телами в зонах соприкосновения поверхностей этих тел.

Существуют следующие виды трения.

1. Трение покоя – это трение двух тел, когда тела не перемещаются относительно друг друга.

2. Трение движения – это трение двух тел, находящихся в относительном движении.

Трение движения бывает следующих видов:

a). Трение скольжения.

b). Трение качения.

c). Трения качения с проскальзыванием.

Трение скольжения.

Трение скольжения – это трение движения, при котором скорости соприкасающихся тел в точках касания различны.

Трение скольжения характеризуется силой трения.

Сила трения – это сила сопротивления относительному перемещению двух тел при трении.

Рассмотрим тело, лежащее на горизонтальной шероховатой плоскости. Сила тяжести G уравновешивается реакцией плоскости N. Если к телу приложить небольшую силу F, то оно не придёт в движение, т. к. эта сила будет уравновешиваться силой трения F_ТР, которая направлена вдоль плоскости. Если постепенно увеличивать силу F, то до определённого её значения тело будет оставаться в покое; при дальнейшем увеличении силы F тело придёт в движение.

Отсюда видно, что сила трения в состоянии покоя в зависимости от силы F может изменяться от нуля до какого – то максимального значения. Максимальное значения сила трения имеет в момент начала движения. Сила трения всегда направлена в сторону, противоположную направлению относительного движения тела.

Сформулированы три основных закона трения скольжения:

1. Сила трения не зависит от величины площади трущихся поверхностей.

2. Максимальная сила трения прямо пропорциональна реакции плоскости.

3. Сила трения зависит от материала тел, состояния трущихся поверхностей, наличия и рода смазки.

f – коэффициент трения скольжения (определяется по справочнику).

Некоторые значения коэффициента трения скольжения:

Сталь по стали без смазки: f = 0,15…0,3

Сталь по стали со смазкой: f = 0,1…0,18

Дерево по дереву без смазки: f = 0,4…0,6

Сталь по льду: f = 0,02

Резина по асфальту: f ˃ 1

Трение качения.

Трение качения – это трение движения, при котором скорости соприкасающихся тел в точках касания одинаковы по величине и направлению.

Если движение двух соприкасающихся тел происходит при одновременном качении и скольжении, то в этом случае возникает трение качения с проскальзыванием.

При трении качения возникает момент трения М_ТР, который в состоянии покоя может изменяться от нуля до какого – то максимального значения, причём максимальным он будет в момент начала движения.

Трение качения характеризуется коэффициентом трения качения, который обозначается буквой к и определяется по справочнику.

Некоторые значения коэффициента трения качения для катка по плоскости:

Мягкая сталь по мягкой стали: к = 0,005 см

Закалённая сталь по закалённой стали: к = 0,001 см

Чугун по чугуну: к = 0,005 см

Дерево по стали: к = 0,03…0,04 см

Дерево по дереву: к = 0,05…0,08 см

Резиновая шина по шоссе: к = 0,24 см

Момент трения вычисляется по формуле

Трение качения меньше трения скольжения, поэтому в технике лучше применять не трение скольжения, а трение качения, например, вместо подшипников скольжения лучше применять подшипники качения.

Основная литература: 1;2

Дополнительная литература: 1;3

1. Что такое трение?

2. Какие существуют виды трения?

3. Чем характеризуется трение скольжения?

4. Сформулируйте законы трения скольжения.

5. Чем характеризуется трение качения?

Лекция №13.

Цели занятия:

1. Рассмотреть понятие центра тяжести.

2. Рассмотреть определение положения центра тяжести.

План занятия:

1. Центр тяжести.

2. Методы определения центра тяжести.

3. Определение положения центра тяжести для некоторых простых фигур.

Центр тяжести.

Центр тяжести тела – это точка тела, в которой приложена сила тяжести.

Некоторые пути нахождения центра тяжести:

1. Если однородное тело имеет ось симметрии, то центр тяжести тела лежит на этой оси.

2. Если однородное тело имеет две оси симметрии, то центр тяжести находится в точке их пересечения.

3. Центр тяжести однородного тела вращения лежит на оси вращения.

Для сложных фигур положение центра тяжести вычисляется в следующей последовательности:

1. Проводятся вспомогательные оси х,у.

2. Сложная фигура разделяется на несколько простых.

3. Определяются площади простых фигур и площадь всей сложной фигуры.

4. Определяется положение центра тяжести всех простых фигур и вычисляются координаты этих центров тяжести относительно вспомогательных осей х,у.

5. Вычисляются координаты центра тяжести сложной фигуры относительно вспомогательных осей х,у по формулам:

Статика – раздел теоретической механики

Определение и роль статики в теоретической механике

Основной задачей статики является установление законов преобразования системы сил в эквивалентные системы. Методы статики применяются не только при изучении тел, находящихся в равновесии, но и в динамике твердого тела, при преобразовании сил в более простые эквивалентные системы.

Под состоянием равновесия, в статике, понимается состояние, при котором все части механической системы покоятся относительно некоторой инерциальной системы координат. Одним из базовых объектов статики являются силы и точки их приложения.

Понятие силы

Единицей измерения силы является один Ньютон:
.
В технике широко используется килоньютон:
.

Как следует из определения, сила – это векторная величина, которая, в трехмерном пространстве, имеет три проекции на оси координат. Также задать силу можно с помощью абсолютной величины (модуля) и направления. Для материальной точки, сила приложена к самой точке. Но если мы рассматриваем твердое тело, то кроме вектора силы нам нужно еще указать и точку ее приложения. Таким образом, действие силы на твердое тело характеризуется вектором силы и точкой ее приложения. Если выбрать систему отсчета, то действие силы на твердое тело определяется двумя векторами. Это вектор силы, и вектор, проведенный из начала системы отсчета в точку приложения силы.

Система сил, действующих на тело – это совокупность векторов сил, приложенных к телу, и точек их приложения.
Эквивалентные системы сил Две системы сил являются эквивалентными, если законы движения любых точек твердого тела совпадают при действии любой из этих систем.
Эквивалентное преобразование системы сил – это переход от одной системы сил к эквивалентной ей системе.
Система взаимно уравновешивающихся сил – это система сил, не меняющая уравнений движения или уравнений равновесия твердого тела. То есть это система, эквивалентная отсутствию сил.
Равнодействующая – это одна сила, действие которой эквивалентно действию данной системы сил.

Закрепленные, скользящие и свободные векторы

Поскольку действие силы на твердое тело определяется двумя векторами, то часто под силой подразумевают множество, состоящее из двух векторов – вектора силы, и вектора точки ее приложения относительно выбранной системы координат. Такие множества подразделяются на три класса, для которых вводят специальные термины.

Закрепленный вектор – это множество, состоящее из образующего вектора и точки его приложения. Два закрепленных вектора считаются равными только в том случае, если равны их образующие векторы и совпадают точки приложения. Закрепленный вектор также называют связанным или фиксированным вектором.
Скользящий вектор – это множество, состоящее из образующего вектора и точки его приложения, обладающее тем свойством, что точку приложения можно перемещать вдоль прямой, параллельно образующему вектору. То есть два скользящих вектора считаются равными, если равны образующие векторы и точки их приложения расположены на одной прямой, параллельной образующему вектору.
Свободный вектор – это множество, состоящее из образующего вектора и точки его приложения. Два свободных вектора считаются равными, если равны образующие векторы, не зависимо от точек приложения.
Линия действия силы – это прямая, проведенная через точку приложения силы параллельно ее направлению.

Если мы рассматриваем упругое тело, то сила – это закрепленный вектор. Деформации зависят не только от величин и направлений сил, но и от точек их приложения. Если мы рассматриваем движение или равновесие абсолютно твердого тела, то действующая сила является скользящим вектором. Перемещение ее точки приложения вдоль линии ее действия не меняет уравнений движения или уравнений равновесия. Угловая скорость вращения абсолютно твердого тела является свободным вектором. Она характеризует движение в целом, и ее значение одинаково во всех точках тела.

С математической точки зрения, статика – это алгебра скользящих векторов.

Проекции силы на оси координат

Сила в трехмерном пространстве

Пусть у нас есть декартова система координат Oxyz . И пусть – единичные векторы, направленные вдоль ее осей , и , соответственно. Пусть – проекции вектора силы на оси координат. Тогда разложение силы на составляющие вдоль координатных осей имеет вид:
.
Абсолютное значение (модуль) силы:
.

Введем единичный вектор , направленный вдоль вектора силы . Тогда
.
Эта формула выражает тот факт, что вектор силы можно задать, указав ее модуль F и направление . Вектор имеет три проекции на оси координат: . Поскольку его длина равна единице: , то они связаны соотношением:
.
То есть единичный вектор имеет только две независимые компоненты. Таким образом, для задания вектора силы нужно знать три величины:
либо три проекции на оси координат ;
либо модуль F и направление , которое задается двумя независимыми величинами.

Введем углы между вектором силы и осями координат , и . Тогда проекции силы на оси координат определяются по формулам:
;
.
Косинусы углов называются направляющими косинусами.

Направляющие косинусы вектора – это косинусы углов между вектором и осями координат. Они являются проекциями единичного вектора , сонаправленного с :
,
и связаны соотношением:
.

Сила на плоскости

Результаты, приведенные выше, можно применить и для плоской декартовой системы координат Oxy . В этом случае имеем:
;
;
;
;
;
;
.
Поскольку , то . Последнее уравнение представляет собой известную тригонометрическую формулу:
.
Для задания вектора силы , необходимо знать две независимые величины:
либо проекции вектора на оси координат ;
либо модуль F и направление , которое задается одним углом .

Аксиомы статики

Часть аксиом являются основными законами механики. Другая часть относится к законам преобразования сил, действующих на абсолютно твердое тело, и применяется только к задачам теоретической механики. По своей сути, они выражают собой тот факт, что действие силы на тело является скользящим вектором.

1. Аксиома инерции (закон инерции Галилея)
Существуют такие системы отсчета, в которых любая материальная точка, не взаимодействующая с другими телами и точками, движется прямолинейно и равномерно. В частности, если тело покоилось в определенный момент времени, то оно будет покоиться и в последующие моменты.

Такие системы отсчета называются инерциальными. В механике, если это особо не оговорено, под системой отсчета подразумевается именно инерциальная система отсчета. Аксиому инерции иногда формулируют так.

1′. Аксиома инерции
В инерциальной системе отсчета, под действием взаимно уравновешивающихся сил, материальная точка находится в состоянии покоя или движется прямолинейно и равномерно, а первоначально покоившееся тело продолжает покоиться и в последующие моменты времени.

2. Аксиома равновесия двух сил
Две силы, приложенные к абсолютно твердому телу, являются уравновешенными тогда и только тогда, когда они равны по модулю, направлены в противоположные стороны и их линии действия совпадают.

3. Аксиома присоединения и исключения уравновешивающихся сил
Кинематическое состояние твердого тела не изменится, если к действующей на него системе сил прибавить или отнять уравновешенную систему сил.

То есть, прибавляя или исключая уравновешенную систему сил, мы получаем эквивалентную систему сил.

Следствие аксиом 2 и 3
Действие силы на твердое тело не изменится, если точку приложения силы перенести вдоль ее линии действия. То есть сила, приложенная к твердому телу, является скользящим вектором. Доказательство

4. Аксиома параллелограмма сил
Две силы, приложенные к телу в одной точке, можно заменить их равнодействующей силой, равной векторной сумме этих сил и приложенной к той же точке.
Верно и обратное. Любую силу можно разложить на две (и более) силы по правилу векторной суммы (по правилу параллелограмма), приложенных в той же точке, что и исходная сила.

То есть, если силы и приложены в одной точке, то их можно заменить равнодействующей , приложенной к той же точке. Сумму векторов можно найти двумя способами.
1) Можно вычислить проекции сил на оси прямоугольной системы координат:
.

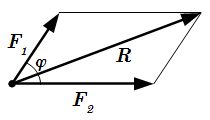
Сложение сил по правилу параллелограмма

2) Можно сложить векторы по правилу параллелограмма (см. рисунок).
;
.
Здесь – угол между векторами и . Точкой обозначено скалярное произведение векторов.

5. Аксиома равенства действия и противодействия (3-й закон Ньютона)
Всякому действию соответствует равное и противоположно направленное противодействие.

То есть если мы возьмем все силы, действующие на тело 2 со стороны тела 1, и объединим их с силами, действующими на тело 1 со стороны тела 2, то получим уравновешенную систему сил.

6. Принцип отвердевания
Если деформируемое тело находится в равновесии, то его равновесие не нарушится, если тело считать абсолютно твердым.

Система сходящихся сил

Система сходящихся сил всегда имеет равнодействующую , равную векторной сумме этих сил:
,
и приложена в точке их пересечения.

Таким образом, проекции равнодействующей системы сходящихся сил на координатные оси равны алгебраическим суммам проекций этих сил на оси координат:
;
.

Условия равновесия системы сходящихся сил
Если тело или система тел, на которые действует сходящаяся система сил, находится в покое, то равнодействующая этих сил равна нулю:
.
Это дает три уравнения равновесия:
.

Теорема о трех непараллельных силах
Если твердое тело находится в равновесии под действием трех сил, линии действия двух из которых пересекаются в одной точке, то все силы лежат в одной плоскости и являются сходящимися.

Следствие
Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то эти силы являются сходящимися.

Параллельные силы

Ранее мы отмечали, что система сходящихся сил имеет равнодействующую. То есть такую систему можно заменить одной силой. Приведем еще важные примеры систем сил, имеющих равнодействующую.

Две силы одного направления

Пусть мы имеем две однонаправленные параллельные силы и . Переместим точки их приложения вдоль линий их действия в точки A и B так, чтобы отрезок AB был перпендикулярен силам. Тогда система сил и имеют равнодействующую , приложенную в точке C . Направление равнодействующей совпадает с направлениями и . Абсолютная величина равна сумме сил:
.
Точка приложения C находится между A и B и делит отрезок AB обратно пропорционально модулям сил:
.

Две противоположно направленные силы

Теперь рассмотрим противоположно направленные силы и , различающиеся по величине, . Пусть . Эта система также имеет равнодействующую , направление которой совпадает с направлением большей по модулю силы, а абсолютное значение равно абсолютному значению разности модулей сил:
.
Точка приложения C равнодействующей находится на продолжении отрезка AB , ближе к наибольшей по модулю силе . Расстояния до точек A и B также обратно пропорциональны и :
.

Момент силы относительно точки

Определение

Абсолютное значение момента силы относительно точки O равно произведению силы на плечо этой силы относительно выбранной точки O . Направление момента перпендикулярно плоскости, проходящей через точку O и линию действия силы.
Доказательство

Геометрическая интерпретация

Пусть векторы и расположены в плоскости рисунка. Согласно свойству векторного произведения, вектор перпендикулярен векторам и , то есть перпендикулярен плоскости рисунка. Его направление определяется правилом правого винта. На рисунке вектор момента направлен на нас. Пусть α – угол между векторами и . Абсолютное значение момента:
.

Из точки O проведем перпендикуляр OH к линии действия силы . Из прямоугольника OAH имеем: . Тогда
.
То есть абсолютное значение момента силы относительно точки O равно произведению силы F на плечо |OH| этой силы относительно точки O .

Компоненты момента силы в декартовой системе координат

Выберем декартову систему координат Oxyz с началом в точке O . Найдем компоненты вектора момента силы в этой системе координат относительно ее начала.

.
Здесь – единичные векторы в направлении осей ; – координаты точки A в выбранной системе координат: .

Таким образом, момент силы имеет следующие компоненты:
(М.1) ;
(М.2) ;
(М.3) .
Компоненты представляют собой значения момента силы относительно осей , соответственно.

Свойства момента силы относительно центра

Момент относительно центра O , от силы, проходящей через этот центр, равен нулю.
Доказательство

Если точку приложения силы переместить вдоль линии, проходящей через вектор силы, то момент, при таком перемещении, не изменится.
Доказательство

Момент от векторной суммы сил, приложенных к одной точке тела, равен векторной сумме моментов от каждой из сил, приложенных к этой же точке:
.
Доказательство

То же самое относится и к силам, чьи линии продолжения пересекаются в одной точке.

Если векторная сумма сил равна нулю:
,
то сумма моментов от этих сил не зависит от положения центра, относительно которого вычисляются моменты:
.
Доказательство

Теорема Вариньона о моменте равнодействующей
Если данная система сил имеет равнодействующую, то момент равнодействующей относительно любой точки равен векторной сумме моментов сил системы относительно той же точки.

Пара сил

Из предыдущих формул ⇑ видно, что если противоположно направленные силы имеют равные модули: , то система сил не имеет равнодействующей. Действительно, в этом случае . Пытаясь использовать предыдущие формулы, мы получим деление на нуль. Такую систему сил называют парой сил.

Пара сил – это система из двух сил , равных по абсолютной величине, имеющих противоположные направления, приложенных к разным точкам тела и не лежащих на одной прямой.
Плечо пары сил – это кратчайшее расстояние h между линиями действия сил, входящих в пару.
Момент пары сил – это векторная сумма моментов сил, входящих в пару, вычисленная относительно любой точки. Абсолютное значение момента пары равно произведению силы на плечо пары:
.

Теорема о независимости выбора центра при вычислении момента пары
Векторная сумма моментов сил, составляющих пару, не зависит от выбора точки, относительно которой вычисляются моменты.
Теорема об эквивалентности пар
Две пары, имеющие равные векторы моментов, эквивалентны. То есть у пары можно менять модуль силы и длину плеча, оставляя неизменным ее момент.
Теорема о возможности перемещения пары
Пару сил можно переносить в любом направлении. Другими словами, если пару сил переместить параллельным переносом в любое положение, то она будет эквивалентна исходной паре.
Теорема о сложении нескольких пар
Система нескольких пар сил эквивалентна одной паре, вектор момента которой равен векторной сумме моментов исходных пар.
Условие равновесия пар
Система, состоящая только из нескольких пар, является уравновешенной, если векторная сумма моментов пар равна нулю:
.

Момент силы относительно оси

Часто встречаются случаи, когда нам нужно знать не все компоненты момента силы относительно выбранной точки, а только проекцию момента на выбранное направление.

Момент силы относительно оси, проходящей через точку O – это проекция вектора момента силы относительно точки O , на направление оси.

Свойства момента силы относительно оси

Момент относительно оси от силы, линия действия которой проходит через эту ось, равен нулю.
Доказательство

Момент относительно оси от силы, параллельной этой оси равен нулю.
Доказательство

Вычисление момента силы относительно оси

Пусть на тело, в точке A действует сила . Найдем момент этой силы относительно оси O′O′′ .

Построим прямоугольную систему координат. Направим ось z вдоль O′O′′ . Из точки A опустим перпендикуляр AO на O′O′′ . Через точки O и A проводим ось Ox . Перпендикулярно Ox и Oz проводим ось Oy . Разложим силу на составляющие вдоль осей системы координат:
.
Сила пересекает ось O′O′′ . Поэтому ее момент равен нулю. Сила параллельна оси O′O′′ . Поэтому ее момент также равен нулю. По формуле (М.3) находим:
.

Заметим, что компонента направлена по касательной к окружности, центром которой является точка O . Направление вектора определяется правилом правого винта.

Условия равновесия

Главный вектор и главный момент

Подчеркнем, что величина главного момента зависит от выбора центра, относительно которого вычисляются моменты.

Пространственная система сил

Основная форма условий равновесия

Условия равновесия системы сил
Для того, чтобы твердое тело под действием произвольной системы сил находилось в равновесии, необходимо и достаточно, чтобы главный вектор и главный момент, относительно произвольной точки C , равнялись нулю:
;
.
Здесь – точка приложения силы , .
Доказательство

Это основная форма условий равновесия. Точка C может, как принадлежать телу, так и находится за его пределами. Обычно центр C выбирают так, чтобы сделать вычисления более простыми. Спроектировав каждое из этих векторных уравнений на три направления, получим шесть уравнений, из которых можно определить шесть неизвестных величин.

Вторая форма условий равновесия

Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма моментов внешних сил, действующих на тело, относительно произвольным образом выбранных точек и равнялась нулю, и чтобы сумма проекций сил на произвольное направление, не перпендикулярное направлению , равнялась нулю:
;
;
.
Доказательство

Третья форма условий равновесия

Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма моментов внешних сил, действующих на тело, относительно произвольным образом выбранных точек и , не лежащих на одной прямой, равнялась нулю:
;
;
;
.
Доказательство

Плоская система сил

Все изложенное для пространственной системы сил является применимым и для плоской системы. Направим оси x и y декартовой системы координат в плоскости действия сил, а ось z – перпендикулярно. Тогда z компоненты координат точек и сил равны нулю: . Также равны нулю x, y компоненты моментов сил относительно произвольной точки C : . То есть момент может иметь отличное от нуля значение только для z компоненты. Поскольку z компонента не входит в плоскую систему координат xy , то, в двумерном пространстве, момент силы уже не является вектором, а является скаляром (точнее псевдоскаляром). Его называют алгебраическим моментом силы относительно центра C (или просто моментом силы относительно центра C ), и обозначают символом с маленькой буквы без знака вектора:
.

Величина является моментом силы относительно оси, проходящей через точку C перпендикулярно плоскости действия сил. Момент вычисляют как произведение модуля силы на плечо со знаком плюс или минус:
.
Если, при неподвижном центре C , сила стремится повернуть систему против часовой стрелки, то момент положителен . В противном случае – отрицательный: .

Величину момента от силы , приложенной в точке A , относительно центра C , также можно выразить через компоненты векторов по формуле:
,
где и – координаты точек A и C , соответственно.

Условия равновесия плоского тела

Для плоской системы сил можно составить три уравнения, из которых можно определить три неизвестных величины. Считаем, что сила приложена в точке .

Основная форма условий равновесия
;
;
.

Вторая форма условий равновесия
;
;
.

Третья форма условий равновесия
;
;
;
.

Связи и их реакции

Определения и свойства

Принцип освобождаемости
Всякое несвободное тело можно рассматривать как свободное, если действие связей заменить их реакциями, приложенными к телу.

Основные типы связей и их реакции

Плоские и пространственные задачи

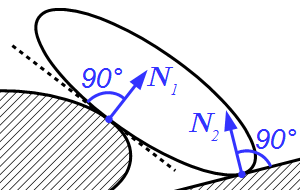
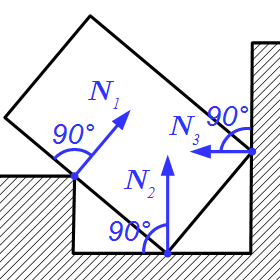
Две гладкие не острые поверхности. Через точку соприкосновения проводим касательную плоскость к этим поверхностям. Реакция является силой, направленной перпендикулярно этой плоскости, то есть, направлена по нормали к обеим поверхностям в точке их соприкосновения.

Одна из гладких поверхностей является острием. Реакция является силой, направленной вдоль нормали не острой поверхности в точке соприкосновения.

Две шероховатые поверхности. То же самое, что и для гладких поверхностей, только в точке соприкосновения добавляем силу трения, лежащую в плоскости касания.

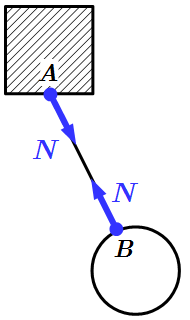
Невесомая нить и стержень. Реакция направлена вдоль нити или стержня. При этом на нить всегда действует сила растяжения. На стержень может действовать как растягивающая, так и сжимающая сила.

Плоские задачи

Следующие связи применяют только в плоских задачах.

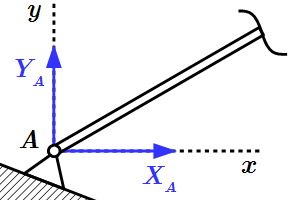
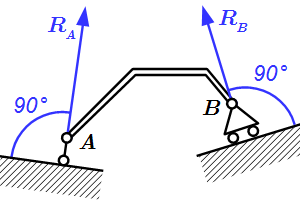
Неподвижный шарнир. Реакция является силой, проходящей через ось шарнира. Обычно ее раскладывают на две составляющие параллельно осям координат.

Подвижный шарнир, или опора на катках. Реакция является силой, которая проходит через ось шарнира перпендикулярно опорной поверхности.

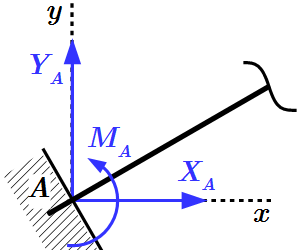
Заделка. Реакция состоит из силы, проходящей через точку соединения и момента относительно оси, проходящей через точку соединения перпендикулярно плоскости фигуры. Силу обычно раскладывают на две составляющие параллельно осям координат.

Пространственные задачи

Цилиндрический шарнир или петля. Реакция является силой, проходящей через ось шарнира, перпендикулярно направлению оси. Обычно ее раскладывают на две составляющие параллельно осям координат.

Сферический подшипник или подпятник. Реакция является силой, проходящей через центр подшипника. Обычно ее раскладывают на три составляющие параллельно осям координат.

Заделка. Реакция состоит из силы, проходящей через точку соединения и момента относительно этой точки. Силу и момент обычно раскладывают на три составляющие параллельно осям координат.

Силы трения

Трение скольжения

Рассмотрим тело, которое скользит по поверхности другого тела с отличной от нуля скоростью v под действием внешней силы . Если поверхности абсолютно гладкие, то в точках соприкосновения тел возникает только сила давления N , перпендикулярная плоскости соприкосновения тел. Для шероховатых поверхностей, возникает еще сила трения , параллельная плоскости соприкосновения, направленная в сторону, противоположную скорости движения. Величина силы трения пропорциональна силе давления и не зависит от площади соприкосновения поверхностей:
(Т1) .
Здесь f – безразмерный коэффициент, который называется динамическим коэффициентом трения, или коэффициентом трения скольжения. Он зависит от материалов и обработки соприкасаемых поверхностей и почти не зависит от скорости относительного движения. При расчетах его считают постоянной.

Сила трения скольжения – это сила трения, приложенная к точкам соприкосновения движущихся тел и параллельная плоскости их соприкосновения. То есть это сила, препятствующая скольжению одного тела по поверхности другого. При расчетах, под силой трения скольжения понимают равнодействующую всех сил трения, возникающих в точках соприкосновения тел.

Закон Амонта – Кулона
Сила трения скольжения направлена параллельно плоскости соприкосновения тел в сторону, противоположную их движению, которое возникло бы при отсутствии трения. Она не зависит от площади соприкосновения поверхностей, а зависит от силы давления N одной поверхности на другую, перпендикулярную плоскости соприкосновения тел:
.

Трение сцепления

Теперь рассмотрим статическую задачу. Пусть тело покоится, и на него действуют внешние силы с равнодействующей , приложенной под углом φ к нормали поверхности. Разложим ее на две составляющие: параллельную поверхности, и перпендикулярную . На тело также действуют сила реакции , перпендикулярная плоскости соприкосновения тел, и сила трения , которую при отсутствии скольжения называют силой сцепления. Сила сцепления направлена параллельно поверхности, препятствуя движению. Она может принимать значения от нуля до максимальной величины , определяемой аналогично (Т1):
(Т2) .
Здесь – статический коэффициент трения, который еще называют коэффициентом сцепления. Он не может быть меньше динамического коэффициента трения: .

Если , тело покоится. При этом сила трения сцепления меньше максимальной величины: . При , возникает движение. Когда , сила трения достигает предельной величины, возникает состояние предельного равновесия. Дальнейшее увеличение приводит к потере равновесия.

Сила трения сцепления – это сила трения скольжения, когда относительное перемещение соприкасающихся тел отсутствует.
Предельная сила трения – это максимальное значение силы трения сцепления.
Предельное равновесие – это состояние равновесия, при котором значение силы трения сцепления равно ее максимальному значению.

Из условий равновесия имеем: . Подставим в (Т2):
.
Отсюда получаем, что система будет находиться в равновесии, если
.
Видно, что условие равновесия зависит от угла φ , под которым приложена равнодействующая внешних сил, и не зависит от ее величины. Введем предельный угол трения: . Эту величину также называют просто углом трения. Тогда, условие равновесия можно записать так:
.
Это неравенство определяет конус в пространстве, который называется предельным конусом трения, конусом трения, или конусом сцепления. Если направление силы выходит за пределы этого конуса, то система начинает движение. Если направление силы попадает в конус сцепления, то система остается в состоянии покоя. Такое явление называется заклиниванием механизма.

Заклинивание механизма – это явление в механике, при котором система остается в состоянии покоя при любом, сколь угодно большом увеличении модуля внешней силы.

Условие возникновения движения при наличии трения
Для того чтобы тело начало движение, необходимо и достаточно, чтобы равнодействующая внешних сил находилась вне конуса трения.

Трение качения

Рассмотрим случай, когда одно из тел круглой формы катится без проскальзывания по поверхности другого. С точки зрения механики, такие тела соприкасаются в одной точке A . Площадь их соприкосновения бесконечно мала, в результате чего возникает бесконечно большое давление, которое не могут выдержать реальные материалы. Поэтому вблизи точки соприкосновения тел возникает деформация, которая имеет место только в небольшом участке соприкасающихся тел. В основной части тел, удаленных от точек соприкосновения, деформация практически отсутствует, и их можно рассматривать как абсолютно твердые тела. Тогда систему сил, возникающую в результате соприкосновения, можно привести к некоторой равнодействующей силе . При этом оказывается, что точка ее приложения смещена относительно оси симметрии катящегося тела. Это приводит к появлению момента сил относительно точки A , расположенной на оси симметрии круглого тела. Изучение деформированного состояния выходит за рамки теоретической механики. Поэтому мы приводим лишь результаты, применяемые в расчетах.

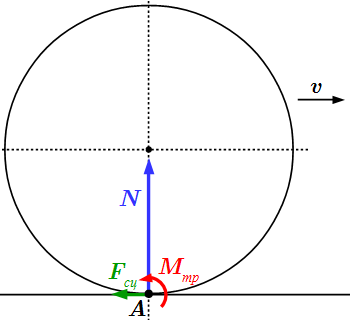
Расчетная схема трения качения.

1. Поскольку деформации, для небольших значений внешних сил малы, то, считают, что они не влияют на геометрические характеристики тел. То есть считают, что тела округлой формы соприкасаются в одной точке.
2. В точке соприкосновения, на тело действуют:
сила давления , перпендикулярная соприкасающимся поверхностям;
сила сцепления , лежащая в касательной плоскости, проходящей через точку соприкосновения поверхностей;
момент силы трения , препятствующий движению.
Максимальное значение момента силы трения определяется по формуле:
,
где δ – коэффициент трения качения, который имеет размерность длины.
3. Коэффициент трения качения зависит от соприкасающихся материалов и состояния их поверхностей. Он не зависит от кривизны поверхностей и угловой скорости вращения тела. А при движении с проскальзыванием, не зависит от скорости скольжения.

Центр тяжести тела

Центр тяжести в пространстве

Пусть тело состоит из n материальных точек. И пусть на каждую точку B_i действует сила тяжести , . Все силы тяжести, действующие на точки, параллельны. Поэтому мы имеем дело с параллельной системой сил. Как и для системы из двух однонаправленных сил, такая система сил имеет равнодействующую. Найдем ее.

Пусть – главный вектор. Поскольку все силы имеют одинаковое направление, то введем единичный вектор , направленный вдоль сил:
. Отсюда .

Найдем момент сил тяжести относительно произвольно расположенного центра O .
,
где
(ЦТ1) .

Отсюда видно, что формула вычисления момента имеет вид формулы момента от одной силы , приложенной в точке C . Точка C , положение которой определяется формулой (ЦТ1), называется центром тяжести тела. Таким образом, равнодействующая отдельных сил тяжести точек тела равна главному вектору силы тяжести, приложенному в центре тяжести. Модуль P равнодействующей называют весом тела.

Если бы мы находили равнодействующую сил тяжести, выполняя эквивалентные преобразования сил, то мы бы нашли только линию действия равнодействующей. Далее, если повернуть тело на некоторый угол, то можно найти другую линию действия равнодействующей. При этом все, подобным образом построенные линии, пересекаются в одной точке, которая и является центром тяжести тела.

Центр тяжести твердого тела – это точка, связанная с телом, через которую проходит линия действия равнодействующей сил тяжести частиц тела, при любом положении тела в пространстве.
Вес тела – это абсолютное значение равнодействующей сил тяжести частиц, составляющих тело.

Координаты центра тяжести определяются по формулам:
(ЦТ2) .
Здесь – абсолютное значение равнодействующей сил тяжести, или вес тела. – координаты точек тела. Эти формулы также можно записать в векторном виде.
.
Центр тяжести C связан с телом. Однако его положение может находиться за его пределами. Например, при наличии полости.

В случае, когда силы имеют другое происхождение, но также имеют одинаковое направление, то мы имеем дело с системой параллельных сил. В этом случае, точка C называется центром параллельных сил.

Для сплошного однородного тела, мы от суммирования переходим к интегрированию. Элементарная сила тяжести выражается через плотность ρ_i элементарной частицы тела, массой , и занимающей объем :
.
Здесь g – ускорение свободного падения. Переходя от суммированию к интегрированию, имеем:
(ЦТ3) .

Центр тяжести плоской фигуры

Рассмотрим плоскую фигуру. Выберем двумерную систему координат Oxy . Тогда положение центра тяжести определяется по тем же формулам (ЦТ2) и (ЦТ3), из которых нужно убрать переменную z .

Однородная фигура

Рассмотрим плоскую однородную фигуру. Для такой фигуры, плотность ρ является постоянной; сила тяжести Δp_i элементарной частицы пропорциональна площади ΔA_i этой частицы: Δp_i = ρΔA_ig . Вес P фигуры пропорционален площади A всей фигуры: P = ρAg .

Подставляя эти величины в формулы, определяющие положение центра тяжести находим:
.
Переходим от суммирования к интегрированию:
.
Мы видим, что сюда не входят плотность ρ и ускорение свободного падения g . Остались величины, зависящие только от геометрии сечения. Таким образом, для тела с постоянной плотностью, центр тяжести является геометрической характеристикой.

В этих формулах, y_C есть алгебраическое расстояние от центра тяжести до оси x ; y_k или y – алгебраическое расстояние элементарного участка до той же оси. x_C , x_k и x – соответствующие алгебраические расстояния до оси y . В этой связи вводят новую геометрическую характеристику сечения, которую называют статическим моментом.

Статический момент относительно некоторой оси – это сумма произведений элементарных площадей , входящих в состав фигуры, на алгебраические значения их расстояний до этой оси.

В рассматриваемом нами случае, статические моменты относительно осей x, y определяются по формулам:
.
Статические моменты широко используются при расчете конструкций. Для стандартных профилей, их значения указываются в соответствующих справочниках.

Центры тяжести простейших фигур

Параллелограмм, прямоугольник, квадрат: в точке пересечения диагоналей.
Треугольник: в точке пересечения медиан, которая делит каждую медиану в соотношении 1:2.
Дуга окружности с центральным углом 2α: .
Круговой сектор: .

Теоремы, применяемые при расчете центра тяжести

Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.

Если однородное тело имеет плоскость симметрии, то его центр тяжести находится в этой плоскости.

Центр тяжести фигуры, составленной из n более простых фигур, определяется по формуле:
(ЦТ4) .
Здесь – площадь всей фигуры; – площадь и координаты центра тяжести простой фигуры, входящей в состав сложной.

Способ отрицательных площадей (объемов)
Если k — я фигура вырезана из объемлющей ее части, то, в формуле (ЦТ4), соответствующая ей площадь считается отрицательной: .

Распределенная нагрузка

Силу тяжести протяженных тел, на схемах, изображают в виде эпюр. Также встречаются подобные силе тяжести параллельные силы, приложенные не в определенных точках тела, а непрерывно распределенные по его поверхности или объему. Такие силы называют распределенными силами или распределенными нагрузками.

Равномерно распределенная нагрузка q (рисунок А). Ее можно заменить равнодействующей силой величины , приложенной в центре тяжести эпюры. Поскольку, на рисунке А, эпюра представляет собой прямоугольник, то ее центр тяжести находится в центре основания эпюры – в точке C : | AC | = | CB | .

Линейно распределенная нагрузка q (рисунок В). Ее также можно заменить равнодействующей. Величина равнодействующей равна площади эпюры:
.
Точка приложения находится в центре тяжести эпюры. Центр тяжести треугольника, высотой h , находится на расстоянии от основания. Поэтому .

Приведение системы сил к центру

Теорема о параллельном переносе силы (лемма Пуансо)
Сила, действующая на данное тело, эквивалентна силе, полученной параллельным переносом исходной силы в любую точку тела и паре сил с моментом, равным моменту исходной силы относительно новой точки ее приложения.

Теорема о приведении системы сил к заданному центру
Любую систему сил, действующих на данное тело, можно привести к заданному центру O – то есть заменить одной силой, равной главному вектору, приложенной к точке приведения O , и парой сил с моментом M_O , равным главному моменту относительно центра O .

Статические инварианты

Такими инвариантами являются:
1) главный вектор ;
2) скалярное произведение главного вектора на главный момент .
Главный вектор равен векторной сумме всех сил и поэтому не зависит от центра приведения O . Главный момент зависит от положения центра O , относительно которого вычисляются моменты. Но величина его скалярного произведения на главный вектор не зависит от того, относительно какой точки вычисляется главный момент.

Хотя главный вектор не зависит от положения центра O , но величины его проекций на оси координат зависят от выбора системы координат. Поэтому они также не являются инвариантами. По той же причине и направление главного вектора не является инвариантом. Единственной численной величиной, которая не зависит от выбора системы координат, является модуль главного вектора. Но, в математическом отношении, проще иметь дело с квадратом модуля. Поэтому мы выберем его в качестве основного инварианта.

Итак, статическими инвариантами являются следующие величины:
– квадрат модуля главного вектора;
– скалярное произведение главного вектора на главный момент. Инвариантами также являются функции от инвариантов. Например, проекция главного момента на направление главного вектора является инвариантом:
.

Динама

Разложим главный момент на компоненту , параллельную главному вектору , и на компоненту , перпендикулярную :
(П1) .
Тогда .
Отсюда получаем упомянутый выше результат, что инвариантом является алгебраическая величина проекции главного момента на направление главного вектора:
.

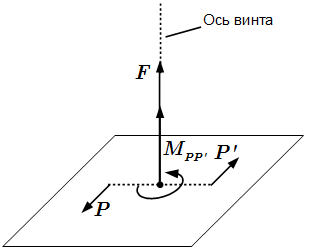
Динама – одна из простейших систем сил.

То есть, при изменении положения центра O , меняется вектор , в то время как вектор остается постоянным. Выбором центра приведения O , можно обратить в нуль. Тогда мы получим систему, состоящую из главного вектора и пары сил с моментом , лежащих в плоскости, перпендикулярной главному вектору. Такая система называется динамой или силовым винтом. Система приводится к динаме, если второй статический инвариант не равен нулю.

Динама – это простейшая система сил, состоящая из силы , приложенной к некоторой точке C , и паре сил, перпендикулярных . При этом момент пары параллелен линии действия силы. Динаму также называют силовым винтом, динамическим винтом, или статическим винтом.
Ось винта – это линия действия силы динамического винта.

Из (П1) мы находим, что минимальное значение модуля момента равно модулю его проекции на направление главного вектора:
.

Центральная ось системы сил

Пусть и – главный вектор и главный момент относительно некоторого центра O , который выберем за начало координат. И пусть второй инвариант отличен от нуля:
.
Найдем положение такой точки C , относительно которой система сил приводится к динаме. Для этого преобразуем главный момент от центра O к C :

.
Отсюда
(П2) .
Для динамы, векторы и направлены вдоль одной прямой. Поэтому
, где λ – некоторое число. Отсюда получаем два уравнения:
(П3) .
Пусть – компоненты вектора . Тогда подставив (П2) в (П3), имеем:
.
Это уравнение прямой в пространстве, которую называют центральной осью системы сил. Относительно точек этой прямой, система сил приводится к динаме, а главный момент имеет наименьшее по модулю значение.

Центральная ось системы сил – это прямая, обладающая тем свойством, что при приведении системы сил к любой из ее точек, система сил является динамой. При этом главный вектор и главный момент динамы параллельны этой прямой, а главный момент имеет наименьшее по модулю значение.

Приведение системы сил к простейшему виду

Пара сил

Пусть .
Тогда . Второй инвариант также равен нулю: . В этом случае, вектор главного момента не зависит от положения центра O . Система сил приводится к паре с моментом .

Если и , то это уравновешенная система сил. Она эквивалентна отсутствию сил.

Равнодействующая сила

Пусть .
В этом случае существует прямая, относительно точек которой главный момент равен нулю:
.
То есть система приводится к одной силе – равнодействующей, равной главному вектору приложенному к любой из точек упомянутой выше прямой. Эта прямая является линией действия главного вектора. Примеры: система сходящихся сил, система параллельных сил. Это системы, которые имеют равнодействующую.

Динама

При , как показано выше, система сил приводится к динаме.

Использованная литература:
А. А. Яблонский, В.М. Никифорова. Курс теоретической механики, часть 1, статика, кинематика. Москва, «Высшая школа», 1966.
С. М. Тарг, Краткий курс теоретической механики, «Высшая школа», 2010.

Автор: Олег Одинцов . Опубликовано: 03-10-2017 Изменено: 07-05-2020

Техническая механика

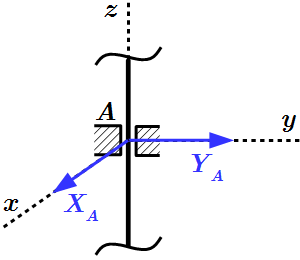
Пространственная система сил

Пространственная система сходящихся сил

Система сил, линии действия которых расположены в различных плоскостях, называется пространственной системой сил .

Пространственная система сил называется сходящейся , если линии действия всех сил системы пересекаются в одной точке.

Теорема: пространственная система сходящихся сил эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.

Пусть дана пространственная система n сходящихся сил (F₁, F₂, F₃. F_n) . На основании следствия из аксиом III и IV перенесем все силы системы вдоль линий действия в точку их пересечения. Затем на основании аксиомы параллелограмма последовательно сложим все силы и получим их равнодействующую:

Силовой многоугольник пространственной системы сил не лежит в одной плоскости, поэтому геометрический и графический способы нахождения равнодействующей пространственной системы сходящихся сил неприемлемы, а применяется только аналитический способ (метод проекций) .

Проекция силы на ось в пространстве находится по проецирующим перпендикулярам, и может быть определена при помощи тригонометрических функций. При определении проекций сил пространственной системы потребуется система координат с осями X , Y , Z , поскольку силы системы не располагаются в одной плоскости.

Правило знаков для проекций будет таким же, как и для плоской системы сил – совпадающие по направлению с координатной осью силы считаются положительными, в противном случае – отрицательными. Если вектор силы параллелен какой-либо оси координат, то он проецируется на эту ось в натуральную величину, если же вектор перпендикулярен оси, его проекция на эту ось будет равна нулю.

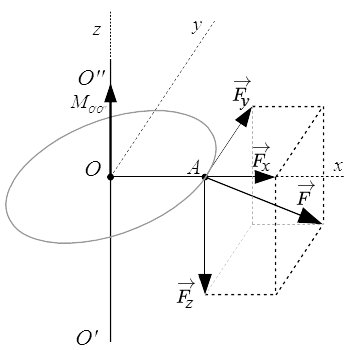
Разложение силы по трем осям координат

Пусть дана сила F (см. рисунок 1) .
Возьмем систему координат так, чтобы начало координат совпадало с началом вектора силы F (т. е. с точкой приложения силы). Из конца этого вектора опустим перпендикуляр на плоскость xy и разложим силу F на составляющие F_xy и F_z , а составляющую F_xy – на составляющие F_x и F_y . Тогда:

Достроим полученное изображение до параллелепипеда, у которого составляющие F_x , F_y и F_z являются ребрами, а сила F – диагональю.

Из изложенного можно сделать вывод: равнодействующая трех взаимно-перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах .

Из рисунка видно, что в случаях разложения силы F по трем взаимно-перпендикулярным направлениям x , y , z составляющие F_x , F_y и F_z равны по модулю проекциям силы F на эти оси.

Зная проекции силы на три взаимно-перпендикулярные оси координат, можно определить модуль и направление вектора силы по формулам:

модуль силы: F = √(F_x 2 + F_y 2 + F_z 2 ) (здесь и далее √ — знак корня) ;

направляющие косинусы: cos(F,x) = Fx/F; cos(F,y) = Fy/F; cos(F,z) = Fz/F .

Аналитический способ определения равнодействующей пространственной системы сходящихся сил

Рассмотренный выше способ разложения силы F на три составляющие по направлению координатных осей x , y , z можно применить для каждой из сходящихся сил пространственной системы. Тогда вместо данной системы n сходящихся сил мы получим эквивалентную ей систему 3n сил, из которых n сил действуют по оси x , n сил – по оси y , и n сил – по оси z .
Равнодействующая проекций сил системы на ось x равна их геометрической сумме, то же самое можно сказать и о равнодействующих проекций сил на оси y и z .
Таким образом, систему 3n сил можно заменить эквивалентной ей системой трех сил, каждая из которых представляет собой равнодействующую проекций сил данной системы на ту или иную ось координат.

Проекции силы на три взаимно-перпендикулярные оси и составляющие силы, направленные по этим осям, равны по модулю, следовательно, проекции равнодействующей равны:

Очевидно, что равнодействующая трех взаимно перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах, и по известным проекциям равнодействующей можно определить модуль и направление самой равнодействующей.

Аналитические условия равновесия пространственной системы сходящихся сил

Известно, что пространственная система сходящихся сил эквивалентна равнодействующей. Если такая система сил находится в равновесии, т. е. эквивалентна нулю, то можно сделать вывод, что равнодействующая этой системы равна нулю, а следовательно, и проекции равнодействующей тоже равны нулю, причем эти проекции равны сумме проекций составляющих.
Отсюда вытекают условия равновесия пространственной системы сходящихся сил:

ΣX = 0; ΣY = 0; ΣZ = 0 .

Эти условия формируются следующим образом: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую их трех координатных осей равнялась нулю.

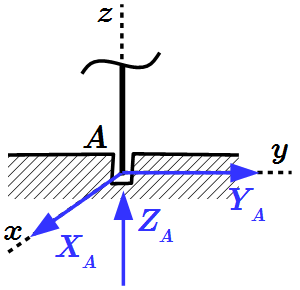
Момент силы относительно оси

Рассмотрим колесо червячной передачи, укрепленное на валу, вращающемся в подшипниках (см. рисунок 2) . Червяк передает червячному колесу силу F , не лежащую в плоскости, перпендикулярной оси.

Разложим силу F на три взаимно-перпендикулярные составляющие F₁ , F₂ и F₃ .
Составляющую F₁ назовем окружной силой , составляющую F₂ – осевой силой , а составляющую F₃ – радиальной силой .
Из рисунка видно, что составляющая F₁ вызывает вращательное действие, которое измеряется произведением силы F₁ на радиус колеса r ; составляющая F₂ стремится сдвинуть червячное колесо вдоль оси, а составляющая F₃ стремится изогнуть ось колеса.
Очевидно, что вращающее действие сил F₂ и F₃ относительно оси колеса равно нулю.
Таким образом, если нужно найти момент силы относительно оси, то следует принимать в расчет только составляющую F₁ , лежащую в плоскости, перпендикулярной оси, и не пересекающую ось (иначе ее момент будет равен нулю).

Ранее было отмечено, что проекция вектора силы на ось есть скалярная алгебраическая величина. В отличие от проекции на ось проекция силы на плоскость есть величина векторная, так как эта проекция характеризуется не только числовым значением, но и положением на плоскости, т. е. направлением.
Поэтому моменту силы относительно оси можно дать такое определение: моментом силы относительно оси называется величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.

Это определение поясняет рисунок 3 .
Момент силы относительно оси условимся записывать следующим образом:

Условимся считать момент силы положительным, если смотреть с положительного конца оси и сила стремится вызвать вращение против часовой стрелки, если же сила стремится вызвать вращение по часовой стрелке, ее момент считаем отрицательным.

Момент силы относительно оси не меняется при перемещении силы вдоль оси ее действия.

Момент силы будет равен нулю в двух случаях (не считая случаев, когда сила равна нулю или направлена вдоль оси):

• если вектор силы параллелен оси, так как при этом проекция силы на плоскость, перпендикулярную оси, равна нулю (см. рисунок 3, сила F_Z) ;
• если линия действия силы пересекает ось, так как при этом плечо равно нулю (сила F₃ на рисунке 2) .

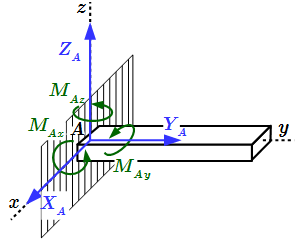
Аналитические условия равновесия пространственной системы произвольно расположенных сил

Пространственная система сил, в которой линии действия составляющих сил расположены произвольно, т. е. линии их действия могут не пересекаться и находиться в разных плоскостях, называется произвольно расположенной системой сил.

Для равновесия пространственной системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую из трех осей координат была равна нулю и чтобы алгебраическая сумма моментов всех сил относительно каждой из этих осей была равна нулю.

Строгое обоснование приведенного выше условия равновесия пространственной системы произвольно расположенных сил требует знания некоторых вопросов, не предусмотренных программами учреждений среднего профессионального образования, поэтому условие равновесия такой системы здесь приводится без доказательства.

Математически условие равновесия пространственной системы произвольно расположенных сил можно записать в виде уравнений:

• ΣX = 0; ΣMx(Fi) = 0;
• ΣY = 0; ΣMy(Fi) = 0;
• ΣZ = 0; ΣMz(Fi) = 0.

Свободное тело в пространстве имеет шесть степеней свободы, а именно: возможность перемещаться в направлениях трех взаимно-перпендикулярных осей координат и возможность вращаться вокруг этих осей. Таким образом, шести степеням свободы тела в пространстве соответствуют шесть условий равновесия.
Если система сил, приложенных к свободному телу, удовлетворяет всем шести условиям равновесия, то возможность трех перемещений и трех вращений тела под действием сил системы исключена, поэтому тело будет находится в равновесии.

Очевидно, что все выведенные ранее условия равновесия для различных систем сил являются частными случаями условия равновесия пространственной системы произвольно расположенных сил.

Так как условия равновесия пространственной системы сил справедливы для любых прямоугольных осей координат, то при решении данной задачи систему координат можно изменять, т. е. часть уравнений равновесия составить для одних осей координат, а часть – для измененных. В некоторых случаях этот прием упрощает решение задач.

Теорема о моменте равнодействующей относительно оси
(теорема Вариньона)

Теорема: момент равнодействующей относительно оси равен алгебраической сумме моментов, составляющих сил относительно этой же оси .

Пусть даны пространственная система n произвольно расположенных сил, приложенных к телу, и равнодействующая этой системы сил F_Σ (см. рисунок 4) :

Приложим к телу другую систему сил, равнодействующая которой F’_Σ по модулю равна F_Σ и направлена по той же линии действия, но в противоположную сторону, т. е. является уравновешивающей данной системы сил.
Тогда можно записать:

Так как обе записанные выше системы сил эквивалентны нулю, т. е. уравновешены, то к ним можно применить любое условие равновесия, например

Запишем это условие для обеих систем:

Так как правые части этих равенств равны, то будут равны и левые :

Сократив общее слагаемое M_x(F’_Σ) , получим: