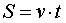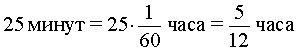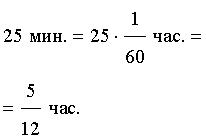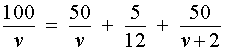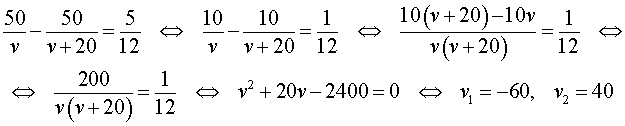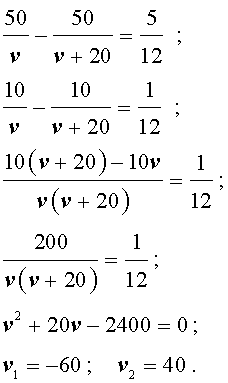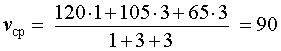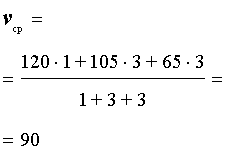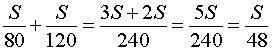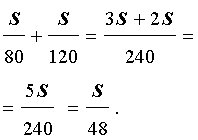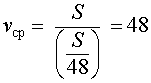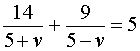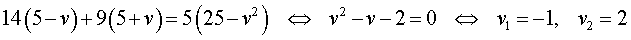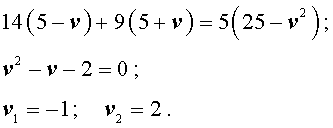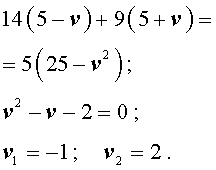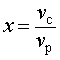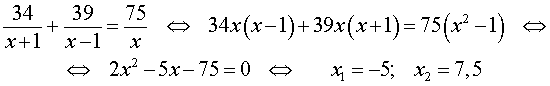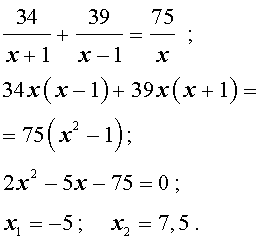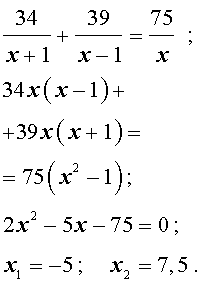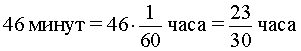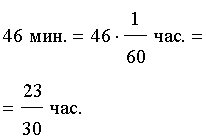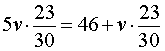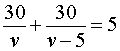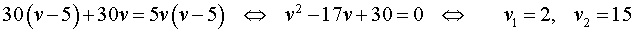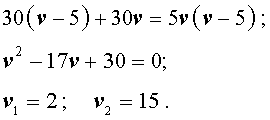Скорость течения реки составим уравнение

Задачи на движение

Скорость тела. Средняя скорость тела

Движение по реке. Скорость течения реки

Движение по кольцевым трассам

Скорость тела. Средняя скорость тела

Решение задач на движение опирается на хорошо известную из курса физики формулу

позволяющую найти путь S , пройденный за время t телом, движущимся с постоянной скоростью v .

Сразу же сделаем важное

Замечание 1 . Единицы измерения величин S , t и v должны быть согласованными. Например, если путь измеряется в километрах, а время – в часах, то скорость должна измеряться в км/час.

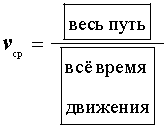
В случае, когда тело движется с разными скоростями на разных участках пути, вводят понятие средней скорости , которая вычисляется по формуле

Например, если тело в течение времени t₁ двигалось со скоростью v₁ , в течение времени t₂ двигалось со скоростью v₂ , в течение времени t₃ двигалось со скоростью v₃ , то средняя скорость

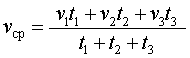(2)

Задача 1 . По расписанию междугородный автобус должен проходить путь в 100 километров с одной и той же скоростью и без остановок. Однако, пройдя половину пути, автобус был вынужден остановиться на 25 минут. Для того, чтобы вовремя прибыть в конечный пункт, водитель автобуса во второй половине маршрута увеличил скорость на 20 км/час. Какова скорость автобуса по расписанию?

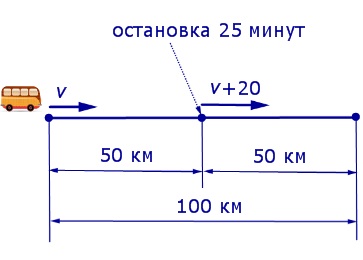
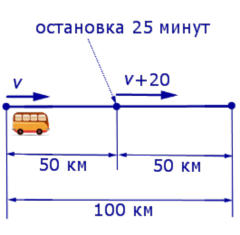
Решение . Обозначим буквой v скорость автобуса по расписанию и будем считать, что скорость v измеряется в км/час. Изобразим данные, приведенные в условии задачи 1, на рисунке 1.

– время движения автобуса по расписанию (в часах);

– время, за которое автобус проехал первую половину пути (в часах);

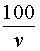
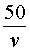
v + 20 – скорость автобуса во второй половине пути (в км/час);

– время, за которое автобус проехал вторую половину пути (в часах).

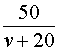
В условии задачи дано время остановки автобуса – 25 минут. Его необходимо выразить в часах, чтобы все единицы измерения были согласованными:

Теперь можно составить уравнение, исходя из того, что автобус прибыл в конечный пункт вовремя, а, значит, время, которое он был в пути, плюс время остановки должно равняться времени движения автобуса по расписанию:

Решим это уравнение:

По смыслу задачи первый корень должен быть отброшен.

Задача 2. (МИОО) Первый час автомобиль ехал со скоростью 120 км/час, следующие три часа – со скоростью 105 км/час, а затем три часа – со скоростью 65 км/час. Найдите среднюю скорость автомобиля на протяжении всего пути.

Решение . Воспользовавшись формулой (2), получаем

Ответ . 90 км/час.

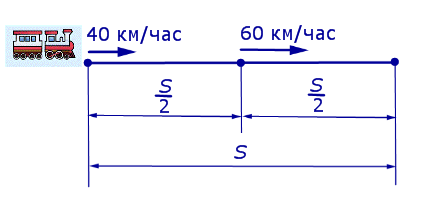
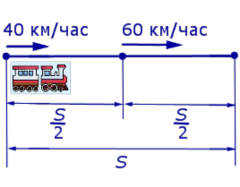
Задача 3 . Первую половину пути поезд шел со скоростью 40 км/час, а вторую половину пути – со скоростью 60 км/час. Найдите среднюю скорость поезда на протяжении всего пути.

Решение . Обозначим буквой S длину всего пути, выраженную в километрах. Изобразим данные, приведенные в условии задачи 3, на рисунке 2.

– время, за которое поезд прошел первую половину пути, выраженное в часах;

– время, за которое поезд прошел вторую половину пути, выраженное в часах.

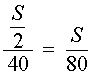
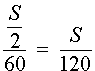
Следовательно, время, за которое поезд прошел весь путь, равно

В соответствии с формулой (1) средняя скорость поезда на протяжении всего пути

Ответ . 48 км/час.

Замечание 2 . Средняя скорость поезда в задаче 3 равна 48 км/час, а не 50 км/час, как иногда ошибочно полагают, вычисляя среднее арифметическое чисел (скоростей) 40 км/час и 60 км/час. Средняя скорость не равна среднему арифметическому скоростей, а является величиной, вычисляемой по формуле (1).

Движение по реке. Скорость течения реки

В отличие от задач на движение по суше, в задачах на движение по реке появляется новая величина – скорость течения реки.

По отношению к берегу, который неподвижен, скорость тела, движущегося по течению реки, равна сумме собственной скорости тела ( скорости тела по озеру, скорости тела в неподвижной воде, скорости тела в стоячей воде ) и скорости течения реки. По отношению к берегу скорость тела, движущегося против течения реки, равна разности собственной скорости тела и скорости течения реки.

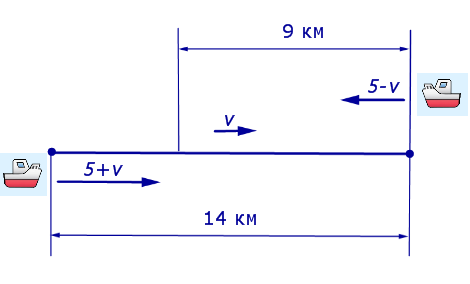
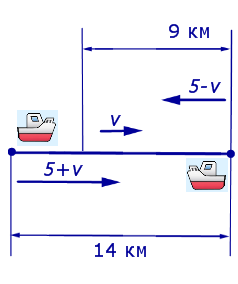
Задача 4 . Моторная лодка прошла по течению реки 14 км, а затем 9 км против течения, затратив на весь путь 5 часов. Скорость лодки в стоячей воде 5 км/час. Найдите скорость течения реки.

Решение . Обозначим буквой v скорость течения реки и будем считать, что скорость v измеряется в км/час.Изобразим данные, приведенные в условии задачи 4, на рисунке 3.

5 + v – скорость, с которой лодка шла по течению реки (в км/час);

– время движения лодки по течению реки (в часах);

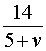
5 – v – скорость, с которой лодка шла против течения реки (в км/час);

– время движения лодки против течения реки (в часах);

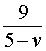
Теперь можно составить уравнение, принимая во внимание тот факт, что лодка находилась в пути 5 часов:

Решим это уравнение:

По смыслу задачи первый корень должен быть отброшен.

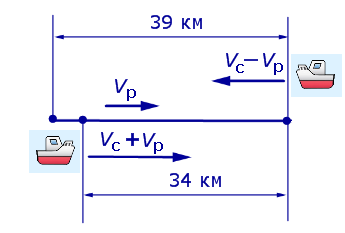
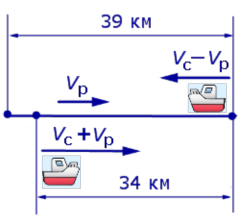
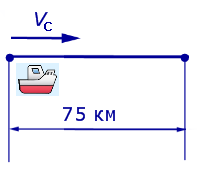
Задача 5. (Бюро «Квантум») Моторная лодка прошла по течению реки 34 км и 39 км против течения, затратив на это столько же времени, сколько ей нужно, чтобы пройти 75 километров в стоячей воде. Найдите отношение скорости лодки в стоячей воде к скорости течения реки.

Решение . Обозначим v_с (км/ч) скорость лодки в стоячей воде и обозначим v_р (км/ч) скорость течения реки. Изобразим данные задачи 5 на рисунках 4 и 5.

Учитывая тот факт, что в обеих ситуациях лодка провела в пути одно и то же время, можно составить уравнение:

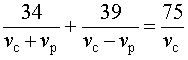(3)

Если ввести обозначение

то, воспользовавшись формулой

перепишем уравнение (3) в виде

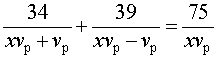(4)

Умножая уравнение (4) на v_р , получим

По смыслу задачи первый корень должен быть отброшен.

Движение по кольцевым трассам

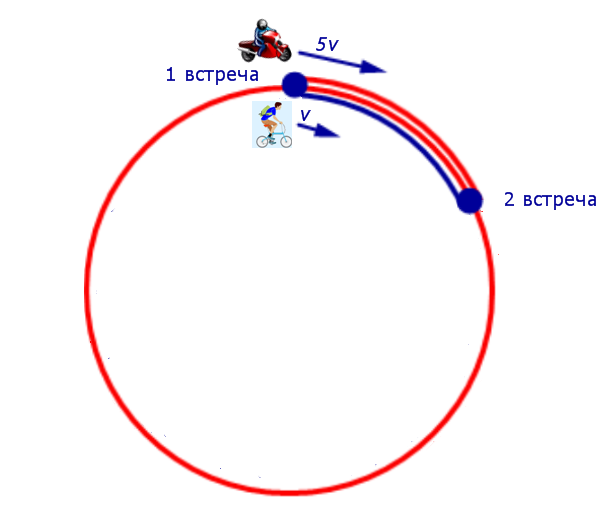
Задача 6. (www.reshuege.ru) Из пункта A круговой трассы длиной 46 км выехал велосипедист, а через 20 минут из пункта A следом за велосипедистом отправился мотоциклист. Через 5 минут после отправления мотоциклист догнал велосипедиста в первый раз, а еще через 46 минут после этого мотоциклист догнал велосипедиста во второй раз. Найдите скорости велосипедиста и мотоциклиста.

Решение . К тому моменту, когда мотоциклист в первый раз догнал велосипедиста, мотоциклист ехал 5 минут, а велосипедист ехал 25 минут, причем проехали они один и тот же путь. Отсюда вытекает, что скорость мотоциклиста в 5 раз больше скорости велосипедиста.

Таким образом, обозначив буквой v (км/час) скорость велосипедиста, получаем, что скорость мотоциклиста равна 5v (км/час).

В условии задачи дано время, прошедшее между двумя последовательными встречами мотоциклиста и велосипедиста, – 46 минут. Это время необходимо выразить в часах, чтобы все единицы измерения были согласованными:

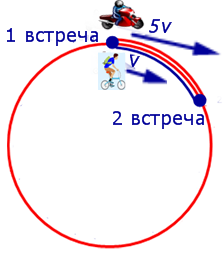
Изобразим данные задачи, касающиеся движения мотоциклиста и велосипедиста между первой и второй встречами, на рисунке 6.

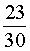
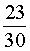
Поскольку за время часа, прошедшее от момента первой встречи до момента второй встречи, мотоциклист проехал 46 км (вся круговая трасса) плюс путь, который проехал велосипедист за часа, то можно составить следующее уравнение:

Решая это уравнение, находим скорость велосипедиста:

Ответ . Скорость велосипедиста 15 км/час, скорость мотоциклиста 75 км/час.

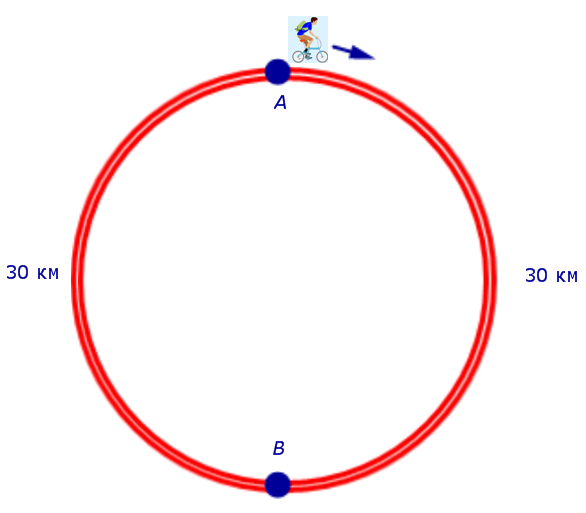
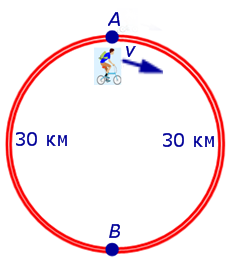
Задача 7 . На дороге, представляющей собой окружность длиной 60 км, пункты A и B являются диаметрально противоположными точками. Велосипедист выехал из пункта A и сделал два круга. Первый круг он прошел с постоянной скоростью, после чего уменьшил скорость на 5 км/час. Время между двумя прохождениями велосипедиста через пункт B равно 5 часам. Найти скорость, с которой велосипедист прошел первый круг.

Решение . Для определенности будем считать, что велосипедист двигался по кругу по часовой стрелке и рассмотрим рисунок 7.

Если обозначить буквой v (км/час) скорость, с которой велосипедист прошел первый круг, то скорость велосипедиста на втором круге будет равна v – 5 (км/час), и можно составить уравнение

Решая это уравнение, находим скорость велосипедиста на первом круге:

Поскольку скорость велосипедиста на первом круге больше, чем 5 км/час, то первый корень должен быть отброшен.

Ответ . 15 км/час.

Желающие ознакомиться с примерами решения различных задач по теме «Проценты» и применением процентов в экономике и финансовой математике могут посмотреть разделы нашего справочника «Проценты. Решение задач на проценты», «Простые и сложные проценты. Предоставление кредитов на основе процентной ставки», а также наши учебные пособия «Задачи на проценты» и «Финансовая математика».

Приемы, используемые для решения задач на выполнение работ представлены в разделе нашего справочника «Задачи на выполнение работ».

С примерами решения задач на смеси, сплавы и растворы можно ознакомиться в разделе нашего справочника «Задачи на смеси, сплавы и растворы».

С демонстрационными вариантами ЕГЭ и ОГЭ , опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.

Особенности решения задач на определение скорости течения реки. Примеры решений

Одними из увлекательных задач по математике и физике, которые предлагает учитель решить школьникам, являются задачи на определение скорости течения реки. В данной статье рассмотрим особенности решения этих задач и приведем несколько конкретных примеров.

О каких задачах пойдет речь?

Каждый знает, что вода в реке обладает некоторой скоростью течения. Равнинные реки (Дон, Волга) текут относительно медленно, небольшие же горные реки отличаются сильным течением и присутствием водяных воронок. Любой плавающий предмет, который брошен в реку, будет удаляться от наблюдателя со скоростью течения реки.

Люди, которые купались в реке, знают, что против ее течения плыть очень тяжело. Чтобы продвинуться на несколько метров, необходимо приложить намного больше усилий, чем при движении в стоячей воде озера. Наоборот, движение по течению осуществляется практически без каких-либо затрат энергии. Достаточно лишь поддерживать тело на плаву.

Все эти особенности позволяют сделать следующий важный вывод: если тело, имеющее в стоячей воде скорость v, будет двигаться в русле реки, то его скорость относительно берега будет равна:

• v + u для движения по течению;
• v — u для движения против течения.

Здесь u — скорость течения.

Если тело движется под некоторым углом к течению, то результирующий вектор его скорости будет равен сумме векторов v¯ и u¯.

Формулы, которые необходимо запомнить

Помимо приведенной выше информации, для решения задач на скорость течения реки следует запомнить несколько формул. Перечислим их.

Скорость течения является величиной постоянной, а вот скорость тела (лодки, катера, пловца) в общем случае может меняться, как по величине, так и по направлению. Для равномерного прямолинейного движения справедливой будет формула:

Где S — пройденный путь, v — скорость перемещения тела. Если движение происходит с ускорением a, тогда следует применять формулу:

Помимо этих формул, для успешного решения задач следует уметь пользоваться тригонометрическими функциями при разложении векторов скорости на составляющие.

Теперь перейдем к решению конкретных задач.

Задача с лодкой и рыбаком

Один рыбак решил отправиться на своей лодке без мотора вверх против течения реки на расстояние 2 километра. В стоячей воде он бы преодолел это расстояние за 30 минут, но при движении по реке ему понадобился целый час. Необходимо найти, чему равна скорость течения реки.

Поскольку скорость воды в реке является величиной неизвестной, то обозначим ее буквой x. Скорость лодки также неизвестна, однако ее можно вычислить, используя значения из условия для движения в стоячей воде. Получаем для скорости v лодки:

Мы нашли скорость, с которой рыбак на лодке может перемещаться по спокойному озеру. Чтобы найти скорость лодки против течения, необходимо из найденной величины вычесть значение x. Тогда для движения вверх по реке можно записать следующее равенство:

Выражаем отсюда значение неизвестного параметра, имеем:

Осталось подставить цифры из условия задачи и записать ответ:

Таким образом, скорость течения в реке в два раза меньше таковой для лодки.

Задача с моторной лодкой

Моторная лодка совершает каждый день переходы по реке из пункта A в пункт B. Дистанция между A и B составляет 7 км. Известно, что скорость лодки по течению равна 8 км/ч. Чему равна скорость течения, если на путь вниз по реке лодка затрачивает на 10 минут больше времени, чем при движении вверх по ней.

В данном случае мы не знаем ни скорость моторной лодки, ни скорость воды в реке. Обозначим первую как y, а вторую как x. Тогда можно записать следующие четыре уравнения:

Первое уравнение отражает скорость лодки по течению, второе и третье уравнения связывают время и скорость при движении вниз и вверх по реке соответственно. Четвертое уравнение следует из условия задачи о разности времен прямого и обратного пути между пунктами A и B.

Сначала найдем из этих уравнений время t₁ и t₂:

Для определения скорости x воды в реке вычтем из второго третье уравнение, получим:

Подставляем в это равенство рассчитанные величины t₁ и t₂, а также расстояние между пунктами S, получаем, что вода в реке течет со скоростью 0,64 км/ч.

Задача: движение катера под углом к течению

Теперь решим задачу, которая требует умения пользоваться тригонометрическими формулами.

Катер начал движение от одного берега реки к другому под углом 60 o к течению. Скорость катера в стоячей воде равна 10 км/ч. Скорость течения составляет 2 км/ч. Необходимо определить, на какое расстояние катер сместится вдоль берега, прибыв на противоположную сторону реки. Ширина русла реки равна 500 метров.

Данную задачу следует решать, разбив путь катера на две составляющие: перпендикулярную и параллельную берегу. Используя данные задачи, для перпендикулярной составляющей пути можно записать выражение:

Где v — скорость катера, S₁ — ширина реки. Подставляя данные, находим время, которое катер находился в пути:

Для вычисления параллельного берегу пути S₂ к горизонтальной проекции скорости катера следует добавить скорость течения, тогда соответствующее равенство будет иметь вид:

Подставляя известные величины, получаем ответ: катер вдоль берега пройдет путь 404 метра.

Как решать задачи на движение на ЕГЭ по математике 2019

Классическим примером текстовой задачи, которая может встретиться вам на ЕГЭ, является задача на движение. Эти задачи довольно разнообразны и включают в себя: задачи на движение навстречу, задачи на движение вдогонку, задачи на движение по реке. И поэтому вопрос, как же решать задачи на движение, иногда ставят учеников в тупик.

Научиться решать такие задачи довольно легко, для этого нужно знать алгоритм, состоящий всего из 3 шагов.

Формула, которую обязательно нужно знать, и секрет, как ее легко запомнить

Для решения любой задачи на движение вам обязательно нужно знать всего одну формулу, которая вам уже давно известна:И уметь правильно выражать из этой формулы скорость и время:Многие ученики путаются при записи этих формул, допуская ошибки. Чтобы раз и навсегда запомнить формулы нахождения расстояния, скорости и времени, просто нарисуй треугольник. В верхнем углу треугольника напиши S, а внизу — V и t. Проведи горизонтальную черту между ними. Теперь мы можем закрыть рукой ту величину, которую нам нужно найти, и увидим формулу нахождения этой величины. Например, нам нужно найти расстояние. Закрываем рукой S, и на нашем рисунке останется V t – это и есть формула нахождения расстояния. Или нам нужно найти время. Закрываем рукой t, и на нашем рисунке остается – формула нахождения времени. Нужно найти скорость? Закрываем рукой V, получаем – формулу нахождения скорости. Главное запомнить, что S должна быть в верхнем углу. Это можно сделать, например, с помощью ассоциации, что S похожа на змею, а змея – хозяйка горы, поэтому она на вершине. Вот как выглядит такой магический треугольник:

3 простых шага решения задачи на движение

Чтобы правильно решить задачу на движение нужно:

1. Определить неизвестное и составить таблицу на основании условия задачи.
2. Составить уравнение на основании таблицы.
3. Вернуться к условиям задачи и записать правильный ответ.

Давайте подробнее разберем каждый шаг:

1. Вначале нам нужно внимательно прочитать условие задачи и определить, что же взять за переменную Х. Чаще всего в задачах на движение удобнее всего за переменную Х обозначить скорость. Если же скорость нам прямо дана в условиях задачи, то за переменную Х обозначаем время. Если в условиях задачи прямо указаны значения и скорости, и времени, тогда за переменную Х берем расстояние. Затем из условий задачи определить все, что нам известно и занести в таблицу.
2. На основании полученной таблицы составляем уравнение и решаем его. После решения уравнения не торопимся записывать ответ. Ведь нахождение Х – это не всегда ответ к исходной задаче. Такую ошибку совершают многие ученики: фактически правильно решив задачу, они записывают неправильный ответ.
3. После решения уравнения возвращаемся к условиям задачи и смотрим, что же требовалось найти. Находим неизвестное и записываем ответ.

Задачи на движение бывают разными. В таких задачах участники движения могут двигаться навстречу друг другу, вдогонку, они могут двигаться по реке (против течения или по течению). Каждая из этих задач имеет особенности решения, о которых мы поговорим ниже и разберем на примерах.

Задачи на движение вдогонку: примеры с решением

При решении задачи, по условия которой оба участника движения двигаются в одном направлении, как правило, сравнивается время их движения. Необходимо запомнить правила:

1. Если время движения сравнивается (то есть присутствуют слова больше/меньше), то мы приравниваем время и прибавляем слагаемое. То есть чтобы получить большее время, мы прибавляем к меньшему времени что-то еще (из условий задачи).
2. Если условия задачи содержат общее время, то дроби, выражающее время, складываются.

Давайте разберем, как работают эти правила при решении задач.

Задача 1

Велосипедист и автомобилист одновременно выехали из пункта А в пункт Б, расстояние между которыми равно 50 км. Известно, что скорость автомобилиста на 40 км/ч больше, чем у велосипедиста, в результате чего автомобилист приехал в пункт Б на 4 часа раньше. Найдите скорость велосипедиста.

1. Необходимо определить, что взять за переменную Х и составить таблицу. Вспоминаем, что удобнее всего за Х обозначить скорость в том случае, если она прямо не указано в условиях задачи.

В нашем случае скорость в условиях задачи не указана, поэтому скорость велосипедиста обозначаем за Х.

Составляем таблицу, данные для которой берем из условий задачи.

Итак, расстояние (S) нам известно – 50 км, скорость велосипедиста – х, скорость автомобилиста на 40 км/ч больше, значит она равна х + 40. Чтобы определить время вспоминаем формулу t = S / V и подставляем в нее наши значения. Время, затраченное велосипедистом, получится 50 / х, а время, затраченное автомобилистом — 50 / (х + 40).2. На основании таблицы и условий задачи необходимо составить уравнение.

Из условий задачи нам известно, что автомобилист приехал раньше велосипедиста на 4 часа (смотрим наше первое правило). Это значит, что велосипедист затратил на 4 часа больше времени, чем автомобилист. Следовательно,

50 / (х + 40) + 4 = 50 / х

Решаем полученное уравнение, для этого приводим наши дроби к одному знаменателю:

50х + 4х (х + 40) – 50 (х+40) / х (х + 40) = 0

(50х + 4х 2 + 160х – 50х – 2000) / х (х+40) = 0

(4х 2 + 160х – 2000) / (х 2 + 40х) = 0

Умножим обе части уравнение на х 2 + 40х:

4х 2 + 160х – 2000 = 0

Разделим обе части уравнения на 4:

х 2 + 40х – 500 = 0

D = 40 2 – 4 * 1 * (-500) = 3600

Далее находим корни уравнения:

х₂ = — 50

3. Возвращаемся к условиям задачи и вспоминаем, что же требовалось найти.

Нам нужно было определить скорость велосипедиста, которую мы обозначили за Х.

Скорость велосипедиста должна быть положительна, поэтому х₂ не подходит по смыслу задачи. Следовательно, нас интересует только х₁ и скорость велосипедиста равна 10 км/ч.

Задача 2

Велосипедист выехал с постоянной скоростью из города А в город Б, расстояние между которыми равно 80 км. На следующий день он поехал обратно, при этом его скорость была на 2 км/ч больше прежней. По пути велосипедист останавливался и отдыхал 2 часа. В итоге на возвращение из города Б в город А у него ушло времени столько же, сколько на путь из города А в город Б. Найдите скорость велосипедиста на пути из города А в город Б.

1. Обозначим скорость велосипедиста на пути из города А в город Б как переменную Х.

Из условий задачи: расстояние — 80 км, скорость велосипедиста во второй день – х. Его скорость во второй день была на 2 км/ч больше, чем в первый день, т.е. в первый день она была ниже, следовательно, скорость велосипедиста в первый день равна х – 2. Определим затраченное велосипедистом время на путь по формуле t = S / V. Тогда время, затраченное в первый день на путь равно 80 / х, во второй день — 80 / (х + 2).2. На основании таблицы и условий задачи составим уравнение.

Из условий задачи нам известно, что во второй день велосипедист останавливался и отдыхал 2 часа, следовательно, в пути он провел на 2 часа меньше (смотрим наше первое правило). Также нам известно, что общее затраченное велосипедистом время в первый и во второй дни равно. Следовательно:

80 / (х + 2) + 2 = (80 / х)

Решаем полученное уравнение, для чего приводим дроби к общему знаменателю:

(80х + 160 – 80х – 2х (х+2)) / х (х + 2) = 0

Умножаем обе части уравнения на х (х + 2):

160 – 2х 2 + 4х = 0

— 2х 2 — 4х + 160 = 0

Делим обе части уравнения на -2:

D = 2 2 – 4 * 1 * (-80) = 4 + 320 = 324

Тогда корни уравнения равны:

3. Возвращаемся к условиям задачи. Нам необходимо было найти скорость велосипедиста на пути из города А в город Б, которую мы обозначали за Х.

Скорость должна быть положительна, поэтому х₂ = — 10 не подходит по смыслу задачи. Следовательно, скорость велосипедиста равна 8.

Задачи на движение навстречу: примеры с решением

Главное, что нужно помнить о движении навстречу: скорости участников движения складываются.

В тех случаях, когда нам неизвестно общее расстояние, то есть мы не можем его определить из условий задачи и из составленных уравнений, данное расстояние следует принимать за единицу.

Примеры решения задач на движение навстречу:

Задача 1

Из города А в город Б выехал автомобилист, через 3 часа навстречу ему выехал мотоциклист со скоростью 60 км/ч. Автомобилист и мотоциклист встретились на расстоянии 350 км от города А. Расстояние между городами А и Б равно 470 км. Найдите скорость автомобилиста.

1. Обозначим скорость автомобилиста как Х.

Автомобилист и мотоциклист встретились на расстоянии 350 км от города А. Следовательно, автомобилист проехал 350 км, а мотоциклист 470 – 350 = 120 км.

Составим таблицу:2. Составим уравнении на основании таблицы и условий задачи.

Из условий задачи известно, что автомобилист ехал на 3 часа дольше, чем мотоциклист (пользуемся первым правилом, которое разбирали при решении задач на движение вдогонку). Следовательно:

Решаем полученное уравнение:

3. Возвращаемся к условиям задачи. Нам необходимо было найти скорость автомобилиста, которую мы обозначали за Х. Следовательно, скорость автомобилиста равна 70 км/ч.

Задача 2

Из городов А и Б одновременно навстречу друг другу выехали автомобилист и велосипедист. Автомобилист приехал в город А на 6 часов раньше, чем велосипедист приехал в город Б. Встретились они через 4 часа после начала движения. Сколько времени затратил автомобилист на путь из города Б в город А?

1. Время автомобилиста обозначим как Х.

Примем расстояние между городами А и Б за единицу. Остальные данные берем из условий задачи.

Составим таблицу:2. Составим уравнение на основании таблицы и условий задачи.

Известно, что велосипедист и автомобилист встретились через 4 часа после начала движения и в сумме преодолели все расстояние от города А до города Б. То есть все расстояние от города А до города Б было преодолено за 4 часа.

Вспоминаем, что при движении навстречу скорости движения участников складываются. Подставим в формулу пути известные нам данные:

((1 / х) + (1 / (х — 6))) * 4 = 1

Решаем полученное уравнение:

(4 / х) + (4 / (х — 6)) = 1

Приводим дроби к одному знаменателю:

(4х — 24 + 4х — х 2 + 6х) / (х (х — 6)) = 0

Делим обе части уравнения на х (х — 6), при условии, что х > 6:

-х 2 + 14х — 24 = 0

Умножим обе части уравнение на -1:

х 2 — 14х + 24 = 0

Находим дискриминант нашего квадратного уравнения:

D = 14 2 – 4 * 1 * 24 = 100

Находим корни уравнения:

х₂ 2 + 40х – 40х – 200 = 0

3. Возвращаемся к условию задачи. Нам необходимо было найти собственную скорость катера, которую мы обозначили за Х. Так как скорость не может быть отрицательной, то х₁ = -15 противоречит условию задачи. Следовательно, собственная скорость катера равна 15 км/ч.

Задача 2

Моторная лодка вышла в 9:00 из пункта А в пункт Б, расстояние между которыми 30 км. Пробыв в пункте Б 3 часа, моторная лодка повернула назад и вернулась в пункт А в 20:00. Найдите скорость течения реки, если известно, что собственная скорость моторной лодки 8 км/ч.

1. Обозначим скорость течения реки за х. Остальные данные берем из условия задачи.

Составим таблицу:2. Составим уравнение.

Нам известно, что моторная лодка начала свое движение в 9:00, а закончила в 20:00, а также в течение этого времени пробыла без движения во время стоянки – 3 часа. Таким образом, общее время движения будет 20 – 9 – 3 = 8 часов. Когда речь идет об общем времени движения, то нам нужно сложить время движения по течению и время движения против течения (пользуемся вторым правилом, которое разбирали при решении задач на движение вдогонку). Получаем:

30 / (8+х) + 30 / (8-х) = 8

Решаем полученное уравнение. Для этого приводим дроби к общему знаменателю:

(30 (8+х) + 30 (8-х) – 8 (8-х) (8+х)) / (8-х) (8+х) = 0

Умножаем обе части уравнения на (8-х) (8+х):

240 + 30х + 240 – 30х – (64 – 8х) (8+х) = 0

480 – 512 – 64х + 64х – 8х 2 = 0

3. Возвращаемся к условию задачи. Нам необходимо было найти скорость течения, которую мы обозначили за х. Так как скорость не может быть отрицательной, то х₁ = -2 противоречит условию задачи. Следовательно, скорость течения равна 2 км/ч.

Итак, мы разобрались, как решать задачи на движения. В ЕГЭ 2019 помимо задач на движение могут содержаться и другие текстовые задачи: на смеси и сплавы, на работу, на проценты. О том, как их решать, вы можете узнать на нашем сайте.