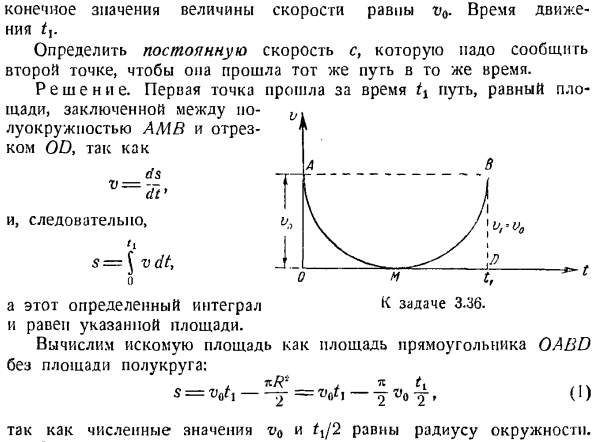
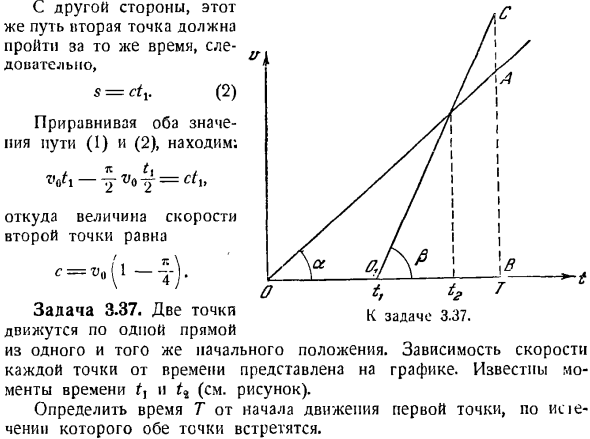
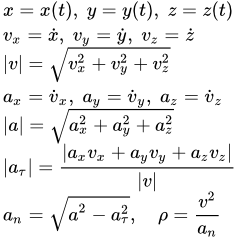Скорость точки равна от уравнения движения

Координатный способ задания движения точки

Введение

Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы применим основные результаты этой теории к координатному способу задания движения материальной точки.

Пусть мы имеем неподвижную прямоугольную систему координат с центром в неподвижной точке . При этом положение точки M однозначно определяются ее координатами (x, y, z). Координатный способ задания движения точки – это такой способ, при котором заданы зависимости координат от времени. То есть заданы три функции от времени (при трехмерном движении):

Далее мы приводим формулы вычисления кинематических величин и пример решения задачи для координатного способа задания движения.

Определение кинематических величин

Зная зависимости координат от времени , мы автоматически определяем радиус-вектор материальной точки M по формуле:
,
где – единичные векторы (орты) в направлении осей x, y, z .

Дифференцируя по времени , находим проекции скорости и ускорения на оси координат:
;
;
Модули скорости и ускорения:
;
.

Единичный вектор в направлении касательной к траектории:
.
Его можно определить двумя способами – по направлению скорости, или в противоположную сторону. Поэтому здесь в знаменателе стоит не модуль скорости, а алгебраическая величина скорости, которая, по абсолютной величине, равна модулю скорости, но может принимать как положительные, так и отрицательные значения: . Она является проекцией скорости на направление единичного вектора .

Алгебраическая величина тангенциального (касательного) ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории:
.
Вектор тангенциального (касательного) ускорения:
.
Здесь также, как и для скорости, – это скалярная величина, которая может принимать как положительные так и отрицательные значения: .

Нормальное ускорение:
.
Вектор нормального ускорения:
; .
Единичный вектор в направлении главной нормали траектории (то есть единичный вектор, перпендикулярный касательной и направленный к центру кривизны траектории):
.
Здесь – это модуль нормального ускорения: . Нормальное ускорение всегда направлено к центру кривизны траектории. Оно не может быть направлено в противоположную сторону.

Радиус кривизны траектории:
.
Центр кривизны траектории:
.

Единичный вектор в направлении бинормали:
.

Пример решения задачи

Определение скорости и ускорения точки по заданным уравнениям ее движения

По заданным уравнениям движения точки установить вид ее траектории и для момента времени найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.

Уравнения движения точки:
, см;
, см.

Решение

Определение вида траектории

Исключаем время из уравнений движения. Для этого перепишем их в виде:
; .
Применим формулу:
.
;
;
;
.

Итак, мы получили уравнение траектории:
.
Это уравнение параболы с вершиной в точке и осью симметрии .

Поскольку
, то
; или
.
Аналогичным образом получаем ограничение для координаты :
;
;

Таким образом, траекторией движения точки является дуга параболы
,
расположенная при
и .

Строим параболу по точкам.

0	6
± 3	5,625
± 6	4,5
± 9	2,625
± 12	0

Определяем положение точки в момент времени .
;
.

Определение скорости точки

Дифференцируя координаты и по времени , находим компоненты скорости.
.
Чтобы продифференцировать , удобно применить формулу тригонометрии:
. Тогда
;
.

Вычисляем значения компонент скорости в момент времени :
;
.
Модуль скорости:
.

Определение ускорения точки

Дифференцируя компоненты скорости и по времени , находим компоненты ускорения точки.
;
.

Вычисляем значения компонент ускорения в момент времени :
;
.
Модуль ускорения:
.

Алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории. Выберем направление совпадающим с направлением скорости . Тогда ; алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление скорости :
.
Поскольку , то вектор тангенциального ускорения направлен противоположно скорости .

Нормальное ускорение:
.
Вектор и направлен в сторону центра кривизны траектории.

Радиус кривизны траектории:
.

Траекторией движения точки является дуга параболы
; .
Скорость точки: .
Ускорение точки: ; ; .
Радиус кривизны траектории: .

Определение остальных величин

При решении задачи мы нашли:
вектор и модуль скорости:
; ;
вектор и модуль полного ускорения:
; ;
тангенциальное и нормальное ускорения:
; ;
радиус кривизны траектории: .

Определим остальные величины.

Единичный вектор в направлении касательной к траектории:
.
Вектор тангенциального ускорения:

.
Вектор нормального ускорения:

.
Единичный вектор в направлении главной нормали:
.
Координаты центра кривизны траектории:

Введем третью ось системы координат перпендикулярно осям и . В трехмерной системе
; .
Единичный вектор в направлении бинормали:

Автор: Олег Одинцов . Опубликовано: 22-02-2016 Изменено: 29-01-2020

Техническая механика

Скорость и ускорение

Скорость точки

В предыдущей статье движение тела или точки определено, как изменение положения в пространстве с течением времени. Для того чтобы более полно охарактеризовать качественные и количественные стороны движения введены понятия скорости и ускорения.

Скорость – это кинематическая мера движения точки, характеризующая быстроту изменения ее положения в пространстве.
Скорость является векторной величиной, т. е. она характеризуется не только модулем (скалярной составляющей), но и направлением в пространстве.

Как известно из физики, при равномерном движении скорость может быть определена длиной пути, пройденного за единицу времени: v = s/t = const (предполагается, что начало отсчета пути и времени совпадают).
При прямолинейном движении скорость постоянна и по модулю, и по направлению, а ее вектор совпадает с траекторией.

Единица скорости в системе СИ определяется соотношением длина/время, т. е. м/с .

Очевидно, что при криволинейном движении скорость точки будет меняться по направлению.
Для того, чтобы установить направление вектора скорости в каждый момент времени при криволинейном движении, разобьем траекторию на бесконечно малые участки пути, которые можно считать (вследствие их малости) прямолинейными. Тогда на каждом участке условная скорость v_п такого прямолинейного движения будет направлена по хорде, а хорда, в свою очередь, при бесконечном уменьшении длины дуги ( Δs стремится к нулю), будет совпадать с касательной к этой дуге.
Из этого следует, что при криволинейном движении вектор скорости в каждый момент времени совпадает с касательной к траектории (рис. 1а) . Прямолинейное движение можно представить, как частный случай криволинейного движения по дуге, радиус которой стремится к бесконечности (траектория совпадает с касательной) .

При неравномерном движении точки модуль ее скорости с течением времени меняется.
Представим себе точку, движение которой задано естественным способом уравнением s = f(t) .

Если за небольшой промежуток времени Δt точка прошла путь Δs , то ее средняя скорость равна:

Средняя скорость не дает представления об истинной скорости в каждый данный момент времени (истинную скорость иначе называют мгновенной). Очевидно, что чем меньше промежуток времени, за который определяется средняя скорость, тем ближе ее значение будет к мгновенной скорости.

Истинная (мгновенная) скорость есть предел, к которому стремится средняя скорость при Δt, стремящемся к нулю :

v = lim v_ср при t→0 или v = lim (Δs/Δt) = ds/dt .

Таким образом, числовое значение истинной скорости равно v = ds/dt .
Истинная (мгновенная) скорость при любом движении точки равна первой производной координаты (т. е. расстояния от начала отсчета перемещения) по времени.

При Δt стремящемся к нулю, Δs тоже стремится к нулю, и, как мы уже выяснили, вектор скорости будет направлен по касательной (т. е. совпадает с вектором истинной скорости v ). Из этого следует, что предел вектора условной скорости v_п , равный пределу отношения вектора перемещения точки к бесконечно малому промежутку времени, равен вектору истинной скорости точки.

Ускорение точки в прямолинейном движении

В общем случае движение точки с изменяющейся во времени скоростью называют ускоренным, при этом считая ускорение, вызывающее уменьшение скорости, отрицательным. Иногда движение, в котором скорость с течением времени уменьшается, называют замедленным.

Ускорение есть кинематическая мера изменения скорости точки во времени. Другими словами — ускорение — это скорость изменения скорости.
Как и скорость, ускорение является величиной векторной, т. е. характеризуется не только модулем, но и направлением в пространстве.

При прямолинейном движении вектор скорости всегда совпадает с траекторией и поэтому вектор изменения скорости тоже совпадает с траекторией.

Из курса физики известно, что ускорение представляет собой изменение скорости в единицу времени. Если за небольшой промежуток времени Δt скорость точки изменилась на Δv , то среднее ускорение за данный промежуток времени составило: а_ср = Δv/Δt .

Среднее ускорение не дает представление об истинной величине изменения скорости в каждый момент времени. При этом очевидно, что чем меньше рассматриваемый промежуток времени, во время которого произошло изменение скорости, тем ближе значение ускорения будет к истинному (мгновенному).
Отсюда определение: истинное (мгновенное) ускорение есть предел, к которому стремится среднее ускорение при Δt , стремящемся к нулю:

а = lim а_ср при t→0 или lim Δv/Δt = dv/dt .

Учитывая, что v = ds/dt , получим: а = dv/dt = d 2 s/dt 2 .

Истинное ускорение в прямолинейном движении равно первой производной скорости или второй производной координаты (расстояния от начала отсчета перемещения) по времени.

Единица ускорения — метр, деленный на секунду в квадрате ( м/с 2 ).

Ускорение точки в криволинейном движении

При движении точки по криволинейной траектории скорость меняет свое направление, т. е вектор скорости является переменной величиной.

Представим себе точку М , которая за время Δt , двигаясь по криволинейной траектории, переместилась в положение М₁ (рис. 1) .

Вектор приращения (изменения) скорости обозначим Δv , тогда: Δv = v₁ – v .

Для нахождения вектора Δv перенесем вектор v₁ в точку М и построим треугольник скоростей. Определим вектор среднего ускорения:

Вектор а_ср параллелен вектору Δv , так как от деления векторной величины на скалярную направление вектора не меняется.
Вектор истинного ускорения есть предел, к которому стремится отношение вектора приращения скорости к соответствующему промежутку времени, когда последний стремится к нулю:

а = lim Δv/Δt при t→0 .

Такой предел называют векторной производной.
Таким образом, истинное ускорение точки в криволинейном движении равно векторной производной скорости по времени .

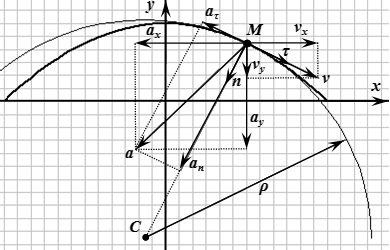
Из рисунка 1 видно, что вектор ускорения в криволинейном движении всегда направлен в сторону вогнутости траектории.

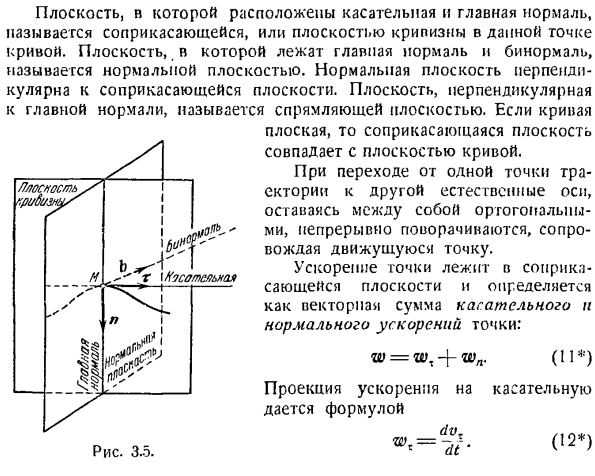
Так как векторную производную непосредственно вычислять мы не умеем, то ускорение в криволинейном движении будем определять косвенными методами. Так, например, если движение точки задано естественным способом, то применяется теорема о проекции ускорения на касательную и нормаль. Чтобы понять суть этой теоремы, следует рассмотреть понятие кривизны кривых линий.

Понятие о кривизне кривых линий

Рассмотрим криволинейную траекторию точки М (рис. 2а) .
Угол Δφ между касательными к кривой в двух соседних точках называется углом смежности .

Кривизной кривой в данной точке называется предел отношения угла смежности Δφ к соответствующей длине Δs дуги, когда последняя стремится к нулю.
Обозначим кривизну буквой k , тогда:

k = lim Δφ/Δs при Δs → 0 .

Рассмотрим окружность радиуса R (см. рисунок 2б) .
Так как Δs = RΔφ , то:

k = lim Δφ/Δs = lim Δφ/RΔs = 1/R (при Δs → 0) .

Следовательно, кривизна окружности во всех точках одинакова и равна k = 1/R .

Для каждой точки данной кривой можно подобрать такую окружность, кривизна которой равна кривизне кривой в данной точке. Радиус ρ такой окружности называется радиусом кривизны кривой в данной точке, а центр этой окружности – центром кривизны .

Итак, кривизна кривой в данной точке есть величина, обратная радиусу кривизны в данной точке :

Очевидно, что кривизна прямой линии будет равна нулю, а поскольку радиус кривизны такой линии равен бесконечности.

Теорема о проекции ускорения на касательную и нормаль

Проекция ускорения на касательную к траектории называется касательным (тангенциальным) ускорением, а проекция ускорения на нормаль к этой касательной – нормальным ускорением.

Теорема: нормальное ускорение равно квадрату скорости, деленному на радиус кривизны траектории в данной точке; касательное ускорение – первой производной от скорости по времени .

Доказательство этой теоремы основывается на геометрических построениях с учетом приведенных ранее зависимостей перемещения, скорости и ускорения от времени. В данной статье доказательство теоремы не приводится; при необходимости, его можно рассмотреть в других источниках информации.

Итак, на основании теоремы об ускорениях, можно записать:

ап = v 2 /ρ; a_τ = dv/dt .

Анализируя формулы касательного и нормального ускорения можно сделать вывод, что касательное ускорение характеризует изменение скорости только по модулю, а нормальное – только по направлению.

Зная величину нормального и касательного ускорения, можно вычислить полное ускорение точки, применив теорему Пифагора:

Направление ускорения: cos (a_τ,a) = а_τ/а .

Часто касательное и нормальное ускорения рассматривают не как проекции, а как составляющие полного ускорения, т. е. как векторные величины.

Вектор нормального ускорения всегда направлен к центру кривизны, поэтому нормальное ускорение иногда называют центростремительным .

Виды движения точки в зависимости от ускорения

Анализируя формулы касательного и нормального ускорений, можно выделить следующие виды движения точки:

а_п = v 2 /ρ ≠ 0; a_τ = dv/dt ≠ 0 , — неравномерное криволинейное (рис. 3а) ;

а_п = v 2 /ρ ≠ 0; a_τ = dv/dt = 0 , — равномерное криволинейное (рис. 3б) ;

а_п = v 2 /ρ = 0; a_τ = dv/dt ≠ 0 , — неравномерное прямолинейное (рис. 3в) ;

a_τ = dv/dt = const ≠ 0; а_п = v 2 /ρ ≠ 0 , — равнопеременное криволинейное (рис. 3г) ;

a_τ = dv/dt = const ≠ 0, а_п = v 2 /ρ = 0 , — равнопеременное прямолинейное (рис. 3д) ;

а_п = v 2 /ρ = 0; a_τ = dv/dt = 0 , — равномерное прямолинейное (движение без ускорения) (рис. 3е) .

Теоремы о проекциях скорости и ускорения на координатную ось

Если движение точки задано координатным способом, то путь (перемещение), скорость и ускорение за промежуток времени Δt можно найти, используя проекции этих величин на координатную ось. Очевидно, что приращение любой из координат при Δt стремящемся к нулю тоже стремится к нулю, и предел такого приращения может быть определен из дифференциальных отношений, устанавливаемых теоремами о проекциях скорости и ускорения:

Теорема: проекция скорости на координатную ось равна первой производной от соответствующей координаты по времени :

Теорема: проекция ускорения на координатную ось равна второй производной от соответствующей координаты по времени :

a_x = d 2 x/Δt 2 a_y = d 2 y/Δt 2 a_z = d 2 z/Δt 2 .

Зная проекции скорости или ускорения на координатные оси, можно определить модуль и направление вектора любой из этих величин, используя теорему Пифагора и тригонометрические соотношения.

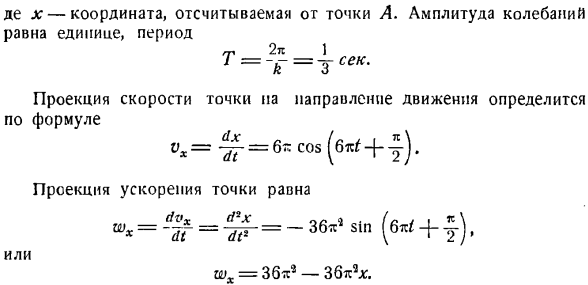
Скорость и ускорение точки

Точка скорость и ускорение Скорость точки-это производная по времени от положения r радиуса, которая определяет положение и пространство. Скорость точки характеризует изменение ее положения и времени ® = ТТ = с V ** + В + О. *） Вот, я, J, K-это ось. V, y, Z единичные векторы. Проекция скорости на ось фиксированных декартовых координат равна ДХ ды ДЗ. / G1AH 6) определите значения координат точек и любую константу интегрирования, используя момент nrsmspi. 7)

исключить время из уравнения движения и получить уравнение орбиты в координатной форме. Злое задание. , имел скорость v 8 км / С и цикл вращения T 1 час 36 минут, то есть 57 G0 секунд. Определите высоту полета спутника по поверхности Земли, предполагая, что орбита круговая и движение равномерное. Радиус Земли будет равен = 6370 км. Решение.

Первый спутник, запущенный в Советском Союзе в 1957/10/4 годах Людмила Фирмаль

Радиус орбиты спутника, проведенный от центра Земли, выражается буквой r, h x h — высота искомого спутника на поверхности Земли. Путь s, пройденный спутником за 1 Период вращения, равен произведению времени 7 «и расходуется на скорость v спутника, при 1 обороте, относительно выпуска 3.10.С другой стороны, тот же путь будет равен окружности радиуса R. Вт = 2-р、

Откуда? r = 7340 км. Мне. Далее найдите нужную высоту полета. ч = р-я = 7340-6370 = 970 км Задача 3.11. 2 точки перемещаются равномерно одна за другой По прямой линии с расстоянием между «скоростями» i, n и их начальным положением это было равносильно ок. Начались оба пункта. П3. Двигайтесь одновременно. А0 а. Определите время T. После этого 1 балл догонит задания 3.11, 3.12.

Еще одна вещь. Решение. Линия ОС и траектория движения. Уравнение движения для первой точки, которая выходит из O, является: Уравнение движения для 2-й точки, выходящей из Oit, выглядит следующим образом: С. 2 = в ^ Т -| — А0、 Отчет о координатах все еще должен выполняться из начальной точки O. столкновение происходит в момент времени T. ол = а.3Т или v

Пределы модулей скорости лодки с неограниченным увеличением во времени следующие: в — = Лим в = П. С. уз.- Задача 3. 16.Корабль движется в соответствии с уравнением, 0.055 / 50 тонн (1±.^ −0.055. / \ 1272.7 в — ’ М 50Т. Да.） The solution. To определите коэффициент скорости, вычислите абсолютное значение производной координат дуги относительно времени. _ _ O055 ^ 0i055 / 50 -■ 0.055 /•7 и> uij uyj- Да ДТ 1272.7 в.- 1 + 6е. 420___,, 0.055 / 1 + 6 * 0-0W / ■ Модуль начальной скорости судна определяется заменой t = 0 из(2). Версия v0 = 1У MjCCK. 50.(2）

Определите величину начальной скорости судна. Людмила Фирмаль

Задача 3. 16.Частицы, имеющие сухой заряд c, движутся в однородном электрическом поле переменной напряженности E = A $ \ r \ kt. Где A и K-постоянные коэффициенты. Форма уравнения движения частицы имеет вид Где t-постоянная. Определить величину скорости точки, ее начальное значение, а также максимальное и минимальное значения скорости. Решение.

Вычислите производную от x по времени, чтобы найти коэффициент скорости — (1-соѕ КТ). О, Боже мой. Тит-ТАТ. (1） Если мы подставим начальное значение времени£= 0 в уравнение (I)、 vQ = 0. Чтобы определить экстремальное значение коэффициента скорости, находим первую производную величины скорости относительно времени и считаем ее значение равным нулю, определяя время, за которое скорость достигает своего максимального и минимального значения. ДВ ДТ — Шин КТИ =0.м. В результате,//, = 0, r, 2n, 3ic,4zr, откуда Где ti = 0, I, 2, 3,… Подставляя значение найденного f в выражение(1), получаем следующее выражение: n-0 И если N = 1 (3） при последующих значениях n значения скорости(2)и(3)периодически повторяются.

Задача 3.17.Точка M движется по окружности радиуса r с постоянным тангенциальным ускорением, wv. At в первый раз точка была MQ, и скорость была равна нулю. Определите, в какой момент величина обычного ускорения будет представлять собой рампу тангенциального ускорения, и вычислите длину дуги, проходящей в этот момент. Решение. Равенство интеграции ДВ ДТ дифференциальный клапан. 1. \ > х = СГ (л） в w есть = const： vz = u> J + C, (2）

Где C — любая интегральная константа, определяемая из начального условия. Если /= 0, то подставляя эти значения в (2), т. к. C = 0、 В. = СШ. (3） Нормальное ускорение точки определяется по формуле _ ВЛ- ж * — р-р• Чтобы найти точку, в которой величины касательного ускорения и нормального ускорения равны, сделайте их значения равными Ж: Т \ Определите точку интереса Скорость точек(3) может быть представлена следующим образом:

При интеграции вы увидите следующее: с = м + с Постоянная C * определяется начальными условиями: для / = 0 a = 0. И затем… один. Предполагая, что I = tt в этом уравнении, мы находим искомое значение дуги. Вт. _гг — Т » — т- Задача 3.18.Нагрузка D подвешена на 2 кабелях£LS и / или BC, подвешенных на блоке BC. In исходное положение, отклоняющая стрелка ОС = с = 10 Дж / с л и АС = ВС. Расстояние между блоками Модуль скорости задается в Формуле в = в ^ + вл + вл. (3 *）

Направление скорости определяется направляющим Косинусом. потому что( j Wzk ’(5）

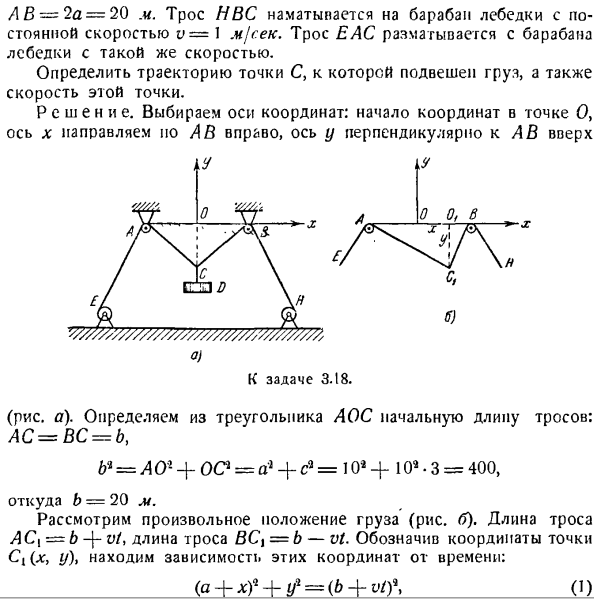
Проекция ускорения на неподвижную декартову ось с координатами раны ВХ = = Вайоминг-= г> вз = ^ з = ^(6 *） Коэффициент ускорения рассчитывается по формуле Вт—(- Вт и Вт «ручьи».(Г *） Направление ускорения определяется Косинусом направления. потому что («гдг)= -, потому что («0)==^, потому что(г * г)= ^. (8 *） Если уравнение движения задано в натуральном виде, то скорость точки равна LV = 2a = 20m. кабель NVS намотан на барабан лебедки с постоянной скоростью, v = I MjceK.

Кабель Эак намотан от барабанчика ворота на такой же скорости. Определите скорость движения этой точки, а также траекторию движения точки с, с которой будет подвешен груз. Решение. Выберите оси: начало координат точки O, направление оси x, где A B-это право, а y-ось перпендикулярна A B. Так… К заданию 3. 18. (Диаграмма а).Определите начальную длину кабеля от AOS треугольника. AC = BC = b、 Б * = АО * + ОС * = Д1-<- с * = 10 * + ж *. 3 = 400、 Где b = 20 м.

Введем значение найденной координаты l: в Формулу(1)для определения временной зависимости координаты Y. Е3 = 48-12-22 = о、 fs3 = 4 8-12-3 * =-60 м / с, i> s4 = 48-12•4 * = −144 MjceK. Эти значения определяют величину скорости в определенной точке time. To определив среднее значение скорости, нужно разделить пройденное расстояние на период, в течение которого этот отрезок расстояния passes. So скорость первой 1 второй точки будет: si — от 44 до 0. 、 , = = — J — = 44 м / с、

Где координаты точки времени t = \ sec, S | = = 48-1 −4•i3 = 44 м, начальные координаты s0 = .- 0.In таким же образом определяется значение средней скорости точки за следующую секунду. ая, — ое, 64-44 в * СР =〜ifzrt ^ = С-и— = 20 Micefc> с — с-36-64 нет, y3cP = 7 ^ 77 = — [- =м / с、 ficp = 7 -?7 = — 1 — =-100 MlceK- Знак минус указывает на то, что скорость направлена в отрицательную сторону. Затем найдите точку, в которой точка остановилась. Это означает, что формула для скорости (1) равна нулю. 48-12 / 2 = О、 Откуда? t * = болезнь 2 секунды

V-В=: К = Б — (10 *> если «r»,> 0, то точка движется в направлении, в котором значение a увеличивается. для r » m 0 точка движется в противоположном направлении в направлении, в котором значение A уменьшается. Ускорение в этом случае определяется проекцией на естественную координатную ось.

Естественная координатная ось, или естественное трехгранное тело траектории, представляет собой ортогональную (прямоугольную) систему координат, состоящую из оси/ 1. относительно а)/> она направлена на увеличение координат дуги, б)главная Нормаль направлена на вогнутость траектории, в) указанная/! Убедитесь, что 3 оси образуют правильную систему координат(рис. 3.5). В этот момент скорость точки равна нулю, а направление движения меняется на противоположное. =

При значении 2 секунды координаты точки равны s2 = 48•2-4•23 = 64 м. Время монотонно увеличивается, поэтому 2-й отрицательный маршрут должен быть отброшен, потому что он не имеет физического смысла. Определите среднее значение скорости за 4 секунды. Путь, по которому точка переместилась за 4 секунды, является суммой путей s * = 64.Путь переместился в первые 2 секунды, а точка переместилась в направлении отрицательной s в 3-й и 4-й секундах.

Этот метод заключается в следующем: при t = 4 s координаты точек были следующими: С4. 48•4-4•43 =-64 м. В результате на 3-й и 4-й секундах точка прошла путь / С4-С2 |-128 м. 4 секунды вообще, точка ушла далеко 64+ 128 = 192 м. Средняя скорость точек 192 lo, usr = — = 48 м / с Во-первых, следует отметить, что точка переместилась в сторону положительной оси s, и в этом направлении вдоль пути s5 = 64 м.

Затем точка переместилась на 128 м в противоположном направлении, а ее средняя скорость осталась постоянной по величине, и на этом участке пути была negative. As как видно из решения этой задачи, при определении средней скорости необходимо учитывать Если точка меняет направление движения точки, то необходимо учитывать тот факт, что движение состоит из всех движущихся участков пути, которые не могут быть равны разнице между координатами конца и начального положения точки.

Задача 3-23.Точка / VIt выбрасывается вертикально. Форма уравнения движения для точки при отсутствии сопротивления воздуха имеет вид х = х » (1） х. Где r> 0 и g-постоянные коэффициенты. Определяет скорость и ускорение точки, максимальную высоту точки и время, в которое точка достигает своего наивысшего положения. Решение.

Проекция скорости точки определяется как производная от временной координаты м> х = п-ГТ-(2） Проекция ускорения точки в прямолинейном движении равна производной проекции скорости времени или второй производной времени, отличной от координат Серии WX = = ЧХ = х = — г、 То есть ускорение точки является постоянной величиной. Из Формулы(2) видно, что ξ= 0 ’vx = vQ. Таким образом, константой является величина проекции скорости точки в первый момент.

Чтобы определить точку, в которой точка достигает максимальной высоты, используйте тот факт, что скорость точки в этом положении равна нулю. (2) указывает время нарастания через G. Поэтому время, когда точка достигает своего наивысшего положения, равно Т= -. (3） г в ’ Найти наибольшую высоту подъема h, подставив значение времени (3) в уравнение движения(1). для ВЛ

0 * 2 g * 2g ’ проблема 3.24.Mx точки, которые были брошены вертикально вверх с самого начала Скорость Zf0.

Через сколько секунд нужно подбросить Т вверх вертикально при начальной скорости 2-й точки с того же места Как обе точки встречаются в кратчайшие сроки от начала движения первой точки? уравнение движения то’ки подбрасывается вертикально вверх、 Отсутствие сопротивления воздуха икс= — Где v0-начальная скорость точки, А g-ускорение свободного падения. The solution. At на первый взгляд может показаться, что 2-я точка бросается одновременно с первой точкой.

Однако скорость 2-й точки очень мала, и к тому времени, когда первая догоняет ее, она падает на высоту Земли. Поэтому выбор момента во времени для приведения 2-й точки играет важную роль. 2-я точка Mit будет бросать вверх после того, как начальная скорость первой точки будет низкой t секунд, поэтому можно будет просто переместить первую точку обратно вниз. Давайте попробуем

Если точка меняет направление движения точки, то необходимо учитывать тот факт, что движение состоит из всех движущихся участков пути, которые не могут быть равны разнице между координатами конца и начального положения точки. Задача 3-23.Точка / VIt выбрасывается вертикально.

Форма уравнения движения для точки при отсутствии сопротивления воздуха имеет вид х = х » (1） х. Где r> 0 и g-постоянные коэффициенты. Определяет скорость и ускорение точки, максимальную высоту точки и время, в которое точка достигает своего наивысшего положения. Решение. Проекция скорости точки определяется как производная от временной координаты м> х = п-ГТ-(2）

Проекция ускорения точки в прямолинейном движении равна производной проекции скорости времени или второй производной времени, отличной от координат Серии WX = = ЧХ = х = — г、 То есть ускорение точки является постоянной величиной. Из Формулы(2) видно, что ξ= 0 ’vx = vQ. Таким образом, константой является величина проекции скорости точки в первый момент.

0 * 2 g * 2g ’ проблема 3.24.Mx точки, которые были брошены вертикально вверх с самого начала Скорость Zf0.

At на первый взгляд может показаться, что 2-я точка бросается одновременно с первой точкой. Однако скорость 2-й точки очень мала, и к тому времени, когда первая догоняет ее, она падает на высоту Земли. Поэтому выбор момента во времени для приведения 2-й точки играет важную роль. 2-я точка Mit будет бросать вверх после того, как начальная скорость первой точки будет низкой t секунд, поэтому можно будет просто переместить первую точку обратно вниз. Давайте попробуем

Время, в течение которого первая точка перемещается с самой высокой позиции на встречу со 2-й точкой. Тогда путь, который спускался к первой точке во время tlt, был бы: s — ^ 1 — 2〜* Время от момента, когда первая точка находится в своем наивысшем положении до момента, когда 2-я точка начинает двигаться, представлено Z. затем путь до 2-й точки достигает первой точки Два С. 1 = ВЛ(м-х）

В момент tx точка была заполнена, поэтому、 Си + Си = ч,(1） Где h-наибольшая высота первой точки и равна v% j2g (см. предыдущую задачу).Затем, подставив значение (1) всех величин, можно увидеть следующее: Если мы рассматриваем это уравнение как неявную зависимость tl — /(x), мы находим производную tx относительно m, приравнивая эту пулю. ДХ фдж ГЗ Откуда? Ho Vi / g равно времени подъема 2-й точки На наибольшую высоту (см. выпуск 3.23).

Поэтому на момент встречи 2-й пункт будет самым высоким. Назначьте найденное значение tx- (3) Формуле(2).Затем, когда вы бросаете такой член, вы видите следующее: л. 2г-2-т-2г> Где назначенное время 1.• Тл == Тогда из Формулы(3)можно увидеть: — Ви + yvT-в * £ С момента броска первой точки необходимо поднять 2-ю точку, после чего, чтобы найти требуемое время моль, необходимо добавить время t0t, при котором первая точка достигнет наивысшего положения. Дж г 1 г Из Формулы(4)、 для R М> 0″5> 2р;>, для M = 0 ИС и ВН = 2В-в、

Поэтому, если вы бросаете 2-е очко、 Как первая точка достигла наивысшего положения? Когда 2-я точка брошена, прежде чем первая точка находится в своем самом высоком положении. Также, если m = 0, то 2-я точка выбрасывается в тот момент, когда первая эструс находится на самом высоком уровне. Задача 3.26.Линии ellipsography АВ = 1 слайды заканчиваются на горизонтальной оси, а конец Б по вертикальной оси. Вам будет дана линейка Да.

Задание 3.25 к. Кривошип закреплен шарниром посередине, в движении по ОС = 0,5/.Расстояние AM = ay VM = b известно. Угол (2d. Уравнение движения точки в, проекция скорости и ускорения на координатные оси, касательная линия, нормальное ускорение, суммарное ускорение, а также определяют радиус кривизны траектории любого положения механизма. определите координаты точки B при cp = 0 и cp = r, скорость, ускорение и радиус кривизны ее траектории. Решение. Поскольку OA = ON = r, треугольник OAN равнобедренный. Поэтому Оан = О. Я! = 90° —

Равенства определяют проекцию скорости оси абсцисс в зависимости от координат точек. чтобы определить проекцию скорости на ось y, подставим значение (G), найденное в Формуле (2).И затем… ва. икс м- — — ш -, (7） 7 лет » Или, если вы введете значение y в (1)в это уравнение, вы можете увидеть, что: П = ±ВТН. (8） Чтобы рассчитать проекцию ускорения на ось абсцисс, дифференцируем зависимость (6) со временем, помня, что v = const. ва. ва ва. x v-a9, x / Лига Чемпионов х = — г — — — й * — Ш— — — — — Г-ш -. (9） У3 * у у У3 а в 7

Чтобы определить проекцию ускорения на продольную ось, вычислите производную 2-го порядка по времени в продольной координате с помощью (8). Р = — ВФ (10） СН2-с Учитывая (G), узнайте ниже. в ВА В * А9 / 11н гл’^ Но… Чтобы найти ускорение точки, используйте следующую формулу ж * = 1п-+ — У3, (12） Тангенциальное ускорение характеризует изменение величины скорости. Если величина скорости не изменится, то она будет равна zero.

In кроме того, он исчезает, когда скорость достигает экстремального значения. Нормальное значение ускорения определяется по формуле Где P-радиус кривизны траектории. Нормальное ускорение характеризует изменение скорости direction. In в обоих случаях радиус кривизны бесконечен, поэтому он равен точке перегиба пули и траектории линейного движения пули. point. In кроме того, обычное ускорение исчезает в точке m> = 0.

Коэффициент ускорения рассчитывается по формуле Вт = В ^ + ^ К = +(Джей-Джей.(14 *） Направление ускорения определяется Косинусом направления. потому что(ш? х)^, потому что(МАС Н)=(15 *） После простого преобразования подставим (9) и (11). 2 ТВ-А2 \ <. о Х \ Фольксваген, о Х / 10ч Яг = — ч 1 4-СЛР ->= — м-ч -. (13） \ J В\и> V Если вы снова используете равенство (I) и извлекаете квадратный корень из (13), вы найдете значение ускорения точки. (14） г-в. Из-за этого условия точка движется с постоянной скоростью, поэтому максимальное ускорение одновременно является и нормальным ускорением. О3 / 1GCH з = ЗП = Дж. (15）

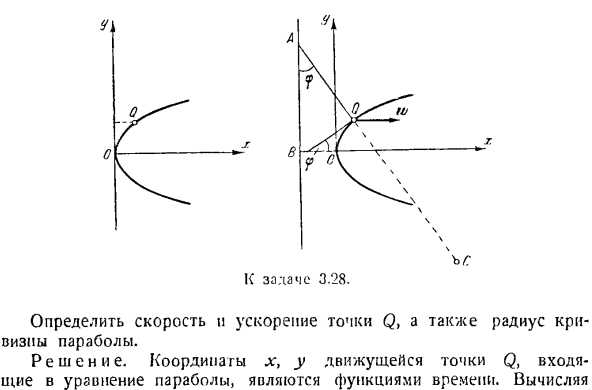
Определите радиус кривизны цепной линии, сравнив равенства (14) и (15) р = 4-(с） Эта задача может быть решена путем прямого дифференцирования уравнения цепной линии без передачи его в гиперболическую функцию. Однако это решение будет более длительным. Задача 3.28.Поскольку точка Q движется вдоль параболы y2-2px, положение проекции на продольную ось задается уравнением y = ct. K * выпуск 3.28.

Определите скорость и ускорение точки Q, а также радиус кривизны параболы. Решение. Координаты X и y движущейся точки Q в уравнении параболы являются функцией time. By вычислительная техника с. 0. \ Производные по времени с обеих сторон параболического уравнения、 2У = 2 пикселя Или yvyбыл = данные. (1） С другой стороны, если мы дифференцируем по времени y = ct>, мы можем видеть, что: Р = уу = С. Тогда из (1)： Зет. х р ’ Поэтому скорость точек определяется соотношением v = = 1(2）

Предсказание ускорения осей координат может быть получено с помощью следующего уравнения. С2 и> х = = — г = Дж = const и、 Вайоминг = ты = 0. Таким образом, коэффициент ускорения абсолютной точки равен С2 Вт = WX с Я я =-. Если обозначить угол между касательной параболы и осью x буквой В * _ _ _ _ в * п Откуда? Рассматривая P wn W j siri ’f F C2 I Sin cp j’ или(2), получаем следующее: Р =(3） Р / Син? Мне. в’ Восстановление в точке D на расстоянии OB = p / 2 От точки о перпендикулярно оси абсцисс(направление параболы)

Найти точку A, где этот перпендикуляр пересекает pores. It меньше, чем траектория точки. И затем… / ОБЕСПЕЧЕНИЕ КАЧЕСТВА.- =|- G. (4） 1 ^ 1 | грех ’ Ф | Если сравнить равенство (3) и равенство (4), то можно увидеть, что: ？ = \ \ КК = 2 \ ОК \、 Где точка С является центром кривизны. Задача 3.29.Точка Л1 движется по уравнению вы = Г = Е ((потому что Т греха т \ с V2 = я•= — В * = Е ’] / Т р х » г » г Определите проекцию ускорения точки. серии WX = х = — 2С <греха Т гор = г = 2эц потому что Т, вз-з-Эл.

Абсолютное значение ускорения равно Тангенциальное ускорение определяется как производная скорости по времени. Найти его нормальное ускорение, учитывая максимальное ускорение точки и величину касательного ускорения В2 = ш \ — [- з-н -、 Откуда? Вт н = ж * — ж \ = УО *-?> ЕV = 2е＃ Следовательно、 ЗП = Эль г л \ Введите значение скорости и нормального ускорения в Формулу(1), и вы увидите радиус кривизны траектории （）= ’-= −7-= ТГ-В-2 *. (3） Радиус кривизны и нормальное ускорение являются важными характеристиками движения точки.

В этой задаче из Формулы (3) видно, что за счет неограниченного увеличения времени радиус кривизны увеличивается бесконечно. Однако, как видно из (2), нормальное ускорение не стремится к нулю при неограниченном увеличении времени, а, наоборот, увеличивается без неограниченного количества времени.

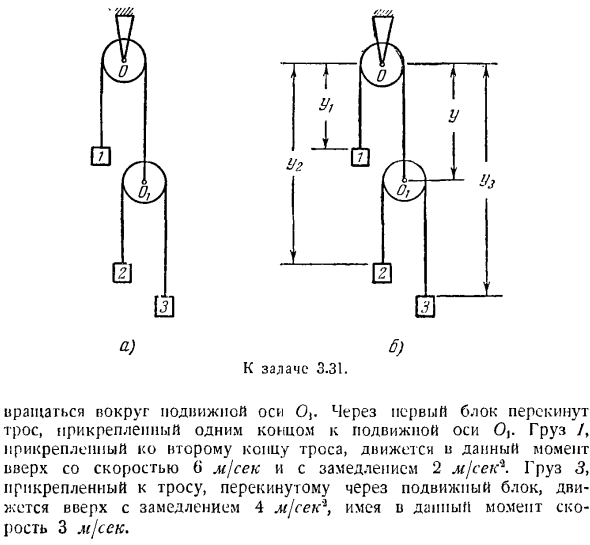
Траектория точки, определяемая параметрическими уравнениями движения, представляет собой логарифмическую спираль, радиус ее кривизны бесконечно увеличивается со временем. Задача 3.31.Система состоит из 2 блоков(рисунок а), 1 может вращаться вокруг неподвижной оси О, а 2-й Один. м. т. Так… Я… Так… □ Да. □ Узу В 0. в б.） один.） Крейс 3.31. Вращающийся вокруг подвижной оси o трос, прикрепленный к одному концу подвижной оси O, перекидывается через первый блок.

Груз, прикрепленный ко 2-му концу троса, теперь движется вверх со скоростью 6 м / с с замедлением 2 м / с.Груз 3, установленный на тросе, подвешенном на подвижном блоке, движется вверх с уменьшением на 4 м / с, и в данный момент он составляет 3 м / с. Важным частным случаем движения является движение равномерное и колеблющееся equally. In равномерное движение, скорость постоянна. Уравнение движения с постоянной скоростью о = о о + ви,(16 *） Где o — координата дуги точки, отсчитанной от начала координат, а o0-значение координаты дуги в точке/=.

При равном знакопеременном движении тангенциальное ускорение точки является постоянным по величине. Уравнение равного движения выглядит так: ^^ ОРВ + ^ Ф. Клеммник (J7 *） Зависимость времени от движения, при котором скорость изменяется равномерно, определяется уравнением на VX = v0 в + СШ. (18 *） Если перемещение определяется уравнениями (17 *) и (18)、

Если это движение равно, то оно будет равномерно ускорено Медленно двигаться (^^> 0). в общем случае при ускоренном движении тангенциальное ускорение совпадает по знаку с проекцией скорости по касательной direction. In при замедленном движении существует знак, противоположный касательному направлению ускорения и проекции скорости на касательную. Соотношение между скоростью и расстоянием, пройденным равными чередующимися движениями, определяется формулой Галилея И что? = вл + 2wx(о-ц0). Часто задача заключается в нахождении радиуса кривизны траектории. Р

адиус кривизны траектории можно определить по формуле (13). В V2. Р = 1 -. (19 ） Найти скорость и ускорение центра движущегося блока, точку Oi, удельную временную нагрузку 2. Решение. Порядковый координата груза показана на буквы Г, ый, ый, и точку o (рис. 6). ’Длина кабеля между нагрузкой Y и центром блока Oj остается неизменной、 Г \ «лы-Т-константный、 Где буква R обозначает радиус блока. Аналогично, длина кабеля, соединяющего нагрузку 2 и 3, одинакова. Представляет длину этого кабел

я Если вы различаете оба уравнения Uch-Y » Uz-y — \ — zr = const по времени, вы можете видеть, что: )> 1-hL-2 > > = 0. Если подставить указанные значения I-speed px и ul, то получится: если мы получим дифференциальное уравнение (1) относительно времени p =-6 m j секунд,= — pa =-15 m /s, то: Йи + Дж? а-2Д)= 0 Вводя известные значения ускорения yx в эти уравнения, мы видим, чт

о: y = 2 м / с, = 2y-Z’Z = 8 м / с . Таким образом, скорость#и ускорение в точке Ox равны скорости и ускорению груза/, направленного в противоположную сторону. Скорость движения груза 2 Пи равна 15 м / с в направлении вниз, а ускорение этого груза равно 8 м / с в направлении вверх Задача 3.32.Ускорение точки составляет 12 ТМ-сек. оно направлено в отрицательном направлении вдоль оси v. t =(через 2 секунды скорость точки была рав

на b М / с, направленной в положительном направлении вдоль x-axis. AT t= 3 секунды, точка находилась на оси Х на расстоянии 50 м от исходного положения. Определите уравнение движения точки. Решение. Поскольку точка движется линейно вдоль оси x, ускорение проекции на ось x равно

Это уравнение выражается в следующем виде поразил =-12 / » ДТ (я） Умножив обе части на dt, заметим, что _ dj Д ^ х DT *

ДТ ’ Формула (1) для интегрирования. л ’= — «’ + с,. (2） Чтобы определить любую интегральную константу C, используйте условие

еременных в Формулу(2), то можно увидеть следующее: Г =-6•23 + М Или С,= 30. Уравнение (2)принимает вид §ВБ/ * 4з. Если мы умножим обе стороны этого уравнения на dt, это выглядит так: ДХ =-60 ДТ 30 ДТ. При интеграции вы получаете следующее: л- = −2 / ’ — (- 30г + с *.(3） Любая интегральная константа C! Для определения T введем в Формулу (3) условие n = 50m для каждой F = 3 секунды. 50 =-2•27 + 30•3 +Съ Отсюда С,=И. Введите это значение в уравнение(3)и вы найдете уравнение движения для точки * = −2/3 + 30 / — f 14. Задача 3. 33. В течение 20 секунд скорость судна, движущегося (циркулирующего) по дуге радиусом 200 м, падает с 15 до 12 м / с. Предположим, что величина тангенциального ускорения пропорциональна степени 2 скорости,

и определим nyib и круговой угол, пройденный за первые 10 секунд. Решение. Так как тангенциальное ускорение корабля пропорционально мощности 2 скорости、 — =\КВ(1） Где h-коэффициент пропорциональности, величина которого неизвестна. Когда вы изолируете переменную, вы видите следующее: дифференциальный клапан. виджей. Чтобы найти коэффициент k, воспользуемся условием, что в течение 20 секунд скорость судна падает с 15 до 12 м / с. Если проинтегрировать уравнение (1) в этих пределах, то оно выглядит так: 11, 10. И

ли 15. 12. _ _ _ В. = 2 0 / г、 Откуда? 12 \ 5〜 1/1200. Кроме того, определите траекторию, по которой двигался корабль в первые 10 секунд. Для этого сначала (1) Находим по Интегралу от скорости как функции времени. У нас есть： —- С = КТ. (2） В. Чтобы определить любую интегральную постоянную, нужно использовать начальные условия движения: для = = 0, скорость v = vQ. Если ввести значения этих переменных в (2), то можно увидеть следующее: с= Присвойте это значение(2), чтобы определить скорость год= 1—v0kt• Найти длину пути, по которому корабль прошел за п

ервые 10 секунд?！Используйте клавиши со стрелками для перемещения. Зависимость ДС _ ВН При объединении переменных в изоляции можно увидеть следующее: ДС = Откуда? Ю. Ю. _ dvnt _ _ К-Д (- подойдя к） > Я-vjtt ЮА л-КВ * Т Так… 10. 5 = — Ifl (1-kv0t） При замене значений для всех величин, вы получите следующее: ы = 1200 в(1 + 1 / 1200-15-10) = 1200 в 9/8 ^ 150 м П

осле этого угол окружности в радианах выглядит так О = З / Р = 150/200 = 0.75. Задача 3.44.Движутся линейно с ускорением Вт = 6 Дж Где находится координата point. At время tx = 2 секунды, координаты точек равны lg | = 27 м, скорость равна = 27 м \с Уравнение движения точки и определяет временную зависимость скорости и ускорения. The solution. To найти уравнение движения точки, заданная зависимость ускорения от нуги выражается в виде: Умножьте обе стороны уравнения на dx, чтобы разделить переменные ДХ-ДВ _ я Р-и-Т =-6 WX с дх、 Откуда? ВК-IV—(QX в] / 3

ДХ. При интеграции вы увидите следующее: £°* 4 / 3_С»(1） C — любой Интеграл constant. To определив его, подставим значение m> 1 = 27 м / с в уравнение (1) с^ = 27 м. Затем получим C,= 0 из Формулы (1)、 в = 3х’2 / 3. (2） Используйте зависимость v == dx / dt и умножьте уравнение (2) на dt, чтобы разделить переменные = 3 ДТ. Х2’3. т. Да.） б.） К выпуску 3.35. При интеграции вы увидите следующее: Bx1l = В4-с *(3） Используя условие задачи, опр

еделим произвольную интегральную постоянную: for = 2 sec ^ 1 = 27 m. подставляя эти значения В Уравнении (3) Найти C9 = 3.Получим уравнение движения для точки и подставим значение любой константы в (3).* = Ф Г5 я Подавите значение ego выражения(1) и после простого пр

еобразования уменьшите обе стороны уравнения на tgp. м ^ у-Гуш). Задача 3.38.MAPIC также представляет зависимость величины быстрого ввода или времени от 2 линейно движущихся точек, появляющихся одновременно из одного и того же места. Временная зависимость модуля скорости рисуется на графике первой точки линии, проходящей через начало координат, вторая точка-окружность. И так далее. Определение: 1) у

скорение 2-й точки как функция времени. 2) ускорение первой точки, если мы знаем, что первая догонит вторую точку и второй момент, который остановит гомосексуалиста в конце. 3) Расчет времени К выпуску 3.38. Начало доения до того момента, когда скорость обеих точек будет равна. считайте, что v0 и tt известны. Решение. Рассмотрим любое положение 2-й точки АФ, которое занимает в некоторой точке Т(рис.6). 1.Отрезок MN равен коэффициенту скорости vly во 2-й точке, а отрезок ON соответствует времени t. радиус OM, с одной стороны, равен начальной скорости vQ>2-й точки, А с другой стороны, времени tu, в которое о

станавливается 2-я точка. И затем… В. ® т. что-то, грех=. во-Г1 если упорядочить и добавить в квадрат 2 уравнения Эгиды, то можно увидеть следующее: Ту \ 4、/ / Поэтому коэффициент скорости 2-й точки в любой момент времени равен Проекция ускорения 2-й точки, которая движется по прямой, направление движения выглядит следующим образом. = я)

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

источники:

http://k-a-t.ru/tex_mex/12-kinematika_skor_uskor/index.shtml

http://lfirmal.com/skorost-i-uskorenie-tochki/