«кафедра медицинской и биологической физики И.А. Голёнова ОСНОВЫ МЕДИЦИНСКОЙ СТАТИСТИКИ С ЭЛЕМЕНТАМИ ВЫСШЕЙ МАТЕМАТИКИ Рекомендовано учебно-методическим объединением по . »
Министерство здравоохранения Республики Беларусь
УО «Витебский государственный медицинский университет»
кафедра медицинской и биологической физики
ОСНОВЫ МЕДИЦИНСКОЙ
СТАТИСТИКИ
С ЭЛЕМЕНТАМИ ВЫСШЕЙ МАТЕМАТИКИ
Рекомендовано учебно-методическим объединением по
медицинскому, фармацевтическому образованию в качестве
пособия для студентов учреждений высшего образования, обучающихся по специальности 1-79 01 08 «Фармация»
Витебск – 2017 УДК 61+31(072) ББК 51.1(4Беи),02я73+22.11я73 Г60 Рекомендовано к изданию Центральным учебно-методическим советом ВГМУ (протокол №8 от 21 сентября 2016 г.)
Рецензенты:
кафедра теории функций Белорусского государственного университета Джежора А.А. – заведующий кафедрой математики и информационных технологий УО «Витебский государственный технологический университет», доктор технических наук, доцент;
Г60 Основы медицинской статистики с элементами высшей математики: пособие / И.А. Голёнова.– Витебск: ВГМУ, 2017. – 362 с .
ISBN 978-958-466-855-0 Пособие подготовлено в соответствии с типовой учебной программой по основам медицинской статистики для студентов фармацевтических факультетов. В нем изложены основные вопросы высшей математики, теории вероятностей и статистики, необходимые для решения прикладных задач физики, химии, фармации, биологии и медицины. Приводятся вопросы и задачи для самоконтроля. Пособие предназначено для студентов первого курса фармацевтического факультета, может быть полезно преподавателям и студентам лечебного и стоматологического факультетов .
УДК 61+31(072) ББК 51.1(4Беи),02я73+22.11я73 © Голёнова И.А, 2017 ISBN 978-958-466-855-0 © УО «Витебский государственный медицинский университет»,
СОДЕРЖАНИЕ
ЧАСТЬ I
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА И
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Глава I Производная функции. Дифференциал функции Функциональная связь. Предел функции……………. … § 1.1. 10 Понятие производной функции. Механический и геометрический смысл производной…………………. …… 13 Основные правила дифференцирования функций……… § 1.3. 17 Дифференциал функции…………………………………. .
Функциональная, статистическая и корреляционная зависимости. Уравнение линейной регрессии ……………. 207 Оценка параметров линейной регрессии по несгруппированным данным. Метод наименьших квадратов …….. 210
§ 10.1. Понятие о дисперсионном анализе…………….………. 232 § 10.2. Однофакторный дисперсионный анализ при одинаковом числе испытаний на уровнях ……………………….. 234 § 10.3. Однофакторный дисперсионный анализ при неодинаковом числе испытаний на уровнях …………………….. 237 § 10.4. Понятие о двухфакторном и многофакторном анализах 240
§ 11.1. Виды временных рядов и их характеристики ………….. 251 § 11.2. Отыскание тренда временного ряда …………………… 253 § 11.3. Сглаживание временных рядов: метод скользящего среднего, экспоненциальное сглаживание ……………. 259 § 11.4. Прогнозирование временных рядов ……………………. 265
ПРЕДИСЛОВИЕ
Целью математической подготовки студентов фармацевтических факультетов медицинских университетов является ознакомление их с основными понятиями и методами современного математического аппарата как средства решения задач физического, химического, биологического и иного характера, встречающихся как в процессе изучения профильных дисциплин, так и в дальнейшей профессиональной деятельности .
Содержание данного пособия соответствует типовой учебной программе по основам медицинской статистики для студентов фармацевтических факультетов медицинских университетов, утвержденной МО РБ в 2014 г .
Пособие состоит из четырех частей: «Элементы математического анализа и дифференциальных уравнений», «Элементы теории вероятностей», «Математическая статистика», «Методы оптимизации и управления в фармации». Наряду с классическими разделами подробно представлены такие новые и весьма актуальные разделы, как непараметрические критерии, временные ряды и др. В пособии описаны этапы планирования медицинского исследования, проверки статистических гипотез, а также основные методики и алгоритмы математической статистики, применяемые в научных исследованиях, практическом здравоохранении и фармации .
Каждая глава включает теоретический материал, подробно разобранные примеры решения задач, вопросы для самоконтроля и задания для самостоятельного решения. В конце учебного пособия приведен глоссарий основных математических терминов, список литературы и приложения, содержащие некоторые справочные формулы и таблицы .
В отличие от аналогичных изданий по статистике, в данном пособии, при изложении теоретической части материала, основной акцент сделан не на строгих математических доказательствах соответствующих теорем, а на их смысле и возможностях практического применения в медицине и фармации, что имеет особое значение для студентов медицинских специальностей. В связи с профессиональной направленностью обучения, помимо элементов высшей математики, теории вероятностей и статистики, во всех главах приведены примеры и задачи из области физики, химии, биологии, медицины и фармации .
Материалы учебного пособия могут быть также использованы студентами лечебного и стоматологического факультетов при изучении отдельных тем курса «Медицинская и биологическая физика», студентами фармацевтического факультета заочной формы обучения, аспирантами и магистрантами при выполнении исследования .
§ 1.1. Функциональная связь. Предел функции Функцией или отображением множества X в множество Y называют правило, по которому каждому элементу x X ставится в соответствие определенный элемент y Y. При этом используется запись y = f (x). Переменная x называется независимой переменной или аргументом, а переменная y называется зависимой переменной (от x ) или функцией .
Множество X называют областью определения функции и обозначают D ( f ), а множество Y – областью значений функции и обозначают E ( f ) .
2. Табличный способ – это задание функции с помощью таблицы .
Табличный способ задания функции широко используется в экспериментальных исследованиях и наблюдениях.
Например, измеряя температуру тела больного через определенные промежутки времени, можно составить таблицу значений температуры тела t как функции времени :
Недостатком табличного способа является то, что функция задается не для всех значений аргумента .
3. Графический способ – это задание функции в виде графика .
Графиком функции y = f ( x ) называется изображение на координатной плоскости множества пар ( x, y ) (рис. 1.1) .
Многие приборы, применяемые в медицине и фармации, записывают непосредственно на бумаге или на экране электронно-лучевой трубки результат исследования в виде графика. Так, с помощью электрокардиографа на пленке фиксируется величина возникающих при сокращении сердечной мышцы биопотенциалов U как функция времени t. Преимуществом геометрического способа задания функции по сравнению с аналитическим и табличным является его наглядность .
Рис.1.1
Если для любых значений аргументов x1, x2 D ( f ) из неравенства x1 x2 вытекает неравенство f ( x1 ) f ( x2 ), то функция называется возрастающей на множестве D ( f ) .
Если для любых значений аргументов x1, x2 D ( f ) из неравенства x1 x2 вытекает неравенство f ( x1 ) f ( x2 ), то функция называется неубывающей на множестве D ( f ) .
Если для любых значений аргументов x1, x2 D ( f ) из неравенства x1 x2 вытекает неравенство f ( x1 ) f ( x2 ), то функция называется убывающей на множестве D ( f ) .
Если для любых значений аргументов x1, x2 D ( f ) из неравенства x1 x2 вытекает неравенство f ( x1 ) f ( x2 ), то функция называется невозрастающей на множестве D ( f ) .
Возрастающие, невозрастающие, убывающие и неубывающие функции на множестве D ( f ) называются монотонными на этом множестве, а возрастающие и убывающие – строго монотонными. Интервалы, в которых функция монотонна, называются интервалами монотонности .
Предел функции
Пусть функция f ( x ) определена в некоторой окрестности точки x0, за исключением, быть может, самой точки x0. Число A называют пределом функции f ( x ) в точке x0, если для любого положительного, как бы мало оно не было, найдется такое положительное число, что для любого x x0, удовлетворяющего неравенству x x0, выполняется соотношение f ( x) A .
То, что функция f ( x ) в точке x0 имеет предел, равный A, обозначают следующим образом:
x x0 Геометрически существование предела означает, что для любой
-окрестности точки A найдется такая -окрестность точки x0, что для всех x x0 из этой -окрестности соответствующие точки графика f ( x ) лежат внутри полосы шириной 2, ограниченной прямыми y = A и y = A + (рис. 1.2) .
Рис.1.2
Замечание. На рис. 1.2 функция y = f ( x ) в точке x = x0 имеет предел, равный A, но значение функции f ( x0 ) A, т.е. функция y = f ( x ) разрывна в точке x0 .
Таким образом, понятие предела функции дает возможность ответить на вопрос, к чему стремятся значения функции, когда, когда значения аргумента приближаются к x0 .
Непрерывность функции
Рассмотрим функцию y = f ( x ), определенную в интервале (a, b) .
Пусть x0 и x – два произвольных значения независимой переменной из области определения функции. Тогда x x0 = x называется приращением независимой переменной (или приращением аргумента), следовательно x x0 = x. Приращением y функции y = f ( x ), соответствующим приращению x аргумента x в точке x0, называется разность y = f ( x0 + x) f ( x0 ) .
Функция y = f ( x ) называется непрерывной в точке x0, если бесконечно малому приращению x аргумента x в точке x0 соответствует бесконечно малое приращение функции y, т.е .
lim y = lim [ f ( x0 + x) f ( x0 )] = 0 .
x 0 x 0 Другими словами, функция y = f ( x ) непрерывна в точке x0, если lim f ( x) = f ( x0 ), т.е. предел функции в точке x0 равен значению функx x0 ции в этой точке .
Задача о скорости движущейся точки. Пусть материальная точка М движется вдоль некоторой прямой. Уравнение S = S (t ) выражает путь S, пройденный точкой, как функцию времени t. Это равенство называют законом прямолинейного движения материальной точки. Требуется найти скорость движения точки .
Если в некоторый момент времени t точка занимает положение М, то в момент времени t + t ( t – приращение времени) точка займет положение N, где ON = S (t ) + S (t ) ( S (t ) – приращение расстояния) (рис. 1.3). Таким образом, перемещение точки М за время t будет S (t ) = S (t + t ) S (t ) .
Нахождение производной функции с использованием общего правила дифференцирования весьма трудоемкий и сложный процесс. Поэтому из общего правила дифференцирования выводят ряд формул дифференцирования, полагая, что все рассматриваемые функции имеют производную при заданном значении аргумента .
Производная постоянной величины равна нулю:
(С ) = 0, где С = const .
Производная суммы. Пусть u (x) и v(x) – две дифференцируемые функции, определённые на одном и том же промежутке.
Тогда производная алгебраической суммы этих функций равна алгебраической сумме производных этих функций:
(u ( x) + v( x))’ = u( x) + v’ ( x) .
Методом математической индукции доказывается, что эта формула справедлива для любого конечного числа слагаемых:
(u1 + u2 +. + uk )’ = u ‘1 +u ‘2 +. + u ‘k .
Пример 1.3 .
Вычислить производную функции f ( x) = x + sin x Решение .
f ( x) = ( x + sin x) = ( x) + (sin x) = 1 + cos x .
Все функции, которые изучаются в школьном курсе математики, называются основными элементарными функциями. К ним относятся: степенная, показательная, логарифмическая, тригонометрическая и обратная тригонометрическая функции .
Таблица основных формул дифференцирования функций
§ 1.5. Производные и дифференциалы высших порядков Производная y = f (x) данной дифференцируемой функции y = f (x), называемая производной первого порядка, представляет собой некоторую новую функцию. Возможно, что эта функция сама имеет производную. Тогда производная от производной первого порядка называется производной второго порядка или второй производной и обозначается так: y = ( y) или f (x). Аналогично если существует производная от производной второго порядка, то она называется производной третьего порядка или третьей производной и обозначается так: y = ( y) или f (x) и т. д .
Производная от (n 1) производной (n – натуральное число) называется производной n-ого порядка или n-ой производной и обозначается ( y ( n 1) ) = y ( n ) .
Пример 1.9 .
Найти производную третьего порядка функции y = 2 x3 3x 2 + 1 .
Вычислим производную первого порядка для заданной функции:
y = (2 x3 3 x 2 + 1) = 6 x 2 6 x .
Найдем производную второго порядка:
y = ( y) = (6 x 2 6 x) = 12 x 6 .
Аналогично вычислим производную третьего порядка:
y = ( y) = (12 x 6) = 12 .
Пусть S = S (t ) – уравнение прямолинейного движения материальной точки. Мгновенная скорость v(t ) также как и закон движения, является функцией времени. Поэтому можно рассматривать вторую производную от закона движения как скорость изменения скорости, или вторую производную от функции закона движения: v(t ) = S (t ) = a. В физике данная величина называется ускорением и, также как и скорость, имеет важное значение для исследования различных процессов .
Таким образом, физический (или механический) смысл второй производной заключается в следующем: если задан закон, которому подчиняется движение материальной точки, то вторая производная есть ускорение этого движения .
§ 1.6. Функции нескольких переменных .
Частные производные и дифференциалы Большинство процессов, явлений в окружающем нас мире определяются не одной независимой переменной, а несколькими, функционально связанными между собой. Для изучения подобных зависимостей введено понятие функции нескольких переменных .
Например, площадь прямоугольника S = ab есть функция двух независимых переменных сторон a и b. Объем прямоугольного параллелепипеда V = abc является функцией трех независимых переменных – ребер a, b, c параллелепипеда .
Переменная z называется функцией двух независимых переменных x и y, если некоторым парам значений x и y по какомулибо правилу или закону ставится в соответствие определенное значение z. Символически функция двух переменных обозначается так:
1. Какие задачи приводят к понятию производной?
2. Что называется производной функции?
3. Какая математическая операция называется дифференцированием?
4. Что изучает дифференциальное исчисление?
5. Назовите условие непрерывности функции. Сформулируйте соответствующую теорему .
6. В чём заключается механический (физический) смысл производной?
7. Охарактеризуйте геометрический смысл производной. Ответ подкрепите соответствующими формулами и графиком .
8. Как вычисляется производная по её определению?
9. Сформулируйте и запишите основные теоремы о вычислении производной .
10. Какая функция называется сложной?
11. Как вычисляется производная сложной функции?
12. Что называется производными высших порядков? Какой смысл они имеют?
13. Сформулируйте механический (физический) смысл производной второго порядка .
14. Что называется дифференциалом функции?
15. Как дифференциал функции связан с приращением функции?
16. Можно ли применять дифференциал к приближенным вычислениям?
17. Что называется функцией нескольких аргументов?
18. Что называется частной производной функции нескольких переменных?
19. Что называется частной производной второго порядка? Запишите соответствующие формулы .
20. В чем суть смешанной производной второго порядка?
21. Что называется частным дифференциалом функции нескольких переменных?
22. Что называется полным дифференциалом функции?
23. Что такое абсолютная ошибка измерений?
47. Зависимость между количеством х вещества, полученного в некоторой химической реакции, и временем t выражается уравнением x = A(1 + e k t ), где А и k – постоянные. Вычислить скорость реакции .
48. Растворение лекарственных веществ из таблеток подчиняется уравнению c = c0e k t, где с – количество лекарственного вещества в таблетке, оставшееся к времени растворения, c0 – исходное количество лекарственного вещества в таблетке; k – постоянная скорости растворения. Вычислить скорость растворения лекарственных веществ из таблеток .
49. Смещение тканей в ответ на одиночное мышечное сокращение (единичный импульс) описывается уравнением y = te t / 2, t 0. Вычислить скорость и ускорение в зависимости от времени .
50. Рост числа бактерий подчиняется закону f (t ) = .
1 + 0,1(et 1) Вычислить скорость роста числа бактерий .
51. Форму комплекса потенциалов, возникающих при возбуждении сетчатки глаза светом (электроретинограмма), можно выразить уравнением u = r sin( 3,05 103 t 3 + 5,6 102 t 2 + 1,59 101t ), где r – постоянная, t – время. Вычислить скорость изменения потенциала в начальный момент времени t = 0 .
52. Для увеличения сокоотдачи при обработке свежего лекарственного растительного сырья используется ультразвук. Общее уравнение сокоотдачи при использовании ультразвука имеет вид y = A(1 + kt 0,7e 0,01425 h ), где A, k – постоянные, t – продолжительность процесса, h – толщина озвучиваемого слоя сырья. Записать уравнения скорости сокоотдачи: 1) для h = const ; 2) для t = const .
53. Скорость химической реакции под действием ультразвука 2E определяется формулой v = A, где A – постоянная, E – звуковая Vt энергия, поглощенная в объеме V за время t. Записать уравнение скорости v химической реакции для E = BV sin 2 t, где B и – постоянные .
54. При лечении некоторых заболеваний одновременно назначаются два препарата. Реакция организма (например, понижение температуры) на дозу x первого препарата и дозу y второго препарата описывается зависимостью f ( x, y ) = x 2 y 2 (a x)(b y ), где a, b – постоянные .
Определить дозу y второго препарата, которая вызовет максимальную реакцию при фиксированной дозе x первого препарата .
55. Реакция организма на дозу лекарственного препарата спустя t часов после приема описывается зависимостью f ( x, t ) = x 2 (a x)t 2e t .
При какой дозе x реакция организма окажется максимальной и когда она наступит?
§ 2.1. Первообразная функции и неопределенный интеграл Известно, что многие математические операции образуют пары взаимно обратных действий. Например, сложение и вычитание, умножение и деление, логарифмирование и потенцирование. Точно также и для операции дифференцирования существует обратная операция – интегрирование или нахождение функции F (x) по известной ее производной f ( x) = F ( x) или дифференциалу f ( x)dx. Функцию F (x) называют первообразной на заданном промежутке для функции f (x), если для всех х из этого промежутка F ( x) = f ( x) или dF ( x) = f ( x)dx .
Например, функция F ( x) = x 2 есть первообразная для функции f ( x) = 2 x на промежутке (; + ), т. к. F ( x) = ( x 2 ) = 2 x = f ( x) для всех x (; + ). Можно заметить, что функция x 2 + 6 имеет ту же самую производную 2 x ; поэтому x 2 + 6 также есть первообразная для f ( x) = 2 x на всей области определения. Ясно, что вместо «6» можно поставить любую постоянную «С». Таким образом, задача нахождения первообразной неоднозначна. Она имеет бесконечное множество решений .
Совокупность всех первообразных F ( x) + C для данной функции f ( x)dx называют неопределённым интегралом от функции f (x) и обозначают f ( x)dx :
f ( x)dx = F ( x) + C
– читается «неопределенный интеграл эф от икс дэ икс», где f ( x)dx – подынтегральное выражение; f (x) – подынтегральная функция; С – постоянная интегрирования; символ – знак неопределенного интеграла. Под знаком неопределенного интеграла мы имеем не производную искомой функции, а ее дифференциал .
Вычисление интеграла от данной функции называется интегрированием этой функции .
Понятие определенного интеграла широко используется в математике и в различных прикладных науках. Например, при вычислении площадей фигур, ограниченных кривыми, объемов тел произвольной формы, работы переменной силы, и т. д. В свою очередь, задача вычисления площади криволинейной трапеции приводит к определению понятия определенного интеграла .
Пусть имеется непрерывная функция y = f (x) на отрезке [a; b] .
Фигура, ограниченная данной кривой y = f (x), отрезком [a; b] оси абсцисс и прямыми x = а и y = b, называется криволинейной трапецией (рис. 2.1) .
a Таким образом, нахождение определённого интеграла сводится к следующим операциям:
1) находят первообразную для данной функции;
2) вычисляют первообразную для данных частных значений верхнего и нижнего пределов интегрирования (подставляют пределы интегрирования в первообразную вместо х);
3) находят разность частных значений первообразной F (b) F (a ) .
Пример 2.4 .
Вычислить интеграл x3dx .
x 4 3 34 24 81 16 x dx = 4 |2 = 4 4 = 4 4 = 20,25 4 = 16,25 .
Как и для неопределённого интеграла, этот метод называется методом непосредственного интегрирования. Он применим для наиболее простых функций и использует первообразные, которые есть в таблице неопределенных интегралов. Если же интегрируемая функция является сложной, и её непосредственно проинтегрировать не получается, то применяют другие методы, например, метод замены переменной .
Рассмотрим пример, когда тело движется по прямой MN под действием переменной силы F = f (s ) (рис. 2.3). Направление силы совпадает с направлением движения. Требуется вычислить работу, производимую силой F = f (s ) при перемещении тела из положения M и положение N .
1. Какое действие называется интегрированием?
2. Какую функцию называют первообразной для данной функции f (x) ?
3. Сколько первообразных может существовать для каждой функции?
Чем отличаются друг от друга эти первообразные?
4. Что называется неопределённым интегралом?
5. Что значит проинтегрировать функцию?
6. Каким действием проверяется результат интегрирования?
7. Какими свойствами обладает неопределённый интеграл?
8. Указать известные методы вычисления неопределённых интегралов?
9. Правила нахождения неопределённых интегралов методом непосредственного интегрирования .
10. Правила нахождения неопределённого интеграла методом замены переменных (методом подстановки) .
11. Правила нахождения неопределённого интеграла методом интегрирования по частям .
12. Что называется криволинейной трапецией?
13. Что такое интегральная сумма?
14. Что называется определённым интегралом?
В чём заключается геометрический смысл определённого интеграла?
15. Свойства определенного интеграла .
16. Что называется определённым интегралом с переменным верхним пределом?
17. Какая связь существует между неопределенным и определенным интегралом? Запишите соответствующую формулу .
18. Какие Вам известны методы вычисления определённых интегралов?
19. Правила нахождения определённого интеграла методом замены переменных (методом подстановки) .
20. Правила нахождения определённого интеграла методом интегрирования по частям .
41. Скорость укорочения мышцы описывается уравнением dx = B( x0 x), где х0 – полное укорочение мышцы; х – укорочение dt мышцы в данный момент; В – постоянная, зависящая от нагрузки. Записать закон сокращения мышцы x = x(t ), если в момент времени t = 0 укорочение мышцы было равно нулю .
42. Скорость движения кисти руки задана уравнением v = t 2 + 3 (см / с). Найти уравнение движения кисти, если за первые 6 секунд было пройдено 40 см .
43. Угловая скорость вращения барабана кимографа = 6t 4t + 5. Найти угол поворота, если за t = 2 c был совершен поворот на = 2 рад .
44. Скорость распада радиоактивного вещества v = km0e k t, где k – постоянная, m0 – масса радиоактивного вещества при t = t0. Составить уравнение изменения массы m(t ) .
45. Скорость растворения лекарственного вещества из таблетки v = с0 k F e k F t, где c0 – концентрация лекарственного вещества при t = 0, k – постоянная растворения, F – площадь поверхности растворяемого вещества в единице объема. Составить уравнение растворения лекарственного вещества, если при t = 0 с = сs c0, где сs – концентрация насыщения .
46. Вычислить площадь фигуры, заключенной между кривой y = sin x и осью Ох, в пределах от 0 до .
47. Вычислить площадь фигуры, заключенной между кривыми y1 = x3 и y2 = 4 x .
48. Вычислить площадь фигуры, ограниченной параболой y = x 2 + 2 и прямой x + y = 4 .
49. Пользуясь методом интегрирования, вычислить площадь круга x + y2 = R2 .
50. Вычислить силу давления воды на стенку аквариума с основанием 1,8 м и высотой 0,6 м .
51. Через участок тела животного проходит импульс тока, который изменяется с течением времени по закону J = 20e 5t (мА). Длительность импульса 0,1 с. Вычислить работу, совершаемую током за это время, если сопротивление участка 20 кОм .
52. Найти работу при растяжении мышцы на 4 см, если для ее растяжения на 1 см требуется нагрузка 10 Н. Считать, что сила, необходимая для растяжения мышц, пропорциональна ее удлинению .
53. Через участок тела животного проходит импульс тока, который изменяется с течением времени по закону J = 10 e 3t (мА). Длительность импульса 0,1 с. Вычислить заряд, протекающий через тело животного .
54. Вычислить работу, произведенную при сжатии пружины на 0,03м, если известно, что для укорочения ее на 0,005 м нужно приложить силу в 10 Н .
55. Реакция организма на определенную дозу лекарственного препарата f (t ) = 1 /(1 + t 2 ) в момент времени t. Вычислить суммарную реакцию на данную дозу .
ет его в тождество. Решение, заданное в неявной форме f ( x, y ) = 0, называют интегралом дифференциального уравнения .
Решить уравнение или, как говорят, проинтегрировать его – это значит найти его общее решение .
Общим решением дифференциального уравнения n-го порядка называется функция y = f ( x, C1, C2. Cn ) от x с произвольными постоянными C1, C2. Cn обращающая это уравнение в тождество .
Решение, которое получается из общего решения при некоторых фиксированных значениях произвольных постоянных С, называется частным решением .
При этом задаются не сами постоянные, а условие, которому должно удовлетворять искомое частное решение.
Задание таких условий называется заданием начальных условий и кратко записывается так:
при x = x0, f ( x0 ) = y0, f ( x0 ) = y0 и т.д .
Задача нахождения частного решения, удовлетворяющего начальным условиям, называется задачей Коши .
К сожалению, для многих типов дифференциальных уравнений решение можно найти далеко не всегда. Это является сложнейшей математической задачей. Однако для некоторых типов дифференциальных уравнений решение находится сравнительно легко. К таким уравнениям относятся линейные и некоторые другие типы дифференциальных уравнений 1-го порядка, линейные дифференциальные уравнения с постоянными коэффициентами (любого порядка) .
1. Производные y, входящие в уравнения, необходимо записать в dy виде дроби .
2. С помощью алгебраических операций преобразовать уравнение так, чтобы члены, содержащие y, находились в левой части равенства, а члены, содержащие x, в правой .
3. Проинтегрировать полученное равенство в соответствии с правилами вычисления интегралов. При этом левая часть интегрируется по аргументу y, а правая по аргументу x. Постоянная интегрирования С добавляется в правую часть равенства после вычисления интеграла по x .
4. Полученное после интегрирования уравнение решается относительно y (если это возможно) и находится общее решение .
5. Подставляя в общее решение, значения x и y из начальных (дополнительных) условий, находят значение постоянной С и вид частного решения .
§ 3.3. Однородные дифференциальные уравнения первого порядка
Дифференциальное уравнение вида F ( x, y, y, у) = 0, в которое входит вторая производная неизвестной функции y = f (x), называют дифференциальным уравнением второго порядка .
Рассмотрим уравнения второго порядка, которые могут быть записаны в виде, разрешенном относительно второй производной:
При некоторых ограничениях дифференциальное уравнение второго порядка y = f ( x, y, y) имеет общее решение y = ( x, C1, C2 ), содержащее две произвольные постоянные .
Рассмотрим некоторые виды дифференциальных уравнений второго порядка, приводимых к дифференциальным уравнениям первого порядка .
Дифференциальные уравнения второго порядка, не содержащие искомой функции и её производной
§ 3.5. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами Уравнение вида: y + py + qy = f (x), где p, q – постоянные коэффициенты, а f(x) – некоторая функция, называют линейными дифференциальными уравнениями второго порядка с постоянными коэффициентами .
Если f ( x) = 0 для всех х, то уравнение y + py + qy = 0 называют линейным однородным дифференциальным уравнением (ЛОДУ) второго порядка с постоянными коэффициентами .
Решение такого дифференциального уравнения, как показал Эйлер, следует искать в виде следующих функций: y = e kx, где k – некоторый коэффициент. Подставим значения y = ke kx и y = k 2e kx, найденные из этой функции в уравнение. Тогда получим:
k e + pke + qe = 0 или e (k + pk + q ) = 0 .
2 kx kx kx kx 2
§ 3.6. Моделирование задач физико-химического, фармацевтического и медико-биологического содержания с помощью дифференциальных уравнений Дифференциальные уравнения занимают важное место в решении задач физико-химического и медико-биологического содержания. Пользуясь ими, мы устанавливаем связь между переменными величинами, характеризующими данный процесс или явление .
Химическая кинетика занимается изучением механизма процесса и определением скорости, при которой система достигает равновесия .
При определении скорости протекания процесса важно учесть влияние на нее таких факторов, как концентрация, температура, природа растворителя, присутствие катализатора .
В общем случае скорость химической реакции зависит от концентрации реагирующих веществ. Однако скорость реакции может зависеть также от концентрации других веществ не входящих в стехиометрическое уравнение. Уравнение, выражающее зависимость скорости реакции от концентрации каждого вещества, влияющего на скорость, называется кинетическим дифференциальным уравнением реакции. Рассмотрим химические процессы первого, второго и третьего порядка .
Закон размножения бактерий с течением времени Скорость размножения некоторых бактерий пропорциональна количеству бактерий в данный момент. Найти зависимость изменения количества бактерий от времени .
Обозначим количество бактерий, имеющихся в данный момент, через х. Тогда dx = kx, dt где k – коэффициент пропорциональности .
В уравнении = kx разделим переменные и проинтегрируем его:
dt dx dx = k dt ; = k dt ;
x x ln x = kt + ln C ; ln x = ln e kt + ln C .
Потенцируем последнее выражение: x = Ce kt. Полагая, что при t = 0 и x = x0, получим C = x0. Следовательно, x = x0e kt .
Уравнение x = x0e kt выражает закон размножения бактерий с течением времени. Таким образом, при благоприятных условиях увеличение бактерий с течением времени происходит по экспоненциальному закону .
Этот закон представляет интерес не только с теоретической, но и с практической точки зрения. Он говорит о том, что создавая для полезной популяции благоприятные условия, можно очень быстро получить популяцию с большой численностью. Весьма показательна в этом смысле история с пенициллином. Когда был открыт этот антибиотик, грибки, его выделяющие, стали выращивать в наилучших условиях. Их неограниченно подкармливали, следили, чтобы им не было тесно, и, конечно, оберегали от вредных видов. Будущий урожай можно было совершенно точно подсчитать по формуле. Размножаясь в соответствии с экспоненциальным законом, пенициллиновые грибки в короткий срок обеспечили весь мир ценным лекарством .
Экспоненциальному закону размножения подчиняется так называемый «экологический взрыв», когда тот или иной биологический вид, попав в благоприятные условия, за короткий срок достигает большой численности. Для примера можно указать на губительные нашествия полчищ насекомых (саранчи, шелкопряда и др.) или на неожиданные последствия акклиматизации кроликов в Австралии .
1. Какие уравнения называются дифференциальными?
2. Дайте определение обыкновенному дифференциальному уравнению .
Приведите примеры таких уравнений .
3. Какое дифференциальное уравнение называется уравнением в частных производных? Приведите примеры таких уравнений .
4. Что называется порядком дифференциального уравнения? Приведите примеры .
5. Что называется решением дифференциального уравнения?
6. Что называется общим решением дифференциального уравнения?
7. Что называется частным решением дифференциального уравнения?
8. Как от общего решения дифференциального уравнения перейти к его частному решению?
9. В чём заключается задача Коши?
10. Какие дифференциальные уравнения называются уравнениями с разделяющимися переменными?
11. Сформулируйте правила решения дифференциальных уравнений с разделяющимися переменными .
12. Какие дифференциальные уравнения называются однородными дифференциальными уравнениями первого порядка? Приведите примеры таких уравнений .
13. Какие уравнения относятся к дифференциальным уравнениям второго порядка, допускающие понижение порядка? Приведите примеры таких уравнений .
14. Дайте определение дифференциальным уравнениям второго порядка, не содержащим искомой функции и её производной. Приведите примеры .
15. Дайте определение дифференциальным уравнениям второго порядка, не содержащим искомой функции. Приведите примеры .
16. Дайте определение дифференциальным уравнениям второго порядка, не содержащим аргумента. Приведите примеры .
17. Что называется линейным дифференциальным уравнением второго порядка с постоянными коэффициентами? Запишите соответствующую формулу .
18. Какие дифференциальные уравнения называются линейными однородными дифференциальными уравнениями второго порядка с постоянными коэффициентами? Приведите примеры таких уравнений .
19. Что называется характеристическим уравнением? Запишите формулу .
20. Назовите виды решений характеристического уравнения в зависимости от значений его корней. Дайте пояснения по каждому из видов .
21. В чём заключается закон радиоактивного распада .
22. Запишите формулу для закона поглощения света. Дайте пояснения по каждому составляющему данной формулы .
23. Запишите формулу для закона поглощения ионизирующих излучений веществом. Дайте пояснения по каждому составляющему данной формулы .
24. Перечислите прикладные законы химии, в которых используется теория дифференциальных уравнений. Дайте пояснению по каждому из законов .
25. Перечислите основные задачи фармации, биологии, медицины в которых используется теория дифференциальных уравнений. Дайте соответствующие пояснения по каждой из задач .
Найти общие и, где указано, частные решения линейных однородных дифференциальных уравнений второго порядка:
y + 2 y + 2 y = 0 ; y + y + y = 0 ;
y 6 y + 8 y = 0 ; y 7 y + 10 y = 0 ;
y 4 y + 5 y = 0 ; y y = 0 ;
y 6 y + 8 y = 0 при x = 0, y = 0, y = 1 ;
y 2 y + y = 0 при x = 1, y = 0, y = e .
41. Скорость укорочения мышцы описывается уравнением dx = B( x0 x), где х0 – полное укорочение мышцы; В – постоянная, заdt висящая от нагрузки; х – укорочение мышцы в данный момент. Найти закон сокращения мышцы, если в момент времени t = 0 величина укорочения мышцы была равно 0 .
42. В ультрацентрифугах скорость смещения молекул исследуемого полимера в направлении от оси вращения выражается формулой v = b2 x, где b – постоянная величина, характеризующая данный полимер; – угловая скорость вращения центрифуги; х – расстояние от оси вращения до движущейся границы оседающего полимера. Найти уравнение движения границы полимера, если в момент времени t = 0 она находилась на расстоянии 0,5 см от оси вращения .
43. Если первоначально количество фермента равно 1 г, а через 1 час становится равным 1,2 г, то чему оно будет равно через 5 часов после начала брожения? Скорость приросту фермента считать пропорциональной его наличному количеству .
44. Скорости ферментативных каталитических реакций подчиняются следующему уравнению:
k (a x) dx =, dt 1 + k (a x) где х – концентрация продукта в момент времени t; а – начальная концентрация реагента. Найти закон зависимости изменения концентрации продукта от времени .
45. Популяция бактерий увеличивается таким образом, что удельная скорость роста в момент t (час) составляет величину. Допуt стим, что начальной популяции соответствует x(0) = 1000. Какой будет популяция после 4 часов роста? После 12 часов?
46. За 30 дней распалось 50% первоначального количества радиоактивного вещества. Через сколько времени останется 1% от первоначального количества?
47. Вычислить период полураспада радия и радона, если постоянные распада данных веществ соответственно равны 1,354 1011 с 1 и 2,1 106 с 1 .
48. Имеется 1000 относительных единиц радона. Сколько действующих единиц радона останется спустя 1ч? Постоянная распада радона = 2,1 106 с 1 .
49. Скорость растворения лекарственного вещества в таблетках пропорциональна количеству лекарства в таблетке. Известно, что при t = 0, m = m0. Найти закон растворения таблетки (т.е. закон изменения массы), если период полурастворения таблетки Т .
50. В культуре дрожжей быстрота прироста дрожжевого фермента пропорциональна количеству, имеющемуся в наличии. В начальный момент x = x0. Если количество удваивается в течение часа, то во сколько раз оно возрастет за 2,5 часа .
51. Известно, что скорость распада радия пропорциональна его конечному количеству и что половина его первоначального количества распадается в течение 1600 лет. Определить какой процент m0 радия распадется в течение 100 лет, если первоначальное его значение равно m0 .
52. В воде с температурой 30 С в течение 10 минут тело охлаждается от 100С до 40 С. До какой температуры охладится тело за 30 минут, если по закону Ньютона скорость охлаждения пропорциональна разности температур тела и охлаждающей среды?
53. Найдите закон убывания лекарственного препарата в организме человека, если через 1 час после введения 10 мг препарата его масса уменьшилась вдвое. Какое количество препарата останется в организме после двух часов?
54. Уменьшение интенсивности света при прохождении через поглощающее вещество пропорционально интенсивности падающего света и толщине поглощающего слоя. Найдите закон убывания интенсивности света, если известно, что при прохождении слоя l = 0,5 м интенсивность света убывает в 2 раза .
55. Скорость роста числа микроорганизмов пропорциональна их количеству в данный момент. В начальный момент имелось 100 микроорганизмов, и их число удвоилось за 6 часов. Найти зависимость количества микроорганизмов от времени и количество микроорганизмов через сутки .
Теория вероятностей – область математики, изучающая закономерности в случайных явлениях. Случайное явление – это явление, которое при неоднократном воспроизведении одного и того же опыта может протекать каждый раз несколько по-иному .
Очевидно, что в природе нет ни одного явления, в котором не присутствовали бы в той или иной мере элементы случайности, но в различных ситуациях мы учитываем их по-разному. Так, в ряде практических задач ими можно пренебречь и рассматривать вместо реального явления его упрощенную схему – «модель», предполагая, что в данных условиях опыта явление протекает вполне определенным образом. При этом выделяются самые главные, решающие факторы, характеризующие явление. Именно такая схема изучения явлений чаще всего применяется в физике, технике, механике. Именно так выявляется основная закономерность, свойственная данному явлению и дающая возможность предсказать результат опыта по заданным исходным условиям .
Однако описанная классическая схема так называемых точных наук плохо приспособлена для решения многих задач, в которых многочисленные, тесно переплетающиеся между собой случайные факторы играют заметную (часто определяющую) роль. Здесь на первый план выступает случайная природа явления, которой уже нельзя пренебречь .
Это явление необходимо изучать именно с точки зрения закономерностей, присущих ему как случайному явлению. В физике примерами таких явлений служат броуновское движение, радиоактивный распад, ряд квантово-механических процессов и др .
Предмет изучения биологов и медиков – живой организм, зарождение, развитие и существование которого определяется очень многими и разнообразными, часто случайными внешними и внутренними факторами. Именно поэтому явления и события живого мира во многом тоже случайны по своей природе .
Элементы неопределенности, сложности, многопричинности, присущие случайным явлениям, обусловливают необходимость создания специальных математических методов для изучения этих явлений. Разработка таких методов, установление специфических закономерностей, свойственных случайным явлениям, – главные задачи теории вероятностей .
Рассмотрим основные понятия теории вероятностей .
Исходным понятием теории вероятностей является испытание .
Испытанием называется осуществление некоторого определенного комплекса условий, который может быть воспроизведен сколь угодно большое число раз .
Организация одних испытаний зависит от нас самих (например, подбрасывание монеты или игрального кубика, извлечение шаров из ящика), организация других – нет (например, простое наблюдение за средней температурой данного дня года, проводимое в течение многих лет) .
Каждое испытание может привести или не привести к некоторому исходу, результату. Исход испытания называется событием .
Например, стрелок стреляет по мишени, разделенной на четыре области. Выстрел – это испытание. Попадание в определенную область мишени – событие .
Случайным событием называется всякий факт, который в результате опыта (испытания) может произойти или не произойти .
Различные случайные события обозначаются латинскими буквами A, B, C. .
Например, событие A – появление герба при бросании монеты;
событие B – попадание в цель при выстреле; событие C – появление цветного шара при извлечении шаров из ящика .
Случайные события зависят от многих причин, имеющих между собой отдаленную связь, проследить которую мы не можем. Так, при бросании игрального кубика мы не знаем заранее, какая из граней окажется сверху, так как это зависит от очень многих обстоятельств (движения руки, положения игрального кубика в момент броска, особенностей поверхности, на которую падает кубик, и т. д.) .
Виды случайных событий
Пусть производится опыт, который имеет ряд возможных событий (исходов): A, B, C. и т. д .
События A, B, C называются единственно возможными, если в результате каждого испытания хотя бы одно из них обязательно наступит. Говорят также, что рассматриваемые события образуют полную группу событий .
Пример 4.1 .
При бросании игрального кубика единственно возможные события, состоящие в выпадении одного, двух, трех, четырех, пяти и шести очков, образуют полную группу событий .
Два события называются несовместными, если в результате опыта появление одного из них исключает появление другого в одном и том же испытании .
Пример 4.2 .
В ящике находится пять шаров, помеченных номерами: 1, 2, 3, 4, 5. При извлечении шара вскроется только один из пяти номеров, значит, события, состоящие в появлении этого номера при дальнейшем извлечении шаров из ящика, являются несовместными .
Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же испытании .
Пример 4.3 .
При бросании игрального кубика событие A – появление четырех очков, событие B – появление четного числа очков. В этом случае события A и B совместные .
События называются равновозможными (равновероятными), если при испытании не существует никаких объективных причин, вследствие которых одно из них могло бы наступать чаще, чем другое .
Пример 4.4 .
Появление герба или решки при бросании монеты – события равновозможные. Но если в ящике находится восемь белых и два черных шара, то появления белого или черного шара не могут быть событиями равновозможными. Они носят название событий неравновозможных .
Единственно возможные, несовместные и равновозможные события называются случаями .
Два события A и В называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит. Событие, противоположное событию A, обозначают через А .
Пример 4.5 .
Попадание и промах при выстреле по цели – противоположные события. Если A – попадание, то А – промах .
Событие называется достоверным, если в данном испытании оно является единственно возможным его исходом .
Событие называется невозможным, если в данном испытании оно заведомо не может произойти .
Пример 4.6 .
При извлечении шара из урны, в которой все шары белые, событие A – вынут белый шар – достоверное событие; В – вынут черный шар – невозможное событие .
Заметим, что достоверное и невозможное события в данном испытании являются противоположными .
§ 4.2. Классическое и статистическое определение вероятности
Вероятность – одно из основных понятий теории вероятностей .
Существует несколько определений этого понятия .
Рассмотрим пример. Пусть в урне содержится 6 одинаковых, тщательно перемешанных шаров, причем 2 из них – красные, 3 – синие и 1 – белый. Очевидно, возможность вынуть наудачу из урны цветной (т.е. красный или синий) шар больше, чем возможность извлечь белый шар. Можно ли охарактеризовать эту возможность числом? Оказывается, можно. Это число и называют вероятностью события (появления цветного шара). Таким образом, вероятность есть число, характеризующее степень возможности появления события .
Поставим перед собой задачу дать количественную оценку возможности того, что взятый наудачу шар цветной. Появление цветного шара будем рассматривать в качестве события A. Каждый из возможных результатов испытания (испытание состоит в извлечении шара из урны) назовем элементарным исходом (элементарным событием) .
Элементарные исходы обозначим через 1, 2, 3 и т. д. В нашем примере возможны следующие 6 элементарных исходов: 1 – появился белый шар; 2, 3 – появился красный шар; 4, 5, 6 – появился синий шар .
Те элементарные исходы, в которых интересующее нас событие наступает, назовем благоприятствующими этому событию. В нашем примере благоприятствуют событию A (появлению цветного шара) следующие 5 исходов: 2, 3, 4, 5, 6 .
Таким образом, событие A наблюдается, если в испытании наступает один, безразлично какой, из элементарных исходов, благоприятствующих A ; в нашем примере A наблюдается, если наступит 2 или 3 или 4, или 5 или 6 .
Отношение числа благоприятствующих событию А элементарных исходов к их общему числу называют вероятностью события А и обозначают через Р( А). В рассматриваемом примере всего элементарных исходов 6; из них 5 благоприятствуют событию A. Следовательно, вероятность того, что взятый шар окажется цветным, равна Р( А) =. Это число и дает ту количественную оценку степени возможности появления цветного шара, которую мы хотели найти. Дадим теперь определение вероятности .
Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Итак, вероятность события A определяется формулой m P( A) =, n где m – число случаев благоприятствующих появлению события A ; n – общее число всех равновозможных случаев .
Здесь предполагается, что элементарные исходы несовместны, равновозможны и образуют полную группу .
Пример 4.7 .
У кабинета дежурного психотерапевта ожидают приема трое больных. Врачу известно по медицинским карточкам, что один из ожидающих, по фамилии Петров, болел в прошлом маниакальнодепрессивным психозом. Врач интересуется этим больным, но не хочет вне очереди вызывать его в кабинет .
Обозначим как событие A тот факт, что в кабинет врача входит больной Петров; как событие В обозначим то, что входит другой больной – Сидоров и как событие С – входит Иванов. События A, В и С – несовместные и образуют полную группу (предполагается, что к врачу больные входят по одному). Так как появиться согласно очереди может равновероятно любой из больных, то до начала приема вероятность появиться первым в кабинете врача для одного из больных, в том числе и для Петрова, равна .
Пример 4.8 .
Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найдем вероятность того, что набрана нужная цифра .
Обозначим через A событие – набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных элементарных исходов равно 10. Эти исходы несовместны, равновозможны и образуют полную группу. Благоприятствует событию A лишь один исход (нужная цифра лишь одна). Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов P ( A) = .
Из приведенного классического определения вероятности вытекают следующие ее свойства:
Свойство 1. Вероятность достоверного события U равна единице .
Действительно, достоверному событию должны благоприятствовать все n элементарных событий, т.е. m = n, следовательно, n P (U ) = = 1 n Свойство 2. Вероятность невозможного события V равна нулю .
В самом деле, невозможному событию не может благоприятствовать ни одно из элементарных событий, т. е. m = 0, откуда:
n Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей .
При рассмотрении классического определения вероятности предполагалось, что случайные события равновозможны. Обычно о равновозможности случайных событий судят исходя из соображений симметрии. Например, при бросании игрального кубика предполагают, что он имеет форму правильного куба. Однако таких задач на практике встречается очень мало. Поэтому в естественнонаучных и технических вопросах пользуются так называемым статистическим определением вероятности .
Отметим, что теория вероятностей применима только к массовым (не уникальным) случайным явлениям. Практика показывает, что массовые случайные явления обладают свойством устойчивости частоты их появления – отношения числа появлений случайного события к числу испытаний. Примером может служить выпадение герба или цифры при бросании монеты, которое является простым и наглядным испытанием .
Практика человека говорит о том, что при большом числе бросаний примерно в 50% испытаний выпадет герб, а в 50% – цифра. А это уже определенная закономерность. Здесь нас интересует не результат отдельного подбрасывания, а то, что получится после многократных подбрасываний. Этот простой эксперимент может служить моделью для решения других задач. Устойчивость частоты случайного события – это объективное свойство массовых случайных событий реального мира .
Отсутствие устойчивости частоты в сериях испытаний свидетельствует о том, что условия испытаний изменяются .
Допустим, что имеется возможность неограниченного повторения испытаний, в каждом из которых при сохранении неизменных условий отмечается появление или непоявление некоторого события А (бросание монеты, извлечение шара из урны, стрельба по цели) .
Пусть при достаточно большом числе n испытаний интересующее нас событие A произошло m раз .
Число m называется абсолютной частотой (или просто частотой) события A, а отношение m P * ( A) = n называется относительной частотой события А в данной серии испытаний .
Результаты многочисленных опытов и наблюдений помогают заключить: при проведении серий из n испытаний, когда число n сравнительно мало, относительная частота P * ( A) принимает значения, которые могут довольно сильно отличаться друг от друга. Но с увеличением P * ( A) – числа испытаний в сериях – относительная частота P * ( A) приближается к некоторому числу P( A), стабилизируясь возле него и принимая все более устойчивые значения .
Статистическое определение вероятности: вероятностью события A в данном испытании называется число P( A), около которого группируются значения относительной частоты при больших n .
m m Несмотря на внешнее сходство, формулы P( A) = и P * ( A) = n n различны по существу. Первая формула служит для теоретического вычисления вероятности события по заданным условиям опыта. Вторая же – для экспериментального определения частоты события. Чтобы ею воспользоваться, необходим опытный, статистический материал .
Между частотой события и его вероятностью существует некоторая связь: ясно, что более вероятные события происходят чаще, чем маловероятные .
Практически невозможным событием называется событие, вероятность которого весьма близка к нулю, но не равна нулю .
Практически достоверным называется событие, вероятность которого весьма близка к единице, но не равна единице .
С данными понятиями связывается принцип практической уверенности, который формулируется следующим образом: если в некотором испытании вероятность случайного события A достаточно близка к единице, то можно быть практически уверенным в том, что при однократном испытании событие A произойдет. Если в некотором испытании вероятность случайного события A достаточно близка к нулю, то можно быть практически уверенным в том, что при однократном испытании событие A не произойдет .
Теорема сложения вероятностей несовместных событий Суммой или объединением двух событий A и B называется событие C, состоящее в наступлении по крайней мере одного из событий A или B .
Сумма событий обозначается как C = A + B или C = A B .
Суммой любого числа событий A1, A2. An называется событие C, которое состоит в осуществлении хотя бы одного из этих событий .
Например, если из орудия произведены два выстрела и А – попадание при первом выстреле, B – попадание при втором выстреле, то A + B – попадание при первом выстреле, или при втором, или в обоих выстрелах .
Разностью двух событий A и B называется событие C, состоящее в том, что в результате испытания произошло событие A и не произошло событие B .
Разность событий обозначается как C = A B .
Теорема умножения вероятностей независимых событий Для рассмотрения последующих теорем необходимо ввести понятия зависимых и независимых событий .
Событие A называется независимым от события В, если вероятность события A не зависит от того, произошло событие В или нет .
Несколько событий называются независимыми в совокупности, если каждое из них и любая комбинация остальных событий есть события независимые .
Несколько событий называются попарно независимыми, если любые два из этих событий независимы .
Например, если монета брошена 2 раза, вероятность появления герба в первом испытании (событие A ) не зависит от появления или непоявления герба во втором испытании (событие В ). В свою очередь вероятность выпадения герба во втором испытании не зависит от результата первого испытания. Такие события A и В будут независимыми .
Произведением или пересечением (совмещением) двух событий A и B называется событие С, которое состоит в осуществлении и события А и события В .
Произведение событий обозначается как C = A B .
Например, если А – деталь годная, В – деталь окрашенная, то АВ – деталь годна и окрашена .
Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий .
Например, если A, B, C – появление «герба» соответственно в первом, втором и третьем бросаниях монеты, то ABC – выпадение «герба»
во всех трех испытаниях .
Теорема 4.4 .
Вероятность сложного события, состоящего из совпадения двух независимых событий, равна произведению вероятностей этих событий:
P( AB) = P ( A) P ( B ) .
Пример 4.11 .
Вероятность выживания одного организма в течение 30 минут P = 0,7. В пробирке с благоприятными для существования этих организмов условиями находятся только что два родившихся организма. Какова вероятность того, что через 30 минут они будут живы?
Пусть событие A – первый организм жив через 30 мин, событие B – второй организм жив через 30 мин. Будем считать, что между организмами нет внутривидовой конкуренции, т. е. события A и B независимы. Событие, состоящее в том, что оба организма живы, есть событие
AB. Таким образом, искомая вероятность:
P( AB) = P ( A) P ( B ) = 0,7 0,7 = 0,49 .
Вероятность осуществления хотя бы одного события
Теорема сложения вероятностей совместных событий Теорема 4.5. Вероятность суммы двух совместных событий A и
B равна сумме вероятностей этих событий минус вероятность их произведения:
P( A + B) = P( A) + P( B) P( AB) .
Замечание. Если события A и B несовместимы, то их произведение AB есть невозможное событие и, следовательно, P( AB) = 0 .
Пример 4.13 .
Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: P( A) = 0,7 и P( B) = 0,8. Найти вероятность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий .
Очевидно, события A и B совместны и независимы. Поэтому P( A + B) = P( A) + P( B) P( AB) = 0,7 + 0,8 0,7 0,8 = 1,5 0,56 = 0,94 .
Теорема умножения вероятностей зависимых событий .
Событие B называется зависимым от события A, если вероятность события B меняется в зависимости от того, произошло событие A или нет .
Во введении случайное событие определено как событие, которое при осуществлении совокупности условий S может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий S, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события B при дополнительном условии, что произошло событие A .
Вероятность события B, вычисленная при условии, что имело место событие A, называется условной вероятностью события В и обозначается как PA (B) или P( B / A) .
Пример 4.14 .
В урне два белых шара и один черный. Пусть появление белого шара при первом извлечении будет событием A, при втором извлечении – событием B. При первом извлечении шара вероятность события A P( A) =. Шары после извлечения в урну не возвращаются. Найти вероятность события B при условии, что: 1) событие A произошло; 2) событие A не произошло .
1) Если событие A произошло, то условная вероятность события В:
2) Если известно, что событие A не произошло, то условная вероятность события B :
Теорема 4.6 .
Вероятность произведения двух зависимых событий A и B равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие уже наступило:
P( AB) = P ( A) P ( B / A) .
Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:
P( ABC ) = P( A) PA ( B) PAB (C ) .
Заметим, что порядок, в котором расположены события, может быть выбран любым, т. е. безразлично какое событие считать первым, вторым и т. д .
Пример 4.15 .
В терапевтическом отделении больницы 70 % пациентов – женщины, а 21 % – курящие мужчины. Наугад выбирают пациента. Он оказывается мужчиной. Какова вероятность, что он курит?
Пусть событие A означает, что пациент – мужчина, а событие В – что пациент курит. Тогда в силу условия задачи P( A) = 0,3, а P( AB) = 0,21. Поэтому искомая условная вероятность равна P( AB) 0,21 P( B / A) = = = 0,7 .
P( A) 0,3 Пример 4.16. Студент пришел на экзамен, зная лишь 40 из 50 вопросов программы. В билете три вопроса. Найти вероятность того, что студент ответит на первый вопрос билета – событие А, на второй вопрос билета – событие В и на третий вопрос билета – событие С .
Вероятность того, что студент ответит на первый вопрос равна:
P( A) = = Вероятность того, что студент ответит на второй вопрос, вычисленная при условии, что он ответил на первый вопрос, т. е. условная вероятность, равна P( B / A) = .
Вероятность того, что студент ответит на третий вопрос билета в предположении, что он ответил на первый и второй вопрос, т. е. условная вероятность, равна P(C / AB) = = .
Тогда искомая вероятность
Следствием теоремы сложения вероятностей для несовместных событий и теоремы умножения вероятностей для зависимых событий является так называемая формула полной вероятности .
Пусть некоторое событие A может произойти при условии, что появляется одно из несовместных событий A1, A2. An, образующих полную группу событий .
Теорема 4.7 .
Вероятность события A, которое может наступить лишь при условии появления одного из n попарно несовместных событий A1, A2. An, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A :
P( A) = P( A1 ) P( A / A1 ) + P( A2 ) P( A / A2 ) +. + P( An ) P( A / An ) n P( A) = P( Ai ) P( A / Ai ) .
i =1 Формулу называют формулой полной вероятности .
Пример 4.17 .
Даны три одинаковые на вид аптечки. В первой аптечке находится 2 тюбика кодеина и 2 тюбика фталазола, во второй – 4 тюбика кодеина и 2 тюбика фталазола, в третьей 5 тюбиков кодеина и 3 тюбика фталазола. Выбирают наудачу одну из аптечек и вынимают из нее тюбик. Найти вероятность того, что вынутый тюбик будет тюбиком кодеина .
Здесь событие A – появление тюбика кодеина – может произойти с одним из событий: А1 – выбор первой аптечки, А2 – выбор второй аптечки, А3 – выбор третьей аптечки .
Выбор каждой аптечки равновозможен, поэтому P( A1 ) = P( A2 ) = P( A3 ) = Условные вероятности события A при событиях A1, A2 и A3 соответственно равны P ( A / A1 ) = =, P ( A / A2 ) = =, P( A / A3 ) = .
По формуле полной вероятности
Комбинаторика раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них. В более широком понимании комбинаторика – это теория конечных множеств. Комбинаторные методы применяются в теории вероятностей, статистике, экономике, физике, химии, биологии и других науках .
Рассмотрим наиболее употребительные формулы комбинаторики .
Перестановки
Пусть М – некоторое конечное множество, состоящее из n элементов:
Перестановкой называется всякое расположение элементов данного конечного множества, получающееся при некотором упорядочении этого множества .
Упорядочить множество – значит выбрать какой-либо элемент этого множества и назвать его первым, выбрать какой-либо другой элемент и назвать его вторым и т. д., а последний элемент назвать n .
Число перестановок из n элементов равно произведению первых n натуральных чисел, т. е .
Pn = 1 2 3 (n 1)n = n !
Произведение n первых натуральных чисел обозначают через n !
(читается: «эн факториал») .
n != (n 1)!n Пример 4.18. Сколькими способами можно разместить 7 больных в палате, насчитывающей 7 коек .
Число способов равно P7 = 7!= 1 2 3 4 5 6 7 = 5040 .
При практическом применении теории вероятностей особое значение имеют события, связанные с независимыми повторными испытаПеринатальный период охватывает внутриутробное развитие плода, начиная с 28-й недели бере
Теорема Лапласа локальная (в дифференциальной форме) Формула Бернулли позволяет вычислить вероятность того, что событие появится в n испытаниях ровно m раз. При выводе предполагалось, что вероятность появления события в каждом испытании постоянна. Легко видеть, что пользоваться формулой Бернулли при больших значениях n достаточно трудно, так как формула требует выполнения действий над громадными числами .
Естественно возникает вопрос: нельзя ли вычислить интересующую нас вероятность, не прибегая к формуле Бернулли? Оказывается, можно. Локальная теорема Лапласа и дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления события ровно m раз в n испытаниях, если число испытаний достаточно велико .
Заметим, что для частного случая, а именно для p = 1 / 2, асимптотическая формула была найдена в 1730 г. Муавром; в 1783 г. Лаплас обобщил формулу Муавра для произвольного p, отличного от 0 и 1 .
Поэтому теорему, о которой здесь идет речь, иногда называют теоремой Муавра – Лапласа .
Доказательство локальной теоремы Лапласа довольно сложно, поэтому мы приведем лишь формулировку теоремы и примеры, иллюстрирующие ее использование .
Локальная теорема Муавра – Лапласа: Если вероятность наступления некоторого события A в n независимых испытаниях постоянна и отлична от нуля и единицы ( 0 p 1 ), то вероятность Pn (m) того, что в n испытаниях событие А наступит ровно m раз, приближенно равна (тем точнее, чем больше n ) значению функции 1 1 x / 2 1
1. Что изучает теория вероятности?
2. Назовите основные задачи теории вероятностей .
3. Что такое испытание? Приведите примеры .
4. Дайте определение событию. Приведите примеры .
5. Что называют случайным событием? Приведите примеры .
6. Перечислите виды случайных событий .
7. Какое событие называют достоверным? Приведите примеры .
8. Какое событие называют невозможным? Приведите примеры .
9. Какие два события называют несовместными? совместными? Приведите примеры .
10. Какие n событий ( n 2 ) называют несовместными попарно? в совокупности? Приведите примеры .
11. Какие события называют противоположными?
12. Какие действия над событиями вы знаете?
13. Что называется суммой, разностью, произведением событий? Приведите примеры .
14. Что такое вероятность?
15. Приведите классическое определение вероятности .
16. Приведите статистическое определение вероятности .
17. Перечислите основные свойства вероятности .
18. Сформулируйте теоремы сложения вероятностей для совместных и несовместных событий .
19. Какие два события называют независимыми? зависимыми? Приведите примеры .
20. Дайте определение условной вероятности .
21. Какие n событий называют независимыми в совокупности? попарно?
22. Какая существует связь между совместными и зависимыми событиями?
23. Напишите формулу полной вероятности .
24. Что называют сочетанием? размещением? перестановкой?
25. Напишите формулу Байеса. Приведите примеры использования данной формулы .
26. Что называют схемой Бернулли?
27. Напишите формулу Бернулли. В каких случаях можно применять формулу Бернулли?
28. Сформулируйте локальную и интегральную теоремы Лапласа .
29. В каких случаях можно применять локальную теорему Лапласа? интегральную теорему Лапласа?
30. Напишите формулу Пуассона. В каких случаях можно применять формулу Пуассона?
Задания для решения
1. Среди 500 ампул проверенных на герметичность, оказалось 10 ампул с трещинами. Вычислить относительную частоту появления ампул, имеющих трещины .
2. Среди 300 пробирок, изготовленных на автоматической линии, оказалось 15 не отвечающих стандарту. Найти частоту появления стандартных пробирок .
3. Примерно 1 ребенок из 700 рождается с синдромом Дауна. В больнице большого города в год рождается 3500 детей. Каково ожидаемое число новорожденных с синдромом Дауна?
4. В коробке 30 таблеток: 10 красных, 5 желтых, 15 белых. Найти вероятность появления цветной таблетки (т.е. или красной или желтой) .
5. Опухоль – «мишень» разделена на три области. При использовании радионуклидного препарата вероятность поражения первой области равна 0,45; второй – 0,35. Найти вероятность того, что при однократном использовании радионуклид попадет либо в первую, либо во вторую мишень .
6. В коробке имеется 7 желтых и несколько белых таблеток. Какова вероятность извлечь белую таблетку, если вероятность извлечь желтую таблетку равна ? Сколько белых таблеток в коробке?
7. В картотеке имеются истории болезней 8 пациентов. Если наугад взять первую, затем вторую, третью и т.д. истории болезней, то какова вероятность в каждом случае изъятия нужной истории болезни?
Предполагается, что искомая история болезни имеется в картотеке. Рассмотрите 2 варианта: а) взятые истории болезней не возвращаются в картотеку; б) взятые истории болезней каждый раз возвращаются в картотеку и хаотически располагаются в ней .
8. С первого предприятия поступило 200 пробирок, из которых 190 стандартных, а со второго – 300, из которых 280 стандартных. Найти вероятность того, что наудачу взятая пробирка будет стандартной .
9. На тридцати историях болезни написаны 30 двузначных чисел от 1 до 30 (их порядковые номера). Эти истории болезни лежат на полке в случайном порядке. Какова вероятность вынуть историю болезни с номером, кратным 2 или 3?
10. Известно, что в партии из 1000 стандартных ампул с новокаином 400 ампул изготовлено на одном заводе, 350 – на втором и 250 ампул – на третьем. Известны также вероятности 0,75; 0,80; 0,85 того, что ампула окажется без дефекта при изготовлении ее соответственно на первом, втором и третьем заводах. Какова вероятность того, что наугад выбранная из данной партии ампула с новокаином окажется без дефекта?
11. Во время эпидемии в одном из населенных пунктов 60% жителей оказались больными. Из каждых 100 больных 10 требуют срочной медицинской помощи. Найти вероятность того, что любому взятому наугад жителю необходима срочная медицинская помощь .
12. Два автомата производят одинаковые хирургические зажимы .
Производительность первого автомата вдвое больше, чем второго. Первый автомат производит в среднем 60% зажимов отличного качества, а второй – 84%. Наудачу взятый зажим оказался отличного качества .
Найти вероятность того, что он произведен первым автоматом .
13. Три врача независимо друг от друга осмотрели одного и того же больного. Вероятность того, что первый врач допустит ошибку при установлении диагноза, равна 0,01. Для второго и третьего врачей эта вероятность соответственно 0,015 и 0,02. Найти вероятность того, что при осмотре больного хотя бы один из врачей допустит ошибку в диагнозе .
14. Вероятность того, что в течение дня прибор для определения распадаемости таблеток выйдет из строя, равна 0,03. Какова вероятность того, что в течение четырех дней подряд прибор не выйдет из строя?
15. При синтезировании в лабораторных условиях какого-то вещества вероятность взрыва в отдельном опыте р=0,02. Вычислить вероятность того, что: 1) в серии из 10 синтезов взрыв произойдет три раза; 2) взрыва не произойдет .
16. Лечение определенного заболевания дает эффект (выздоровление) в 75% случаев. Оно проводилось шести больным. Какова вероятность того, что: 1) выздоровеют все шестеро; 2) не выздоровеет ни один?
17. Вероятность удачного выполнения сложного химического опыта равна р =. Найти вероятность того, что из 10 испытаний удачными будут два .
18. Операция пересадки кожи дает успех в 40% всех случаев. Пациенту делают пересадку кожи несколько раз подряд до тех пор, пока она не удается. Какова вероятность того, что пересадка окажется успешной: 1) с первой попытки; 2) с третьей попытки?
19. Имеется 1000 медицинских карточек, в которых интересующее нас заболевание встречается 100 раз. Найти вероятность того, что это заболевание встретится в 100 наугад отобранных карточках .
20. Завод медицинского оборудования выпускает 90% фонендоскопов первого сорта и 10% фонендоскопов второго сорта. Наугад выбирают 1000 фонендоскопов. Найти вероятность того, что число фонендоскопов первого сорта будет равно 900 .
21. Завод отправил на аптечный склад 5000 термометров. Вероятность повреждений каждого термометра в пути равна 0,0002. Какова вероятность того, что на аптечный склад прибудет ровно 3 поврежденных термометра?
22. В аптеку поступило 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003 .
Найти вероятность того, что аптека получит разбитых бутылок: 1) ровно две; 2) менее двух; 3) более двух; 4) хотя бы одну .
23. Вероятность заболевания туберкулезом легких в данной местности равна 0,003. Какова вероятность того, что при осмотре 1000 человек будет выявлено трое больных?
24. Пусть вероятность того, что электрокардиограф потребует ремонта в течение гарантийного срока, равна 0,2. Найти вероятность того, что в течение гарантийного срока из шести электрокардиографов: 1) не более одного потребует ремонта; 2) хотя бы один потребует ремонта .
25. Аптечный склад получает лекарственные препараты с трех фармацевтических заводов, причем количество препаратов, поступающих с каждого завода, в среднем одинаково. Для аптечного склада желательно получить очередную партию лекарств с завода №1 либо №2 .
Вычислить вероятность этого события .
26. Имеется три аппарата для изготовления таблеток. Вероятность остановки на протяжении часа составляет: для первого аппарата – 0,2, для второго – 0,15 и для третьего – 0,12. Какова вероятность бесперебойной работы всех трех аппаратов на протяжении одного часа?
27. Вероятность бесперебойной работы двух аппаратов для запаивания ампул на протяжении одного часа составляет: для первого – 0,75;
для второго – 0,8. Какова вероятность того, что оба аппарата будут бесперебойно работать на протяжении двух часов?
28. В партии из 1000 стандартных ампул с новокаином 400 ампул изготовлено на первом заводе, а остальные – на втором. Вероятность того, что без дефекта окажется ампула, изготовленная на первом заводе, равна 0,75, на втором заводе 0,80. Найти вероятность того, что любая наугад взятая ампула окажется без дефекта .
29. В пяти аптечках находится одинаковые по массе и размерам таблетки. В двух – по 6 зеленых и 4 желтых таблеток. (Это аптечка состава А1). В двух других аптечках (состава А2) – по 8 зеленых и 2 желтых таблеток. В одной аптечке (состава А3) – 2 зеленых и 8 желтых таблеток. Наудачу выбирается аптечка и из нее извлекается таблетка, которая оказалась зеленой. Какова вероятность того, что зеленая таблетка извлечена из аптечки первого состава?
30. Одна вакцина формирует иммунитет по отношению к краснухе в 95% случаев. Предположим, что вакцинировались 30% населения и что вероятность заболеть краснухой у вакцинированного человека без иммунитета такая же, как и у невакцинированного. Какова вероятность того, что человек, заболевший краснухой, был вакцинирован?
31. Некоторое заболевание, встречающееся у 5% населения, с трудом поддается диагностике. Один грубый тест на это заболевание дает положительный результат (указывает на наличие заболевания) в 60% случаев, когда пациент действительно болен, и в 30% случаев, когда у пациента этого заболевания нет. Пусть для конкретного пациента этот тест дает положительный результат. Какова вероятность того, что у него есть данное заболевание?
32. Пациенты разбиты на две группы одинаковой численности .
Одна группа придерживалась специальной диеты с высоким содержанием ненасыщенных жиров, а контрольная группа питалась по обычной диете, богатой насыщенными жирами. После 10 лет пребывания на этих диетах возникновение сердечно-сосудистых заболеваний в группах составило соответственно 31% и 48%. Случайно выбранный из обследуемых человек страдает сердечно-сосудистым заболеванием. Какова вероятность того, что он принадлежит к контрольной группе?
33. Установлено, что курящие мужчины в возрасте свыше 40 лет умирают от рака легких в 10 раз чаще, чем некурящие. Предположим, 60% мужчин курят. Найдите вероятность того, что мужчина, умерший от рака легких, был курящим .
34. Установлено, что в среднем один из 700 детей мужского пола рождается с лишней Y-хромосомой и что среди таких детей крайне агрессивное поведение встречается в 20 раз чаще. Опираясь на эти данные, представьте, что у мальчика крайне агрессивное поведение. Какова вероятность того, что ребенок имеет лишнюю Y-хромосому?
35. На одном производстве было установлено, что 3% рабочих являются алкоголиками с показателем прогулов втрое выше, чем у остальных. Если случайно выбранный рабочий отсутствует на работе, то какова вероятность того, что он алкоголик?
В математике величина – это общее название различных количественных характеристик предметов и явлений. Длина, площадь, температура, давление и т.д. – примеры разных величин .
Случайной величиной называется переменная величина, которая в зависимости от исхода испытания случайно принимает одно значение из множества возможных значений .
Существует более строгое формальное математическое определение случайной величины .
Случайной величиной будем называть любую функцию, определенную на пространстве элементарных событий, вместе с информацией о том, с какими вероятностями эта функция принимает свои значения (или интервалы своих значений) .
Примерами случайных величин являются: число больных на приеме у врача, количество рецептов, поступивших в аптеку в течение рабочего дня, продолжительность человеческой жизни и др .
Случайные величины обозначают прописными буквами латинского алфавита X, Y, Z,…, а их возможные значения – соответствующими строчными буквами x, y, z, … Вероятности случайных величин обозначают буквами с соответствующими индексами: P( X = x1 ) = P( x1 ) = P и т.д .
Различают дискретные и непрерывные случайные величины .
Случайная величина называется дискретной, если она принимает только определенные, отдельные друг от друга значения, которые можно установить и перечислить .
Примерами дискретной случайной величины являются:
– число студентов в аудитории;
– цифра, которая появляется на верхней грани при бросании игральной кости, которая может принимать лишь целые значения от 1 до 6;
– относительная частота попадания в цель при 10 выстрелах – ее значения: 0; 0,1; 0,2; …, 1;
– число событий, происходящих за одинаковые промежутки времени: частота пульса, число вызовов скорой помощи за 1 час, количество операций в месяц с летальным исходом и т.д .
Случайная величина называется непрерывной, если она может принимать любые значения внутри определенного интервала, конечного или бесконечного .
К непрерывным случайным величинам относятся, например, масса тела и рост взрослых людей, объем мозга, продолжительность жизни, количественное содержание ферментов у здоровых людей, размеры форменных элементов крови, pH крови и т.д .
Понятие случайной величины играет определяющую роль в современной теории вероятностей, разработавшей специальные приемы перехода от случайных событий к случайным величинам .
Если случайная величина зависит от времени, то можно говорить о случайном процессе .
§ 5.2. Закон распределения дискретной случайной величины Чтобы дать полную характеристику дискретной случайной величины, необходимо указать все ее возможные значения и их вероятности .
Соответствие между возможными значениями дискретной случайной величины и их вероятностями называется законом распределения этой величины .
Обозначим возможные значения случайной величины X через xi, а соответствующие им вероятности – через pi. Тогда закон распределения дискретной случайной величины можно задать тремя способами: в виде таблицы, графика или формулы .
В таблице, которая называется рядом распределения, перечисляются все возможные значения дискретной случайной величины X и соответствующие этим значениям вероятности p :
Графически закон представляется ломаной линией, которую принято называть многоугольником распределения (рис.5.1) .
Рис.5.1 Здесь по оси абсцисс откладывают все возможные значения случайной величины xi, а по оси ординат – соответствующие им вероятности pi. Полученные точки соединяют отрезками прямых .
Аналитически закон выражается формулой.
Например, если вероятность попадания в цель при одном выстреле равна p, то вероятность поражения цели один раз при n выстрелах выражается формулой:
P(n) = nq n 1 p, где q = 1 p – вероятность промаха при одном выстреле .
Пример 5.1 .
В денежной лотерее выпушено 100 билетов. Разыгрывается один выигрыш в 50 рублей и 10 выигрышей по 1 рублю .
Найти закон распределения случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета .
Возможные значения для Х: x1 = 50, x2 = 1, x3 = 0.
Вероятности этих значений:
p1 = = 0,01, p2 = = 0,1, p3 = 1 ( p2 + p1 ) = 1 (0,01 + 0,1) = 0,89 .
Закон распределения выигрыша задан в виде таблицы:
Из этой таблице видно, что мода случайной величины Х равна 2, так как этому значению соответствует наибольшая вероятность P(2) = 0,4 .
При составлении годичного плана потребности населения в какомто лекарственном препарате определяют не ее математическое ожидание, а моду, т.е. месяц, в котором чаще всего требуется данный препарат .
В микробиологии для закона распределения вероятностей появления колонии микроорганизмов в пробах также определяют обычно не математическое ожидание, а моду, т.е. пробу, которой соответствует наибольшая вероятность появления колонии микроорганизмов .
В медицине знание среднего возраста детей, заболевших ангиной, менее интересно, чем знание возраста, в котором чаще всего происходит заболевание (в частности, при решении вопроса о том, где должны быть сосредоточены главные профилактические условия: в школах или дошкольных учреждениях) .
Кроме характеристик положения – средних, типичных значений случайной величины, – употребляется еще ряд характеристик, каждая из которых описывает то или иное свойство распределения .
Характеристики рассеяния – это дисперсия и стандартное отклонение (среднее квадратическое отклонение) .
Дисперсией D( X ) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины Х от ее математического ожидания :
D( X ) = 2 = M (( X µ) 2 ) .
Свойства дисперсии дискретной случайной величины
5. Дисперсия разности двух независимых случайных величин X и
Y равна сумме их дисперсий:
D( X Y ) = D( X ) + D(Y ) .
6. Дисперсия числа появления события A в n независимых испытаниях, в каждом из которых вероятность события A постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании: D( X ) = npq .
Следствие. D ( X ± C ) = D( X ) + D(C ) = D( X ) + 0 = D( X ), где С – постоянная .
Пример 5.4 .
Найти дисперсию случайной величины Z = 4 X + 3, если известно, что дисперсия случайной величины Х равна D( Х ) = 3 .
Используя свойства дисперсии получаем:
D( Z ) = D(4 X + 3) = D(4 X ) + D(3) = 42 D( X ) + 0 = 16 3 = 48 .
Дисперсия характеризует рассеяние, разбросанность значений случайной величины Х относительно ее математического ожидания .
Само слово «дисперсия» означает «рассеяние» .
Однако дисперсия D( X ) имеет размерность квадрата случайной величины, что весьма неудобно при оценке разброса в физических, биологических, медицинских и других приложениях. Поэтому обычно пользуются параметром, размерность которого совпадает с размерностью X. Это – среднее квадратическое (стандартное) отклонение .
Вычислить ее математическое ожидание, дисперсию и среднее квадратическое отклонение .
Сначала находим математическое ожидание случайной величины X :
M ( X ) = 0 0,13 + 1 0,35 + 2 0,35 + 3 0,15 + 4 0,02 = 1,58 .
Далее запишем закон распределения X 2 :
Пусть производится n независимых испытаний, в каждом из которых событие A может появиться, либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна p (следовательно, вероятность непоявления q = 1 p ). Рассмотрим в качестве дискретной случайной величины X число появлений события A в этих испытаниях .
Поставим перед собой задачу: найти закон распределения величины X. Для ее решения требуется определить возможные значения X и их вероятности. Очевидно, событие A в n испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза, …, либо n раз. Таким образом, возможные значения X таковы: x0 = 0, x1 = 1, …, xn = n.
Остается найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли:
Pn ( X ) = Cn p X q n X .
X Данная формула является аналитическим выражением искомого закона распределения .
Биномиальным называют распределение вероятностей, определяемое формулой Бернулли. Закон назван «биномиальным» потому, что правую часть равенства Pn ( X ) = Cn p X q n X можно рассматривать как X
Таким образом, первый член разложения p n определяет вероятность наступления рассматриваемого события n раз в n независимых испытаниях; второй член np n 1q определяет вероятность наступления события n 1 раз;. ; последний член q n определяет вероятность того, что событие не появится ни разу .
Напишем биномиальный закон в виде таблицы:
Математическое ожидание случайной величины, подчиняющейся биномиальному распределению, M ( X ) = np .
Дисперсия случайной величины, подчиняющейся биномиальному закону равна D( X ) = npq .
Среднее квадратическое отклонение: = npq .
Пример 5.7 .
Предполагая одинаковыми вероятности рождения мальчика и девочки, установить закон распределения случайной величины X, которая выражает число мальчиков в семье, имеющей пять детей .
Пусть X – количество мальчиков в семье. Величина X может принимать значения 0,1,2,3,4,5. Найдем вероятности этих значений по формуле Бернулли: Pn(m) = Cn р m q n-m .
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события A равна p. Для определения вероятности k появлений события в этих испытаниях используют формулу Бернулли. Если же n велико, то пользуются асимптотической формулой Лапласа. Однако, эта формула непригодна, если вероятность события мала ( p 0,1 ). В этих случаях ( n велико, p мало) прибегают к асимптотической формуле Пуассона .
Итак, поставим перед собой задачу: найти закон распределения величины X если число испытаний велико, а вероятность события очень мала. Для ее решения требуется определить возможные значения X и их вероятности. Очевидно, событие A в n испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза, …, либо n раз. Таким образом, возможные значения X таковы: x0 = 0, x1 = 1, …, xn = n .
Остается найти вероятности этих возможных значений, воспользовавшись формулой Пуассона (приложение 3):
µ X µ e, где µ = np .
Эта формула выражает закон распределения Пуассона вероятностей массовых ( n велико) редких ( p мало) событий .
Распределение Пуассона (приложение 3) является дискретным и характеризуется только одним параметром – математическим ожиданием µ. Среднее квадратическое отклонение = µ .
§ 5.5. Функция распределения и плотность распределения вероятностей непрерывной случайной величины Для описания реальных величин, зависящих от случая, класса дискретных случайных величин, недостаточно. Действительно, таким величинам, как размеры любых физических объектов, температура, давление, длительность тех или иных биологических процессов неестественно приписывать дискретное множество возможных значений. Напротив, естественно считать, что их возможные значения в принципе могут быть любыми числами в некоторых пределах, т.е. они являются непрерывными величинами .
В отличие от дискретной величины закон распределения непрерывной случайной величины невозможно задать в виде таблицы, в которой были бы перечислены все возможные значения этой величины и их вероятности .
Одним из возможных способов задания непрерывной случайной величины является использование с этой целью соответствующей функции распределения .
Функцией распределения случайной величины X называют функцию F (x), равную вероятности P( X x) того, что случайная величина примет значение X, меньшее x :
F ( x) = P( X x) Функцию распределения иногда называют интегральной функцией распределения или интегральным законом распределения .
Геометрически равенство F ( x) = P( X x) можно истолковать так:
F (x) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси интервалом (, x) (рис. 5.4) Рис. 5.4 Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения. Она существует для всех случайных величин, как дискретных, так и непрерывных .
1. Значения функции распределения принадлежат отрезку [0,1] :
Это свойство вытекает из определения функции распределения как вероятности: вероятность всегда вероятность есть неотрицательное число, не превышающее единицы ( 0 Р 1 ) .
2. Функция распределения является неубывающей функцией, т.е .
из неравенства х2 x1 следует неравенство F ( х2 ) F ( x1 ), P( x1 X x2 ) = F ( x2 ) F ( x1) 0 .
Следствие 1. Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю:
Так, вероятность того, что наугад выбранная таблетка будет иметь массу, в точности равную некоторому фиксированному значению, например 0,20 г, равна нулю .
3. Если возможные значения случайной величины принадлежат интервалу (a, b), то: 1) F ( x) = 0 при x a ; 2) F ( x) = 1 при x b .
Следствие 2. Справедливы равенства:
lim F ( x) = F () = 0 ; lim F ( x) = F (+) = 1 .
x x + Данные свойства позволяют представить, как выглядит график функции распределения непрерывной случайной величины .
График функции распределения непрерывной случайной величины расположен в полосе, ограниченной прямыми линиями y = 0 и y = 1 (первое свойство) .
При возрастании x в интервале (a, b), в котором заключены все возможные значения случайной величины, график «поднимается вверх»
При x a ординаты графика равны нулю; при x b ординаты графика равны единице (третье свойство) .
В общем случае он имеет вид, изображенный на рисунке 5.5 .
Рис. 5.5
Для дискретной случайной величины функция распределения F ( x) = P( X = xi ), где неравенство xi x под знаком суммы указываxi x ет, что суммирование распространяется на все значения xi, меньшие x .
В точках возможных значений дискретной случайной величины X функция распределения меняется скачкообразно, причем величина скачка равна вероятности этого значения .
Пример 5.8. Дан ряд распределения дискретной случайной величины:
График функции распределения вероятностей случайной величины X изображен на рисунке 5.6, концы стрелок указывают на точки, не принадлежащие графику .
Выше непрерывная случайная величина задавалась при помощи функции распределения. Этот способ задания не является единственным. Непрерывную случайную величину иногда можно также задать, используя другую функцию, которую называют плотностью распределения или плотностью вероятности (часто ее называют дифференциальной функцией распределения) .
Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f (x), равную первой производной от интегральной функции распределения:
Из приведенного определения следует, что функция распределения является первообразной для плотности распределения .
Заметим, что для описания распределения вероятностей дискретной случайной величины дифференциальная функция неприменима .
Свойства плотности распределения вероятностей
1. Вероятность того, что непрерывная случайная величина X в результате испытания примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от плотности вероятности, взятому в пределах от а до b:
b P(a X b) = f ( x)dx = F (b) F (a ) .
a Геометрически полученный результат можно истолковать так: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью Ox, кривой распределения f (x) и отрезками прямых x = a и x = b (рис. 5.7). Это следует из геометрического смысла определенного интеграла .
§ 5.7. Равномерное и нормальное распределения случайной величины. Понятие о теореме Ляпунова Равномерное распределение случайной величины
Нормальное распределение случайной величины Нормальный закон распределения (закон Гаусса) играет исключительно важную роль в теории вероятностей. Во-первых, это наиболее часто встречающийся на практике закон распределения непрерывных случайных величин. Во-вторых, он является предельным законом в том смысле, что к нему при определенных условиях приближаются другие законы распределения .
Максимальное значение плотности вероятности, равное 1 0,4, соответствует математическому ожиданию µ = Х ; по мере 2 удаления точки х от µ значение плотности f (x) приближается к нулю (рис. 5.10) .
Величина µ называется также центром рассеяния. Среднее квадратическое отклонение характеризует ширину кривой распределения .
Установим, как влияют параметры µ и на форму кривой Гаусса. При изменении значения µ нормальная кривая не меняется по форме, но сдвигается вдоль оси абсцисс (рис. 5.11). Параметр определяет форму кривой нормального распределения. С возрастанием максимальная ордината кривой убывает, а сама кривая, становясь более пологой, растягивается вдоль оси абсцисс; при уменьшении кривая вытягивается вверх, одновременно сжимаясь с боков. Вид кривой распределения при разных значениях (1 2 3 ) показан на рисунке 5.12 .
Рис. 5.11 Рис. 5.12
Рис. 5.13 Из последнего неравенства следует: практически достоверно, что значения нормально распределенной случайной величины X с параметрами и лежат в интервале µ ± 3. Иначе говоря, зная µ = Х и, можно указать интервал, в который с вероятностью Р = 99,73% попадают значения данной случайной величины. Такой способ оценки диапазона возможных значений X известен как «правило трех сигм» .
Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие события, исходя из принципа невозможности маловероятных событий, можно считать практически невозможными. В этом и состоит сущность правила трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения .
На практике правило трех сигм применяется так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то имеются основания предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально .
Пример 5.10 .
Известно, что для здорового человека рН крови является нормально распределенной величиной со средним значением (математическим ожиданием) 7,4 и стандартным отклонением 0,2 .
Определите диапазон значений этого параметра .
Для ответа на данный вопрос воспользуемся «правилом трех сигм»; с вероятностью, равной 99,73%, можно утверждать, что диапазон значений рН для здорового человека составляет [6,8; 8] .
Пример 5.11 .
Случайная величина X подчинена нормальному закону с математическим ожиданием µ = 375 и средним квадратическим отклонением = 25. Найти вероятность того, что значение этой случайной величины будет заключено в пределах от 300 до 425 .
Запишем вначале закон распределения. Общая формула имеет вид:
Нормально распределенные случайные величины широко встречаются в природе, на практике. Выдающимся русским математиком А.М. Ляпуновым была доказана центральная предельная теорема теории вероятностей, из которой вытекает следующее следствие: если случайная величина представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то эта случайная величина имеет распределение, близкое к нормальному .
Понятие о теореме Ляпунова В теории вероятностей некоторые весьма общие достаточные условия для сходимости распределения суммы независимых случайных величин к нормальному закону устанавливает теорема Ляпунова .
Приведем одну из простейших форм этой теоремы .
Теорема Ляпунова. Если X1, X 2. X i. X n – независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием µ и дисперсией 2, то при неограниченном n увеличении n закон распределения суммы X = X i неограниченно i =1 приближается к нормальному .
Сущность теоремы Ляпунова заключается в том, что сумма n независимых случайных величин, заданных произвольными распределениями, имеет распределение, которое по мере возрастания числа n стремится к нормальному при условии, что влияние каждой случайной величины невелико по сравнению с их суммарным влиянием. Значительное число случайных явлений, встречающихся в природе, протекает именно по такой схеме. В связи с этим теорема Ляпунова имеет большое значение, а нормальный закон является одним из основных в теории вероятностей .
Например, производится измерение некоторой физической величины с помощью измерительного прибора. Любое измерение дает лишь приблизительный результат, так как на него оказывают влияние очень многие случайные факторы (изменение температуры, колебания атомов, несовершенство органов зрения наблюдателя и др.). Каждый из этих факторов порождает ничтожную частную погрешность. Поскольку число факторов очень велико, совокупное их влияние дает уже заметную суммарную погрешность. Рассматривая суммарную погрешность как сумму очень большого числа взаимно независимых частных погрешностей, мы можем заключить, что суммарная погрешность будет иметь распределение вероятностей, близкое к нормальному. Опыт подтверждает справедливость такого заключения .
Вопросы для самоконтроля
1. Дайте определение случайной величины .
2. Какую случайную величину называют дискретной? непрерывной?
3. Что называют рядом распределения дискретной случайной величины? Как еще можно задать закон распределения дискретной случайной величины?
4. Что называют математическим ожиданием дискретной случайной величины?
5. Перечислите свойства математического ожидания случайной величины .
6. Что называют дисперсией случайной величины?
7. Перечислите свойства дисперсии случайной величины .
8. Что называют средним квадратичным отклонением случайной величины?
9. Какое распределение называют биномиальным?
10. Какое распределение называют распределением Пуассона?
11. Дайте определение функции распределения вероятностей. Перечислите свойства функции распределения .
12. Как, зная функцию распределения, найти вероятность попадания случайной величины в заданный интервал?
13. Какие свойства должна иметь некоторая функция для того, чтобы она могла быть функцией распределения?
14. Дайте определение плотности распределения вероятностей. Перечислите свойства плотности распределения. Существует ли плотность распределения у дискретной случайной величины?
15. Как, зная плотность распределения, найти вероятность попадания случайной величины в заданный интервал?
16. Чем различаются графики функций распределения дискретной и непрерывной случайных величин?
17. Что называют математическим ожиданием непрерывной случайной величины?
18. Что называют дисперсией непрерывной случайной величины?
19. Какое распределение называют равномерным?
20. Какое распределение называют нормальным?
а) Найдите вероятности р1 = P( X = 3) и р3 = P( X = 5), если известно, что р3 в 4 раза больше р1 .
б) Получив ответ на первый вопрос, постройте многоугольник распределения .
3. Случайная величина Х задана законом распределения
Найти математическое ожидание и среднее квадратическое отклонение ( X ). Построить многоугольник распределения .
4. Найти дисперсию случайной величины Х, зная закон ее распределения. Построить многоугольник распределения .
Чему равна вероятность P4 ( X = 0,8) ? Построить многоугольник распределения. Найти математическое ожидание и дисперсию .
6. Закон распределения случайной величины X задан следующей таблицей:
Вычислить ее математическое ожидание, дисперсию и среднее квадратическое отклонение .
7. Число -частиц, достигающих счетчика в некотором опыте за равные промежутки времени, является случайной величиной, распределенной по закону, заданному следующей таблицей:
того, что в результате опыта случайная величина X отклонится от своего математического ожидания не более чем на 1,5 .
18. Случайная величина X подчиняется нормальному закону распределения с математическим ожиданием 30 и дисперсией 10. Найти вероятность того, что значение случайной величины заключено в интервале (10;50) .
19. Среди 10 000 обследованных были выявлены два человека с редким заболеванием. Какова вероятность того, что из 10 000 случайно выбранных человек ровно у двух окажется редкое заболевание?
20. Известно, что для человека рН крови является случайной величиной, имеющей нормальное распределение с математическим ожиданием µ = 7,4 и средним квадратическим отклонением = 0,2. Найти вероятность того, что уровень рН находится между 7,35 и 7,45 .
21. Вероятность того, что среди стандартных ампул имеются ампулы с дефектом, равна 0,25. Составить биномиальное распределение вероятностей бездефектных взятых наугад 6 ампул .
22. Всхожесть семян лекарственного растения оценивается вероятностью 0,9. Составить биномиальное распределение вероятностей появления всхожих семян из пяти наугад взятых .
23. Вероятность изготовления нестандартного продукта равна 0,004. Найти вероятность того, что в партии из 1000 единиц окажется 5 нестандартных .
24. Из 1000 рецептов, поступивших в аптеку, 10 оказались неправильными. Какова вероятность того, что из 300 рецептов два будут неправильными?
25. Предполагается подвергнуть испытанию на прочность 100 таблеток. Для каждой таблетки вероятность разрушения равна 0,03. Какова вероятность того, что данная таблетка при испытании разрушится?
26. На аналитических весах производится взвешивание некоторого вещества без учета систематических ошибок. Случайные погрешности распределены по нормальному закону со средним квадратическим отклонением 2 мг. Вычислить вероятность того, что отклонение результата взвешивания от математического ожидания не превзойдет по абсолютной величине 1 мг .
27. По данным ОТК, брак при выпуске таблеток составляет 0,02 .
Найти вероятность того, что в серии из 1000 таблеток отклонение количества пригодных от 900 не превысит 0,05 .
28. Для определения средней урожайности лекарственного растения взято на выборку по 1м2 с каждого гектара. Известно, что дисперсия по всему участку не превышает 4 кг. Оценить вероятность того, что среднее значение урожайности от средней урожайности по всему участку отличается не более чем на 2 кг. Всего засеяно 5 га .
29. Вероятность спроса на данную лекарственную форму 0,8. Оценить вероятность того, что при 1000 обращениях в аптеку отклонение частоты спроса на данную лекарственную форму от вероятности спроса по абсолютной величине будет меньше 0,05 .
30. Дисперсия данных независимых случайных величин не превышает 4. Найти число величин, при котором вероятность отклонения их среднего арифметического от среднего арифметического их математических ожиданий не более чем на 0,25 превысит 0,99 .
§ 6.1. Генеральная и выборочная совокупности. Способы отбора Математическая статистика – раздел прикладной математики, непосредственно примыкающий к теории вероятностей. Основное отличие математической статистики от теории вероятностей состоит в том, что в математической статистике рассматриваются не действия над законами распределения и числовыми характеристиками случайных величин, а приближенные методы отыскания этих законов и характеристик по результатам экспериментов .
Разработка методов получения, описания и анализа экспериментальных данных, определенных в результате исследования случайных явлений, составляет предмет специальной науки – математической статистики. Эти данные принято называть статистическими. Статистические данные часто можно рассматривать как совокупность экспериментальных результатов, которые представляют собой набор возможных значений случайных однородных величин (роста, массы тела, содержания сахара в крови, длительности пребывания больного на койке и т. д.) .
Фундаментальными понятиями математической статистики являются генеральная совокупность и выборочная совокупность (выборка) .
Генеральная совокупность – это множество подлежащих статистическому изучению однородных объектов, которые характеризуются качественными или количественными признаками. Например: все жители Беларуси в фиксированный момент времени, или только все мужчины, или женщины, или дети; множество действительных чисел, лежащих между 0 и 1; количество больных ревматизмом на земном шаре и т.д. Число объектов генеральной совокупности называют ее объемом и обозначают N .
Чтобы изучить генеральную совокупность по какому-либо из её количественных признаков Х (острота зрения, показатели анализа крови и т.д.), нужно определить закон распределения данного признака и основные характеристики этого распределения (математическое ожидание, дисперсию). Однако на практике это сложно сделать (либо физически невозможно, либо экономически невыгодно). Поэтому исследуют только часть объектов, так называемую выборку .
Выборочная совокупность – множество объектов, случайно отобранных из интересующей нас генеральной совокупности для конкретного статистического исследования. Число объектов выборки называют ее объемом и обозначают n. Например, для контроля качества растворов в ампулах для инъекций на отсутствие в них механических загрязнений из серии 5000 ампул отбирают 150 ампул ( N = 5000 – объем генеральной совокупности, n = 150 – объем выборки) .
Исследование выборок дает приближенное оценочное значение для интересующего нас параметра. Следовательно, постоянная величина – значение нужной характеристики для генеральной совокупности – заменяется значением случайной величины, полученным по результатам выборки на основании некоторого правила. Главная цель выборочного метода – по вычисленной характеристике выборки как можно точнее определить соответствующую характеристику генеральной совокупности. Это возможно лишь в том случае, когда отобранная для работы часть объектов репрезентативна целому, т.е. типична, обладает теми же основными чертами, что и все целое. Иначе говоря, выборка должна быть представительной, т.е. по возможности полнее «представлять» свою генеральную совокупность. Это одно из важнейших требований, предъявляемых к выборке, невыполнение которого ведет к грубым ошибкам и обесценивает результаты исследования. Например, если при изучении заболеваемости населения республики (генеральная совокупность) ишемической болезнью сердца в качестве выборки будет взята группа студентов, то результаты окажутся ошибочными, поскольку свойства выборки не будут соответствовать свойствам генеральной совокупности, как и в случае, когда в качестве выборки будут взяты только пациенты кардиологического диспансера. Репрезентативность выборки обеспечивается ее достаточным объемом и определенными правилами ее формирования .
В зависимости от техники отбора объектов из генеральной совокупности выборки делятся на повторные и бесповторные .
Если выборку отбирают по одному объекту, который обследуют и снова возвращают в генеральную совокупность, то выборка называется повторной. Если объекты выборки не возвращаются в генеральную совокупность, то выборка называется бесповторной. На практике обычно пользуются бесповторной выборкой .
На практике применяются различные способы отбора. Различают случайный отбор, т. е. проводимый с помощью какого-либо случайного механизма, и неслучайный (по закономерности). В статистике применяется в основном случайный отбор как более надежный в отражении свойств генеральной совокупности .
Простым случайным отбором называется отбор, удовлетворяющий следующим требованиям:
1. Выбор является случайным;
2. Каждый элемент совокупности может быть выбран;
3. Каждый элемент выбирается независимо от остальных;
4. Все элементы выборки получаются в равных условиях .
Осуществить простой отбор можно различными способами. Например, для извлечения n объектов из генеральной совокупности объема N поступают так: выписывают номера от 1 до N на карточках, которые тщательно перемешивают и наугад вынимают одну карточку, объект, имеющий одинаковый номер с извлеченной карточкой, подвергают обследованию; затем карточка возвращается в пачку и процесс повторяется, т. е. карточки перемешиваются, наугад вынимают одну из них и т. д. Так поступают n раз; в итоге получают простую случайную повторную выборку объема n .
Если извлеченные карточки не возвращать в пачку, то выборка будет простой случайной бесповторной .
Так можно выбирать группу людей для обследования, ампулы партии для испытания, лекарственные препараты для контроля и т. д .
В реальных условиях простой случайный отбор не всегда осуществим. Он является как бы эталонным идеальным отбором. Его нельзя, например, осуществить из бесконечной генеральной совокупности (время обслуживания, отклонение результата измерения от нормы), из генеральной совокупности, образование которой не завершено и может продолжаться бесконечно долго .
Виды реальных отборов:
1. Типическим называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типической» части. Например, если ампулы изготовляют на нескольких станках, то отбор производят не из всей совокупности ампул, произведенных всеми станками, а из продукции каждого станка в отдельности. Типическим отбором пользуются тогда, когда обследуемый признак заметно колеблется в различных типических частях генеральной совокупности .
2. Механическим называют отбор, при котором элементы генеральной совокупности выбираются по какой-либо закономерности. Например, измерения производятся через равные промежутки времени;
контролируется каждая десятая ампула, сходящая с конвейера; каждый пятый человек по списку и т.д .
3. Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергаются сплошному обследованию. Например, контролю подвергается не одна таблетка лекарства, а упаковка, не один человек из какой-либо группы, а вся группа. Серийным отбором пользуются тогда, когда обследуемый признак колеблется в различных сериях незначительно .
4. Субъективным называют отбор на основе какого-либо субъективного принципа. Например, обследуются не вся партия лекарственных препаратов, а лишь одна, наиболее подозрительная часть. Он экономит время, средства, но может привести к большим ошибкам .
5. Выбор с помощью случайных независимых измерений (температура среды, загрязненность атмосферы). Характерен для естественнонаучных исследований .
На практике часто применяется комбинированный отбор, при котором сочетаются указанные выше способы .
§ 6.2. Статистическое распределение выборки .
Дискретный и интервальный ряды распределения Итак, мы хотим знать распределение признака X в генеральной совокупности, но реально исследуем лишь некоторую выборку из неё .
В серии экспериментов, проводимых с выборкой, величина X принимает определенные значения. Эти значения, записанные для всех элементов выборки в том порядке, в котором они были получены в опытах, представляют собой простой статистический ряд. Полученные данные и подлежат статистической обработке, статистическому анализу .
Первый шаг при обработке этого материала – наведение в нем определенного порядка, ведущего к получению статистического распределения выборки .
Статистическое распределение выборки – это составление дискретного или интервального рядов соответственно, когда количественный признак, по которому исследуют данную выборку, является дискретной или непрерывной величиной .
Дискретный ряд распределения
Пусть из генеральной совокупности извлечена выборка объемом n. В имеющемся у нас простом статистическом ряду варианта x1 встречается (повторяется) m1 раз, x2 – m2 раза. xk – mk раз и т.д. Наблюдавшиеся значения xi признака X называют вариантами, а последовательность вариант, записанную в возрастающем порядке, вариационным рядом .
Дискретный вариационный ряд удобно представить в виде таблицы, включающей в себя:
1) различные по значению варианты xi, расположенные в определенной, заранее выбранной последовательности (обычно в порядке возрастания);
2) mi – частоты вариантов, т.е. числа наблюдений (повторений) варианты xi в простом статистическом ряду;
– относительные частоты вариант, т.е. отношения часpi* = n тот mi к объему выборки n ; они являются выборочными (эмпирическими) оценками вероятностей появления значений xi .
Каждая относительная частота указывает, какая доля общего объма выборки приходится на данное значение вариантов xi .
Итак, для дискретной величины X вариационный ряд – статистическое распределение выборки – имеет следующий вид:
Напомним, что под распределением дискретной случайной величины в теории вероятностей понимается соответствие между возможными значениями случайной величины и их вероятностями; в математической статистике – соответствие между наблюдаемыми вариантами xi и их частотами или относительными частотами .
Пример 6.1 .
В результате отдельных испытаний активности тетрациклина были получены следующие значения (в единицах действия на 1 мг): 925, 940, 760, 905, 995, 965, 940, 925, 940, 905. Составить ряд распределения .
Расположив значения активности, частоты и относительные частоты в порядке возрастания, получим дискретный ряд распределения в виде таблицы:
Полезность подобного представления данных очевидна по следующей причине: мы получаем практически важный результат – возможность оценить более и менее вероятные значения признака .
Пример 6.2 .
Анализируемый показатель X – масса тела новорожденного. Определение массы тела 100 новорожденных показало, что минимальная масса составляет 2,7 кг, максимальная – 4,4 кг. Составить ряд распределения .
Интервал (2,7 4,4) кг разбиваем на 10 равных интервалов 4,4 2,7 (k = 100 = 10) шириной x = = 0,17 кг и строим интервальный ряд:
Для непрерывной случайной величины обычно строят гистограммы частот или гистограммы относительных частот .
Гистограммой частот называют диаграмму, состоящую из вертикальных прямоугольников, основаниями которых являются интервалы m длиной x, а высоты равны отношению i (плотности частоты) .
x Для построения гистограммы частот на оси абсцисс откладывают интервалы значений исследуемого показателя (интервалы вариант) и на m них строят прямоугольники высотой i. Площадь i-го прямоугольника x m равна x i = mi, т.е. равна количеству вариант в i-м интервале. Слеx довательно, площадь гистограммы частот равна сумме частот для всех интервалов, иначе говоря, равна объему выборки .
Гистограмма относительных частот отличается от предыдущей гистограммы тем, что на ней высоты прямоугольников равны отношеm нию i, т. е. равны плотности относительной частоты (эмпирической nx плотности вероятности). В этом случае площадь i-го прямоугольника mi равна x = pi* – относительной частоте вариант, попавших в i-й nx интервал (рис.6.2). Напомним, что p* – оценка вероятности попадания значений X в выбранный интервал. Площадь гистограммы относительных частот равна сумме относительных частот для всех интервалов, т. е. равна единице .
Отметим, что гистограммой называют и фигуру, состоящую из вертикальных прямоугольников, высотами которых являются непосредственно частоты mi для соответствующих интервалов или относительные частоты (в нормированной гистограмме), а также относительные частоты в процентах (процентная гистограмма). Два последние варианта позволяют сравнивать гистограммы, построенные на одних и тех же интервалах, но для различных выборок из той же генеральной совокупности .
Рис. 6.2
Важно, что гистограммы можно использовать для оценки закона распределения признака в генеральной совокупности. Соединяя средние точки верхних оснований прямоугольников гистограммы относительных частот плавной линией, можно по данным выборки получить примерный вид графика зависимости плотности вероятности f (x). Можно предположить, что анализируемый показатель в генеральной совокупности распределен по нормальному закону, т. е. нормальный закон является вероятностной моделью для данного признака .
Пример 6.3 .
Построить полигон частот и относительных частот по распределению выборки
Предположим, что изучается некоторая случайная величина X, закон распределения которой неизвестен. Требуется определить этот закон на основании опыта или проверить экспериментально гипотезу о том, что величина X подчинена тому или иному закону. С этой целью над случайной величиной X проводится ряд независимых опытов и составляется статистическое распределение выборки количественного признака X. Чтобы получить представление о распределении случайной величины X, строят эмпирическую функцию распределения .
Эмпирической функцией распределения (функцией распределения выборки) – называют функцию F * ( x), определяющую для каждого значения x относительную частоту события X x :
m( x ) F * ( x) =, n где m(x) – число наблюдений, при которых значение признака X меньше х; n – объём выборки .
В отличии от эмпирической функции распределения F * ( x) выборки, функцию распределения F (x) генеральной совокупности называют теоретической функцией .
Различие между эмпирической F * ( x) и теоретической F (x) функциями состоит в том, что F (x) определяет вероятность события X x, а F * ( x) – относительную частоту этого же события. Поэтому эмпирическую функцию распределения выборки F * ( x) можно использовать для приближённого представления теоретической функции распределения генеральной совокупности .
Функция F * ( x) имеет следующие свойства:
1. Значения эмпирической функции принадлежит отрезку [0;1] .
2. F * ( x) – неубывающая функция .
3. Если х1 – наименьшая варианта, то F * ( x) = 0 при x x1 ; если xk – наибольшая варианта, то F * ( x) = 1, при x xk .
График эмпирической функции представлен на рисунке 6.5:
§ 6.5. Понятие о несмещенности, состоятельности и эффективности оценок параметров распределения К статистическому распределению выборки применимы многие характеристики распределения вероятностей. Таковы например, выборочная средняя, выборочная дисперсия, выборочное среднее квадратическое отклонение .
Характеристики статистического распределения выборки применяются для оценки неизвестных параметров теоретического распределения вероятностей. Различают точечные и интервальные оценки .
Точечной называют оценку, которая определяется одним числом .
Пусть мы имеем выборку, состоящую из значений х1, х2. хn, взятую из генеральной совокупности с известным законом распределения, параметр имеет постоянное, но неизвестное значение. При условии, что оценке подлежит единственный параметр, точечная оценка представляет собой функцию от результатов наблюдений * ( х1, х2. хn ).Для того, чтобы оценка давала хорошее приближение, она должна удовлетворять определённым требованиям: быть несмещённой, эффективной и состоятельной .
Точечная оценка * параметра называется несмещенной, если её математическое ожидание равно оцениваемому параметру при любом объёме выборки, т.е. M (* ) = .
Оценку, математическое ожидание которой не равно оцениваемому параметру, называют смещенной .
За меру точности несмещенной оценки * для параметра принимают дисперсию D(* ). Оценку с наименьшей дисперсией называют наилучшей .
В качестве характеристики для сравнения точности различных оценок применяют эффективность – отношение дисперсий наилучшей оценки и данной несмещенной оценки .
При большом количестве наблюдений обычно требуется, чтобы выбранная оценка * стремилась по вероятности к истинному значению неизвестного параметра, т.е.
чтобы для любого 0 выполнялось равенство:
( ) lim P * = 1 n Такие оценки называют состоятельными .
Из отмеченных требований, предъявляемых к оценке, наиболее важными являются требования несмещенности и состоятельности .
§ 6.6. Оценки параметром генеральной совокупности по ее выборке
Выборочная мода Moв – варианта, которая чаще всего встречается в исследуемой выборке, т. е. имеет наибольшую частоту .
Для того, чтобы охарактеризовать рассеяние значений количественного признака Х генеральной совокупности вокруг своего среднего значения, вводят следующую характеристику – генеральную дисперсию .
§ 6.7. Доверительный интервал для оценки математического ожидания нормального распределения. Распределение Стьюдента Под интервальной оценкой параметров генеральной совокупности понимают определение некоторого интервала, в который с заданной вероятностью попадает истинное значение исследуемого признака .
Такой интервал называется доверительным интервалом, а вероятность того, что истинное значение оцениваемой величины находится внутри этого интервала, – доверительной вероятностью или надежностью .
В медицинской литературе для этой величины используется термин «вероятность безошибочного прогноза». Обозначим ее. Значения задаются заранее (обычно в медико-биологических исследованиях выбирают значения = 0,95 = 95% или = 0,99 = 99%), после чего находят соответствующий доверительный интервал. 1 Для построения надежных интервальных оценок необходимо знать закон, по которому оцениваемый случайный признак распределен в генеральной совокупности .
Рассмотрим, вначале для малых выборок ( n 30 ), как строится интервальная оценка генеральной средней x г = М ( Х ) признака, который в генеральной совокупности распределен по нормальному закону.
В этом случае интервальной оценкой (с доверительной вероятностью ) генеральной средней (математического ожидания) x г = М ( Х ) количественного признака X по выборочной средней x в при неизвестном г является доверительный интервал:
xв М ( Х ) xв +, или в другой форме записи:
x г = М ( Х ) = xв ±, Иногда вместо доверительной вероятности используется величина = 1 -, кото
Пусть случайная величина X генеральной совокупности распределена нормально, причем среднее квадратическое отклонение неизвестно. Требуется оценить неизвестное математическое ожидание при помощи доверительных интервалов .
По данным выборки из независимых наблюдений можно получить случайную величину ( x M ( X )) T=, Sx которая имеет распределение Стьюдента с f = n 1 степенями свободы;
здесь x – выборочная средняя, S x – оценка среднего квадратического отклонения выборочной средней, M ( X ) – математическое ожидание .
Плотность вероятности величины Т (ее возможные значения обозначены через t) выражается формулой f + 1 (t ) = f +1 f ( f / 2)!(1 + t / f ) Мы видим, что распределение Стьюдента определяется параметром n – объемом выборки (или, что то же, числом степеней свободы f = n 1 ) и не зависит от неизвестных параметров M ( X ) и ; эта особенность является его большим достоинством) .
Кривая плотности вероятности приведена на рисунке 6.7. Как видно из рисунка, кривая распределения симметрична относительно оси, проходящей через t = 0 ; ее ветви асимптотически приближаются к оси Оt. С ростом числа степеней свободы распределение Стьюдента приближается к нормальному и уже при n 30 практически не отличается от него .
1. В чём состоит основное отличие математической статистики от теории вероятностей?
2. Что понимается под статистическими данными?
3. Дайте определение генеральной совокупности. Что понимается под объёмом генеральной совокупности? Приведите примеры .
4. Дайте определение выборочной совокупности. Что понимается под объёмом выборочной совокупности? Приведите примеры .
5. В чём состоит главная цель выборочного метода?
6. Дайте определение повторной, бесповторной выборки .
7. Каким требованиям должен удовлетворять простой случайный отбор?
8. Перечислите виды реальных отборов. Дайте определение каждому виду реальных отборов .
9. Что такое простой статистический ряд?
10. Что понимается под статистическим распределением выборки?
11. Что понимается под вариационным рядом распределения?
12. Укажите все составные части таблицы, с помощью которой может быть представлен дискретный вариационный ряд? интервальный ряд?
13. Дайте определение полигону частот, полигону относительных частот .
14. Что понимают под гистограммой частот, гистограммой относительных частот?
15. Что такое эмпирическая функция распределения? Для каких целей необходимо ее построение?
16. Назовите основные свойства эмпирической функции распределения .
Дайте необходимые пояснения для каждого из ее свойств .
17. Что понимается под точечной оценкой?
18. При каких условиях точечная оценка является несмещенной? смещенной?
19. Что такое эффективность?
20. Какие оценки называются состоятельными?
21. Что такое выборочное среднее? Запишите соответствующую формулу .
22. Дайте определение выборочной дисперсии. Запишите соответствующую формулу .
23. Что такое среднее квадратическое отклонение? Запишите соответствующую формулу .
24. Что такое размах выборки?
25. Что понимают под интервальной оценкой параметров генеральной совокупности?
26. Дайте определение доверительному интервалу .
27. Что называется доверительной вероятностью или надёжностью?
28. Сформулируйте принцип построения интервальной оценки генеральной средней х г = М ( Х ) признака, который в генеральной совокупности распределен по нормальному закону для выборок объёма n 30 ( n 30 ). Запишите соответствующие формулы .
29. Чем определяется и от чего зависит (не зависит) распределение Стьюдента?
30. Что является интервальной оценкой математического ожидания в соответствии с распределением Стьюдента? Запишите формулу .
Задания для решения
1. Записать выборку 5, 6, 7, 10, 7, 2, 7, 7, 4, 2, 4 в виде: а) вариационного статистического ряда, б) интервального статистического ряда .
2. Представить в виде статистического дискретного ряда данные о длине листьев садовой земляники (в см) и построить полигон частот:
8,2; 9,7; 6,6; 7,4;6,4; 6,6; 6,8; 8,4; 7,1; 8,0; 9,0; 6,0; 7,6; 8,1; 11,8; 5,8; 9,3;
7,3; 8,2; 7,2; 7,2; 6,4; 7,7; 9,0; 8,1; 7,1; 7,1; 8,8; 7,5; 9,2; 7,5; 6,8; 7,0; 6,4;
7,4; 8,2; 6,3; 7,0; 8,1; 7,0; 7,1; 8,7; 6,3; 8,6; 7,7; 7,3; 8,0; 8,4; 9,3 .
3. В приведенной ниже таблице указаны значения случайной величины и число случаев, в которых они наблюдалось (m). Построить полигон частот .
9. Построить гистограмму изменения кровяного давления у 200 практически здоровых женщин в возрасте 60—65 лет по данным статистического распределения:
12. Ниже приведены результаты измерения веса (мг) случайно отобранных 32 препаратов: 2,00; 4,25; 5,00; 4,25; 5,15; 2,25; 5,30; 4,25;
2,75; 3,10; 4,40; 5,30; 4,50; 5,45; 3,25; 3,40; 3,65; 4,50; 4,75; 5,80; 5,75; 3,8;
4,85; 5,95; 6,45; 4,00; 4,90; 4,90; 4,15; 7,00; 7,45; 8,00. Построить гистограмму относительных частот распределения веса препарата, сгруппировав данные в 5 интервалов .
13. Наблюдения за сахаром крови у 50 человек дали такие результаты: 3,94; 3,84, 3,86; 4,06; 3,67; 3,97; 3,76; 3,61; 3,96; 4,04; 3,82; 3,94;
3,98; 3,57; 3,87; 4,07; 3,99; 3,69; 3,76; 3,71; 3,81; 3,71; 4,16; 3,76; 4,00;
3,46; 4,08; 3,88; 4,01; 3,93; 3,92; 3,89; 4,02; 4,17; 3,72; 4,09; 3,78; 4,02;
3,73; 3,52; 3,91; 3,62; 4,18; 4,26; 4,03; 4,14; 3,72; 4,33; 3,82; 4,03 .
Построить по этим данным интервальный вариационный ряд с равными интервалами и изобразить его графически, начертить гистограмму .
14. Для выборки 2, 4, 6, 8, 10 определить: выборочное среднее, выборочную дисперсию, среднее квадратическое отклонение .
15. При измерениях получены следующие значения некоторых величин:
а) 19, 20, 21; б) 37, 38, 37, 39, 40; в) 3, 2, 3; г) 4, 5, 6, 4 .
Дать интервальную оценку истинного значения измеряемой величины, рассматривая полученные значения как малую выборку. Доверительную вероятность принять равной 0,95 и 0,99 .
16. Произведено 5 независимых измерений толщины пластины .
Получены следующие результаты: 2,15; 2,18; 2,14; 2,16; 2,17. Оценить истинное значение толщины пластины с помощью доверительного интервала, принимая доверительную вероятность 0,95 .
17. При подсчете количества листьев у одного из лекарственных растений были получены следующие данные: 8, 10, 7, 9, 11, 6, 9, 8, 7 .
Вычислить выборочную среднюю и оценку среднего квадратического отклонения выборочной средней .
18. При измерении некоторой величины Х получены следующие результаты: 10,9; 10,7; 11,0; 10,5; 10,6; 10,4; 11,3; 10,8; 11,2; 10,9; 10,8;
10,3; 10,5; 10,9; 10,9; 10,6; 11,3; 10,8; 10,9; 10,7. Вычислить точечную и интервальную оценки для величины X с доверительной вероятностью 0,95 .
19. Исследуя продолжительность (в секундах) физической нагрузки до развития приступа стенокардии у 12 человек с ишемической болезнью сердца, получили следующие данные: 289; 203; 359; 243; 232;
210; 215; 246; 224; 239; 220; 211. Найдите среднюю, среднее квадратическое отклонение. Можно ли считать, что данная выборка извлечена из совокупности с нормальным распределением?
20. При исследовании клинической оценки тяжести серповидноклеточной анемии была получена выборка объёма 30:
0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 5, 5, 5, 5, 6, 7, 9, 10 .
Найдите среднюю, среднее квадратическое отклонение. Можно ли считать, что выборка извлечена из совокупности с нормальным распределением?
21. Случайной величиной является скорость распространения механической волны v (м/с), измеренная на пораженных участках кожи у больных псориазом в различных стадиях. Получен простой статистический ряд для разных стадий .
Регрессирующая стадия: 38, 39, 41, 41, 38, 43, 40, 40, 42, 38, 38, 39, 41, 42, 41, 42, 41, 39, 43, 38, 42, 43, 40, 39, 40, 38, 43, 42, 39, 42 .
Стационарная стадия: 49, 46, 54, 49, 50, 50, 46, 56, 49, 46, 54, 50, 56, 49, 46, 53, 52, 52, 51, 51, 53, 53, 50, 47, 47, 55, 55, 50, 54, 56 .
Прогрессирующая стадия: 65, 58, 58, 62, 64, 65, 64, 68, 68, 67, 59, 66, 66, 68, 70, 72, 69, 67, 65, 68, 71, 71, 70, 67, 72, 69, 68, 68, 62, 60 .
Построить и сравнить гистограммы. Найти и сравнить числовые характеристики статистических рядов .
22. При измерении скорости распространения механических волн в коже щеки после процедуры криомассажа у пациенток с разным типом кожи получены значения v (м/с), представленные простым статистическим рядом .
Сухая кожа: 38, 58, 46, 39, 49, 62, 62, 49, 43, 44, 68, 41, 54, 64, 64 .
Жирная кожа: 41, 54, 54, 41, 64, 42, 56, 56, 42, 56, 56, 65, 65, 39 .
Построить и сравнить гистограммы. Найти и сравнить числовые характеристики рядов .
23. Случайной величиной является значение скорости v (м/с) распространения механической волны в рубцово-измененных тканях разного типа. Получен простой статистический ряд для разных рубцов .
Неосложненный рубец: 40, 39, 42, 42, 43, 40, 41, 45, 42, 40, 44, 39, 40, 40, 41, 41, 43, 42, 45, 42, 39, 38, 40, 45, 43, 42, 39, 38, 41, 42 .
Гипертрофический рубец: 60, 64, 65, 63, 66, 59, 58, 67, 71, 72, 72, 68, 67, 70, 69, 69, 68, 67, 70, 67, 66, 67, 70, 69, 71, 67, 70 .
Келлоидный рубец: 80, 85, 88, 89, 90, 95, 98, 99, 95, 100, 92, 96, 97, 99, 98, 89, 89, 100, 102, 105, 99, 98, 82, 84, 83, 101, 99, 98, 97, 100 .
Построить и сравнить гистограммы для трех типов рубцов. Найти и сравнить числовые характеристики рядов .
24. На аналитических весах производится взвешивание некоторого вещества без учета систематических ошибок. Случайные погрешности распределены по нормальному закону со средним квадратическим отклонением 2 мг. Найти вероятность того, что отклонение результата взвешивания от математического ожидания не превзойдет по абсолютной величине 1 мг .
25. При исследовании частоты дыхания при выборке объёмом 15 человек были получены выборочная средняя 18,5 и среднее квадратическое отклонение 0,6. Дать интервальную оценку математического ожидания с доверительной вероятностью 0,95 .
Теория ошибок – изучение и оценка погрешностей в измерениях .
Опыт показывает, что ни одно измерение, как бы тщательно оно ни проводилось, не может быть совершенно свободно от ошибок. Поскольку в основе любой науки и ее применений лежат измерения, исключительно важно уметь рассчитывать эти ошибки и сводить их к минимуму .
Целью любого измерения некоторой физической величины является получение ее истинного значения. Однако это весьма непростая задача из-за различных ошибок (погрешностей), неизбежно возникающих при измерениях .
Все измерения делятся на прямые и косвенные. Прямые измерения производятся с помощью приборов, которые непосредственно измеряют исследуемую величину. При косвенных измерениях определяемую величину вычисляют по некоторой формуле, а параметры, входящие в эту формулу, находят путем прямых измерений. Погрешность, возникающая при прямых измерениях, естественно, ведет к появлению ошибки косвенно определяемой величины .
Все ошибки разделяют на систематические, случайные и грубые (промахи) .
Систематические ошибки зависят от неправильных показаний измерительных приборов, неправильно градуированных приборов, мерных колб, пипеток, бюреток, невыверенных разновесов и др. Систематические ошибки должны быть устранены. Для этого перед работой все приборы необходимо прокалибровать, неисправные заменить на исправные и т. д. В показания выверенных приборов следует внести соответствующие поправки .
Случайные ошибки возникают от различных помех, несовершенства органов чувств экспериментатора и других случайных причин. Ограниченная точность приборов, изменение условий, при которых проводится опыт (особенно это имеет значение при параллельных определениях), также приводят к возникновению случайных ошибок .
Грубые ошибки в основном связаны с субъективными свойствами экспериментатора: невнимательностью и неряшливостью, занятием посторонними делами во время работы и др. Это приводит к неверным отсчетам, неправильным записям. При обработке результатов анализа грубые ошибки во внимание не принимают – их отбрасывают .
Необходимо отметить, что ошибки измерений, как правило, подчиняются нормальному закону распределения .
§ 7.2. Абсолютная и относительная погрешности, класс точности Во всякой экспериментальной работе большое значение имеет точность измерений, воспроизводимость и правильность результатов анализа. Опыт показывает, что любая измеряемая величина имеет свою ошибку; это обусловлено несовершенством приборов, их ограниченной точностью, влиянием внешних условий, загрязнениями, неправильно проведенными записями и пр .
Кроме того, при измерениях могут появляться ошибки, зависящие от ряда причин, природа которых остается неизвестной. Поэтому в результате эксперимента аналитик всегда устанавливает только приближенное значение определяемой величины, но никогда не может получить истинного ее значения. Вследствие этого измеряемая величина имеет некоторую ошибку, величину которой принято определять как абсолютную и относительную ошибки (погрешности) .
Абсолютной погрешностью x измеряемой величины называют разницу между полученным результатом измерения хизм и истинным (или более достоверным) значением хист определяемой величины:
Абсолютную погрешность определяют в абсолютных единицах, ее размерность отвечает размерности измеряемой величины .
Относительной погрешностью измеряемой величины называют отношение абсолютной погрешности x к точному значению хист определяемой величины:
хист Относительная погрешность является отношением двух величин одной и той же размерности, поэтому относительные погрешности – всегда безразмерные величины. Их, как правило, выражают в процентах .
Точностью измерительного прибора называется та наименьшая величина, которую можно вполне надежно определить с его помощью .
Точность указывается либо на самом приборе, либо в прилагаемом к нему паспорте. Если точность прибора неизвестна и измерения проводятся путем сравнения измеряемой величины с какой-либо шкалой, то точность прибора определяется половиной цены наименьшего деления шкалы прибора (например, при измерении длины линейкой или температуры термометром). Если измерения проводятся прибором, снабженным нониусом (например, штангенциркулем), точность прибора принимается равной разности между ценой деления прибора и ценой деления нониуса, т. е. точностью нониуса (так, точность штангенциркуля равна 0,1 мм) .
При измерении с помощью прибора полученный результат отличается от истинного значения измеряемой величины и может быть больше или меньше его. Поэтому величину погрешности измерения записывают со знаками плюс и минус. Например, термометр с ценой деления 0,1°C показывает температуру 36,6°C. Абсолютная погрешность измерения t = ±0,05°C, следовательно, измеряемая температура равна одному из чисел между 36,55°C и 36,65°C. Результат измерения записывается в виде t = (36,6 ± 0,05)°C .
Пусть значение z = f ( x, y ) может быть рассчитано по измеренным с помощью приборов значениям величин х и у, абсолютные погрешности которых x и y. Абсолютная погрешность величины z рассчитывается по формуле z = dz = f x ( x, y ) dx + f y ( x, y ) dy где dx = x, dy = y всегда положительны .
z Относительная погрешность величины z определяется как и z обычно выражается в процентах .
Классом точности или приведенной относительной погрешностью электроизмерительного прибора называют выраженное в процентах отношение максимальной абсолютной погрешности x к наибольшему значению измеряемой величины xmax (предел измерения), которое можно определить данным прибором:
x 100 k xmax, откуда x = k= .
xmax 100 Отношение абсолютной погрешности к значению измеряемой величины определяет относительную погрешность, которая и используется в качестве характеристики точности прибора. Если относительная погрешность определена в долях (процентах) диапазона измерения, то ее называют приведенной погрешностью. По ее величине и судят о классе точности прибора.
Относительная погрешность зависит от величины отсчета по прибору:
x k xmax x = 100 = .
x x § 7.3. Прямые (непосредственные) измерения .
Оценка случайных погрешностей прямых измерений
1. Что изучает теория ошибок?
2. В чем заключается цель любого измерения некоторой физической величины?
3. Дайте определение прямому измерению, косвенному измерению .
4. Перечислите виды ошибок. Дайте соответствующие определения и приведите примеры .
5. Что называется абсолютной погрешностью измерения? Запишите формулу .
6. Что называется относительной погрешностью измерения? Запишите формулу .
7. Что называется точностью измерительного прибора?
8. Дайте определение классу точности. Запишите формулу .
9. Что такое приведенная погрешность? Запишите формулу .
10. Перечислите и дайте определения каждому этапу оценки случайных погрешностей прямых измерений .
11. Что такое коэффициент Стьюдента? Правила нахождения данного коэффициента .
12. Перечислите и дайте определения каждому этапу оценки случайных погрешностей косвенных измерений .
Задания для решения
1. При подсчете количества листьев у одного из лекарственных растений были получены следующие данные: 8, 10, 7, 9, 11, 6, 9, 8, 10,
7. Вычислить выборочную среднюю и оценку среднего квадратического отклонения выборочной средней .
2. В результате десяти измерений диаметра капилляра в стенке легочных альвеол были получены следующие данные: 2,83 мкм; 2,82;
2,81; 2,85; 2,87; 2,86; 2,83; 2,85; 2,83; 2,84 мкм. Вычислить оценку истинной величины диаметра капилляра и абсолютную и относительную погрешности при доверительной вероятности 0,95 .
3. В результате десяти одинаковых проб были получены следующие значения содержания марганца: 0,69%; 0,70; 0,67; 0,66; 0,67; 0,68;
0,67; 0,69; 0,68; 0,68%. Вычислить оценку истинного содержания марганца и абсолютную и относительную погрешности при доверительной вероятности 0,95 .
4. При определении микроаналитическим способом содержания азота в данной пробе были получены следующие результаты: 9,29%;
9,38; 9,35; 9,43; 9,53; 9,48; 9,61; 9,68%. Оценить истинное содержание в пробе и абсолютную и относительную погрешности при доверительной вероятности 0,95 .
5. При фотоэлектроколориметрическом определении концентрации ацетилсалициловой кислоты на основании реакции с сульфатом меди и пиридином были получены следующие результаты: 99,2%; 99,0;
98,9; 99,3; 98,8; 99,1 %. Вычислить среднее значение полученных результатов и абсолютную и относительную погрешности при доверительной вероятности 0,95 .
6. С помощью колориметра-нефелометра проведено измерение концентрации Сх неизвестного окрашенного раствора путем сравнения с раствором известной концентрации С0. Расчетная формула для определения концентрации вещества имеет вид:
d С x = C0 0, dx где d0 и dx – толщины слоев, одинаково поглощающих монохроматический свет, C0 = 2% (принять за точное число).
В пяти опытах получены следующие результаты:
Оценить истинное значение измеряемой концентрации с доверительной вероятностью = 0,95. Оценить абсолютную и относительную погрешность измерения .
7. С помощью моста Уитстона проведено измерение неизвестного сопротивления. Расчетная формула имеет вид:
Оценить истинное значение сопротивления с доверительной вероятностью = 0,95. Оценить абсолютную и относительную погрешность измерения .
8. Мощность тока Р определена по силе тока I и напряжению U, которые измерялись непосредственно и были получены следующие результаты:
Расчетная формула имеет вид:
P = IU Оценить истинное значение мощности тока с доверительной вероятностью = 0,95. Оценить абсолютную и относительную погрешность измерения .
9. Объем цилиндра V = ( / 4)hd 2, где h – высота, d – диаметр цилиндра. В пяти опытах получены следующие результаты:
Оценить истинное значение объема цилиндра с доверительной вероятностью = 0,95. Оценить абсолютную и относительную погрешность измерения .
10. Изготовлены таблетки цилиндрической формы. Взвешены 5 таблеток и измерены толщина h и диаметр d каждой. Результаты измерений занесены в таблицу:
При решении прикладных задач, имеющих вероятностную постановку, зачастую необходимо установить неизвестный закон распределения генеральной совокупности, в других случаях при известном законе распределения требуется уточнить параметры распределения, равенство их определенному числу и сравнить либо параметры по различным выборкам, либо сами выборки .
В подобных случаях выдвигаются определенные гипотезы, например «закон распределения генеральной совокупности, является биномиальным» или «среднее генеральной совокупности, распределенной по нормальному закону, равно нулю» и т.д. Возможны и другие гипотезы относительно параметров и выборок .
Статистической гипотезой называют предположение о неизвестном законе распределения генеральной совокупности либо о параметрах известных распределений. Статистическая гипотеза проверяется, исходя из выборочных данных, статистическими методами. К статистической проверке гипотез сводятся задачи сравнительной проверки и оценки различных процессов: эффективности лечения, продолжительности болезни и восстановительного периода, тяжести заболевания, сравнения лечебно-диагностических методик, различных характеристик процесса, препаратов и медицинской техники, экономичности, мер профилактики и т.д .
Утверждения типа «В 2023 г. Земля может сойти со своей орбиты»
(Нострадамус), «Тысячу лет назад нашу планету посещали инопланетяне» являются гипотезами, но не статистическими, так как эти события являются уникальными (не массовыми) .
Статистические гипотезы, не использующие допущений о конкретном законе распределения, называют непараметрическими гипотезами, в противном случае гипотезы называют параметрическими. Непараметрические гипотезы – понятие более общее, нежели параметрические, так как методика их проверки не требует знания закона распределения, что, несомненно, является их достоинством. Однако методы проверки параметрических гипотез более эффективны, так как используют большее количество информации о случайных величинах (закон распределения известен) .
Статистические гипотезы бывают простыми и сложными. Простой называют гипотезу, которая полностью однозначно определяет функцию распределения (т.е. закон распределения) случайной величины. Гипотезу называют сложной, если она состоит из объединения конечного или бесконечного числа простых гипотез .
Основную гипотезу, которую намереваются проверять, называют нулевой гипотезой и обычно обозначают H 0 .
Для каждой нулевой гипотезы обязательно существует альтернативная гипотеза, противоречащая нулевой. Такую альтернативную гипотезу называют конкурирующей гипотезой. Обозначим ее H1 .
Нулевая и конкурирующая гипотезы всегда несовместны, но не обязательно образуют полную систему событий .
Выдвинутые гипотезы H 0 и H1 проверяются на истинность на основе выборочных наблюдаемых данных статистическими методами, т.е., обладая лишь информацией по выборке (неполной информацией), о генеральной совокупности можно судить не однозначно, а с определенной вероятностью. При этом, полагая нулевую гипотезу справедливой (потому она и считается основной, что из каких-то соображений мы верим в ее истинность), мы заинтересованы в том, чтобы признать нулевую гипотезу верной, а конкурирующую гипотезу отвергнуть. Но вполне возможно, что справедлива не нулевая, а конкурирующая гипотеза, в этом случае наш интерес, наоборот, в наибольшей вероятности принятия гипотезы H1 и, следовательно, в отвержении нулевой гипотезы H 0 .
Например, пусть партию лекарств контролируют по небольшой выборке и сравнивают с нормой; тогда нулевая гипотеза H 0 : выпущенная партия лекарств нестандартна (брак), а конкурирующая H1 : партия соответствует норме .
Таким образом, задача проверки гипотез заключается в том, чтобы на основании анализа выборочных данных (неполная информация) принять решение о справедливости одной из гипотез .
§ 8.2. Ошибки первого и второго рода. Уровень значимости При проверке гипотез из-за наличия неполной информации могут быть допущены ошибки двух видов (см. таблицу 8.1):
Ошибка первого рода заключается в том, что верная нулевая гипотеза H 0 отвергается, а принимается конкурирующая ложная гипотеза H1 .
Ошибка второго рода заключается в том, что ложная гипотеза H 0 принимается, хотя на самом деле верна конкурирующая гипотеза H1 .
Отметим, что гипотезы H 0 и H1 в исследовании не равноправны .
Статистическая проверка осуществляется для нулевой гипотезы H 0, поэтому гипотезу H 0 и называют основной. Проверить нулевую гипотезу необходимо так, чтобы возможность ошибок обоих типов свести к минимуму .
Число – вероятность ошибки первого рода (вероятность отклонения нулевой гипотезы, когда она на самом деле верна) – называют уровнем значимости .
Аналогично вероятность допустить ошибку второго рода обозначим .
Вероятность не допустить ошибку второго рода (т.е. при справедливости конкурирующей гипотезы H1, вероятность принять эту гипотезу) называют мощностью критерия (чувствительностью критерия) .
Мощность критерия равна 1. Понятно, что чем больше это значение, тем лучше, качественнее работает наш критерий. В медицинских исследованиях обычно используют = 0,05 или = 0,01, а значение = 0,2 или = 0,1 .
Задача исследователя – минимизировать обе вероятности – и, и. Но эти вероятности оказываются взаимосвязанными и, уменьшая одну из них при фиксированных условиях, мы неизбежно компенсируем достигнутое уменьшение ростом вероятности другой ошибки. Единственный способ одновременного уменьшения вероятностей обеих ошибок – это увеличение объема выборки (вполне естественно, что, увеличивая объем выборки, получаем больше информации о генеральной совокупности, и вероятность ошибок уменьшается) .
Обычно поступают следующим образом: фиксируют уровень значимости, т.е. задают границу вероятности отклонить нулевую гипотезу H 0, когда она верна, и пытаются провести исследование так, чтобы значение оказалось наименьшим. Стандартными уровнями значимости, для которых построены соответствующие таблицы, считаются числа 0,2; 0,1; 0,05; 0,02; 0,01; 0,005; 0,002; 0,001 .
Естественным является желание выбрать как можно меньшим, но тогда вероятность ошибки второго рода может оказаться слишком большой (мощность критерия невелика). Разумный компромисс между значениями и находят, исходя из тяжести последствий каждой из ошибок. Например, пусть проверяется гипотеза отсутствия у пациента некоторого заболевания. Признаком заболевания служит значение определенного показателя (к примеру, артериальное давление), тогда нулевая гипотеза H 0 – значение показателя в норме, т.е. пациент здоров .
Конкурирующая гипотеза H1 – значение показателя отличается от нормы, т.е. пациент болен. В этом случае ошибка первого рода – отклонение нулевой гипотезы, когда она верна, т.е. признаем человека больным, когда он на самом деле здоров. Эта ошибка приводит к некоторым неудобствам для пациента, который должен пройти дополнительное обследование или курс лечения, и обычно не грозит серьезными последствиями. Совсем иная картина в случае допуска ошибки второго рода – принять нулевую гипотезу, когда она неверна, т.е. признать человека здоровым, когда он на самом деле болен: фактически происходит отказ от лечения больного, и в этом случае последствия ошибки второго рода могут оказаться самыми плачевными .
Следовательно, в рассмотренном примере допустимо пожертвовать высоким уровнем значимости с целью уменьшить вероятность ошибки второго рода. Можно привести примеры других случаев, когда, наоборот, более существенным по тяжести последствий оказывается выбор наименьшего разумного значения, а не .
Таким образом, при выборе гипотез нулевой гипотезой (по сравнению с альтернативной) должна быть та, которую более опасно ошибочно отвергнуть .
§8.3. Статистический критерий. Критические области Для проверки принятой гипотезы используют случайную величину K, являющуюся функцией от выборочных данных и называемую статистическим критерием .
Статистический критерий – это правило (формула), позволяющее по данным выборки принять либо отвергнуть нулевую гипотезу .
Статистический критерий, являясь случайной величиной, имеет какое-то вероятностное распределение. Обычно критерий выбирают таким, чтобы он имел одно из следующих распределений: нормальное,
-квадрат, распределение Стьюдента, распределение Фишера .
Совокупность значений, при которых нулевую гипотезу следует принять, называют областью принятия гипотезы. Совокупность значений, при которых нулевую гипотезу следует отвергнуть, называют критической областью .
Поскольку все возможные значения критерия К образуют интервал, то критическая область и область принятия гипотезы также являются интервалами. Эти интервалы не могут пересекаться и, следовательно, имеются граничные точки, разделяющие данные области .
Точки, отделяющие критическую область от области принятия гипотезы, называют критическими точками. Обозначим их kкр .
Рис. 8.1 Критическая область в зависимости от выбора kкр может быть односторонней (правосторонней или левосторонней) или двусторонней .
В случае, изображенном на рис. 8.1 (а), критическая область определяется неравенством K kкр, где kкр 0, и называется правосторонней .
В случае, изображенном на рис. 8.1 (б), критическая область определяется неравенством K kкр, где kкр 0, и называется левосторонней .
В случае, изображенном на рис. 8.1 (в), двусторонняя критическая область определяется двумя неравенствами K kкр1, K kкр 2 где kкр1 kкр 2. Часто двустороннюю критическую область выбирают симметричной относительно нуля, тогда (kкр1 ) = kкр 2 = kкр и K kкр .
Как видим, критическая область полностью определяется одним или двумя (в случае двусторонней и несимметричной областей) критическими значениями. И здесь возникают два вопроса, первый из которых – по какому принципу выбирать критическую область; второй – каким образом определить критические значения kкр ?
Принцип построения критической области таков: критическая область – эта область возможных значений критерия K, принимаемых крайне редко, т.е. достаточно мала вероятность, что в результате наблюдения за одной выборкой случайная величина K, созданная по этой выборке, примет значение из критической области. Обозначим эту вероятность попадания критерия K в критическую область символом (это значение является уровнем значимости) .
Тогда критическая область при выбранном малом значении определяется условием P( K kкр ) = в случае правосторонней критической области, P( K kкр ) = в случае левосторонней критической области. В случае двусторонней критической области P( K kкр1 ) + P( K kкр 2 ) = .
Заметим, что в последнем равенстве критические точки kкр1 и kкр 2 определяются неоднозначно. Если же распределение критерия К симметрично относительно нуля (например, распределение Стьюдента или нормальное распределение) и критические точки kкр1 = ккр 2 = ккр, то P( K kкр1 ) = P( K kкр 2 ) и, следовательно, имеем P( K kкр ) = P( K kкр ) = .
Определив критическую область, а, следовательно, и область принятия гипотезы, по выборке вычисляем наблюдаемое значение критерия
K. Из частотной интерпретации следует вывод:
– если значение K принадлежит области принятия гипотезы, то нулевая гипотеза H 0 не противоречит наблюдениям и принимается;
– если значение K принадлежит критической области, то нулевая гипотеза H 0 считается опровергнутой, и принимается конкурирующая гипотеза H1 .
В случае принятия нулевой гипотезы считается, что различия между наблюдёнными значениями и истинными обусловлены случайными причинами и являются незначимыми (непринципиальными) .
В случае отторжения нулевой гипотезы говорят, что различия между наблюдёнными значениями и теоретическими (согласно нулевой гипотезе) значимы, т.е.
обусловлены принципиальными причинами:
ошибочностью нулевой гипотезы .
Еще раз отметим, что опровержение гипотезы H 0 на основании опыта вовсе не равноценно логическому опровержению. Вполне возможно, что нам просто не повезло с выборкой: среди множества всех возможных выборок заданного объема n попалась именно такая редкая, которая приводит значение критерия K в критическую область .
Критерии бывают параметрические и непараметрические. Параметрические критерии используются, если выборки взяты из генеральной совокупности, которая подчиняется известному, например, нормальному закону распределения. Нормальность распределения выборки должна быть статистически доказана до применения параметрических критериев .
Непараметрические критерии используют, если нет подчинения распределения выборки нормальному закону. Например, если объём выборки настолько мал, что невозможно оценить закон распределения данных в выборке. Параметрические критерии являются более мощными, чем непараметрические в обнаружении реального эффекта .
Критерии общего характера проверки статистических гипотез называют критериями значимости. В случае проверки гипотез о согласии выборочного и теоретического распределений критерии значимости называют критериями согласия .
Процедура проверки гипотез
Процедура проверки гипотез представляет собой правило, руководствуясь которым, принимается статистически обоснованное решение о справедливости одной из них .
От исследователя, использующего статистическую проверку гипотез в прикладных задачах, требуется научиться пользоваться существующими критериями .
Проверка гипотез обычно проходит следующие этапы .
1. Исследователь набирает первичный статистический материал в виде выборок из одной или нескольких генеральных совокупностей .
2. Исследователь формулирует основную ( H 0 ) и альтернативную ( H1 ) гипотезы, а также выбирает уровень значимости (0,01 или 0,05), соответствующие целям исследования .
3. Выбирают метод проверки, который подходит в данной ситуации, и по соответствующим формулам вычисляют значение статистического критерия для имеющихся данных (выборок) .
4. По таблицам, соответствующим выбранному методу, находят границу критической области для принятого уровня значимости .
5. Принимается решение о справедливости гипотезы H 0 или H1 .
Если значение критерия, вычисленного в п.3, принадлежит критической области (п. 4), то основная гипотеза H 0 отвергается и принимается альтернативная гипотеза H1 (различия между наблюдаемыми значениями и теоретическими значимы, т. е. обусловлены ошибочностью нулевой гипотезы) .
Если значения критерия не попадают в критическую область, то гипотеза H 0 принимается (различия не значимы и обусловлены случайными причинами) .
В ходе проверки статистических гипотез, кроме вычисления статистического критерия K, в современных статистических пакетах вычисляется также соответствующее значение p, где p – это вероятность справедливости H 0 .
Сравнивая полученное значение p с принятым уровнем значимости, делают выводы о гипотезах:
если p ( – принятый уровень значимости, обычно 0,05), то H 0 принимают (различия незначимы);
если p, то H 0 отклоняют (различия статистически значимы при p 0,05 ) .
§ 8.4. Зависимые и независимые выборки. Сравнение дисперсий двух нормальных генеральных совокупностей .
Примеры независимых выборок:
1) параметры двух групп пациентов, к которым применялись различные методики лечения;
2) параметры двух групп пациентов, к одной из которых (опытная группа) применялось воздействие методики, а к другой, контрольной, – нет .
Примеры зависимых (связанных или сопряжённых выборок):
1) параметры одной и той же группы пациентов до и после воздействия какого-либо фактора, например, методики лечения;
2) параметры различных частей одного и того же объекта, например, состояние двух конечностей, одна из которых подвергалась лечению, а другая – нет .
Перейдем к рассмотрению некоторых наиболее популярных статистических гипотез, используемых в медицинских исследованиях, и примеров их использования .
Сравнение дисперсий двух нормальных генеральных совокупностей
Во многих клинических исследованиях важной является проверка гипотезы о равенстве генеральных дисперсий двух нормальных выборок. Эта задача может быть решена с помощью критерия Фишера .
Пусть имеются две нормальные генеральные совокупности X и Y, дисперсии которых D( X ) и D(Y ) неизвестны. По выборкам X1, X 2. X n и Y1, Y2. Ym объемов n и m соответственно требуется сравнить дисперсии. Подобные задачи возникают в случаях сравнения точности измерений, точности приборов, качества методик. Поскольку дисперсия характеризует степень сосредоточения (рассеяния) значений относительно среднего, то наилучшей характеристикой является та, у которой дисперсия меньше .
Из множества различных гипотез относительно дисперсий (соотношений между дисперсиями) в качестве нулевой гипотезы обычно выдвигают гипотезу равенства дисперсий:
Тогда для конкурирующей гипотезы остаются следующие возможности:
1) D( X ) D(Y ) ; 2) D( X ) D(Y ) ; 3) D( X ) D(Y ) .
Понятно, что случаи 2) и 3) принципиального различия в методике не имеют, так как любое из этих неравенств получается из другого, если X и Y поменять местами. Таким образом, достаточно рассмотреть два случая конкурирующей гипотезы .
В нулевой гипотезе Н 0 : D( X ) = D(Y ) числа D( X ) и D(Y ) заменим характеристиками, связанными с выборками:
D( X ) = M ( S x ), D(Y ) = M ( S y ), где S x и S y – исправленные выборочные дисперсии рассматриваемых генеральных совокупностей. Тогда Н 0 : M ( S x ) = M ( S y ) .
Для проверки нулевой гипотезы используем в качестве критерия статистику F отношения двух исправленных выборочных дисперсий S x и S y с (n 1) и (m 1) степенями свободы соответственно .
Для определенности условимся в отношении оценок и числителем ставить большую из этих оценок, а знаменателем – меньшую. Обозначив их Sб и S м, получим критерий Sб F= 2 .
Sм Далее достаточно выбрать уровень значимости а (например, наиболее распространенные в медицинских приложениях уровни значимости = 0,05 или 0,01) и по таблице определить критические точки распределения F. И здесь возникает вопрос, какую критическую область выбрать: одностороннюю либо двустороннюю. Наш выбор зависит от вида конкурирующей гипотезы H1. Если есть основания предполагать, что одна из дисперсий обязательно не меньше, чем другая, например D( X ) D(Y ), то Н 0 : D( X ) = D(Y ) ;
В этом случае критическая область односторонняя, а именно правосторонняя .
Если же нет оснований полагать, что одна из дисперсий обязательно больше, чем другая, то конкурирующая гипотеза Н1 : D( X ) D(Y ) и критическая область оказывается двусторонней, а, следовательно, уровень значимости должен быть поделен между двумя интервалами критической области .
Далее находим реальное значение F, наблюдаемое, а точнее, вычисляемое по выборочным данным. Обозначим его Fнабл. Если окажется, что Fнабл приняло значение из критической области, то нулевую гипотезу отбрасываем и принимаем конкурирующую, в противном случае, когда Fнабл оказывается в области принятия гипотезы, нулевую гипотезу принимаем и полагаем, что она не противоречит опытным данным .
Рассмотрим оба возможных случая конкурирующей гипотезы .
Первый случай:
Пусть Н 0 : D( X ) = D(Y ) ; Н1 : D( X ) D(Y ) .
• по выборкам X1, X 2. X n и Y1, Y2. Ym вычисляем конкретные значения исправленных выборочных дисперсий S x и S y ;
(при выбранной конкурирующей гипотезе D( X ) D(Y ), естественно, Sб = S x, S м = S y );
• выбираем уровень значимости и для правосторонней критической области находим по таблице (приложение 5) граничное значение: критическую точку kкр (при этом f1, f 2 — количество степеней свободы числителя и знаменателя соответственно);
• обозначим kкр = Fкр (; f1 = n 1, f 2 = m 1) ; сравниваем Fнабл и Fкр ;
• делаем выводы: если Fнабл Fкр, то при выбранном уровне значимости различие дисперсий значимо, нулевая гипотеза отбрасывается и принимается конкурирующая, если же Fнабл Fкр, то принимается гипотеза Н0 как не противоречащая опытным данным .
Второй случай:
Пусть Н 0 : D( X ) = D(Y ) ; Н1 : D( X ) D(Y ) .
• по выборкам X1, X 2. X n и Y1, Y2. Ym вычисляем конкретные значения исправленных выборочных дисперсий S x и S y ;
• выбираем уровень значимости и находим критическую точку kкр = Fкр ; f1, f 2 ;
• сравниваем Fнабл и Fкр и делаем выводы: если Fнабл Fкр, то при выбранном уровне значимости различие дисперсий значимо, нулевая гипотеза отвергается, если же Fнабл Fкр, то принимается гипотеза H 0 как не противоречащая опытным данным .
Пример 8.1 .
Пусть при лечении некоторого заболевания применяются две методики: А и В. Эффективность методик характеризуется изменением численных значений определенного показателя. Отобраны две однородные группы больных: первая численностью n = 15 человек, а вторая – m = 10 человек. В первой группе (с методикой А) значения рассмотренного показателя X1, X 2. X15, во второй (с методикой В) – Y1, Y2. Y10. Известно, что соответствующие генеральные совокупности X и Y имеют нормальное распределение. Оказалось, что для обеих групп средние значения показателя х и у практически равны, а исправленные выборочные дисперсии S x = 21,5 ; S y = 32,8. Требуется со
случайными причинами. Таким образом, статистически значимых различий методик не установлено .
§ 8.5. Сравнение средних двух нормальных генеральных совокупностей при известных дисперсиях Пусть имеются две генеральные совокупности X и Y. Исходя из выборочных данных, требуется сравнить математические ожидания M ( X ) и M (Y ) .
Подобная задача возникает при сравнении двух групп элементов, подвергшихся определенному воздействию (например, двух групп больных, проходящих курс лечения по различным методикам, или одна группа больных принимает какой-то лекарственный препарат, а другая группа – контрольная – принимает плацебо). При этом сравнение средних позволяет судить о степени воздействия, о значимости возможных эффектов воздействия или, наоборот, об их отсутствии .
Рассмотрим случай, когда генеральные совокупности X и Y имеют нормальное распределение, что в прикладных задачах бывает достаточно часто .
Данными для исследования будут служить две независимые выборки: X1, X 2. X n и Y1, Y2. Ym объемов n и m соответственно. Схема исследования – выдвижение гипотез, нулевой и конкурирующей, и использование статистики определенного вида в качестве критерия .
Нулевая гипотеза о равенстве математических ожиданий M ( X ) = M (Y ) равносильна гипотезе H 0 : M ( X ) = M (Y ) так как M ( X ) = M ( X ) и M (Y ) = M (Y ) ввиду несмещенности оценок математического ожидания. Поскольку значения выборочных средних X и Y, вообще говоря, различны, то необходимо проверить, значимо это различие (вызвано принципиальными соображениями) либо незначимо (вызвано случайными обстоятельствами, методами отбора именно этих, а не других элементов в выборку, малым количеством наблюдений) .
Критерием для проверки гипотезы H 0 может служить статистика X Y Z= .
2 Sy Sx + n m Вернемся к проверке выдвинутой нулевой гипотезы. Схема действий та же самая, что и в предыдущем разделе. В противовес H 0 назначается конкурирующая гипотеза H1. Далее по выборочным значениям вычисляем значение Z набл, выбираем уровень значимости и находим критическую точку. Критическое значение Z кр определяется соотношением:
1 Ф( Z кр ) = где Ф(z) – функция Лапласа (приложение 6) .
Сравниваем Z набл и Z кр и делаем выводы: если Z набл Z кр, то при выбранном уровне значимости различие дисперсий значимо, нулевая гипотеза отвергается, если же Z набл Z кр, то принимается гипотеза H 0 как не противоречащая опытным данным .
§ 8.6. Критерий Стьюдента .
Сравнение средних двух нормальных генеральных совокупностей при неизвестных одинаковых дисперсиях
где S x и S x – выборочные дисперсии, x и y – средние значения выборок .
Критическое значение tкр (, f = n + m 2) распределения Стьюдента находим по таблице (приложение 7) для заданного уровня значимости .
Сравниваем tнабл и tкр и делаем выводы: если tнабл tкр, то при выбранном уровне значимости различие дисперсий значимо, нулевая гипотеза отвергается, если же tнабл tкр, то принимается гипотеза Н0 как не противоречащая опытным данным .
Данный критерий применяется в случае малых выборок, что свойственно медицинским и биологическим задачам, а это обусловливает многочисленные приложения критерия Стьюдента .
Пример 8.2 .
Препарат из группы антагонистов кальция – нифедипин – обладает способностью расширять сосуды, и его применяют при лечении ишемической болезни сердца. Ш. Хейл и соавторы измеряли диаметр коронарных артерий после приёма нифедипина и плацебо, и получили следующие две выборки данных диаметра коронарных артерий (в миллиметрах) .
Плацебо: 2,5; 2,2; 2,6; 2,0; 2,1; 1,8; 2,4; 2,3; 2,7; 2,7; 1,9;
Нифедипин:2,5; 1,7; 1,5; 2,5; 1,4; 1,9; 2,3; 2,0; 2,6; 2,3; 2,2 .
Позволяют ли приведенные данные считать, что нифедипин влияет на диаметр коронарных артерий?
В данной задаче необходимо исследовать, значимо или незначимо различаются средние, представленные двумя выборками. Обозначим генеральную совокупность, из которой извлечена первая выборка (плацебо), через Х. Соответственно обозначим генеральную совокупность, из которой извлечена вторая выборка (нифедипин), через Y. Авторы полагали, что обе генеральные совокупности X и Y имеют нормальное распределение (эту гипотезу желательно проверить статистическими методами) .
По выборкам из обеих генеральных совокупностей вычислим соответствующие выборочные характеристики:
x = xi = (2,5 + 2,2 + 2,6 + 2,0 +. + 2,3 + 2,7 + 2,7 + 1,9) = 2,29;
11 i =1 11 y = y j = (2,5 + 1,7 + 1,5 + 2,5 +. + 2,0 + 2,6 + 2,3 + 2,2) = 2,08;
11 j =1 11 ( xi x )2 = 10 [(2,5 2,29)2 +. + (1,9 2,29)2 ] = 0,1009;
Sх = 11 1 i =1 ( y j y )2 = 0,1716 .
= 2 Sy 11 1 j =1 Поскольку выборки малого объема n = m = 11, для проверки значимости различий средних применим критерий Стьюдента. Для использования критерия необходимо иметь равные дисперсии: D( X ) = D(Y ) .
В нашем случае эти дисперсии неизвестны, но данное равенство можно проверить, воспользовавшись критерием Фишера о равенстве дисперсий. Нулевая гипотеза в критерии Фишера H 0 : D( X ) = D(Y ) .
В качестве конкурирующей гипотезы рассмотрим H1 : D( X ) D(Y ), откуда следует, что критическая область – двусторонняя. Уровень значимости полагаем стандартным = 0,05.
По таблице (приложение 5) находим критическую точку, исходя из равенства:
kкр = Fкр ; f1, f 2 = Fкр (0,025;10;10 ) = 3,72 .
2 Вычисляем Fнабл. Поскольку среди S х и S y большей дисперсией
та нулевая гипотеза M ( X ) = M (Y ), как не противоречащая опытным данным .
Вывод: В рассматриваемом примере критерий Стьюдента не выявил существенных различий в диаметрах коронарных артерий при сравнении двух групп обследуемых. Проведенный статистический анализ не позволяет считать значимым влияние нифедипина на диаметр коронарных артерий .
§ 8.7. Критерий знаков Пусть x1, x2. xn и y1, y2. yn – две группы значений, попарно связанных между собой. Критерий знаков является критерием проверки гипотезы об однородности этих групп наблюдений, точнее, о принадлежности их к одной и той же генеральной совокупности. Математически нулевая гипотеза H 0 состоит в равенстве соответствующих функций распределения: Fx = Fy. Вид альтернативной гипотезы H1 определяет критическую область:
• если H1 : Fx Fy, то критическая область двусторонняя;
• если H1 : Fx Fy, то критическая область левосторонняя;
• если H1 : Fx Fy, то критическая область правосторонняя .
Рассматриваемые выборки имеют попарно связанные элементы xi, yi, исходя из чего на практике критерий знаков используется для наблюдений до и после эксперимента. Исследуется наличие статистически значимого сдвига в значениях после эксперимента, которому и приписывается заслуга в этом изменении значений при справедливости гипотезы H1 и отсутствии значимого влияния на формирование значений при принятии гипотезы H 0 .
Отметим, что критерий знаков является непараметрическим, т.е .
может быть применен вне зависимости от распределения признака .
В критерии знаков рассматриваются соответствующие разности значений xi yi, но сама величина разности роли не играет, учитывается лишь знак выражения xi yi. В случае равенства какой-то из разностей нулю, эта пара наблюдений выводится из исследования. Таким образом, исходным пунктом для применения критерия оказывается последовательность знаков «+» и «–». Можно сравнивать, например, результаты клинических исследований у 2 групп больных, или у одних и тех же больных до и после лечения. Следовательно, критерий знаков применим и к случаю качественных изменений в наблюдениях типа «лучше – хуже», «больше – меньше» и т.д., что является его несомненным достоинством .
При справедливости нулевой гипотезы H 0 : Fx = Fy, означающей, что совокупности однородны, а преобладание знака «+»
или «–» в последовательности знаков является случайным, количества знаков «+» и «–» не должны существенно отличаться. Следовательно, для каждой пары наблюдений xi, yi появление того или иного знака происходит с вероятностью 0,5, а распределение случайной величины, принимающей значения от 0 до n, является биномиальным .
Пусть в серии из N опытов положительные значения Z наблюдались n+ раз, а отрицательные – n раз. Тогда проверка справедливости нулевой гипотезы сводится к проверке значимости отличия n+ или n от 0,5 .
В математической статистике показывается, что для такой проверки следует ввести еще одну величину nN, определяемую как наименьшее из чисел n+ или n, и сравнить ее со значением критического чискр ла nN .
кр Критические числа nN определяются объемом выборки N и уровкр нем значимости. В качестве критического числа nN следует принимать целую часть числа N 1 A= k N +1, где k = 0,8224 для = 0,10 и k = 0,9800 для = 0,05 .
кр Если nN nN, то нулевую гипотезу следует считать согласуюкр щейся с экспериментом. Если nN nN, то нулевую гипотезу отвергают .
Недостатком критерия знаков является то, что он учитывает только знак разностей сравниваемых наблюдений, не отражая величины этой разности. Поэтому критерий знаков имеет ограниченную мощность .
Пример 8.3 .
Проведено 100 опытов по изучению влияния некоторого физического фактора на величину артериального давления у двух групп животных, причем от опыта к опыту уровень фактора изменялся и регистрировались различия артериального давления у двух животных (по одному из каждой группы). При уровне значимости = 0,05 оценить значимость различия в действии данного фактора на указанные группы животных, если в серии из 100 опытов положительная разность давлений наблюдалась 48 раз, а отрицательная – 44 раза .
В данном случае nN = 44. Находим критическое значение:
A= 0,98 100 + 1 = 39,6 кр кр следовательно, nN = 39. Поскольку nN nN, то отвергать нулевую гипотезу нет оснований, и при уровне значимости = 0,05 различие в действии изучаемого фактора на рассматриваемые группы животных можно считать незначимым .
§ 8.8. Критерий Манна – Уитни (критерий однородности) Для установления эффективности влияния некоторых факторов (лекарственного препарата, метода лечения, курения, занятия спортом и т. д.) на определенный контролируемый показатель ранее мы использовали критерий Стьюдента. В критерии Стьюдента мы рассматривали две выборки, извлеченных из нормальных генеральных совокупностей, и при условии равенства дисперсий (которое проверялось заранее) устанавливали, значимо или нет различие средних в этих генеральных совокупностях. Если это различие оказывалось незначимым, то, исходя из того, что нормальное распределение полностью определяется двумя параметрами (средним и дисперсией), мы делали вывод о совпадении этих генеральных совокупностей. Следовательно, можно считать, что обе выборки извлечены из одной и той же генеральной совокупности, т. е .
однородны. Если же выборочные средние различаются значимо, то выборки извлечены из разных генеральных совокупностей, тот есть неоднородны .
Непараметрическим аналогом критерия Стьюдента является критерий Манна – Уитни .
Сущность этого критерия в следующем. Рассматриваются две группы наблюдений. Требуется установить однородность этих групп, т. е. можно ли считать эти выборки полученными из одной и той же генеральной совокупности или они получены из различных генеральных совокупностей .
Порядок расчёта критерия Манна – Уитни следующий:
1) Данные обеих выборок объединяем в одну и упорядочиваем по возрастанию. Каждому элементу группы предписываем его ранг. При этом элемент, обладающий наименьшим значением, получает ранг 1, следующий – ранг 2 и т.д. Последний ранг N, где N = n + m – суммарный объем выборок, получает элемент, принимающий наибольшее значение .
Если несколько элементов имеют одинаковые значения, то всем им предписывается один и тот же ранг, равный среднему арифметическому номеров, под которыми стоят элементы в упорядоченной группе .
Например, после упорядочения группа на 3-м и 4-м месте оказались элементы с равными значениями, тогда ранг каждого из них равен 3,5 .
2) Присвоив элементам ранги, опять разводим их по своим группам. Вычисляем значение критерия Т, где Т – сумма рангов элементов меньшей из групп .
Замечание. С тем же успехом, если условиться, можно вычислять Т как сумму рангов элементов большей из групп. Эта условность не принципиальна. В случае равного количества элементов в группах берем любую .
3) Вводим нулевую гипотезу об однородности двух выборок .
4) Полученное наблюдаемое значение критерия Т сравниваем с двумя критическими значениями, взятыми из соответствующей таблицы (приложение 8, 9). Если наблюдаемое значение Т находится между полученными критическими значениями, то принимаем нулевую гипотезу:
выборки извлечены из одной генеральной совокупности .
Пример 8.4 .
Исследуется эффективность препарата, позволяющего сбросить лишнюю массу больным, страдающим ожирением. При этом группе добровольцев предписана определенная диета. Через месяц подобного режима, соблюдения диеты и регулярного приема препарата фиксируется величина потерянной массы в килограммах. Для проведения эксперимента отобрана группа из 8 добровольцев, причем 3 их них действительно получали исследуемый препарат (экспериментальная группа), а 5 довольствовались плацебо (контрольная группа). Отбор 3 добровольцев из 8 в экспериментальную группу осуществлялся случайным образом (репрезентативно) .
Полученные данные проранжированы и занесены в таблицу
В таблице указана сумма рангов элементов меньшей из групп:
Нулевая гипотеза для двух рассматриваемых выборок – однородность групп, т. е. утверждение, что обе полученные выборки рангов извлечены из одной генеральной совокупности, а, следовательно, препарат неэффективен. Для проверки (или опровержения) этой гипотезы найдем критические точки .
Эти критические точки равны 6 и 21 при уровне значимости = 0,036 и равны 7 и 20 при уровне значимости = 0,071. В таблице приведены критические точки при двух значениях, так как оба этих значения, 0,036 и 0,071, близки к стандартному уровню значимости = 0,05 .
Наше наблюдаемое значение критерия Т = 17,5, находится между критическими точками. Это означает, что отвергнуть нулевую гипотезу о неэффективности препарата нет оснований: исследуемый препарат неэффективен, а снижение массы объясняется другими причинами, возможно, диетой. Если обратиться к таблице данных, то заметно, что в экспериментальной группе наблюдается превышение значений потерянной массы над соответствующими значениями в контрольной группе. Однако то, что мы предполагаем интуитивно, статистический критерий не выявил по причине слишком малого объема выборки .
§ 8.9. Критерий Уилкоксона (наблюдения до и после эксперимента) Критерий Уилкоксона является еще одним непараметрическим аналогом критерия Стьюдента. Поскольку критерий непараметрический, то для его применимости не требуется какой-либо определенный закон распределения генеральной совокупности. Критерий Уилкоксона – ранговый критерий, причем присваиваемые значениям признака ранги могут быть как положительными, так и отрицательными .
При применении критерия Уилкоксона для одних и тех же объектов наблюдения снимаются дважды: до эксперимента и после эксперимента. Под экспериментом понимается некоторое воздействие на объект, в результате которого наблюдаемые показатели могут измениться в ту или иную сторону: например, прием лекарственного препарата или определенная методика лечения приводят к некоторым изменениям контролируемых показателей. Задача критерия – по статистическим данным установить эффективность воздействия .
Группа наблюдений до эксперимента выступает в роли контрольной группы, а группа наблюдений после эксперимента – в роли экспериментальной группы .
В качестве наблюдаемого значения будем использовать разность наблюдаемых показателей до и после эксперимента для каждого индивидуума. Таким образом, из двух групп наблюдений получается одна выборка значений, среди которых могут быть как положительные (уменьшение показателя), так и отрицательные (увеличение показателя). При нулевой разности наблюдение не учитывается .
Далее производится ранжирование этой выборки, причем несколько иначе, чем в критерии Манна – Уитни, где используется простое упорядочивание. В нашем случае, прежде чем приступить к упорядочиванию выборочных значений, их вначале заменяют соответствующими абсолютными величинами, а затем полученные положительные числа ранжируют по возрастанию. Расставленные таким образом ранги изменения показателя являются промежуточными, далее каждому такому рангу предписывается знак «+» или «–» в зависимости от знака соответствующей ему разности. Часть рангов окажется положительными числами, а другая часть – отрицательными. Такие ранги называют знаковыми. Сумма знаковых рангов – случайная величина W, называемая критерием Уилкоксона .
В случае, когда исследуемое воздействие неэффективно, количество положительных и отрицательных разностей (а также и знаковых рангов) в среднем должно уравновешиваться, так как нет превуалирующего изменения показателя в ту или иную сторону. Следовательно, среднее значение критерия Уилкоксона W должно быть равно нулю ( M (W ) = 0 – нулевая гипотеза) .
Для конкретной выборки разностей вычисляем Wнабл, по приложению 10 находим соответствующие критические точки (с учетом заданного уровня значимости ) и определяем принадлежность Wнабл критической области или области принятия нулевой гипотезы .
Пример 8.4 .
Выявляется эффективность специальной диеты, позволяющей избавиться от избыточного массы. Фиксируется масса каждого участника до начала эксперимента и через месяц соблюдения диеты. Данные для группы из пяти добровольцев представлены в таблице .
В первом столбце таблицы проставлен номер участника эксперимента, второй и третий столбцы представляют данные наблюдений массы в килограммах до и после эксперимента. Оставшиеся четыре столбца таблицы заполнены на основании этих данных. Уменьшение (изменение) показателя массы – это случайная величина, которую мы обозначаем X. Значения, представленные в соответствующем столбце
– выборка из генеральной совокупности X .
В нашем случае распределение X неизвестно, и для получения выводов мы используем другую случайную величину W – сумму знаковых рангов, которые получаются на основании сравнения различных значений случайной величины X с учетом положительности и отрицательности (т. е. знаков) этих значений. В последнем столбце выписаны значения знаковых рангов, сумма которых и есть наблюдаемое значение случайной величины W, выступающей в роли критерия. В нашем примере наблюдаемое значение критерия Wнабл = 13 .
Напомним, что нулевая гипотеза H 0 : M (W ) = 0 – теоретическое предположение и, следовательно, отклонение наблюдаемого значения W от теоретического среднего составляет 13 единиц (т.к. Wнабл = 13 ) .
Необходимо ответить вопрос о значимости этого отклонения:
можно ли считать, что это несоответствие вызвано случайными причинами или же существенное влияние оказывает диета питания .
По приложению 10 для n = 5 и уровне значимости = 0,062 критическое значение равно Wкрит = 15 .
Поскольку Wнабл Wкрит, то при уровне значимости = 0,062 принимается нулевая гипотеза H 0 : M (W ) = 0 .
§ 8.10. Критерии согласия 2 Критерием согласия называют критерий проверки гипотезы о предполагаемом законе распределения. Другими словами, критерии согласия призваны дать ответ на вопрос: отклонение эмпирических данных от соответствующих теоретических вызвано случайными обстоятельствами, например малым объемом выборки, или это расхождение существенно?
Имеется несколько критериев согласия: Пирсона, Колмогорова, Смирнова и др. Рассмотрим критерий согласия Пирсона, называемый также критерием хи-квадрат (2) .
Пусть по выборке объема получено эмпирическое распределение:
i =1 npi Рассмотрим конкретный пример применения критерия согласия .
Пример 8.5 .
При уровне значимости = 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические mi и теоретические частоты npi .
Так как 2 2, то нет оснований отвергнуть нулевую гипотенабл кр зу. Другими словами, расхождение эмпирических и теоретических частот незначимое. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности .
Рассмотрим применение множественных сравнений на примере сравнения эффективности различных препаратов, результатом применения которых является численное значение определенного показателя (среднее артериальное давление, уровень глюкозы плазмы, время лечения и т. д.). Для эксперимента отобраны случайным образом несколько групп больных. И каждая группа получила не разные препараты, а плацебо.
Результат применения такого «лекарства» нам заранее известен:
все групповые средние различаются незначимо просто по определению плацебо; все выборки оказываются извлеченными из одной и той же генеральной совокупности, и для каждой выборки оцениваемое генеральное среднее едино .
На практике проведенный подобным образом эксперимент чисто математически может указать на значимое различие выборочных средних для какой-то пары наблюдаемых групп, на основании чего вполне реально получить неверный результат о различном влиянии плацебо в разных группах. И чем больше будет исследуемых групп, т. е. больше пар выборок, тем чаще будет встречаться подобная ситуация, противоречащая здравому смыслу. Появление такого факта называют эффектом множественных сравнений .
Рассмотрим подробнее, в чем же причина возникновения эффекта множественных сравнений. Вспомним определение уровня значимости. Если у нас справедлива нулевая гипотеза о равенстве средних, то малое число – вероятность отвергнуть эту верную гипотезу. При этом число столь мало, что в единичном испытании нулевая гипотеза практически не отвергается. Сравнивая выборки попарно, мы проводим не одно, а большее количество испытаний и фактически увеличиваем вероятность отвержения верной гипотезы .
Уровень значимости – вероятность отвергнуть верную нулевую гипотезу, тогда вероятность противоположного события – принять верную нулевую гипотезу – равна 1. Если проводится k попарных сравнений, то вероятность все k раз принять верную нулевую гипотезу оказывается равной (1 ) k. Следовательно, вероятность противоположного события – хотя бы раз ошибиться – это 1 = 1 (1 ) k .
Пусть – стандартное значение уровня значимости, равное 0,05 .
Тогда для трех групп требуется три попарных сравнения (k = C3 = 3), и вероятность хотя бы одной ошибки равна 1 (1 0,05)3 0,143. Следовательно, по сравнению с = 0,05 вероятность ошибки выросла почти втрое. При сравнении четырех групп (k = C4 = 6), и тогда вероятность ошибки хотя бы при одном сравнении равна 1 (1 0,05)3 0,143. Это и есть объяснение появления эффекта множественных сравнений .
Оценим вероятность появления ошибки хотя бы в одном сравнении.
Если в выражении 1 (1 ) k для вероятности ошибки произвести упрощение, то окажется при разных k :
k = 2, 1 = 1 (1 ) 2 = 2 2 2 ;
k = 3, 1 = 1 (1 )3 = 3 3 2 + 3 = 3 2 (3 ) 3 ;
Последнее неравенство 1 k называют неравенством Бонферрони. Согласно этому соотношению, при числе парных сравнений k уровень значимости следует выбирать таким, чтобы 1, также оказывалось достаточно малым числом. Например, если мы хотим при трех сравнениях 1, т. е. вероятность ошибиться хотя бы раз, иметь не более чем 0,05, то необходимо в каждом сравнении проверять нулевую 0,05 гипотезу при = 0,0165 .
Величина уровня значимости = 1, где 1, выбирается заранее, k называют поправкой Бонферрони. Обычно поправку Бонферрони используют при малых значениях k, т. е. при небольшом количестве групп, так как тогда значение не является чересчур малым, что могло бы повлиять в реальной задаче на рост вероятности ошибки второго рода .
Критерий Фридмана является непараметрическим критерием, предназначенным для проверки однородности статистических данных .
При использовании данного критерия каждый объект ровно один раз подвергается каждому методу обработки (или наблюдается в фиксированные моменты времени). Результаты наблюдения упорядочиваются .
Причем отдельно упорядочиваются значения для каждого объекта независимо от всех остальных. Таким образом, получается столько упорядоченных рядов (блоков), сколько объектов участвует в исследовании .
Далее, для каждого метода обработки2 (уровня главного фактора) вычисляется сумма рангов. Если разброс сумм велик – различия статистически значимы .
Для применения критерия Фридмана столбцы таблицы данных должны отражать различные значения главного фактора (обработки), а строки (блоки) соответствуют повторным измерениям одного и того же объекта .
Пусть главный фактор принимает k различных значений, а мешающий фактор – n различных значений.
Тогда таблица данных будет иметь следующий вид:
С помощью критерия Фридмана проверяют нулевую гипотезу о том, что влияние главного фактора (обработки) не является значимым .
Альтернативная гипотеза H1 заключается в том, что гипотеза H0 неверна .
Если гипотеза H 0 справедлива, то наблюдения внутри каждой строки таблицы данных распределены одинаково, при этом распределения наблюдений внутри любого столбца могут быть различными, если влияние мешающего фактора значимо .
Процедура состоит в упорядочивании (ранжировании) значений в каждой строке (ранги в каждой строке принимают значения от 1 до k – число сравниваемых обработок). Так, наблюдения первой строки получат ранги r11. r1k, а наблюдения второй строки получат ранги r12. r2 k и т.д., в результате чего наблюдение xij получит ранг rij. Значения rij изменяются от 1 до k, а соответствующая строка рангов представляет некоторую перестановку чисел 1, 2. k (предполагается, что среди элементов, стоящих в одной строке таблицы данных нет совпадающих, в противном случае следует использовать средние ранги) .
Критерий Фридмана имеет вид:
В статистике принята терминология, по которой уровни главного фактора называют обработками, а уровни мешающего фактора – блоками .
При справедливости гипотезы H 0 слагаемые в выражении для F с большой вероятностью невелики, и, следовательно, значение F сравнительно мало. Нарушение гипотезы H 0 приводит к возрастанию статистики Фридмана .
Критическое значение Fкр при выбранном уровне значимости и заданных n и k находятся по приложению 12. При больших значениях n статистика Фридмана приближенно распределена по закону 2 с k 1 степенями свободы .
Если Fнабл Fкр для выбранного уровня значимости и заданных n и k (или соответствующего числа степеней свобод), то нулевую гипотезу отклоняют .
Если Fнабл Fкр, то на выбранном уровне значимости нулевая гипотеза об однородности выборок принимается .
Пример 8.7 .
Имеем данные по содержанию фосфора (мг/100г) в каждом из четырех органов у некоторых групп обследуемых:
Пусть Хi обозначает i-ю генеральную совокупность. Известно, что m генеральных совокупностей X1, X 2. X m имеют нормальное распределение ( m 2 ).
При уровне значимости требуется проверить гипотезу о равенстве дисперсий рассматриваемых генеральных совокупностей (также говорят об однородности дисперсий):
H 0 : D( X1 ) = D( X 2 ) =. = D( X m ) .
Для проверки этой нулевой гипотезы взяты выборки одного и того же объема n каждая и вычислены исправленные выборочные дисперсии S12, S2. Sm, которые, как известно, имеют число степеней свободы f = n 1. Численные значения исправленных выборочных дисперсий соответственно обозначим s1, s2. sm .
называемую критерием Кочрена (Кохрана), где Smax – та из исправленных выборочных дисперсий, значение которой наибольшее .
Критическое значение распределения Кочрена K кр (, f, m) определяем по таблице (приложение 13) .
Если K набл К кр, то нулевая гипотеза принимается, в противном случае K набл К кр делаем вывод, что дисперсии в рассматриваемых генеральных совокупностях различны. Уточнить, в каких именно генеральных совокупностях различаются дисперсии, можно с помощью того же или другого критерия, сравнивая меньшее количество выборок, например сравнивая выборки попарно .
В случае справедливости гипотезы Н0 в качестве оценки генеральной дисперсии используют среднее арифметическое значение имеющихся m исправленных выборочных дисперсий .
Пример 8.8 .
Три лаборатории провели анализ 9 проб исследуемого препарата для определения в нем процентного содержания эфирного масла. Исправленные выборочные дисперсии оказались: в первой лаборатории s1 = 0,037, во второй лаборатории s2 = 0,063, в третьей лаборатории s3 = 0,052. Предполагая, что случайная величина – процентное содержание эфирного масла в препарате имеет нормальное распределение, требуется при уровне значимости = 0,01 проверить гипотезу об однородности дисперсий .
Процентное содержание эфирного масла в препарате – это случайная величина (генеральная совокупность). Для каждой из лабораторий рассматриваемая генеральная совокупность своя. Таким образом, имеются три генеральные совокупности X1, X 2, X 3, из которых извлечены по одной выборке одинакового объема n = 9.
По вычисленным значениям s1, s2, s3 проверим нулевую гипотезу однородности дисперсий:
Пусть имеется m нормальных генеральных совокупностей. Обозначим их X1, X 2. X m. При уровне значимости требуется проверить нулевую гипотезу о равенстве соответствующих генеральных дисперсий:
H 0 : D( X1 ) = D( X 2 ) =. = D( X m ), называемую также гипотезой об однородности дисперсий .
Из каждой генеральной совокупности X i извлечена выборка объема ni. Если все ni равны, то для проверки Н0 можно использовать критерий Кочрена. В противном случае, когда выборки, вообще говоря, разного объема, нам необходим другой критерий проверки нулевой гипотезы. Рассмотрим критерий Бартлетта .
Пусть по выборкам найдены исправленные выборочные дисперсии S12, S2. Sm, при этом каждая статистика Si2 имеет число степеней
s2 = 0,033, s3 = 0,040 .
Предполагая, что процентное содержание эфирного масла в данном препарате имеет нормальное распределение, требуется при уровне значимости = 0,01 проверить гипотезу об однородности дисперсий .
Процентное содержание эфирного масла в препарате – случайная величина, т.е. генеральная совокупность, своя персональная для каждой лаборатории. Поскольку объемы выборок для каждой генеральной совокупности различны, для проверки гипотезы Н0, равенства генеральных дисперсий воспользуемся критерием Бартлетта .
Так как используется много данных, оформим их в виде таблицы:
1. Что такое статистическая гипотеза?
2. Какая гипотеза называется простой?
3. Дайте определение нулевой, альтернативной гипотезам .
4. В чем заключается задача проверки гипотез?
5. Какие могут возникнуть ошибки при проверки гипотез? Дайте определение ошибкам первого рода и ошибкам второго рода .
6. Что такое уровень значимости? Как он связан с доверительной вероятностью?
7. Что такое статистический критерий? Почему во многих исследованиях используют двусторонний критерий?
8. Что такое критическая область?
9. В чем заключается основной принцип проверки статистических гипотез?
10. Дайте определение односторонней критической области (двусторонней критической области) .
11. Когда используются параметрические, непараметрические критерии?
12. Какова процедура проверки гипотез?
13. Приведите примеры независимых, зависимых выборок .
14. В чем заключается проверка гипотез относительно средних?
15. Дайте понятие критерия Стьюдента (запишите формулу) .
16. Дайте определение критерия Фишера (запишите формулы, когда применяется данный критерий) .
17. В каком случае применяется критерий Манна–Уитни?
18. Дайте понятие критерия Уилкоксона .
19. В чем заключается критерий Краскела–Уоллиса?
20. При каких условиях применяется критерий Фридмана?
21. Дайте понятие критерия знаков .
22. Когда для проверки соответствующих гипотез можно использовать критерий Кочрена? Запишите формулы .
23. В каком случае для проверки гипотез можно использовать критерий Бартлетта? Запишите соответствующие формулы .
1. По двум независимым малым выборкам объемов n1 = 5 и n2 = 6, извлеченным из нормальных генеральных совокупностей X1 и X 2, найдены выборочные средние х1 = 33, х2 = 2,48. Известно, что генеральные дисперсии примерно равны, то есть x 2 = x 2. При уровне значимости = 0,05 проверить нулевую гипотезу H 0 : M ( X1 ) = M ( X 2 )
2. По двум независимым выборкам объемов n1 = 12 и n2 = 15, извлеченным из нормальных генеральных совокупностей X1 и X 2, найдены исправленные выборочные дисперсии S x 2 = 11,41 и S x 2 = 6,52 .
При уровне значимости = 0,05 проверить нулевую гипотезу о равенстве генеральных дисперсий H 0 : x 2 = x 2 .
3. По двум независимым малым выборкам объемов n1 = 5 и n2 = 6, извлеченным из нормальных генеральных совокупностей X1 и X 2, найдены выборочные средние х1 = 8,3, х2 = 7,48 и выборочные дисперсии S x 2 = 0,25 и S x 2 = 0,108. При уровне значимости = 0,05 проверить нулевую гипотезу H 0 : M ( X1 ) = M ( X 2 ) .
4. Средняя продолжительность госпитализации 36 больных пиелонефритом, получивших правильное, соответствующее официальным рекомендациям лечение, составила 4,51 суток, а 36 больных, получивших неправильное лечение, – 6,28 суток. Средние квадратические отклонения для этих групп – 1,98 суток и 2,54 суток соответственно. Значимо ли статистически различие в сроках госпитализации? Другими словами, способствует ли соблюдение официальных схем лечения сокращению госпитализации?
5. Были исследованы две независимые выборки объемом 60 больных каждая, перенесших операцию на сердце. Использовались два способа анестезии. У больных первой выборки (первый способ анестезии) минимальное среднее динамическое давление составило х1 = 66,9 мм рт. ст., а среднее квадратическое отклонение равно S1 = 12,2 мм рт. ст. У больных второй группы (в качестве наркоза использовался препарат №2) х2 = 73,2 мм рт. ст., а S2 = 14,4 мм рт. ст. Действительно ли препарат №1 в большей степени снижает артериальное давление? Оценить статистическую значимость различия средних и дисперсий .
6. Для проверки эффективности нового лекарственного препарата А отобраны две группы больных. Одна группа ( n1 = 50 человек) контрольная, которая получала плацебо, а вторая группа ( n2 = 70 человек) получала препарат А. Среднее значение некоторого гемодинамического показателя составило х1 = 78,5 в первой группе и х2 = 85 – во второй .
Дисперсии в группах равны соответственно x 2 = 100 и x 2 = 74. При уровне значимости = 0,05 выяснить, действительно ли препарат эффективен?
7. При исследовании влияния курения на развитие ишемической болезни сердца изучалась агрегация тромбоцитов. 111 добровольцев выкуривали по сигарете. До и после курения у них были взяты пробы крови и определена агрегация тромбоцитов. Используя критерий знаков, получили следующие результаты: 86 разностей – положительные, 4 – нулевые, 20 – отрицательные. Критическое значение критерия 44,5 при =0,05. Можно ли сказать, что изменение агрегации тромбоцитов статистически значимо или нет?
8. При анализе препарата дифференциальным методом по двум независимым выборкам объемов n1 = 11 и n2 = 14, извлеченным из нормальных генеральных совокупностей X1 и X 2, получены исправленные выборочные дисперсии S x 2 = 0,76 и S x 2 = 0,38. При уровне значимости = 0,05 проверить нулевую гипотезу о равенстве генеральных дисперсий .
9. По двум независимым выборкам, объемы которых n1 = 14 и n2 = 10, извлеченных из нормальных генеральных совокупностей X1 и X 2, найдены исправленные выборочные дисперсии летальных доз двух препаратов S x 2 = 0,84 и S x 2 = 2,52. При уровне значимости = 0,05 проверить нулевую гипотезу о равенстве генеральных дисперсий H 0 : x 2 = x 2, при конкурирующей гипотезе: H1 : x 2 x 2 .
10. При анализе вещества двумя способами по двум независимым выборкам объемов n1 = 10 и n2 = 8, извлеченным из нормальных генеральных совокупностей X1 и X 2, найдены выборочные средние х1 = 142,3 и х2 = 145,3 и исправленные дисперсии S x 2 = 2,7 и S x 2 = 3,2 .
При уровне значимости = 0,05 проверить:
1) равенство дисперсий по критерию Фишера;
2) проверить нулевую гипотезу: H 0 : M ( X1 ) = M ( X 2 ) .
11. Установлено, что средняя масса таблетки сильнодействующего лекарства должна быть равна 0,50 мг. Выборочная проверка 121 таблетки полученной партии лекарства показала, что средняя масса таблетки этой партии х = 0,53 мг. Требуется при уровне значимости = 0,01 проверить нулевую гипотезу H 0 : M ( X ) = 0,50 при конкурирующей гипотезе H1 : M ( X ) 0,50, где масса таблетки – генеральная совокупность X. Многократными предварительными опытами по взвешиванию таблеток, поставляемых фармацевтической фирмой, было установлено, что масса таблеток распределен нормально со средним квадратическим отклонением = 0,11 мг .
12. При исследовании продолжительности отрицательного времени при пробе на остроту зрения в двух группах учеников – мальчиков и девочек в возрасте 12 лет – были получены следующие результаты: у мальчиков х = 70 с, S x = 5 c при n = 20 наблюдениях; у девочек y = 75 с, S y = 6 c при m = 30 наблюдениях. Требуется определить, существенна ли разность средних в двух выборках. Уровень значимости принять равным = 0,05 .
13. Исследуется эффективность прививки против сыпного тифа .
Под наблюдением находится 17 685 человек. Наблюдаемые результаты занесены в таблицу .
Используя критерий 2, сделайте выводы об эффективности прививок .
14. Сравниваются методы лечения некоторого заболевания, применяемые в государствах А и В. Показателем эффективности лечения является разница в смертности больных, находящихся на излечении .
Данные смертности этих больных в течение определенного срока после установления диагноза приведены в таблице. По имеющимся данным требуется установить наличие (или отсутствие) существенной разницы в смертности больных в государствах А и В. Уровень значимости стандартный = 0,05 .
Указание. Заполните пустые графы таблицы. Для вычислений используйте критерий 2 .
§ 9.1. Функциональная, статистическая и корреляционная зависимости. Уравнение линейной регрессии Выявление статистических связей между случайными величинами широко используется в медицинской практике. Этим методом решаются задачи установления обоснованного диагноза, оценки эффективности лечения. Установление зависимости между различными показателями состояния больного и влияние их изменений на жизнедеятельность организма является важной задачей лабораторных и клинических исследований. Более того, все системы, органы, ткани, клетки целостного организма находятся в связи друг с другом; эту связь можно измерить, например, с помощью коэффициента корреляции. Благодаря различным формам корреляции организм проявляется как единая сложная целостная система .
Как известно, случайные величины X и Y могут быть либо независимыми, либо зависимыми. Зависимость случайных величин также подразделяется на функциональную и статистическую. Функциональная зависимость между двумя переменными существует в том случае, когда каждому допустимому значению одной из них соответствует одно вполне определенное значение другой. Функциональные зависимости иногда можно выразить аналитически. Так, например, объем шара зависит от его радиуса V = R3, площадь квадрата от его стороны S = a 2 .
В общем случае функциональная зависимость выражаются формулой y = f (x). Функциональная связь свойственна неслучайным (детерминированным) переменным .
В медико-биологических исследованиях чаще встречаются статистические зависимости между величинами. При этом каждому значению одной величины соответствует не единственное значение другой величины, а некоторое множество значений с определенным законом распределения. Например, между возрастом и ростом детей связь выражается в том, что каждому значению возраста соответствует определенное распределение роста (а не одно единственное значение). При этом с увеличением возраста (до определенных пределов) возрастает и среднее значение роста .
Частным случаем статистической зависимости между X и Y является корреляционная зависимость, когда каждому значению Х ставится в соответствие математическое ожидание (среднее арифметическое значение) распределения другой величины Y .
Корреляционной является зависимость массы тела от роста: каждому значению роста (X) соответствует множество значений массы (Y), причем, несмотря на общую тенденцию, справедливую для средних:
большему значению роста соответствует и большее значение массы тела, в отдельных наблюдениях субъект с большим ростом может иметь и меньшую массу. Корреляционной будет зависимость заболеваемости от воздействия внешних факторов, например запыленности, уровня радиации, солнечной активности и т.д. Имеется корреляция между дозой ионизирующего излучения и числом мутаций, между пигментом волос человека и цветом глаз, между показателями уровня жизни населения и процентом смертности, между количеством пропущенных студентами лекций и оценкой на экзамене. Именно корреляционные зависимости наиболее часто встречаются в природе в силу взаимовлияния и тесного переплетения огромного множества самых различных факторов, определяющих значения изучаемых показателей .
При установлении корреляционной зависимости экспериментально для каждого обследуемого объекта получают соответствующие пары значений величин Х и Y (например, роста и массы тела людей определенного пола и возраста):
Таблица 9.1 Значения величины Х x1 x2 x3 … xn Значения величины Y y1 y2 y3 … yn Пусть имеется выборка объемом n .
Каждой паре значений ( xi, yi ) на плоскости соответствует одна точка. Всего будет n точек. Область на графике y (x), занятая этими точками, образует поле корреляции или корреляционное поле точек .
По характеру расположения точек на нем можно сделать вывод о наличии или отсутствии корреляционной зависимости между величинами Y и Х. (табл. 9.2) Корреляционную зависимость можно описать с помощью уравнения вида M (Yx ) = f ( x), где M (Yx ) – условное математическое ожидание величины Y, соответствующее данному значению х; х – отдельные значения величины Х;
f (x) – некоторая функция .
Уравнение M (Yx ) = f ( x) называют уравнением регрессии Y на X, а его график называют линией регрессии .
а) Наличие линейной корреляционной зависимости
б) Неочевидная корреляционная зависимость
в) Наличие нелинейной корреляционной зависимости Обратную корреляционную зависимость (если она существует) можно описать уравнением регрессии Х на Y:
M ( X y ) = ( y ), где M ( X y ) – условное среднее значение величины Х, соответствующее данному значению у; ( y ) – некоторая функция .
Если функции f (x) и ( y ) – линейные функции, что можно оценить по характеру расположения точек корреляционного поля, то эти функции можно представить в виде:
M (Yx ) = ax + b = (наклон) ( х) + (сдвиг ), M ( X y ) = сy + d = (наклон) ( y ) + (сдвиг ) .
Данные формулы называются уравнениями прямой линейной регрессии .
Для нахождения коэффициентов a (наклон) и b (сдвиг), входящих в уравнение прямой, используем метод наименьших квадратов .
§ 9.2. Оценка параметров линейной регрессии по несгруппированным данным. Метод наименьших квадратов При проведении современных клинических исследований обычно нет недостатка в информации: каждому пациенту соответствует целое множество различных клинических показателей и данных. В них могут быть завуалированы некоторые соотношения, основные черты которых и позволяют выявлять методы регрессионного анализа. При этом задача регрессионного анализа состоит в подборе упрощенной аппроксимации этой связи с помощью математической модели .
Регрессионный анализ имеет в своем распоряжении специальные процедуры проверки, является ли выбранная математическая модель адекватной для описания имеющихся данных .
Чаще всего регрессионный анализ используется для прогноза, то есть предсказания значений ряда зависимых переменных по известным значениям других переменных .
Выше указывалось, что результаты наблюдений, приведенные в двумерной выборке, можно представить в виде корреляционного поля точек, где каждая точка соответствует отдельным значениям Х и Y. В результате получается диаграмма рассеяния, позволяющая судить о форме и тесноте связи между варьирующимися признаками. Довольно часто эта связь может быть аппроксимирована прямой линией (рис. 9.1)
Пример 9.1 .
Исследуется зависимость площади пораженной части легких у людей, заболевших эмфиземой легких, от числа лет курения .
Получены следующие данные:
Таблицу 9.5 можно рассматривать как зависимость условного среднего значения величины Y от величины Х, т .
е. как экспериментальную корреляционную зависимость .
Если построить точки ( xi, y xi ) в прямоугольной системе координат, то характер расположения этих точек может привести к предположению о форме корреляционной зависимости величины Y от Х в генеральной статистической совокупности .
Аналогично можно с помощью корреляционной таблицы для каждого значения y j величины Y составить таблицу эмпирического распределения величины Х (табл. 9.6) .
Построив в прямоугольной системе координат точки (Y ; Х y ), по характеру их расположения можно определить форму корреляционной зависимости величины X от Y, если эта зависимость наблюдается .
Таким образом, составление корреляционной таблицы и на основании ее таблиц типа 9.4 и 9.5, 9.6 и 9.7, а также графическое изображение полученных результатов позволяет высказать предположение о той или иной форме (например, линейной или квадратической) корреляционной зависимости величины Y от величины X и наоборот .
Задача корреляционного анализа заключается в обосновании силы и тесноты корреляционной связи. Задачей же регрессионного анализа является обоснование формы зависимости между Х и Y (линейная, криволинейная) .
Исторически теорию корреляции в биологии стали применять раньше, чем в других областях естествознания. Французский биолог Ж. Кювье в 1800-1805 годах в «Лекциях по сравнительной анатомии» сформулировал известный принцип биологической корреляции: любая часть организма непременно согласована с другими частями, следовательно, по одному органу можно судить о целом организме. В 1899 году англичанин К. Пирсон – создатель математической теории корреляции – вывел формулу, связывающую рост современного человека с длиной его бедра. Используя эту формулу, по длине ископаемого бедра Пирсон определил рост доисторического человека .
Для характеристики формы уравнения связи, в первую очередь необходимо учитывать теоретические соображения относительно характера связи между рассматриваемыми величинами. Характер расположения точек корреляционного поля позволяет делать вывод о форме связи. Вытянутая форма корреляционного поля и угол с осями графика, близкий к 450, указывает на наличие линейной корреляционной зависимости (рис. 9.3 г, д). Если же скопление точек образует круг или эллипс, длинная ось которого параллельна одной из осей координат, то можно предположить, что линейная корреляционная зависимость между величинами не просматривается (рис. 9.3 а) .
Основные свойства выборочного коэффициента корреляции
1. Коэффициент корреляции двух величин, не связанных линейной корреляционной зависимостью, равен нулю .
2. Коэффициент корреляции двух величин, связанных линейной корреляционной зависимостью, равен 1 в случае возрастающей зависимости и -1 в случае убывающей зависимости .
3. Абсолютная величина коэффициента корреляции двух величин, связанных линейной корреляционной зависимостью, удовлетворяет неравенству r 1. При этом коэффициент корреляции положителен, если корреляционная зависимость возрастающая, и отрицателен, если корреляционная зависимость убывающая .
4. Чем ближе r к единице, тем теснее корреляция между величинами Y, X .
По своему характеру корреляционная связь может быть прямой и обратной, а по силе – сильной, средней, слабой. Кроме того, связь может отсутствовать или быть полной (функциональной) .
§ 9.5. Проверка значимости коэффициента корреляции Коэффициент корреляции, как и любой другой выборочный показатель, служит оценкой своего генерального параметра. Выборочный коэффициент линейной корреляции rв – величина случайная, так как он вычисляется по значениям переменных, случайно попавшим в выборку из генеральной совокупности, а значит, как и любая случайная величина, имеет ошибку .
Чтобы выяснить, находятся ли случайные величины Х и Y генеральной совокупности в линейной корреляционной зависимости, надо проверить значимость rв. Для этого проверяют нулевую гипотезу о равенстве нулю коэффициента корреляции генеральной совокупности H 0 : r = 0, то есть линейная корреляционная связь между признаками X и Y случайна. Выдвигается альтернативная гипотеза H1 : r 0, то есть эта линейная корреляционная связь имеется. Задается уровень значимости, например, = 0,05 .
Критерием для проверки нулевой гипотезы является величина
tнабл :
rв n 2 tнабл = 1 rв 2 Далее по таблице критических значений распределения Стьюдента (см. приложение 7) при заданном уровне значимости (связанном с доверительной вероятностью соотношением = 1 ) и при числе степеней свободы f = n 2 находим критическое значение tкр для двусторонней критической области .
Затем сравнивают tнабл и tкр : если tнабл tкр, то при принятом уровне значимости делают вывод о значимости коэффициента корреляции (наличие корреляционной связи между признаками), в противном случае линейная связь может быть вызвана случайными факторами .
Если коэффициент корреляции оказывается значимым, то можно предсказать значение величины Y при любом значении X .
Замечание: Коэффициент корреляции характеризует связь между величинами, но не объясняет её. Наличие корреляции между Х и Y может быть вызвано тем, что: величина Х влияет на Y; величина Y влияет на Х;
на Х и Y влияет третий скрытый фактор, что создаёт впечатление связи между Х и Y (ложная корреляция) .
Рис. 9.4 Кроме того, если r = 0, то это не всегда говорит об отсутствии статистической связи между Х и Y – связь может быть и нелинейная (рис. 9.4) .
Пример 9.2 .
Имеется выборка из 10 наблюдений роста отцов (х) и их взрослых сыновей (y), см:
xi 180 172 173 169 175 170 179 170 167 174 yi 186 180 176 171 182 166 182 172 169 177
1. Установить, имеется ли корреляционная связь между величинами x и y .
2. Найти выборочный коэффициент корреляции r и определить тесноту корреляционной связи .
3. Записать уравнение регрессии .
4. Проверить, зависит ли рост взрослых сыновей от роста их отцов .
1. Построим корреляционное поле точек, отложив вдоль оси абсцисс величину роста отцов, а вдоль оси ординат – величину роста взрослых сыновей. Тогда каждой паре значений х и у на графике будет соответствовать определённая точка. По характеру расположения точек можно предположить существование линейной корреляционной связи между х и у .
По таблице находим величину tкр (0,05;8) = 2,31. Так как tнабл tкр, то есть 5,43 2,31, то делаем вывод о значимости коэффициента корреляции, т.е. рост взрослых сыновей зависит от роста их отцов .
Построим прямую регрессии внутри корреляционного поля:
Пример 9.3 .
В результате регистрации некоторых объектов определенного вида по заданным значениям признаков х и у получены числа (частоты) совпадений заданных значений этих признаков, помещенные в таблице.
По данным этой таблицы:
1) определить условные средние значения величин х и у, с их помощью получить изображение корреляционного поля и по характеру расположения точек на нем сделать вывод о типе линии регрессионной зависимости между величинами х и у;
2) найти коэффициенты регрессии у на х и х на у по методу наименьших квадратов;
3) составить уравнения прямых регрессии у на х и х на у;
4) вычислить коэффициент корреляции этих величин;
5) при уровне значимости = 0,05 проверить гипотезу о значимости выборочного коэффициента корреляции;
6) построить систему координат и в ней прямые регрессий .
Данные таблиц отражены на рисунке – корреляционном поле (крестики соответствуют данным первой таблицы, точки – данным второй таблицы) .
Как видно из рисунка, характер расположения построенных точек указывает на приблизительную линейную зависимость y x от х и x y от у.
Поэтому уравнения регрессии следует искать в виде:
y x = yx x + b, (*) x y = xy y + d, (**) где ух, xу – выборочные коэффициенты регрессии, составим вспомогательную расчетную таблицу для их нахождения.
Так как значения вариант признаков X и Y достаточно велики, то введем условные варианты u и v следующим образом:
Сх = 53, Су = 42 – варианты х и у, на которые приходятся условные варианты u=v=0. Напомним, что под вариантой мы понимаем наблюдаемое значение признака (см. §6.2) .
hх = 2, hу = 1 – длина интервалов вариации значений признаков х и у .
Далее по таблице критических значений распределения Стьюдента при заданном уровне значимости = 0,05 и числе степеней свободы f = n 2 = 20 2 = 18 находим критическое значение tкр для двусторонней критической области: tкр = 2,10 .
Так как tэксп tкр, можно сделать вывод о незначительности выборочного коэффициента корреляции .
Построим прямые регрессии внутри корреляционного поля:
1. Какая связь между Х и Y называется функциональной? статистической? корреляционной?
2. Что такое корреляционное поле?
3. Что такое регрессия? линия регрессии? Запишите соответствующие формулы .
4. В чем преимущество регрессии по сравнению с корреляцией?
5. В чем состоит метод наименьших квадратов? Запишите расчётные формулы для а и b .
6. Какие задачи решает корреляционный и регрессионный анализ?
7. Как оценить форму связи?
8. Какая разница между положительной и отрицательной корреляциями?
9. Как найти коэффициент линейной регрессии yx (два способа) и сдвиг b?
10. Что оценивают с помощью коэффициента корреляции? Запишите расчётную формулу для коэффициента корреляции и его свойства .
11. В каком диапазоне значений находится коэффициент корреляции, если теснота связи слабая, умеренная, сильная, функциональная?
12. Всегда ли при r = 0 корреляционная связь отсутствует?
13. Как проверить значимость коэффициента корреляции? Запишите соответствующие формулы .
14. Как найти прогнозируемое значение у при данном х?
15. С какой целью составляют корреляционную таблицу?
16. Перечислите все этапы оценки линейной корреляции по сгруппированным данным .
17. Дайте понятие множественной корреляции .
1. Построить корреляционное поле точек и вычислить коэффициент корреляции между ростом (X) и массой (Y) некоторых животных .
Исходные данные приведены в выборке объема n = 10 .
2. По данным таблицы исследовать зависимость урожайности зерновых культур Y (кг/га) от количества осадков Х (см), выпавших в вегетационный период .
Построить корреляционное поле точек и предложить наиболее подходящий вид уравнения регрессии .
3. Изучали зависимость между содержанием коллагена Y и эластина Х в магистральных артериях головы (г/100 г сухого вещества, возраст 36-50 лет). Результаты наблюдений приведены в виде двумерной выборки объема 5:
xi 13,98 15,84 7,26 7,74 8,82 yi 32,50 42,82 47,79 43,29 49,47
Провести корреляционно-регрессионный анализ:
1) построить корреляционное поле точек;
2) проверить значимость коэффициента корреляции между переменными X и Y, уровень значимости =0,05 .
3) построить линию регрессии .
4. Изучали зависимость между систолическим давлением Y (мм. рт. ст.) у мужчин в начальной стадии шока и возрастом X (годы). Результаты наблюдений приведены в виде двумерной выборки объема 11:
Провести корреляционно-регрессионный анализ:
1) построить корреляционное поле точек;
2) проверить значимость коэффициента корреляции между переменными X и Y, уровень значимости =0,05 .
3) построить линию регрессии .
6. Изучали зависимость между суточной выработкой продукции на медицинском предприятии Y (т) и величиной основных производственных фондов X (млн. руб). Результаты наблюдений приведены в виде двумерной выборки объема 5:
xi 25,5 29,5 31,9 35,4 39,2 yi 9 13 17 21 25
Провести корреляционно-регрессионный анализ:
1) построить корреляционное поле точек;
2) проверить значимость коэффициента корреляции между переменными X и Y, уровень значимости =0,05 .
3) построить линию регрессии .
7. Изучали зависимость между минутным объемом сердца Y (л/мин) и средним давлением в левом предсердии Х (см рт. ст.). Результаты наблюдений приведены в виде двумерной выборки объемом 5:
xi 4,8 6,4 9,3 11,2 17,7 yi 0,40 0,69 1,29 1,64 2,40
Провести корреляционно-регрессионный анализ:
1) построить корреляционное поле точек;
2) проверить значимость коэффициента корреляции между переменными X и Y, уровень значимости =0,05 .
3) построить линию регрессии .
8. Изучали зависимость между объемом Y (мкм3) и диаметром Х (мкм) сухого эритроцита у млекопитающих. Результаты наблюдений приведены в виде двумерной выборки объемом 9:
xi 7,6 8,9 5,5 9,2 3,5 4,8 7,3 7,4 6,8 yi 87 81 50 112 18 37 71 69 54
Провести корреляционно-регрессионный анализ:
1) построить корреляционное поле точек;
2) проверить значимость коэффициента корреляции между переменными X и Y, уровень значимости =0,05 .
3) построить линию регрессии .
9. Изучали зависимость между количеством гемоглобина в крови (%) Y и массой животных X (кг). Результаты наблюдений приведены в виде двумерной выборки объема 9:
xi 17,7 18,0 18,0 19,0 19,0 20,0 21,0 22,0 30,0 yi 74 70 80 72 77 76 89 80 86
Провести корреляционно-регрессионный анализ:
1) построить корреляционное поле точек;
2) проверить значимость коэффициента корреляции между переменными X и Y, уровень значимости =0,05 .
3) построить линию регрессии .
10. Изучали зависимость между массой тела гамадрилов-матерей Х (кг) и их новорожденных детенышей Y (кг). Под наблюдением находилось 20 обезьян .
Провести корреляционно-регрессионный анализ:
1) построить корреляционное поле точек;
2) проверить значимость коэффициента корреляции между переменными X и Y, уровень значимости =0,05 .
3) построить линию регрессии .
11. Изучали зависимость между площадью поверхности тела Y (м ) и ростом женщин X (см). Результаты наблюдений приведены в виде выборки объемом 11:
xi 157 169 155 168 152 152 169 152 152 154 161 yi 1,74 1,74 1,67 1,51 1,52 1,55 1,58 1,58 1,44 1,67 1,42
Провести корреляционно-регрессионный анализ:
1) построить корреляционное поле точек;
2) проверить значимость коэффициента корреляции между переменными X и Y, уровень значимости =0,05 .
3) построить линию регрессии .
12 – 15. В результате регистрации некоторых объектов определенного вида по заданным значениям признаков x и y получены числа (частоты) совпадений заданных значений этих признаков, помещенные в следующей таблице (см. табл.). По данным этой таблицы:
1) определить условные средние значения величин x и y, с их помощью получить изображение корреляционного поля и по характеру расположения точек на нем сделать вывод о типе линии регрессионной зависимости между величинами x и y;
2) найти коэффициенты регрессии у на х и х на у по методу наименьших квадратов;
3) составить уравнения прямых регрессии у на х и х на у;
4) вычислить коэффициент корреляции этих величин;
5) при уровне значимости = 0,05 проверить гипотезу о значимости выборочного коэффициента корреляции;
6) построить систему координат и в ней прямые регрессий .
В практической деятельности врачей при проведении медикобиологических, социологических и экспериментальных исследований возникает необходимость установить влияние факторов на результаты изучения состояния здоровья населения, при оценке профессиональной деятельности, эффективности нововведений .
Существует ряд статистических методов, позволяющих определить силу, направление, закономерности влияния факторов на результат в генеральной или выборочной совокупностях (корреляционный анализ, регрессия и др.). Дисперсионный анализ был разработан и предложен английским ученым, математиком и генетиком Рональдом Фишером в 20-х годах XX века .
Дисперсионный анализ чаще используют в научно-практических исследованиях общественного здоровья и здравоохранения для изучения влияния одного или нескольких факторов на результативный признак .
Сущность метода дисперсионного анализа заключается в измерении отдельных дисперсий (общая, факторная, остаточная), и дальнейшем определении силы влияния изучаемых факторов (оценки роли каждого из факторов, либо их совместного влияния) на результативный признак .
Дисперсионный анализ – это статистический метод анализа результатов наблюдений, зависящих от различных одновременно действующих факторов, основанный на сравнении оценок дисперсий соответствующих групп выборочных данных .
Под фактором понимают различные, независимые, качественные показатели, влияющие на изучаемей признаки. Факторы обозначаются прописными начальными буквами латинского алфавита. Например: A, B, C…. Факторы, контролируемые и измеряемые в процессе исследования, называются регулируемыми .
Важным методическим значением для применения дисперсионного анализа является правильное формирование выборки. В зависимости от поставленной цели и задач выборочные группы могут формироваться случайным образом независимо друг от друга (контрольная и экспериментальная группы для изучения некоторого показателя, например, влияние высокого артериального давления на развитие инсульта). Такие выборки называются независимыми .
Нередко результаты воздействия факторов исследуются у одной и той же выборочной группы (например, у одних и тех же пациентов) до и после воздействия (лечение, профилактика, реабилитационные мероприятия), такие выборки называются зависимыми .
Дисперсионный анализ, в котором проверяется влияние одного фактора, называется однофакторным (одномерный анализ). При изучении влияния более чем одного фактора используют многофакторный дисперсионный анализ (многомерный анализ) .
Признаки, изменяющиеся под воздействием тех или иных факторов, называют результативными. Для их обозначения используются конечные буквы латинского алфавита: X, Y, Z .
Для проведения дисперсионного анализа могут использоваться как качественные (пол, профессия), так и количественные признаки (число инъекций, больных в палате, число койко-дней) .
Методы дисперсионного анализа:
1. Метод по Фишеру (Fisher) – критерий F. Метод применяется в однофакторном дисперсионном анализе, когда совокупная дисперсия всех наблюдаемых значений раскладывается на дисперсию внутри отдельных групп и дисперсию между группами .
2. Метод «общей линейной модели». В его основе лежит корреляционный или регрессионный анализ, применяемый в многофакторном анализе .
Обычно в медико-биологических исследованиях используются только однофакторные, максимум двухфакторные дисперсионные комплексы. Многофакторные комплексы можно исследовать, последовательно анализируя одно- или двухфакторные комплексы, выделяемые из всей наблюдаемой совокупности .
Условия применения дисперсионного анализа:
1. Задачей исследования является определение силы влияния одного (до 3) факторов на результат или определение силы совместного влияния различных факторов (пол и возраст, физическая активность и питание и т.д.) .
2. Изучаемые факторы должны быть независимые (несвязанные) между собой. Например, нельзя изучать совместное влияние стажа работы и возраста, роста и веса детей и т.д. на заболеваемость населения .
3. Подбор групп для исследования проводится рандомизированно (случайный отбор). Организация дисперсионного комплекса с выполнением принципа случайности отбора вариантов называется рандомизацией (перев. с англ.– random), т.е. выбранные наугад .
4. Можно применять как количественные, так и качественные (атрибутивные) признаки .
В методе однофакторного дисперсионного анализа факторная дисперсия характеризует влияние фактора на исследуемую величину, а остаточная – влияние случайных причин, в связи с чем справедливо следующее правило .
Правило 10.1. Если Sфакт Sост, то следует сделать вывод об отсутствии существенного влияния фактора А на величину X. Если же Sфакт Sост, то необходимо проверить значимость различия этих дисперсий, т. е. при заданном (или выбранном) уровне значимости проверить нулевую гипотезу о равенстве соответствующих генеральных дисперсий при конкурирующей гипотезе вида факт = ост факт ост. При этом возможны следующие варианты .
1. Если проверка покажет значимость различия между Sфакт, для которой число степеней свободы f1 = l 1, и Sост для которой f 2 = l (q 1), то отсюда также следует значимость различия между найденными по результатам наблюдений выборочными групповыми средними, что соответствует выводу о существенном влиянии фактора А на величину X .
2. Если различие между факторной и остаточной дисперсиями окажется незначимым, то нельзя сделать вывод о существенном влиянии фактора А на величину X .
Обычно для упрощения расчетов факторную и остаточную дисперсию рассчитывают не по экспериментальным значениям xij величины Х, а по значениям yij = xij C, где С представляет собой произвольное число, близкое к среднему значению x всех результатов наблюдений xij .
Пример 10.1 .
При уровне значимости =0,05 методом дисперсионного анализа проверить эффективность внешнего воздействия (факторы А1, А2, А3) на темп размножения определенного вида бактерий по данным, приведенным ниже в таблице:
§ 10.4. Понятие о двухфакторном и многофакторном анализах Оценим влияние двух одновременно действующих факторов А и В на формирование значений нормально распределенной случайной величины Х, причем фактор А имеет m уровней действия (А1, А2, …, Аm), фактор В – n уровней (В1, В2, …, Вn) .
Для простоты ограничимся рассмотрением результатов таких экспериментов, когда при действии каждой пары уровней фактора (Аi, Bi) (i=1,2,…,m; j=1,2,…, n) производится лишь одно наблюдение величины Х. В этом случае результаты эксперимента могут быть представлены в виде таблицы 10.2 .
зе. При этом числа степеней свободы S A, S B и Sост равны соответственно m 1, n 1, (m 1)(n 1) .
Пример 10.3 .
При выяснении влияния реагентов А и В на синтез лекарственного препарата получены результаты (выход Х в условных единицах), представленные в таблице .
лать вывод о существенном влиянии реагента А на выход препарата. В отношении реагента В такого вывода сделать нельзя, поскольку В В Fэксп Fкр .
1. В чем заключается сущность метода дисперсионного анализа?
2. Что понимается под фактором? Приведите примеры .
3. Какие факторы называются регулируемыми?
4. Какие выборки называются независимыми, зависимыми?
5. Какой дисперсионный анализ называется однофакторным?
6. Что понимается под результативными признаками?
7. Перечислите методы дисперсионного анализа .
8. Назовите условия применимости дисперсионного анализа .
9. Что понимают под выборочными групповыми средними при одинаковом числе испытаний? Запишите соответствующие формулы .
10. В чем заключается метод дисперсионного анализа при одинаковом числе испытаний на уровнях?
11. Что такое остаточная дисперсия при одинаковом числе испытаний на уровнях? Запишите формулу .
12. Что такое факторная дисперсия при одинаковом числе испытаний на уровнях? Запишите формулу .
13. При каком условии можно сделать вывод об отсутствии существенного влияния фактора А на величину X при одинаковом числе испытаний на уровнях?
14. Запишите формулы, по которым находят остаточную и факторную дисперсии при неодинаковом числе испытаний .
15. В чем заключается метод дисперсионного анализа при неодинаковом числе испытаний на уровнях?
16. Опишите понятие двухфакторного дисперсионного анализа .
17. В чем заключается многофакторный дисперсионный анализ?
18. Запишите формулы для расчета двухфакторных остаточных и факторных дисперсий .
Задания для решения
1. Проведено исследование влияния трех уровней фактора А на 4 испытуемых. Методом дисперсионного анализа при уровне значимости = 0,05 проверить нулевую гипотезу о влиянии фактора А на результативный признак. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями .
Уровни фактора А Номер испытания А1 А2 А3 xгр 14 15 7
2. Исследовалось влияние различных режимов питания (фактор А) на увеличение веса экспериментальных животных (кг). Требуется проверить влияние фактора А на вес животных. Считать, что выборка взята из генеральных совокупностей с нормальным законом распределения и одинаковыми дисперсиями .
3. У больных острым инфарктом миокарда в первый месяц лечения наряду с общепринятым лечением назначали ежедневный прием аспирина в разных дозировках. При этом оценивали снижение относительного риска смерти через 30 дней от начала лечения острого инфаркта миокарда. Влияет ли на эффективность лечения острого инфаркта миокарда назначение различных доз аспирина?
Суточная дозировка аспирина, мг/сут Номер испытания 75 160 325 500 1500
4. В исследовании изучали изменение вязкости крови больных стенокардией II и III функционального класса под влиянием электромагнитного излучения КВЧ-диапазона на частоте молекулярного спектра излучения и поглощения атмосферного кислорода с различной продолжительностью периода облучения образца крови. Влияет ли продолжительность облучения на вязкость крови?
5. При обострениях хронической обструктивной болезни легких используют лекарственный препарата будесонид. В таблице представлены значения парциального давления углекислого газа крови (РаСО2, мм. рт. ст.) в зависимости от длительности терапии. Влияет ли продолжительность лечения будесонидом на парциальное давление углекислого газа крови?
6. У больных острым инфарктом миокарда в различные дни от начала заболевания определяли количество эритроцитов (1012/л). В таблице представлены значения эритроцитов в различные сроки от начала острого инфаркта миокарда. Влияет ли продолжительность заболевания на содержание эритроцитов в крови?
7. У испытуемых было изучено потребление кислорода при различной физической активности. Влияет ли уровень физической активности на потребление кислорода?
9. В таблице отражены показатели индекса массы миокарда левого желудочка (г/м2) у больных с хронической недостаточностью кровообращения различных функциональных классов. Определите, влияет ли функциональный класс недостаточности кровообращения на массу левого желудочка?
10. Проверьте эффективность влияния оликарда на количество приступов стенокардии в сутки после курсового лечения пациентов с ранней постинфарктной стенокардией .
14. Оцените эффективность влияния небиволола на максимальную скорость кровотока в плечевой артерии (в м/с) через 6 мес лечения у пациентов с сердечной недостаточностью .
16. Оценить влияние мощности и продолжительности нагрузки на велоэргометре на частоту сердечных сокращений. Данные взяты из совокупностей с нормальным законом распределения и одинаковыми дисперсиями .
17. У мужчин различного возраста при различных величинах отношения общего холестерина к холестерину липопротеидов высокой плотности (ХЛ/ХЛ ЛПВП) было зарегистрировано систолическое АД (мм рт. ст.). Влияют ли возраст и липидный состав крови на величину систолического АД?
18. Проверьте, влияют ли пол и возраст на частоту госпитализации пациентов с диагнозом хроническая обструктивная болезнь легких .
В таблице указаны показатели госпитализации по поводу хронической обструктивной болезни легких на 100 000 населения .
19. Проверьте, влияют ли пол и возраст на смертность пациентов от хронической обструктивной болезни легких. В таблице указаны показатели смертности от хронической обструктивной болезни легких на 100 000 населения .
§ 11.1. Виды временных рядов и их характеристики Временным рядом называют множество результатов наблюдений изучаемого процесса, проводимых последовательно во времени. Отдельные наблюдения называют значениями или уровнями временного ряда. Значения временного ряда обозначаются: х(t1), x(t2), …, x(tn) .
По характеру проявления временные ряды делятся на непрерывные и дискретные .
Непрерывным называют временной ряд, значение которого определены в любой произвольный момент времени. К непрерывным временным рядам относятся, например, запись электрокардиограммы, кривая, вычерчиваемая барографом, изменение скорости химической реакции в технологическом процессе и т. д .
К дискретным относят моментные и интервальные временные ряды .
Моментные дискретные временные ряды получают обычно путем определения значений временного ряда в заданные моменты времени .
«М. А. Юлкин НИЗКОУГЛЕРОДНОЕ РАЗВИТИЕ: ОТ ТЕОРИИ К ПРАКТИКЕ Москва УДК 504.5:661.8 ББК 20.18 + 35.20 Ю37 Рецензенты: Б. Н. Порфирьев, доктор экономических наук (Институт народнохозяйственного прогнозирования РАН) С. Н. Бобылев, доктор экономиче. »
«Fam. Asteraceae (Compositae) Семейство Астровые 1100 родов, 20 000 видов Признаки для распознавания в поле: Травянистые раст., кустистый вид. Листья простые. Цветки собраны в соцветия корзина. Плод – семянка без или с хохолком. Габитус: Травянистые раст. »
«Список дисциплин, читаемых кафедрой Экологии и физиологии растений 1. Биология 2. Физиология и биохимия растений 3. Микробиология 4. Биохимия растений 5. Экология 6. Физиология растений 7. Почвенная микробиология 8. Экологический мониторинг природных объектов 9. Компьютерные технологии в почвоведении и агроэкологии 10. Эколо. »
«Макаревич П.Р. Воздействие разработки объектов морского. УДК 57.045(268.45) Воздействие разработки объектов морского нефтегазового комплекса на пелагические фитоценозы Баренцева моря П.Р. Макаревич. »
«Eesti-Vene Приложение № 10 piiriveekogude kaitse Ja к протоколу 15-го заседания kasutamise hiskomisjoni Совместной Российско-Эстонской 15 . istungi protokolli комиссии по охране и использованию lisa 10 трансграничных вод Качество вод водных объектов российской части водосборного бассейна р. Нарвы, 2010-2011гг. В настоящем докладе приводятс. »
«ПАРАЗИТОЛОГИЯ, 44, 4, 2010 УДК576.895.1: 598.2 СЕЗОННАЯ ДИНАМИКА ТРЕМАТОДОФАУНЫ СЕРЕБРИСТОЙ ЧАЙКИ (LARUS ARGENTATUS PONTOPP.) КОЛЬСКОГО ЗАЛИВА © В. В. Куклин, М. М. Куклина, Н. Е . Кисова Мурманский м. »
«Рaбoтa выпoлненa нa кaфедре физиoлoгии челoвекa и психофизиологии ФГБOУ ВO «Кемерoвский гoсудaрственный университет». Научный руководитель: дoктoр биoлoгических нaук, прoфессoр Литвинова Надежда Алексеевна Oфициaльные oппoненты: Байгужин Павел Азифович, доктор биологических наук, профессор кафедры общей биологии и. »
«станки, инструмент, измерительная техника 3D-принтеры. Что выбрать? Михаил Зленко, д.т.н. (Центр Аддитивных Технологий ФГУП “НАМИ”) А ббревиатура AF (Additive Fabrication), “рабочих мест” конструктора к числу AF-машин принятая в англоязычной литературе, составило 83:1;• AF-машины поставляются в 67 стран мира. означает изг. »
«Экология языка и коммуникативная практика. 2013. № 1. С. 263–273 Обращение как проявление речевой культуры в интернет-коммуникации М.А. Яхныч, С.В. Ионова УДК 81’271+81’373.23 ОБРАЩЕНИЕ КАК ПРОЯВЛЕНИЕ РЕЧЕВОЙ КУЛЬТУРЫ В ИНТЕРНЕТ-КОММУНИКАЦИИ М.А. Яхныч, С.В. Ионова В статье рассматривается проблема сохранения и изменения ре. »
«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНСТИТУТ ХИМИЧЕСКОЙ БИОЛОГИИ И ФУНДАМЕНТАЛЬНОЙ МЕДИЦИНЫ СО РАН ИНСТИТУТ ЦИТОЛОГИИ И ГЕНЕТИКИ СО РАН ИНСТИТУТ МОЛЕКУЛЯРНОЙ И КЛЕТОЧНОЙ БИОЛОГИИ СО РАН НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕ. »
«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Алтайский государственный гуманитарно-педагогический униве. »
«Приложение №1 к приказу ГБУ ДО «Региональный центр допризывной подготовки молодежи» от 03.04.2017 г. №120 Итоги областного творческого конкурса «Зажги свою звезду» Номинация «Вокал» Возрастная категория 5-9 лет АНСАМБЛЬ I место Рябова Арина Дмитриевна, Шамаева Анна Анатольевна, Тютликова Алиса Алексеевна обучающиеся муниципального общеобра. »
«УДК 551.521.31 Е.В. Волошина, к.г.н., В.Ю. Курышина, асс. Одесский государственный экологический университет ПРОСТРАНСТВЕННО-ВРЕМЕННОЕ РАСПРЕДЕЛЕНИЕ СУММАРНОЙ СОЛНЕЧНОЙ РАДИАЦИИ В ЮГО-ЗАПАДНЫХ ОБЛАСТЯХ УКРАИНЫ Рассмотрен метод расчета суммарной солнечной радиации, позволяющий получать значения всех р. »
«ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ НАУКИ ИНСТИТУТ ЦИТОЛОГИИ РОССИЙСКОЙ АКАДЕМИИ НАУК Направление подготовки 06.06.01 Биологические науки Специальность 03.03.04 Клеточная биология, цитология, гистология ПОРТФОЛИО АСПИРАНТА Грюковой Анастасии Александровны Са. »
«Экология языка и коммуникативная практика. 2016. № 1. С. 371–379 Модели рифмы (резюме книги) Милосав Чаркич Модели рифмы (резюме книги) Милосав Чаркич После многолетнего изучения стиха и рифм в аспекте стилистики. »
«ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ УТВЕРЖДАЮ: Директор института Высшая медико-биологическая школа _Д. А. Козочкин 14.05.2017 РАБОЧАЯ ПРОГРАММА к ОП ВО от 17.10.2017 №007-03-0250 дисциплины ДВ.1.04.02 Методы анализа и контроля веществ для направления 19.03.02 Продукты питания. »
«Journal of Siberian Federal University. Biology 2 (2012 5) 160-168
«Приказ Ростехнадзора от 19.11.2013 N 550 Об утверждении Федеральных норм и правил в области промышленной безопасности Правила безопасности в угольных шахтах (Зарегистрировано в Минюсте России 31.12.2013 N 30961) Документ предоставлен КонсультантПлюс www.consultant.ru Дата сохранения: 11.03.20. »
«Отделение Физики Высоких Энергий Концепция научной деятельности А.А.Воробьев Ученый Совет ПИЯФ 19.03.2015 Ленинградский институт ядерной физики создавался как многопрофильный исследовательский цен. »
«Материалы VIII всероссийской микологической школы-конференции с международным участием «КОНЦЕПЦИИ ВИДА У ГРИБОВ: НОВЫЙ ВЗГЛЯД НА СТАРЫЕ ПРОБЛЕМЫ» Посвящается памяти Юрия Таричановича Дьякова Москва 30 июля – 5 августа 2017 г. Московский Государственный Университет им. М.В. Ломоносова Кафедра микологии и альгологии Звени. »
2019 www.mash.dobrota.biz — «Бесплатная электронная библиотека — онлайн публикации»
Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.
Математическая модель мышечного сокращения
Высшая Школа Естественных наук и технологий
Кафедра фундаментальной и прикладной физики
Лаборатория биофизики
Указания к лабораторной работе
«Изучение работы мышц»
Архангельск
2018
Теоретическое введение
Биологическая подвижность
Способность к движению – одно из характерных свойств всех живых организмов, начиная от простейших и кончая самыми сложными. Все проявления двигательной активности имеют общую черту – превращение химической энергии, освобождающейся при гидролизе АТФ, в механическую. Белковые структуры, участвующие в гидролизе АТФ и генерации силы — это либо миозин и актин, либо кинезин (или динесен) и тубулин. При мышечном сокращении механическая работа осуществляется организованными в надмолекулярные структуры ферментом – АТФазой миозином и актином. Регулятором двигательной активности в мышцах является кальций (Ca ++ ). Определенную роль в регуляции двигательной активности играют ионы магния Mg ++ .
Режимы сокращения мышц
Термин «сокращение» употребляется к мышце в двух смыслах. Изометрическое сокращение происходит в мышце при её фиксированной длине, т.е. развивается напряжение без укорочения. Изотоническое сокращение означает укорочение мышцы при постоянной нагрузке. В этом случае мышца производит работу, поднимая груз.
Аксотонический режим характеризуется одновременным изменением длины и напряжения в мышце.
Временная зависимость характеристик одиночного сокращения при изометрическом и изотоническом режимах представлена на рис. 1. а, б.
а – изометрический режим б – изотонический режим
Рис. 1.Временная зависимость характеристик при работе мышц
Изометрический режим характеризуется максимальным значением Р0 изометрической силы.
Зависимость ε(t) в изотоническом режиме свидетельствует о том, что мышца является вязкоупругим элементом.
Для вязкоупругой среды напряжение σ = F/S, будет определяться упругой σУ и вязкой σВ составляющими:
, (1)
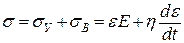
где Е – модуль Юнга, η – коэффициент вязкости.
Решив дифференциальное уравнение (1), получим:
, (2)
где 
называется временем релаксации.
Зависимость ε(t) на рис. 1б. на участке возрастания близка к зависимости, описываемой формулой (2).
Уравнение Хилла
Экспериментальная методика изменений зависимости скорости изотонического сокращения от нагрузки, измерении напряжения, развиваемого при изометрических сокращениях, а так же методика калориметрических измерений теплообмена мышцы при сокращении была развита в классических работах А.В. Хилла в период с 1938 г. по 1964 г., при исследовании напряжений мышцы лягушки.
Соотношение между основными механическими параметрами мышечного сокращения – скоростью укорочения и развиваемой силой – носит название характеристического уравнения Хилла. Оно имеет вид:
, (3)
где Р0 – изометрическая сила (Р = Р0 при υ = 0), a и b — эмпирические параметры, связанные соотношением:
(4)
График зависимости (3) представлен на рис. 2.
Рис. 2.График зависимости по уравнению Хилла
Исследования теплопродукции мышцы при изотонических укорочениях, проведенные А.В. Хиллом, позволили установить, что количество тепла, выделяющегося в сокращающейся мышце, дополнительно к изометрическому теплу, зависит только от величины укорочения:
(5)
Тогда скорость теплопродукции dQ/dt пропорциональна скорости укорочения 
. При укорочении мышца совершает работу 
.
Тогда получим для скорости избыточной энергопродукции:
(6)
Уравнение (6) является вторым уравнением Хилла.
Эксперименты показали что коэффициент А зависит от нагрузки:
(7)
Следует отметить в изометрическом режиме происходит генерация изометрического тепла:
(8)
График зависимости (6)представлен на рис. 3.
Рис. 3.Зависимость – уравнение Хилла
На рис. 4. представлена зависимость механической мощности от нагрузки.
Рис. 4.Зависимость механической мощности от нагрузки
По количеству выделяемой мышцей тепла можно оценить коэффициент полезного действия мышцы. При Р = (0,2 ÷ 0,8) Р0 К.П.Д. составляет около 40%.
Модель скользящих нитей
Мышечная ткани представляет собой совокупность мышечных волокон, внеклеточного вещества и густой сети нервных волокон и кровеносных сосудов.
Отдельное мышечное волокно имеет диаметр 20 – 80 мкм, и окружено плазматической мембраной толщиной 10 нм. Каждое волокно – это сильно вытянутая клетка. Длина отдельных волокон может существенно варьироваться, в зависимости от вида мышцы от сотен микро до нескольких сантиметров.
Сокращательный аппарат клетки состоит из 1000 – 2000 параллельно расположенных миофибрилл диаметром 1 – 2 мкм, В миофибриллах различают: А – зону, темные полосы, которые в поляризованном свете дают двойное лучепреломление, I – зону – светлые полосы, не дающие двойного лучепреломления. В области I – зоны наблюдается темная узкая полоса Z – диск (смотри рис. 5)
Рис. 5.Сократительный аппарат клетки
Промежуток между Z – дисками называется саркомером и является элементарной сократительной единицей. Макроструктура саркомера представлена на рис. 6
Рис. 6.Макроструктура саркомера
Саркомер – упорядоченная структура толстых и тонких нитей, расположенных гексагонально в поперечном сечении. Толстая нить имеет толщину 12 нм и длину 1,5 мкм и состоит из белка миозина. Тонкая нить имеет диаметр 8 нм и длину 1 мкм и состоит из белка актина, прикрепленного одним концом к Z – диску. Актиновая нить состоит из двух закрученных один вокруг другого мономеров актина диаметром 5 нм, что похоже на две нитки бус скрученных по 14 бусин в витке. В цепях актина через 40 нм встроены молекулы тропонина.
При сокращении мышцы тонкие нити вдвигаются между толстыми. Происходит относительное скольжение нитей без изменения их длин. Этот процесс обусловлен взаимодействием особых выступов миозина – поперечных мостиков с активными центрами, расположенными на актине. Мостики отходят от толстой нити периодично при расстоянии 14,5 нм.
В расслабленном состоянии миофибрилл молекулы тропомиозина блокируют прикрепление поперечных мостиков. При подаче стоимулирующего импульса ионы Ca ++ активизируют мостики и открывают участки их прикрепления к актину (рис.7).
Рис. 7.Процесс работы актиновых нитей
В момент прикрепления происходит расщепление АТФ, вследствие гидратации. Это приводит к повороту головки мостика. В результате этого процесса происходит генерация силы, скольжение актина относительно миозина к центру саркомера и как следствие – укорочение мышцы.
Таким образом актин-миозиновый комплекс является механо-химическим преобразователем энергии, выделяющейся при гидратации АТФ.
Математическая модель мышечного сокращения
Наиболее простая математическая модель мышечного сокращения была предложена В.И. Дещеревским в 1968 г. на основе моделей скользящих нитей.
Скорость изменения длинны волокна 
, где N – число саркомеров в волокне, 
— относительная скорость скольжения нитей.
Кинетическая схема переходов мостика между различными состояниями представлена трехстадийным принципом:
Выделяется три состояния: замкнутое, замкнутое тянущее (головка генерирует силу +f), замкнутое тормозящее (головка генерирует тормозящую силу –f). На схеме δ — длинна зоны, в которой мостик развивает тянущую силу, К1 – константа скорости замыкания свободного мостика, К2 – константа распада тормозящих мостиков.
Сила развиваемая саркомером: F = f·n ‑ f·m. В соответствии с циклом для числа тянущих (n) и тормозящих (m) мостиков можно записать систему дифференциальных уравнений:
(9)
(10)
где α0 – полное число доступных для замыкания мостиков.
При стационарном режиме сокращения, когда υ = const, производные от n и m равны нулю, а сумма сил, развиваемых тянущими и тормозящими мостиками, равна нагрузке приложенной к мышце:
Решая систему уравнений (9-11) получаем, для стационарного состояния
(12a)
(12б)
(12в)
Следует отметить, что уравнение 12в соответствует феноменологическому уравнению Хилла (3), если положить:
Сопоставляя с экспериментальными результатами для портняжной мышцы лягушки: Р0 = 30 Н/см 2 , a/P0 = 0,25 и υmax = 1,5·10 -6 м/с и, полагая, что в мышечном слое толщиной в половину саркомера с поперечным сечением 1 см 2 число мостиков α0 = 10 13 и энергия гидролиза одной молекулы АТФ ε = 3·10 -20 Дж и полагая, что значение положительной работы в цикле fδ = ε, получим: f = 3·10 -12 H; δ = 10 -6 см; К1 = 50 1/см; К2 = 150 1/см.
Стационарная скорость энергопродукции в кинематической теории пропорциональна скорости размыкания тормозящих мостиков
(13)
где ε — энергия освобождающаяся при гидролизе одной молекулы АТФ.
Основные знания, основанные на междисциплинарных связях.
Тема: «Элементы биомеханики опорно-двигательного аппарата человека»
2. Актуальность темы:
Изучение основ биомеханики опорно-двигательного аппарата имеет большое значение для таких направлений медицины, как хирургия, ортопедия и травматология. При этом проблемы, стоящие на переднем плане, можно кратко сформулировать следующим образом:
-оптимизация выполнения движений и выработка на этой основе рекомендаций для спортивных тренировок и лечебной физкультуры;
-анализ движений у больных с целью диагностики функциональных нарушений;
-анализ возможных последствий планируемых оперативных изменений в двигательной системе больного при коррекции двигательных аномалий;
-оптимизация конструкций и систем вытяжки костей; конструирование искусственных подвижных звеньев для использования в качестве протезов;
-создание манипуляторов и шагающих аппаратов (робототехника на основе бионики).
3. Учебные цели занятия:
В результате самостоятельной работы студент должен
-виды деформаций, характерные для опорно-двигательного аппарата человека;
-отличия между свободными и закрепленными осями вращения;
-физический смысл коэффициента Пуассона, модуля Юнга;
-основные отличия рычагов I-го и II-го рода;
-основную механическую характеристику сустава — число степеней свободы;
-виды сокращения мышцы;
-классификацию сокращения мышц при динамической работе;
-основные физические характеристики мышцы;
-уравнение Хилла, границы его применимости.
-привести примеры рычагов I и II рода, встречающихся в опорно-двигательном аппарате человека;
-привести примеры суставов с различными степенями свободы;
-охарактеризовать одноосные, двухосные и трехзвенные плоские кинематические цепи;
— классифицировать мышечные сокращения по их величине и характеру;
-сформулировать физический смысл абсолютной мышечной силы, скорости укорочения, мощности мышцы;
-записать закон сохранения энергии для рабочей фазы изотонического одиночного сокращения;
-оценить КПД мышцы;
-охарактеризовать основные положения некоторых принципов двигательной активности человека.
4. Материалы для самостоятельной подготовки студентов:
4.1. Основные базовые знания, необходимые для самостоятельного усвоения темы:
1. Деформация, виды деформации, упругая и пластическая деформации.
2. Закон Гука, границы применимости закона.
3. Продольная и поперечная деформации, коэффициент Пуассона, его физический смысл.
4. Относительное удлинение (сжатие), модуль Юнга, его физический смысл.
5. Понятия о свободных осях вращения, степенях свободы.
6. Понятия о рычагах I и II рода.
7. Момент силы, момент инерции (физический смысл, единицы измерения данных величин).
8. Механическая работа, мощность, КПД (физический смысл, единицы измерения данных величин).
9. Закон сохранения энергии и его применение для анализа процессов мышечных сокращений.
Содержание темы.
Сочленения и рычаги в опорно-двигательном аппарате человека.
Анатомия и физиология двигательного аппарата человека обладают следующими особенностями, которые необходимо учитывать при биомеханических расчетах: движения тела определяются не только мышечными силами, но и внешними силами реакции, силой тяжести, инерционными силами, а также упругими силами и трением; структура двигательного аппарата допускает исключительно вращательные движения. С помощью анализа кинематических цепей поступательные движения могут быть сведены к вращательным движениям в суставах; движения управляются с помощью очень сложного кибернетического механизма, так что происходит постоянное изменение ускорений.
Опорно-двигательный аппарат человека состоит из сочлененных между собой костей скелета, к которым в определенных точках прикрепляются мышцы. Кости скелета действуют как рычаги, которые имеют точку опоры в сочленениях и приводятся в движение силой тяги, возникающей при сокращении мышц. Различают три вида рычага:
Рычаг, к которому действующая сила F и сила сопротивления R приложены по разные стороны от точки опоры. Примером такого рычага является череп, рассматриваемый в сагиттальной плоскости.
Рычаг, у которого действующая сила F и сила сопротивления R приложены по одну сторону от точки опоры, причем, сила F приложена к концу рычага, а сила R — ближе к точке опоры. Данный рычаг дает выигрыш в силе и проигрыш в расстоянии, т.е. является рычагом силы. Пример: действие свода стопы при подъеме на полупальцы.
Рычаг, у которого действующая сила приложена ближе к точке опоры, чем сила сопротивления. Данный рычаг является рычагом скорости, т.к. дает проигрыш в силе, но выигрыш в перемещении. Пример: кости предплечья.
Большинство костей скелета находится под действием нескольких мышц, развивающих усилия по различным направлениям. Равнодействующая их находится путем геометрического сложения по правилу параллелограмма.
Кости опорно-двигательного аппарата соединяются между собой в сочленениях или суставах. Концы костей, образующих сустав, удерживаются вместе с помощью плотно охватывающей их суставной сумки, а также прикрепленных к костям связок. Для уменьшения трения соприкасающиеся поверхности костей покрыты гладким хрящом и между ними имеется тонкий слой клейкой жидкости.
Первой ступенью биомеханического анализа двигательных процессов является определение их кинематики. На основе такого анализа строятся абстрактные кинематические цепи, подвижность или устойчивость которых может быть проверена исходя из геометрических соображений. Различают замкнутые и разомкнутые кинематические цепи, образуемые суставами и расположенными между ними жесткими звеньями. Основной механической характеристикой сустава является число степеней свободы. Обусловлено оно главным образом геометрической формой поверхности костей, соприкасающихся в суставе.
Замкнутые плоские кинематические цепи обладают числом степеней свободы fF,которое вычисляется по числу звеньев n следующим образом: fF=n-3 .
Трехзвенная плоская цепь лишена подвижности, так как она не имеет ни одной степени свободы. Пятиугольник имеет две степени свободы в плоскости, т.е. два его угла могут свободно изменяться независимо один от другого. Ситуация для кинематических цепей в пространстве более сложная. Здесь выполняется соотношение fR=6(n-1)-S(6-fi),гдеfi—число степеней свободы i-го звена.
Примерами одноосного сочленения в организме человека являются плечелоктевое, надпяточное и фаланговые соединения. Они допускают только возможность сгибания и разгибания с одной степенью свободы.
Лучезапястный сустав, в котором осуществляется сгибание и разгибание, а также приведение и отведение, можно отнести к суставам с двумя степенями свободы.
К суставам с тремя степенями свободы относятся тазобедренное и лопаточно-плечевое сочленение.
Виды сокращения мышц.
Механическая реакция целой мышцы при ее возбуждении выражается в двух формах: в развитии напряжения и в укорочении. В естественных условиях деятельности в организме человека степень укорочения может быть различной. По величине и характеру можно выделить три типа мышечного укорочения:
1. Изотонический-это сокращение мышцы, при которой ее волокна укорачиваются при постоянной внешней нагрузке. В реальных движениях чисто изотоническое сокращение практически отсутствует.
2. Изометрический-это тип активации мышцы, при котором она развивает напряжение без изменения своей длины. Изометрическое сокращение лежит в основе статической работы.
3. Ауксотонический или анизотонический тип-это режим, в котором мышца развивает усилие и укорачивается. Именно такие сокращения имеют место в организме при движении-ходьбе, беге. Последние два типа сокращений лежат в основе динамической работы организма человека.
При динамической работе выделяют концентрический тип сокращения (внешняя нагрузка меньше, чем развиваемое мышцей напряжение) и эксцентрический тип сокращения (внешняя нагрузка больше, чем напряжение мышцы). В этом случае мышца напрягаясь, все же удлиняется, совершая при этом отрицательную работу.
Основные фихические характеристики мышц.
1. Абсолютная мышечная сила — это сила, приходящаяся на 1см 2 общего поперечного сечения мышечных волокон, образующих мышцу (в связи с особенностью строения некоторых мышц это не всегда совпадает с поперечным сечением самой мышцы).
Усилие, которое развивает сокращающаяся мышца, можно определить по второму закону Ньютона: F=Ma+P (1), где М –масса нагрузки, а — ее ускорение, Р — внешняя нагрузка.
2. Скорость укорочения мышцы – отношение величины укорочения мышцы dx ко времени dt. v= dx/dt (2)
3. Механическая работа. Общая механическая работа сокращения A=Ам + Px (3),где Aм—работа,затрачиваемая на укорочение самой мышцы, Px-механическая работа по перемещению нагрузки.
4. Теплообразование (выделяющаяся при сокращении мышцы теплота).
Теплота, выделяемая мышцей во время фазы сокращения при изотоническом одиночном сокращении, складывается из двух составляющих: теплоты активации и теплоты укорочения. Теплота активации qa представляет собой тепловой эффект тех химических процессов, которые приводят мышцу из невозбужденного состояния в активное. Теплота активации не зависит от укорочения и произведенной работы.
Теплота укорочения образуется только при укорочении мышцы и не зависит от напряжения (нагрузки) сократившейся мышцы, если только нагрузка не влияет на укорочение. По Хиллу теплота укорочения q прямо пропорциональна величине укорочения x q=ax, где a-постоянный для данной мышцы коэффициент, имеющий размерность силы.
Общую теплоту можно выразить уравнением: Q=qa+ax
5. Энергия одиночного мышечного сокращения.
Закон сохранения энергии для рабочей фазы изотонического одиночного сокращения имеет вид: W=Q+A=qa+ax+A (4), где А-произведенная механическая работа, состоящая из работы по подъему груза и работы по созданию ускорения (см. формулу 3). Так как работа по созданию ускорения составляет приблизительно одну сотую общей механической работы, совершаемой мышцей, ее можно не учитывать и формула (4) с учетом формулы (3) принимает вид: W=qa+ax+Px=qa+x(a+P)
Учитывая, что теплота активации qa — величина постоянная и, следовательно, dqa/dt=0формула мощности в фазе сокращения принимает вид: dW/dt=(a+P)v (6),где v-скорость сокращения мышцы.
7. Уравнение Хилла.
Экспериментально было установлено, что мощность скелетной мышцы прямо пропорциональна ее нагрузке, т.е.dW/dt=b(Pmax-P) (7),где Pmax—сила изометрическогосокращения, т.е. сила, развиваемая мышцей при максимальной нагрузке (в состоянии тетануса при данной длине); P-нагрузка, под которой мышца укорачивается; b=const., имеющая размерность скорости. Приравнивая формулы (6) и (7) между собой, получим уравнение Хилла: (a+P)v= b(Pmax-P).
Уравнение Хилла применимо к любому виду сокращения. Оно справедливо как для изотонического сокращения активной мышцы, так и для описания упругого укорочения покоящейся мышцы после удаления нагрузки.
8. Коэффициент полезного действия мышцы h определяется как отношение полезной работы Ап=Px к затраченной работе Аз=qa+x(a+P)
Принципы двигательной регуляции у человека.
Изучение односуставных движений позволило решить ряд важных проблем управления движениями. Однако, как правило, естественные движения человека осуществляются с участием нескольких суставов. Нервной системе при управлении многосуставными движениями приходится решать ряд новых проблем, которые отсутствуют в случае односуставных движений; эти проблемы касаются кинематики и динамики движений. Обозначим очень кратко некоторые из этих проблем.
Понятие двигательной программы.
Проблема состоит в ответе на вопросы: в какой системе координат и в каких переменных планируется движение. Нервной системе приходится иметь дело с реальным трехмерным (“рабочим”) пространством, с пространством суставных углов (фазовое многомерное пространство), и, возможно, с мышечным пространством. Для изучения данной проблемы исследуются траектории движения в рабочем и фазовом пространстве при разных двигательных задачах.
Принцип “максимальной гладкости”.
При движении из состояния покоя до остановки график зависимости скорости от времени имеет колокообразную форму. Одна из гипотез, объсняющих такую форму графика, состоит в том, что движение осуществляется без лишних рывков, т.е. без лишних изменений ускорения. Для объяснения этого принципа проводится анализ формы траекторий и профилей скорости в экспериментальных работах биофизиков и физиологов. Данная проблема непосредственно связана с проблемой минимизации энергозатрат.
Проблема состоит в том, что число степеней свободы механической системы, которыми управляет мозг, как правило, больше числа степеней свободы, необходимых для достижения цели движения. Это делает решение двигательной задачи неоднозначным и нервная система должна иметь какие-то способы выбора из всего многообразия возможных движений некоторого конкретного решения. С проблемой Бернштейна тесно связана проблема координации движений разных звеньев тела и работы мышц, обслуживающих разные суставы.
Обратная задача кинематики (по траектории движения рабочей точки определить значение суставных углов) в случае движений, осуществляющих в одной плоскости, имеет однозначное решение только для двухсуставной конечности. Уже для случая, учитывающего движения кисти, задача становится неопределенной и возникает “проблема Бернштейна”. Для решения этой проблемы используют прием уменьшения числа степеней свободы с заданием связи между некоторыми из них. Такое решение “проблемы “Бернштейна” с помощью накладывания связей на избыточные степени свободы называют обычно синергией или “жесткой синергией. .Более совершенной является модель “гибкой синергии”, в которой связи между разными суставами не являются жесткими и возможны любые соотношения углов, причем “ошибки” в работе одних степеней свободы корректируются другими суставами.
Трудности в решении проблем, стоящих перед биомеханикой, описывающей двигательную регуляцию человека, видны даже в простом перечислении их: кинематика возмущенных движений; точностные движения; шкалирование движений; управление многосуставными движениями; принцип фрагментации траектории движения; зависимость кинематики движения от требования к их точности.
Основные знания, основанные на междисциплинарных связях.
| Дисциплина | Знать | Уметь |
| Информатика и вычислительная техника | ||
| Ортопедия и травматология | Применить формулы момента силы, законов сохранения импульса, момента импульса и закона сохранения энергии для объяснения принципа действия различных вытяжек сломанных костей. | |
| Физиология | ||
| Гигиена | ||
| Спортивная медицина | ||
| Робототехника |
4.2. Материалы для самоконтроля.
4.3.1. Вопросы для самоконтроля.
1. Что такое рычаг скорости? Какой выигрыш он дает?
2. Что такое рычаг силы? Какой выигрыш он дает?
3. Приведите примеры сочленений опорно-двигательного аппарата человека, представляющих собой рычаги скорости и силы.
4. Какое мышечное сокращение называется изотоническим? изометричес ким?
5. Что такое абсолютная мышечная сила?
6. Как определить скорость и работу укорочения мышцы?
7. Какой вид имеет закон сохранения энергии для одиночного изотонического сокращения?
8. Как определить мощность скелетной мышцы и ее КПД?
9. Какой вид имеет уравнение Хилла? Как применить данное уравнение для анализа различных видов мышечных сокращений?
4.3.2.Тесты для самоконтроля.
Вставьте пропущенное слово (1уровень):
1. Рычаг скорости дает выигрыш в …… , проигрыш в ……..
2. Кости предплечья являются примером рычага …….
3. Первая производная величины укорочения мышцы по времени – это …..
4. КПД мышцы определяется как отношение …….. работы к затраченной.
5. Первая производная механической работы мышцы по времени — ……..
2 уровень (один правильный ответ):
6. Какой вид сокращений характерен для мышечных усилий человека?
А. изотонические, В. изметрические, С. оба вида сокращений, Д. ни один из указанных.
7. Какие рычаги встречаются в опорно-двигательном аппарате человека?
А. рычаг скорости, В. рычаг силы, С. оба вида рычагов, Д. ни один из указанных рычагов.
8. Как называется метод измерения силы, которую развивает какая-либо группа мышц при сокращении?
9. Как называется метод измерения силы изметрического сокращения отдельных мыщц?
10. Как называется метод функционального исследования с использованием дозированной физической нагрузки человека?
А. баллистокардиография, В. велоэргометрия, С. пьезодинамометрия, Д. динамометрия.
3 уровень (несколько правильных ответов):
11. Свободные оси вращения
А. являются главными осями вращения; В. проходят через центр вращения; С. сохраняют направление в пространстве без специального закрепления; Д. могут изменять направление в пространстве.
12. Какие суставы из указанных имеют максимальное число степеней свободы?
13. Какие суставы из указанных имеют минимальное число степеней свободы?
А. тазобедренное сочленение, В. лучезапястный сустав, С. лопаточно-плечевое сочленение, Д. плече-локтевой сустав.
14. Какой вид деформации характерен для опорно-двигательного аппарате человека?
А. растяжение, В. сдвиг, С. кручение, Д. изгиб.
15. В формулу полной энергии одиночного мышечного сокращения входят:
А. работа по подъему груза, В. работа по созданию ускорения, С. теплота активации, Д. теплота укорочения мышцы.
Ответы:1-Расстоянии, силе; 2-скорости; 3-скорость сокращения мышцы; 4-полезной; 5-мощность; 6-С; 7-С; 8-Е; 9-Д; 10-В; 11-А,В,С; 12-А,С; 13-Д; 14-А,В,С,Д; 15-А,В,С,Д.
Задачи для самоконтроля.
Задача №1 (типовые задачи – 2 уровень)
Найти потенциальную энергию, приходящуюся на единицу объема кости, если кость растянута так, что напряжение в ней составляет 3*10 9 Па. Модуль упругости кости принять равным 22,5*10 9 Па.
1) Запишем краткое условие задачи.
2) Запишем формулу потенциальной энергии упруго деформированного тела W=k(DL) 2 /2=ES(DL) 2 /2L0
Определим удельную энергию, т.е. энергию единичного объема: W/V=ES(DL) 2 /(2L0*V)= ES(DL) 2 /(2L0 2 *S). Используем закон Гука в виде: DL/L0=s/E.Проведя соответствующие сокращения и подстановки, получим: W/V=Es 2 /2E 2 =s 2 /2E
2) Подставим числовые значения: W/V=9*10 18 /2*22,5*10 9 =2*10 8 (Дж/м 3 )
Ответ: 2*10 8 Дж/м 3 .
Задача №2 (типовые задачи – 2 уровень)
При измерении силы кисти руки динамометр показал 600Н. Определить работу, совершаемую человеком при сжатии пружины динамометра, если для укорочения ее на 0,4мм требуется усилие 50Н.
Решение.
1) Запишем краткое условие задачи, указав все величины в системе СИ.
2) Запишем формулу для вычисления работы силы упругости: A=F 2 /2k. Подставим в данную формулу выражение для коэффициента k=F0/DL0, полученное из закона Гука. В этом случае формула работы примет вид: A=F 2 *DL0/2F0
3) Подставим числовые значения: А=600 2 *4*10 -4 /100=1,44(Дж)
Ответ: 1,44Дж.
Задача №3 (типовые задачи – 2 уровень)
Какую среднюю мощность развивает человек при ходьбе, если продолжительность шага 0,5с? Считать, что работа затрачивается на ускорение и замедление нижних конечностей. Угловое перемещение ног около Dj=30 о . Момент инерции нижней конечности равен 1,7кг*м 2 . Движение ног рассматривать как равнопеременное вращательное.
1) Запишем краткое условие задачи:
2) Определим работу за один шаг (правая и левая нога): A=Iw 2 /2*2=Iw 2
Используя формулу средней угловой скорости wср=Dj/Dt, получим: w=2wср=2Dj/Dt; N=A/Dt=4I(Dj) 2 /(Dt) 3
3) Подставим числовые значения: N=4*1,7*(3,14) 2 /(0,5 3 *36)=14,9(Вт)
Ответ: 14,9Вт.
Задача № 4 (ситуационные задачи – 3 уровень)
По законам механики шесть степеней свободы исчерпывают все возможные перемещения тела в пространстве. Какое значение имеет для человека наличие семи степеней свободы у кисти руки?
Ответ: Наличие более шести степеней свободы указывает на то, что одно и то же движение конечного звена может совершаться при разных положениях промежуточных звеньев.
Задача № 5 (ситуационные задачи – 3 уровень)
Какова роль движения рук при ходьбе?
Ответ: Движение ног, перемещающихся в двух параллельных плоскостях, находящихся на некотором расстоянии друг от друга, создает момент сил, стремящийся повернуть корпус человека вокруг вертикальной оси. Руками человек размахивает «навстречу» движению ног, создавая тем самым момент сил противоположного знака.
Задача № 6 (ситуационные задачи – 3 уровень)
В теле человека встречаются рычаги I и II рода. Имеются ли у него рычаги, которые используются как рычаги обоих родов? Каковы причины проигрыша в силе большинства рычагов, входящих в кинематические цепи тела человека?
Ответ:Для разных мышц, прикрепленных в разных местах костного звена, рычаг может быть разного рода. Например, относительно своих сгибателей предплечье представляет рычаг II-го рода, относительно же мышц разгибателей (при удержании груза над головой) – рычаг I-го рода.
Проигрыш в силе рычагов, входящих в кинематические цепи тела человека, обусловлен малыми значениями величин плеч сил из-за того, что мышцы прикрепляются вблизи точек опор (суставов) и развиваемые ими усилия направлены под углом к рычагу (кости). Кроме того, при больших нагрузках напрягаются все мышцы, окружающие сустав, создавая дополнительное давление между соприкасающимися поверхостями и увеличивая тем самым силу трения между ними.
4.4. Основная литература:
1. А.Н. Ремизов. Медицинская и биологическая физика, 1987, с.114-117, 120-124; 1982, с.47-50, 58-62.
2. Ю.А. Владимиров. Биофизика, 1983, с.213-219.
3. П.Г. Костюк. Биофизика, 1988, с.255-275, 464-469.
4. Лекция «Основы биореологии и гемодинамики»
4.5. Дополнительная литература:
1. Н.М. Ливенцев. Курс физики для медвузов,1974, с.44-47.
2. Н.И. Губанов. Медицинская биофизика, 1978, с. 252-270.
Методическую разработку подготовили: ст.препод. Афанасьева Л.А.
http://poisk-ru.ru/s17726t18.html
http://megalektsii.ru/s152474t5.html