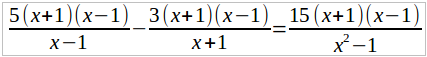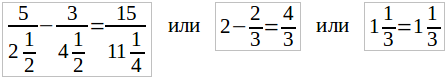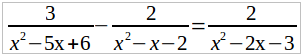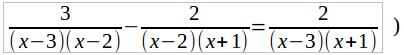Сложное уравнение по алгебре с ответами

Математика

52. Более сложные примеры уравнений.
Пример 1 .

5/(x – 1) – 3/(x + 1) = 15/(x 2 – 1)

Общий знаменатель есть x 2 – 1, так как x 2 – 1 = (x + 1)(x – 1). Умножим обе части этого уравнения на x 2 – 1. Получим:

или, после сокращения,

5(x + 1) – 3(x – 1) = 15

5x + 5 – 3x + 3 = 15

Рассмотрим еще уравнение:

5/(x-1) – 3/(x+1) = 4(x 2 – 1)

Решая, как выше, получим:

5(x + 1) – 3(x – 1) = 4
5x + 5 – 3x – 3 = 4 или 2x = 2 и x = 1.

Посмотрим, оправдываются ли наши равенства, если заменить в каждом из рассмотренных уравнений x найденным числом.

Для первого примера получим:

Видим, что здесь нет места никаким сомнениям: мы нашли такое число для x, что требуемое равенство оправдалось.

Для второго примера получим:

5/(1-1) – 3/2 = 15/(1-1) или 5/0 – 3/2 = 15/0

Здесь возникают сомнения: мы встречаемся здесь с делением на нуль, которое невозможно. Если в будущем нам удастся придать определенный, хотя бы и косвенный, смысл этому делению, то тогда мы можем согласиться с тем, что найденное решение x – 1 удовлетворяет нашему уравнению. До этой же поры мы должны признать, что наше уравнение вовсе не имеет решения, имеющего прямой смысл.

Подобные случаи могут иметь место тогда, когда неизвестное входит как-либо в знаменатели дробей, имеющихся в уравнении, причем некоторые из этих знаменателей, при найденном решении, обращаются в нуль.

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

Можно сразу видеть, что данное уравнение имеет форму пропорции: отношение числа x + 3 к числу x – 1 равно отношению числа 2x + 3 к числу 2x – 2. Пусть кто-либо, в виду такого обстоятельства, решит применить сюда для освобождения уравнения от дробей основное свойство пропорции (произведение крайних членов равно произведению средних). Тогда он получит:

(x + 3) (2x – 2) = (2x + 3) (x – 1)

2x 2 + 6x – 2x – 6 = 2x 2 + 3x – 2x – 3.

Здесь может возбудить опасения, что мы не справимся с этим уравнением, то обстоятельство, что в уравнение входят члены с x 2 . Однако, мы можем от обеих частей уравнения вычесть по 2x 2 — от этого уравнение не нарушится; тогда члены с x 2 уничтожатся, и мы получим:

6x – 2x – 6 = 3x – 2x – 3

Перенесем неизвестные члены влево, известные вправо — получим:

Вспоминая данное уравнение

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

мы сейчас же подметим, что найденное значение для x (x = 1) обращает в нуль знаменателей каждой дроби; от такого решения мы, пока не рассмотрели вопроса о делении на нуль, должны отказаться.

Если мы подметим еще, что применение свойства пропорции усложнило дело и что можно было бы получить более простое уравнение, умножая обе части данного на общий знаменатель, а именно на 2(x – 1) — ведь 2x – 2 = 2 (x – 1), то получим:

2(x + 3) = 2x – 3 или 2x + 6 = 2x – 3 или 6 = –3,

Это обстоятельство указывает, что данное уравнение не имеет таких, имеющих прямой смысл решений, которые не обращали бы знаменателей данного уравнения в нуль.
Решим теперь уравнение:

(3x + 5)/(x – 1) = (2x + 18)/(2x – 2)

Умножим обе части уравнения 2(x – 1), т. е. на общий знаменатель, получим:

Найденное решение не обращает в нуль знаменатель и имеет прямой смысл:

или 11 = 11

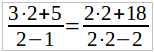
Если бы кто-либо, вместо умножения обеих частей на 2(x – 1), воспользовался бы свойством пропорции, то получил бы:

(3x + 5)(2x – 2) = (2x + 18)(x – 1) или
6x 2 + 4x – 10 = 2x 2 + 16x – 18.

Здесь уже члены с x 2 не уничтожались бы. Перенеся все неизвестные члены в левую часть, а известные в правую, получили бы

Это уравнение мы теперь решить не сумеем. В дальнейшем мы научимся решать такие уравнения и найдем для него два решения: 1) можно взять x = 2 и 2) можно взять x = 1. Легко проверить оба решения:

1) 2 2 – 3 · 2 = –2 и 2) 1 2 – 3 · 1 = –2

Если мы вспомним начальное уравнение

(3x + 5) / (x – 1) = (2x + 18) / (2x – 2),

то увидим, что теперь мы получим оба его решения: 1) x = 2 есть то решение, которое имеет прямой смысл и не обращает знаменателя в нуль, 2) x = 1 есть то решение, которое обращает знаменателя в нуль и не имеет прямого смысла.

Найдем общего знаменателя дробей, входящих в это уравнение, для чего разложим на множители каждого из знаменателей:

1) x 2 – 5x + 6 = x 2 – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),

2) x 2 – x – 2 = x 2 – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),

3) x 2 – 2x – 3 = x 2 – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).

Общий знаменатель равен (x – 3)(x – 2)(x + 1).

Умножим обе части данного уравнения (а его мы теперь можем переписать в виде:

на общего знаменателя (x – 3) (x – 2) (x + 1). Тогда, после сокращения каждой дроби получим:

3(x + 1) – 2(x – 3) = 2(x – 2) или
3x + 3 – 2x + 6 = 2x – 4.

Это решение имеет прямой смысл: оно не обращает в нуль ни одного из знаменателей.

Если бы мы взяли уравнение:

то, поступая совершенно так же, как выше, получили бы

3(x + 1) – 2(x – 3) = x – 2

3x + 3 – 2x + 6 = x – 2

3x – 2x – x = –3 – 6 – 2,

откуда получили бы

что невозможно. Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.

Решение рациональных уравнений сложного вида в 9-м классе

Разделы: Математика

Цели:

• Обобщить и углубить знания обучающихся по данной теме;
• Научить использовать различные методы решения: метод разложения на множители – группировки, метод замены переменной – подстановки для подведения рациональных уравнений сложного вида к более простому;
• Познакомить с различными видами рациональных уравнений: симметрических, частного случая возвратных уравнений и с методом их решения;
• Побуждать ребят к взаимоконтролю, самоконтролю и самоанализу при выполнении заданий;
• Оказывать взаимовыручку, поддержку со стороны одноклассников – ассистентов.
• Добиваться получения новых знаний через самостоятельное выполнение заданий с последующей взаимопроверкой.

Оборудование: доска раздвижная, листы – задания для устного счета, компьютер, экран.

Время: 90 минут – 2 урока.

1. Проверка домашнего задания (5 минут).

На доске (на обратной стороне) заранее на перемене учащимися записаны решения. Ученики меняются тетрадями друг с другом по парте и после проверки ставят оценки “5” – нет ошибок; “4” – 1 -2 ошибки; “3” – 3-4 ошибки, а более – “ 2”.

2. Устный тест – повторение:

На парте лежат карточки с решениями и ответы к ним, выбрать правильный ответ и объяснить почему?

задания / ответы	1	2	3	4
(х-3) (х+7)=0	3; 7	3; -7	-3;7	-3;-7
х 2 – 6х + 5 = 0	5;1	2;3	-5;-1	-2; -3
х 2 – 25 = 0	0;5	1;25	-5;5	Нет решения
х 2 + 4х + 7 = 0	3,5; 2	Нет решения	2+; 2-	1; 2,5
3(1-х)+2 = 5 – 3х	Нет решения	3;1	Множество корней	0;5

Правильные ответы: 1 задание – 2; 2 зад. – 3; 3 зад. – 3; 4 зад. – 2; 5 зад. – 3.

Учитель: Под рациональным уравнением принято понимать уравнение, которое может быть записано в виде: а_nx n + a_n-1x n-1 + … a₂x 2 + a₁x + a₀ =0, где a_n, a_n-1, …a₀ – заданные числа, а х – неизвестное. Простейшие рациональные уравнения мы решаем с помощью четырех основных методов.

(Метод перехода от равенства, связывающего функции, к равенству, связывающему аргументы; метод замены переменной; метод разложения на множители – группировки; функционально – графический метод).

Мы научились решать рациональные уравнения второй степени, а третьей, четвертой?

А каким методом вы решите уравнение вида a) х 3 – 8 + х – 2 = 0?

Подсказка: желательно подвести к произведению многочленов.

Да, верно, используем метод разложения на множители – группировки. Группируем слагаемые, применим формулы сокращенного умножения и получим произведение нескольких множителей – многочленов в левой части уравнения, а в правой – нуль.

(Вызывается ученик сильный в математике, а если нет, то показывает учитель ход решения).

б) А при таком уравнении х 3 – 3х + 2 = 0 можно использовать метод группировки?

Перепишем уравнение, записав , получим , а теперь сгруппируем (х 3 – х) – (2х -2) = 0. Дальнейшее решение самостоятельно, а один ученик выходит к доске, решает на другой стороне, затем учащиеся сверяют.

Учитель: Вспомним, при решении биквадратных уравнений какой метод мы использовали? Самый распространенный из всех методов – да, метод замены переменной – метод подстановки. Искусство производить замену переменных заключается в том, чтобы увидеть, какая замена будет более рациональна и быстрее приведет к успеху. На сегодняшнем уроке мы это и рассмотрим.

Разберем решение данного уравнения:

Освободимся от знаменателя, t 2 + 4t + 3 = 0, где t ? 0.

Дорешать самостоятельно, дальнейшее решение проецируется на экран.

По формуле решаем второе уравнение =

= = = = =

Ответ: х₁ = -5, х₂ = 1, х₃ = , х₄ = .

Учитель: Рассмотрим уравнение вида

г) (х 2 + 10х ) 2 + (х 2 + 5) 2 = 157.

Метод замены переменной легко увидеть, если воспользоваться формулой квадрата суммы для второй скобки. (х 2 + 10х ) 2 + (х 2 +10х + 25) = 157; (Далее решает ученик у доски, а остальные – самостоятельно).

Пусть тогда получим

х 2 + 10х = 11 или х 2 + 10х = -12. Решая эти уравнения, получим

Ответ: <-11; 1; -5 >. +

Учитель: Рассмотрим уравнение вида

Найдем равенство сумм пар чисел -7 + 2 = -1 – 4,

Перемножим между собой первую и третью, вторую и четвертую скобки, получим (х 2 – 5х – 14) ((х 2 – 5х + 4) – 40.

Введем замену: х 2 – 5х – 14 = t, где t – любое число, получим t(t + 18) = 40, t 2 + 18t – 40 = 0.

(Работает учитель, показывая ход решения или ученик с помощью учителя).

Решим данное уравнение по т. Виета

Решим систему уравнений

Ответ: х₁ = 2, х₂ = 3, х₃ = х₄ =

Проверка решения данного уравнения с помощью проекции решения на экране.

+1 + 4 = + 2+ 3. Данное условие равенства выполняется, поэтому раскроем скобки, группируя первый множитель с последним и второй с третьим.

Тогда данное уравнение примет вид: (х 2 + 5х + 4) (х 2 + 5х +6) = 24.

Полагая х 2 + 5х = t, получим квадратное уравнение (t +4)(t +6) = 24,

решая его t 2 + 10t =0, t(t + 10) =0, найдем корни t₁ =0, t₂= -10.

Затем решаем уравнения

Учитель: Уравнения вида а₀х n + a₁x n-1 + … + a_kx k + … + a₁x + a₀ = 0, где коэффициенты членов, равно от стоящих от концов, равны между собой, называют симметрическими уравнениями.

Симметрические уравнения обладают следующими свойствами:

1. Симметрическое уравнение нечетной степени имеет корень х = -1, в чем можно убедиться непосредственной подстановкой;

2. Уравнение четной степени 2n решаются с помощью подстановки

V = x + сводится к уравнению степени n.

Данное уравнение симметрическое, так как коэффициенты равно отстоящих от концов, равны между собой. Степень уравнения нечетная равная 5, поэтому корень данного уравнения х = – 1.

Пусть Разделим левую часть уравнения на х + 1 и получим симметрическое уравнение четвертой степени:

Разделим обе части уравнения на х 2 : 2х 2 + 3х – 16 + 3• + 2• 1/х 2 = 0, и сгруппируем члены уравнения: 2(х 2 + 1/х 2 ) + 3 (1 + ) – 16 = 0.

Используем метод замены переменной при t = x + , возведем в квадрат обе части уравнения, получим t 2 = (x + ) 2 = x 2 + 2• x • + 1/x 2 , тогда x 2 + 1/x 2 = t 2 – 2, и после преобразований получим квадратное уравнение 2 t 2 + 3t – 20 = 0. Находим корни t = = = t₁ = , t₂ = -4. Таким образом , исходное уравнение четвертой степени равносильно совокупности уравнений x + и x + = -4.

Решив данные уравнения, получим еще четыре корня исходного уравнения.

Ответ: х₁ = -1, х₂ = -2+, х₃ = -2 – , х₄ = 2, х₅ = .

Учитель: Прошу вас, ребята, решить самостоятельно с последующей проверкой симметрическое уравнение четвертой степени. А почему оно симметрическое?

з) 2х 4 + 3х 3 – 16 х 2 + 3х + 2 = 0.

Разделим обе части уравнения на х 2 , получим 2х 2 + 3х – 16 + + 2/х 2 =0.

Сгруппируем (2х 2 + 2/х 2 ) + (3х+ ) – 16 = 0, 2(х 2 +12/х 2 ) + 3(х+ ) – 16 =0.

Введем метод замены переменной, обозначим х+ = t, возведем в квадрат обе части равенства, получим t 2 = (x + ) 2 = x 2 + 2• x • + 1/x 2 , тогда x 2 + 1/x 2 = t 2 – 2, и после преобразований получим квадратное уравнение вида 2(t 2 – 2) + 3t – 16 =0. Решая уравнение по общему виду 2t 2 -4 + 3t -16 = 0, 2t 2 + 3t – 20 = 0, получим корни t₁ = , t₂ = -4. Можно не решать, а сразу же записать ответы предыдущего уравнения.

Ответ: х₁ = , х₂ = -2+, х₃ = -2 – , х₄ = 2.

Учитель: Мы рассмотрели симметрические уравнения, являющиеся частным случаем возвратных уравнений. Следовательно, и ход их решения будет похожим, но более подробно мы познакомимся с возвратными уравнениями и рассмотрим более подробно ход решения на следующем занятии. А сейчас,

я вам предложу домашнее задание на два варианта для самостоятельного решения. Дополнительно даны ответы ко всем уравнениям. Не сможете справиться, рассмотрим на уроке. а кто-то хочет больше решить, с довольствием приветствую вас.

Вариант 1.	Вариант 2.
а) (х 2 – 6х) 2 -2(х – 3) 2 = 81; б) х 3 + х + 2 = 0; в) 6х 4 – 35 х 3 + 62 х 2 – 35х + 6 = 0; г) (х –1)(х+2)(х-3)(х+4) = 144; д) (х 2 + х + 1)(х 2 + х + 2) = 12;	а) (х 2 – 8х) 2 + 3(х – 4) 2 = 76; б) х 3 + 3х 2 + 2х = 0. в) 5х 4 – 12х 3 + 14х 2 – 12х + 5 = 0. г) (х-1)(х-2)(х-3)(х-4) = 15. д) (3х +2) 4 – 13(3х + 2) 2 + 36 = 0.

Выберите ответы, выполняя домашнее задание.

А

В. 1.

С < -2; -1; 0>.

Д < -2; 1>.

Б<0; 1>.

Учитель: Подведем итог нашей темы. Уравнения третьей и четвертой степени решались в общем случае методом замены переменной, в который заключается в том, что для решения уравнения вида f(x) =0 вводят переменную t = g(x) и выражают f(x)через t, получая новое уравнение w(t) = 0. Решая затем уравнение w(t)= 0, находят его корни1, t₂, … t_n>. После чего получают совокупность n – уравнений g(x) = t₁, g(x) = t₂, … g(x) = t_n, из которых находят корни исходного уравнения.

Учим алгебра 7 класс. Как решать уравнения алгебра 7 класс, примеры, дроби, функции, степени, модули

В 7 классе ученикам предстоит научиться решать уравнения, дроби, строить функции, разбираться в модулях. Для этого следует познакомиться с основными понятиями в темах, рассмотреть алгоритм решения и пошагово учиться находить ответы. Главное правило — начать с простых примеров, постепенно переходя на более сложные. Большинство задач можно решать несколькими методами (это касается и примеров), следует выбрать самый простой и удобный для себя.

Как решать уравнения алгебра 7 класс

Начнем с решения линейных уравнений (на рисунке показано, по какому принципу они устроены). Чтобы найти ответ в таких уравнениях, нужно совершать действия: раскрытие скобок, поиск подобных слагаемых, умножение/деление частей на одно и тоже число, перенос слагаемых из одной части уравнения в другую. Всё зависит от конкретного примера.

Рассмотрим несколько примеров пошагового решения линейных уравнений.

Пример 1.
6x + 24 = 0

Поскольку части уравнения (левая и правая) равны, то можно отнять из каждой одинаковое число. Равенство не изменится, а пример станет значительно проще. В представленном уравнении отняли 24 и слева, и справа. В левой части 24 сократилось, а в правой (0 — 24) получилось -24 (не забываем ставить знак минуса).

Получилось: 6x = -24. Теперь можем сократить 6 и -24 на число 6 (или рассуждаем так: чтобы найти множитель, нужно произведение разделить на другой множитель). В ответе будет -4. Не забудьте в самом конце подставить полученное число вместо х. Совпал ответ — значит, все правильно.

Можно рассуждать проще: чтобы упростить уравнение, нужно из левой части отправить в правую число 24, поменяв его знак. Равенство сохранится (на рисунке ниже).

Пример 2.
9 + 16x = 41 + 14x

Это уравнение более сложное. Здесь важно запомнить несколько моментов:

• числа без х переносятся в левую часть, а с х — в правую;
• при переносе знаки меняют.

Пример 3.
7(10 — 4x) + 5x = 12 — 3(5x + 2)

1. Раскрыть скобки, выполнив умножение: 7 умножаем на каждое число в скобках (в правой части -3 на каждое). При выполнении действия не забывайте сохранять знаки.
2. Записываем уравнение, получившееся после раскрытия скобок. Ещё раз сверяем знаки.
3. Числа с х отправляются в левую часть, без х — в правую. Знаки чисел, которые переходят в другую часть, меняем.
4. Подсчитываем результат с обеих сторон.
5. Делим -64 на -8 и получаем ответ. Не забываем, что минус на минус при делении и умножении дают плюс.

В рассмотренных уравнениях корень точно определён. Так получается не всегда.

Пример 4.

Обратите внимание, в ответе получилось 0x = 0. Это значит, что x может быть любым числом, потому что при умножение хоть какого числа на 0 получится 0.

В этом примере корней нет, так как любое число, которое умножают на 0, будет равно 0 (21 никак не получится).

Как решать систему уравнений алгебра 7 класс

Системой называют несколько уравнений, в которых нужно найти такие значения неизвестных, чтобы равенство сохранилось. Разберемся на примерах, как выглядят системы и какие методы их решения существуют.

метод подстановки

Из самого названия следует, что алгоритм требует что-то подставлять. Ниже представлена система, где нужно найти значения x и y.

Суть метода подстановки: переменную в одном из уравнений выражают через другую переменную. Затем подставляют полученное выражение в другое уравнение.

Смотрим на систему. Видим, что удобнее будет выразить x во втором уравнении (так как он один). Выражаем путем переноса за знак «равно» 12y. Получилось: x = 11 — 12y (не забываем менять знак при переносе числа).

В первое уравнение вместо «x» записываем получившееся выражение. Меняем только x, остальное сохраняется в прежнем виде.

Далее преобразуем уравнение, в которое поместили выражение. Раскрываем скобки (перемножаем 5 на каждое значение). y оставляем в левой части, числа переносим в правую, знаки меняем. Таким образом нашли значение y (y = 1).

Теперь подставляем полученную единицу во второе уравнение (x = 11 — 12y).

Убедиться в правильном решение можно так: подставьте полученные значения в систему. Если равенства сохранятся, значит, решено верно.

метод сложения

Чтобы решить систему методом сложения, нужно из двух уравнений сделать одно. Просто складываем первое и второе. Здесь «y» просто сократились, и получилось простое уравнение. Как только нашли значение «х», нужно подставить его в любой пример (здесь поставили во второе уравнение). В ответе пишется так: (4; 3) — первым всегда пишется х, затем у.

графический метод

У нас есть система, где y = 5x и y = -2x + 7. Рассмотрим алгоритм решения системы уравнений:

1. Подбираем 2 числа для х. Мы взяли 0 и 1, подставляем в первое уравнение: y = 5 * 0 = 0; у = 5 * 1 = 5. Значит первая прямая имеет координаты: (0; 0) и (1; 5).
2. Для второго уравнения подбираем значения х. Взяли 3 и 2, подставляем и находим у: -2 * 3 + 7 = 1; -2 * 2 + 7 = 3. Значит прямая имеет координаты (3; 1) и (2; 3).
3. Отмечаем на графике соответствующие прямые, подписываем их название.
4. на месте пересечения получившихся прямых ставим точку — это будет решение.
5. Точка имеет координаты (1; 5).

На заметку! Старайтесь подбирать такие значения х, чтобы у был небольшим. Так отмечать будет проще.

Выбирайте самый удобный способ решения. Третий метод — графический, считают самым неточным.

Как решать дроби 7 класс

Дроби можно разделить на 2 основных вида:

Они различаются в способе написания (смотрите рисунок ниже). В свою очередь и те, и другие делятся еще на несколько видов.

Для начала рассмотрим решение примеров с десятичными дробями.

Особое внимание при решении стоит уделить запятым. При сложении и вычитании запятые стоят строго друг под другом, при умножении это не имеет значения.

Примеры решения обыкновенных дробей.

• при сложении и вычитании нужно привести дроби к общему знаменателю, найти дополнительные множители. Так, для чисел 6 и 4 общим знаменателем стало число 24. Дополнительные множители считали так: 24 : 6 = 4 (для первой дроби) и 24 : 4 = 6 (для второй). Потом умножили доп. множители на числители и полученные числа сложили. Если в ответе получилась неправильная дробь, то выделяем целую часть, при необходимости сокращаем дроби.
• при умножении пишем дроби под одной чертой, сокращаем.
• при делении нужно вторую дробь перевернуть, поставить знак умножения и сократить дроби.

Если пример состоит из простой и десятичной дроби, то следует привести их к одному виду (к которому проще или удобнее считать).

Примеры 7 класс как решать

Теперь закрепим решение дробей на примерах.

Решение примера, представленного ниже:

1. Видим, что присутствует как обыкновенная дробь, так и десятичные. Нужно привести к одному виду. Так как десятичных больше, и превратить 1/4 в этот вид проще, то делим 1 на 4, а целую часть сохраняем. Вышло 5,25.
2. Далее умножаем — 3 на каждое число в скобках, внимательно следим за знаками.
3. Остается от 10,4 отнять 9,3. В итоге вышло 1,1.

Но можно было решить проще. Первое действие всегда в скобках. Поэтому от 5,25 отнимаем 2,15. Получится 3,1. Умножаем ее на 3 — вышло 9,3. И отнимаем: 10,4 — 9,3 = 1,1. Этот способ даже проще, потому что не нужно следить за знаками при раскрытии скобок.

Чтобы верно решить следующий пример, нужно:

• точно проставить порядок действий (умножение и деление делаем в первую очередь, затем складываем);
• Умножить десятичные дроби столбиком, не забыть поставить запятую;
• деление здесь простое: переставили запятую на один знак вправо, поделили, получили -2.
• сложили числа.

Как решать задачи алгебра 7 класс

Задачи решаются путем составления уравнений.

Другие примеры задач с подробными решениями в видео-материалах.

Как решать функции алгебра 7 клас с

Функцией принято считать зависимость y от x. При этом x является переменной (или аргументом), а у — это значение функции (зависимая переменная).

• y(x) = 8x
• y(x) = −3x — 62
• y(x) = x−1 + 18

Чтобы найти значение у, которое бы соответствовало определенному значению х, нужно просто это значение х подставить в функцию.

Как решать степени алгебра 7 класс

Если требуется взять какое-либо число несколько раз, то проще записать его в степени. Например, нужно двойку взять три раза, т. е.: 2 * 2 * 2. Получается длинная запись. Поэтому придумали писать так: 2³ (читается: два в третьей степени).

Чтобы число возвести в степень (она указывается справа от числа вверху), нужно его умножать на самого себя столько раз, какая цифра указана. Рассмотрим подробнее на примерах.

Не всегда получается возвести число в степень «в уме». Иногда посчитать сложно. Например, возвести 6 в 5 степень, быстро получится не у каждого. Чтобы всякий раз не считать столбиком, лучше выучить основные степени. Они представлены в таблице.

При возведении любого числа в степень 1, получится это же число. Если возводить число в нулевую степень, в ответе будет 1.

Рассмотрим несколько примеров со степенями.

Отдельное внимание обращаем на возведение в степень отрицательного числа. Если такое число возводить в четную степень (2; 4; 6 и т.д.), то получится положительный ответ, если в нечетную, то ответ со знаком минус.

Алгебра модули как решать

Модулем числа называют это же число, только без знака минус. Например: | − 9 | = 9. При этом если число изначально неотрицательное, то оно остается прежним.

Перейдем к простым примерам.

Логично предположить, что под модулем будет число 4. Также подойдет число -4, ведь из-под модуля все равно выйдет положительное. Так, корнями уравнения будут: x = 4 и x = − 4.

Из-под модуля не может выйти отрицательное число. Поэтому, если видим что-то похожее: Ι-8 + хΙ = -8, значит, корней не будет, так как уравнение заведомо нерешаемо.

Другие примеры описаны в видео.

Об Авторе

Смотрите также

Подарок маме на 8 марта своими руками, какую сделать поделку для мамы: в детском саду, в школе, лучшие поделки своими руками. Рисунок маме 8 марта: рисование простые рисунки

Частушки смешные детские про: учителей, школьников, школу, про воспитателей, про детский сад, народные, русские, прикольные детские. Смешные новогодние частушки для детей

Сложные логические загадки с ответом с подвохом, загадки на логическое мышление: для взрослых, для детей

2 комментария

Спасибо большое очень помогли.

Огромное спасибо!А то учитель неможет нормально тему объяснить