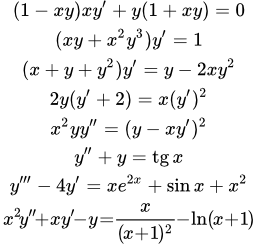Сложные дифференциальные уравнения второго порядка

Примеры дифференциальных уравнений с решениями

• Попробуйте решить приведенные ниже дифференциальные уравнения.
• Нажмите на изображение уравнения, и вы попадете на страницу с подробным решением.

Примеры решений дифференциальных уравнений первого порядка

Примеры решений дифференциальных уравнений второго и высших порядков

Найти общее решение дифференциального уравнения, или решение с заданными начальными условиями.

Примеры решений линейных дифференциальных уравнений с постоянными коэффициентами

Примеры решений линейных уравнений в частных производных первого порядка

Найти общее решение линейного однородного уравнения в частных производных первого порядка и решить задачу Коши с указанным граничным условием:
,
при .

Найти поверхность, удовлетворяющую данному уравнению
,
и проходящую через данную окружность
, .

Автор: Олег Одинцов . Опубликовано: 28-01-2016 Изменено: 26-11-2021

Примеры решений задач по дифференциальным уравнениям

Теперь, когда вы научились находить производные и интегралы, самое время перейти к более сложной теме: решению дифференциальных уравнений (они же дифуры, диффуры и диф.уры :)), то есть уравнений, которые вместе с самой функцией (и/или аргументом), содержат и производную или даже несколько.

Как же решать дифференциальные уравнения? Главное, что понадобится, это а) умение правильно определить тип дифференциального уравнения и б) умение хорошо интегрировать — это существенная часть работы. А дальше следовать алгоримам для каждого из типов уравнений, которые подробно описаны в учебниках и ниже в примерах.

В этом разделе вы найдете решенные задачи на составление и решение дифференциальных уравнений. Примеры решений дифуров выложены бесплатно для вашего удобства и отсортированы по темам — изучайте, ищите похожие, решайте свои. Есть трудности в выполнении заданий? Мы готовы оказать помощь по дифференциальным уравнениям

Как решить дифференциальное уравнение онлайн?

Да ладно, неужели только вручную? Мучиться, определять тип, переносить, интегрировать, заменять, снова интегрировать, подставлять, выводить? Наверняка ведь есть онлайн-калькуляторы, которые позволяют решать дифференциальные уравнения?

У меня две новости, хорошая и плохая. Хорошая в том, что действительно самые распространенные типы дифференциальных уравнений математические программы умеют решать. Плохая в том, что обычно они выводят ответ (для научных расчетов этого достаточно), а не полное решение.

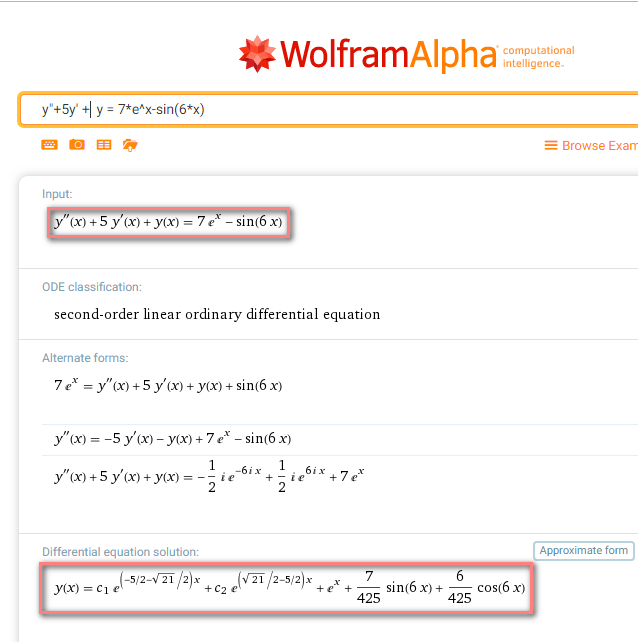
Есть известный математический сервис www.wolframalpha.com, которые представляет полные решения множества математических задач, в том числе диффуров онлайн (на английском языке) за 7 долларов в месяц. Ответы же доступны всем и могут помочь проверять правильность своего решения (см. ниже на скриншоте обведено само уравнение и его решение). Подробнее об этом сайте и типичных задачах, решаемых на нем, вы можете узнать тут.

Если вы забьете в поисковик что-то вроде «решить дифференциальное уравнение онлайн», то получите десятки ссылок на сайты, обещающие именно это.

Я проверила все сайты с первых страниц Яндекса и Гугла. Большая часть сайтов использует результаты расчетов www.wolframalpha.com (см. выше) и показывает вам ответ (и рекламу :)). Некоторые при этом не показывают даже ответа или говорят, что уравнение введено некорректно (хотя это вполне стандартное решаемое вручную линейное уравнение с постоянными коэффициентами). Полное решение не выдал ни один сайт.

Выводы? Бесплатно и полно и онлайн — не бывает. Хотите получать полные решения — используйте платную подписку на ВольфрамАльфа (или проконсультируйтесь у нас). Хотите ответы — там же бесплатно. Хотите научиться решать? Придется засучить рукава. Примеры на этой странице и ссылки внизу помогут вам. Удачи!

Общий интеграл, семейство кривых

Задача 1. Показать, что функция $y^2-x^2-Cy=0$ является общим интегралом дифференциального уравнения $y'(x^2+y^2)-2xy=0.$

Задача 2. Составить дифференциальное уравнение семейства кривых $C_1 x+(y-C_2)^2=0.$

Решения дифференциальных уравнений 1 порядка

Задача 3. Найти общее решение линейного дифференциального уравнения первого порядка $ xy’+x^2+xy-y=0.$

Задача 4. Решить однородное дифференциальное уравнение $y’=-y/x \quad (x \ne 0).$

Задача 5. Решить дифференциальное уравнение $(y^4-2x^3y)dx+(x^4-2xy^3)dy=0.$

Задача 6. Решить однородное дифференциальное уравнение $(2x+y+1)dx+(x+2y-1)dy=0.$

Задача 7. Решить линейное дифференциальное уравнение первого порядка $y’-2xy=3x^2-2x^4.$

Задача 8. Решить дифференциальное уравнение $(x+y^2)y’=y-1.$

Решение задачи Коши для ДУ

Задача 9. Решить дифференциальное уравнение с разделяющимися переменными $(1+x^2)dy-2xydx=0.$ Найти частное решение, удовлетворяющее начальному условию $y(0)=1$.

Задача 10. Решить задачу Коши для дифференциального уравнения второго порядка $2y y» +1 =(y’)^2, \, y(1/3)=1, \, y'(1/3)=2$.

Задача 11. Найти решение задачи Коши для дифференциального уравнения $$ y’= \frac<2y-x><2x+y>, y(1)=1. $$

Задача 12. Решить задачу Коши для дифференциального уравнения третьего порядка $$ y»’=x+\cos x, \quad y(0)=0, y'(0)=0, y»(0)=0. $$

Решения дифференциальных уравнений 2 порядка

Задача 13. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами $y»+4y’+4y=xe^<2x>.$

Задача 14. Решить задачу Коши для дифференциального уравнения второго порядка с постоянными коэффициентами методом вариации: $$ y»-3y’=\frac<9e^<-3x>><3+e^<-3x>>, \quad y(0)=4\ln 4, y'(0)=3(3\ln 4-1). $$

Cоставление дифференциальных уравнений

Задача 15. Скорость остывания нагретого тела пропорциональна разности температур тела и окружающей среды. За 10 минут тело охладилось от 100 до 60 градусов. Температура среды постоянна и равна 20 градусам. Когда тело остынет до 25 градусов?

Задача 16. Моторная лодка движется в спокойной воде со скоростью 5 м/сек. На полном ходу ее мотор выключается и через 40 сек после этого скорость лодки уменьшается до 2 м/сек. Определить скорость лодки через 2 минуты после остановки мотора, считая, что сопротивление воды пропорционально скорости движения лодки.

Решения нелинейных дифференциальных уравнений

Задача 17. Решить дифференциальное уравнение $y^2 ^2 -2xyy’+2y^2-x^2=0.$

Задача 18. Решить дифференциальное уравнение $^2-4xyy’+8y^2=0.$

Линейные дифференциальные уравнения второго порядка

Данная статья раскрывает смысл нахождения и алгоритм для общего решения линейных однородных и неоднородных дифференциальных уравнений второго порядка с подробным просмотром их решений.

Линейное однородное уравнение второго порядка имеет вид y » + p ( x ) · y ‘ + q ( x ) · y = 0 , неоднородное — y » + p ( x ) · y ‘ + q ( x ) · y = f ( x ) . F ( x ) , p ( x ) и q ( x ) являются функциями, которые непрерывны из интервала интегрирования x . Частным случаем принято считать p ( x ) = p и q ( x ) = q , то есть при наличии постоянных в записи функции.

Нахождение общего решения линейных дифференциальных уравнений

Общее решение y 0 для линейного однородного дифференциального уравнения (ЛОДУ) вида y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 0 ( x ) · y = 0 из интервала x при наличии постоянных коэффициентов f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) , располагаемых на x , считают линейную комбинацию n линейно независимых частных решений ЛОДУ y j , j = 1 , 2 , . . . , n , где имеются произвольные коэффициенты C j , j = 1 , 2 , . . . , n , то есть y 0 = ∑ j = 1 n C j · y j .

Общим решением y для линейного неоднородного дифференциального уравнения вида y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 0 ( x ) · y = f ( x ) из интервала x при наличии коэффициентов f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) и функции f ( x ) является сумма вида y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 0 ( x ) · y = 0 , где y

считается одним из общих решений ЛНДУ.

Отсюда следует, что

• выражение y 0 = C 1 ⋅ y 1 + C 2 ⋅ y 2 считается общим решением дифференциального уравнения y » + p ( x ) · y ‘ + q ( x ) · y = 0 , а y 1 и y 2 считаются линейно независимыми частными решениями;
• y = y 0 + y

обозначают в качестве общего решения уравнения y » + p ( x ) · y ‘ + q ( x ) · y = f ( x ) , где y

принимает одно из любых частных решений, y 0 соответствует общему решению ЛОДУ.

После чего необходимо находить y 1 , y 2 и y

Если функции простые, то применяется метод подбора.

Линейно независимые функции y 1 и y 2 находятся из

1 ) 1 , x , x 2 , . . . , x n 2 ) e k 1 · x , e k 2 · x , . . . , e k n · x 3 ) e k 1 · x , x · e k 1 · x , . . . , x n 1 · e k 1 · x , e k 2 · x , x · e k 2 · x , . . . , x n 2 · e k 2 · x , . . . e k p · x , x · e k p · x , . . . , x n p · e k p · x .

Линейную независимость проверяют определителем Вронского вида W ( x ) = y 1 ( x ) y 2 ( x ) y 1 ‘ ( x ) y 2 ‘ ( x ) . Когда функции располагаются на интервале х , тогда такой определитель не равен 0 на заданном промежутке.

Когда имеются функции вида y 1 = 1 и y 2 = x , где x принадлежит множеству действительных чисел, то W ( x ) = 1 x 1 ‘ x ‘ = 1 x 0 1 = 1 ≠ 0 ∀ x ∈ R .

Функции вида y 1 = sin x и y 2 = cos x считаются линейно независимы на области действительных чисел, потому как W ( x ) = sin x cos x ( sin x ) ‘ ( cos x ) ‘ = sin x cos x cos x — sin x = = — sin 2 x — cos 2 x = — 1 ≠ 0 ∀ x ∈ R

Функции y 1 = — x — 1 и y 2 = x + 1 считаются линейно независимыми из интервала ( — ∞ ; + ∞ )

W ( x ) = — x — 1 x + 1 — x — 1 ‘ ( x + 1 ) ‘ = — x — 1 x + 1 — 1 1 = = — x — 1 + x + 1 = 0 ∀ x ∈ R

Не всегда можно подобрать y 1 , y 2 , y

. Поэтому следует использовать другой метод. При наличии ненулевого частного решения y 1 ЛОДУ второго порядка y » + p ( x ) · y ‘ + q ( x ) · y = f ( x ) , тогда общее решение находится понижением степени и подстановкой y = y 1 · ∫ u ( x ) d x .

Найти общее решение уравнение вида y » — y ‘ + y x = 0 .

Решение

Частное решение записывается как y 1 = x для дифференциального уравнения y » — y ‘ + y x = 0 , когда x не равен 0 . Необходимо перейти к понижению степени при помощи постановки. Тогда получим уравнение вида y = y 1 · ∫ u ( x ) d x = x · ∫ u ( x ) d x , а итоговое значение примет вид интеграла ∫ u ( x ) d x = y x .

По правилу дифференцирования произведения и свойству неопределенного интеграла получаем выражение вида

y ‘ = x · ∫ u ( x ) d x ‘ = x ‘ · ∫ u ( x ) d x + x · ∫ u ( x ) d x ‘ = = ∫ u ( x ) d x + x · u ( x ) = y x + x · u ( x ) y » = ∫ u ( x ) d x + x · u ( x ) ‘ = ∫ u ( x ) d x ‘ + x ‘ · u ( x ) + x · u ‘ ( x ) = = 2 u ( x ) + x · u ‘ ( x )

Производим подстановку в исходное выражение. Запишем равенство вида:

y » — y ‘ + y x = 0 ⇔ 2 u + x · u ‘ — y x — x · u + y x = 0 ⇔ 2 u + x · u ‘ — x · u = 0 ⇔ x · d u d x + u · — x + 2 = 0 ⇔ d u u = 1 — 2 x d x , u = 0

Интегрируем обе части выражения и получаем, что ln u + C 1 = x — 2 ln x + C 2 ⇔ ln u = x + ln 1 x 2 + C 2 — C 1 . Переходим к записи общего вида выражения. Тогда она примет вид u = C · e x x 2 с C являющейся произвольной постоянной.

Ответ: из выражения y = x · ∫ u d x очевидно, что общее решение заданного ЛОДУ примет вид y = x · C · ∫ e x x 2 d x = x · C · ( F ( x ) + C 3 ) , когда F ( x ) считается одной из первообразных функции e x x 2 .

Для решения неоднородного дифференциального уравнения y » + p ( x ) · y ‘ + q ( x ) · y = f ( x ) нужно подбирать y

, если возможно найти y 1 и y 2 . Поиск общего решения производится при помощи метода вариации произвольных постоянных.

В таком случаем ЛОДУ принимает вид y 0 = C 1 ⋅ y 1 + C 2 ⋅ y 2 . Преобразовывая произвольные постоянные для общего решения, ЛНДУ принимает вид y 0 = C 1 ( x ) ⋅ y 1 + C 2 ( x ) ⋅ y 2 , где производные неизвестных функций C 1 ( x ) и C 2 ( x ) можно определить из системы вида C 1 ‘ ( x ) · y 1 + C 2 ‘ ( x ) · y 2 = 0 C 1 ‘ ( x ) · y 1 ‘ + C 2 ‘ ( x ) · y 2 ‘ = f ( x ) , а получение самих функций производится путем интегрирования.

Найти общее решение уравнения y » — y = 2 x .

Решение

Для решения необходимо обратить внимание на его частные решения. Для ЛОДУ y » — y = 0 они являются y 1 = e — x и y 2 = e x , то есть выражение вида y 0 = C 1 · e — x + C 2 · e x . Изменяя постоянные, общее решение получит вид

y = C 1 ( x ) · e — x + C 2 ( x ) · e x .

Необходимо составить систему линейных уравнений и решить

C 1 ‘ ( x ) · y 1 + C 2 ‘ ( x ) · y 2 = 0 C 1 ‘ ( x ) · y 1 ‘ + C 2 ‘ ( x ) · y 2 ‘ = f ( x ) ⇔ C 1 ‘ ( x ) · e — x + C 2 ‘ ( x ) · e x = 0 — C 1 ‘ ( x ) · e — x + C 2 ‘ ( x ) · e x = 2 x

Чтобы разрешить ее, следует применить метод Крамера. Тогда

∆ = e — x e x — e — x e x = e — x · e x + e — x · e x = 2 ∆ C 1 ‘ ( x ) = 0 e x 2 x e x = — ( 2 e ) x ⇒ C 1 ‘ ( x ) = ∆ C 1 ‘ ( x ) ∆ = — 1 2 · 2 e x ∆ C 2 ‘ ( x ) = e — x 0 — e — x 2 x = 2 e x ⇒ C 2 ‘ = ∆ C 2 ‘ ( x ) ∆ = 1 2 · 2 e x

После интегрирования полученных выражений для того, чтобы найти C 1 ( x ) и C 2 ( x ) , запишем, что

C 1 ( x ) = — 1 2 · ∫ ( 2 e ) x d x = — 1 2 · ( 2 e ) x ln ( 2 e ) + C 3 = = — 1 2 · ( 2 e ) x ln 2 + 1 + C 3 C 2 ( x ) = 1 2 · ∫ 2 e x d x = 1 2 · 1 ln 2 e · 2 e x + C 4 = = 1 2 · 1 ln 2 — 1 · 2 e x + C 4

Ответ: общим решением для заданного уравнения получим уравнение вида

y = — 1 2 · ( 2 e ) x ln 2 + 1 + C 3 · e — x + 1 2 · 1 ln 2 — 1 · 2 e x + C 4 · e x .

Итоги

• Поиск общего решения ЛОДУ 2 порядка y » + p ( x ) · y ‘ + q ( x ) · y = 0 выполняется из y 0 = C 1 ⋅ y 1 + C 2 ⋅ y 2 , где y 1 и y 2 считаются линейно независимыми частными решениями. Для подбора частных решений y 1 и y 2 чаще всего начинается с нахождения общего дифференциального уравнения y » + p ( x ) · y ‘ + q ( x ) · y = 0 . Когда подбор невозможен, тогда производится снижение порядка с помощью замены y = y 1 · ∫ u ( x ) d x , причем его решение приведет к общему виду ЛОДУ второго прядка.
• Поиск общего решения ЛНДУ 2 порядка вида y » + p ( x ) · y ‘ + q ( x ) · y = f ( x ) производится с помощью y = y 0 + y

является любым частным решением, а y 0 считают в качестве общего решения ЛОДУ. Нахождение y 0 _, то есть общего дифференциального уравнения y » + p ( x ) · y ‘ + q ( x ) · y = 0 , производится первоначально. После чего производится подбор y

. Если необходимо, то в начале производится подбор y 1 и y 2 для определения общего решения ЛНДУ с помощью применения метода вариации произвольных постоянных.