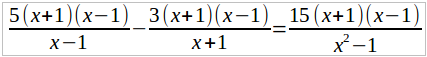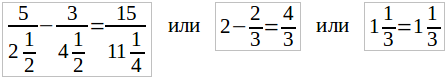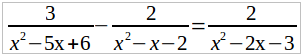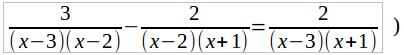Сложные уравнения по алгебре 11

Итоговое повторение темы «Решение уравнений» в курсе алгебры 11-го класса

Разделы: Математика

На первом, мотивационном этапе с учащимися обговорили, почему и для чего необходимо повторить эту тему. Дали оценку своих возможностей, составили план предстоящей работы:

повторить тему за 6 уроков.
повторить тему «Общие сведения об уравнениях»; (1 ч)
обратить внимание на виды уравнений; (1 ч)
повторить теоремы равносильности уравнений; (1 ч)
повторить способы решений уравнений. (1 ч)

Способы решения уравнений, которые предлагаются учащимися в школьных учебниках, усваиваются достаточно хорошо. Поэтому при повторении мы решили пользоваться различными пособиями по элементарной математике.

В процессе повторения ученики должны последовательно перейти от одного уровня математической деятельности к следующему, более высокому, сделав для себя открытия в этой теме.

Какова мотивация учащихся? Готовиться к выпускным экзаменам и вступительным экзаменам в вузы, расширять и углублять знания по этой теме.

Учащиеся получили творческую работу: подобрать из разных источников такие уравнения, которые выходили бы за рамки традиционных уравнений, предлагаемых в школьных учебниках.

В результате выполнения этой работы мы решили рассмотреть 13 уравнений.

Учащиеся должны были поработать дома с этими уравнениями и выполнить задания.

Задание №1.Провести классификацию уравнений по методам решения.
Задание №2. Провести классификацию уравнений по виду.
Задание №3. Решить уравнения (кто, сколько пожелает на выбор и объединиться в группы по методам решения уравнений).

Урок-семинар (2 часа)

Тема: «Решение уравнений».

Повторить и расширить сведения об уравнениях и способах их решения;
Формировать умения выполнять обобщения и конкретизацию, правильно отбирать способы решения уравнений;
Развивать качества мышления, гибкость, целенаправленность, рациональность, воспитание чувства ответственности за коллектив в процессе творческой работы.

Формы организации познавательной деятельности:

по источнику приобретенных знаний:

по уровню познавательной активности:

Организационный момент;
Актуализация опорных знаний;
Работа в творческих группах;
Защита каждой группой своего способа решения уравнений;
Зачетная работа;
Домашнее задание;
Итог урока.

Ход урока

1. Организационный момент: Девиз урока:

Посредством уравнений, теорем
Он уйму разрешал проблем.
И засуху предсказывал, и ливни
Поистине его познанья дивны.
Генрих Госсен.

2. Актуализация опорных знаний:

В результате выполнения первого задания получилась схема классификации уравнений.

Классификация уравнений по виду

При выполнении задания № 2 выяснили, что данные уравнения можно решить:

Разложением на множители (№ 1, 2, 4);
Заменой переменных (№ 4, 5, 6. 7, 10);
Однородные (№ 8,13);
Использование свойств функции(№ 3, 9. 11, 12)

3. Работа в творческих группах.

Класс разбивается на четыре группы (в каждой группе 5 учеников).

После того как каждой группе дано задание, идет обсуждение и поиск решения уравнений. Группа решает: какое уравнение, и кто представляет решение у доски для всего класса.

4. Представление и защита своего задания каждой группой.

Представили уравнение Решили методом разложения на множители.

Сгруппировали

Ответ:

Рассуждали так: Если раскрыть скобки получится уравнение 4-ой степени. Нужно найти делители свободного члена, разложить на множители левую часть и найти 4 корня уравнения, но это не рационально.

Предложили решить это уравнение способом замены переменной.

Пусть

Получили уравнение

Решим его как квадратное относительно t. Получим t =4x или t = x. Исходное уравнение распадается на совокупность двух уравнений:

Ответ: -1; 9;

Представили показательное уравнение, сводящееся к однородному.

Перепишем уравнение в виде

Получилось уравнение однородное относительно . Разделим обе части уравнения на

Пусть , причем >0. Получим , откуда

Вернемся к исходной переменной и решим уравнения

Ответ:

Представили уравнение: Это уравнение можно решить вполне стандартным способом. Но мы применили свойство монотонности функции. В левой части уравнения – возрастающая функция, в правой части — убывающая функция. Следовательно, данное уравнение не может иметь более одного корня. Число 5- корень уравнения, что проверяется подстановкой.

5. Зачетная работа:

6 Итог урока.

7. Задание на дом

№ 120 (1; 7;17) №129 (3;4)№130 (1; 3) учебник Алгебра и начала анализа. Н. Я. Виленкин и др.

С зачетной работой справились все 20 учащихся класса.

В результате проделанной работы ученики испытали радость победы над трудностями, преодоленными ими, познали новые (для них) приемы решений уравнений, дали самооценку своей деятельности и убедились, что только кропотливая самостоятельная работа приводит к формированию глубокого познавательного интереса к учебной деятельности.

Математика

52. Более сложные примеры уравнений.
Пример 1 .

5/(x – 1) – 3/(x + 1) = 15/(x 2 – 1)

Общий знаменатель есть x 2 – 1, так как x 2 – 1 = (x + 1)(x – 1). Умножим обе части этого уравнения на x 2 – 1. Получим:

или, после сокращения,

5(x + 1) – 3(x – 1) = 15

5x + 5 – 3x + 3 = 15

Рассмотрим еще уравнение:

5/(x-1) – 3/(x+1) = 4(x 2 – 1)

Решая, как выше, получим:

5(x + 1) – 3(x – 1) = 4
5x + 5 – 3x – 3 = 4 или 2x = 2 и x = 1.

Посмотрим, оправдываются ли наши равенства, если заменить в каждом из рассмотренных уравнений x найденным числом.

Для первого примера получим:

Видим, что здесь нет места никаким сомнениям: мы нашли такое число для x, что требуемое равенство оправдалось.

Для второго примера получим:

5/(1-1) – 3/2 = 15/(1-1) или 5/0 – 3/2 = 15/0

Здесь возникают сомнения: мы встречаемся здесь с делением на нуль, которое невозможно. Если в будущем нам удастся придать определенный, хотя бы и косвенный, смысл этому делению, то тогда мы можем согласиться с тем, что найденное решение x – 1 удовлетворяет нашему уравнению. До этой же поры мы должны признать, что наше уравнение вовсе не имеет решения, имеющего прямой смысл.

Подобные случаи могут иметь место тогда, когда неизвестное входит как-либо в знаменатели дробей, имеющихся в уравнении, причем некоторые из этих знаменателей, при найденном решении, обращаются в нуль.

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

Можно сразу видеть, что данное уравнение имеет форму пропорции: отношение числа x + 3 к числу x – 1 равно отношению числа 2x + 3 к числу 2x – 2. Пусть кто-либо, в виду такого обстоятельства, решит применить сюда для освобождения уравнения от дробей основное свойство пропорции (произведение крайних членов равно произведению средних). Тогда он получит:

(x + 3) (2x – 2) = (2x + 3) (x – 1)

2x 2 + 6x – 2x – 6 = 2x 2 + 3x – 2x – 3.

Здесь может возбудить опасения, что мы не справимся с этим уравнением, то обстоятельство, что в уравнение входят члены с x 2 . Однако, мы можем от обеих частей уравнения вычесть по 2x 2 — от этого уравнение не нарушится; тогда члены с x 2 уничтожатся, и мы получим:

6x – 2x – 6 = 3x – 2x – 3

Перенесем неизвестные члены влево, известные вправо — получим:

Вспоминая данное уравнение

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

мы сейчас же подметим, что найденное значение для x (x = 1) обращает в нуль знаменателей каждой дроби; от такого решения мы, пока не рассмотрели вопроса о делении на нуль, должны отказаться.

Если мы подметим еще, что применение свойства пропорции усложнило дело и что можно было бы получить более простое уравнение, умножая обе части данного на общий знаменатель, а именно на 2(x – 1) — ведь 2x – 2 = 2 (x – 1), то получим:

2(x + 3) = 2x – 3 или 2x + 6 = 2x – 3 или 6 = –3,

Это обстоятельство указывает, что данное уравнение не имеет таких, имеющих прямой смысл решений, которые не обращали бы знаменателей данного уравнения в нуль.
Решим теперь уравнение:

(3x + 5)/(x – 1) = (2x + 18)/(2x – 2)

Умножим обе части уравнения 2(x – 1), т. е. на общий знаменатель, получим:

Найденное решение не обращает в нуль знаменатель и имеет прямой смысл:

или 11 = 11

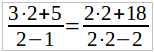
Если бы кто-либо, вместо умножения обеих частей на 2(x – 1), воспользовался бы свойством пропорции, то получил бы:

(3x + 5)(2x – 2) = (2x + 18)(x – 1) или
6x 2 + 4x – 10 = 2x 2 + 16x – 18.

Здесь уже члены с x 2 не уничтожались бы. Перенеся все неизвестные члены в левую часть, а известные в правую, получили бы

Это уравнение мы теперь решить не сумеем. В дальнейшем мы научимся решать такие уравнения и найдем для него два решения: 1) можно взять x = 2 и 2) можно взять x = 1. Легко проверить оба решения:

1) 2 2 – 3 · 2 = –2 и 2) 1 2 – 3 · 1 = –2

Если мы вспомним начальное уравнение

(3x + 5) / (x – 1) = (2x + 18) / (2x – 2),

то увидим, что теперь мы получим оба его решения: 1) x = 2 есть то решение, которое имеет прямой смысл и не обращает знаменателя в нуль, 2) x = 1 есть то решение, которое обращает знаменателя в нуль и не имеет прямого смысла.

Найдем общего знаменателя дробей, входящих в это уравнение, для чего разложим на множители каждого из знаменателей:

1) x 2 – 5x + 6 = x 2 – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),

2) x 2 – x – 2 = x 2 – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),

3) x 2 – 2x – 3 = x 2 – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).

Общий знаменатель равен (x – 3)(x – 2)(x + 1).

Умножим обе части данного уравнения (а его мы теперь можем переписать в виде:

на общего знаменателя (x – 3) (x – 2) (x + 1). Тогда, после сокращения каждой дроби получим:

3(x + 1) – 2(x – 3) = 2(x – 2) или
3x + 3 – 2x + 6 = 2x – 4.

Это решение имеет прямой смысл: оно не обращает в нуль ни одного из знаменателей.

Если бы мы взяли уравнение:

то, поступая совершенно так же, как выше, получили бы

3(x + 1) – 2(x – 3) = x – 2

3x + 3 – 2x + 6 = x – 2

3x – 2x – x = –3 – 6 – 2,

откуда получили бы

что невозможно. Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.

Обобщающий урок по теме «Решение комбинированных уравнений» 11 класс.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Решение комбинированных уравнений.doc

Гадзова Эмма Шадиновна,

учитель математики МОУ «СОШ № 1»

с. Малка Зольского района КБР

Решение сложных комбинированных уравнений

Тип урока: семинарское занятие.

закрепить навыки решения сложных уравнений различными методами.

I Организационный момент:

а) готовность класса к уроку;

б) сообщение цели и задач урока.

ІI Актуализация опорных знаний со слабыми и средними учащимися, работа наиболее подготовленных учащихся по индивидуальным карточкам.

Дать определение уравнения и его корня, равносильности двух уравнений.

Арифметическое выражение, содержащее неизвестную переменную и знаки равенства называют уравнением. Значение переменной, превращающее уравнение в верное равенство, называют корнем уравнения. Два уравнения называют равносильными, если любой корень первого уравнения является корнем второго уравнения и любой корень второго уравнения является корнем первого уравнения.

Дать определение равносильности преобразования уравнения и перечислить основные равносильные преобразования.

Замену одного уравнения другим, равносильным ему уравнением называют равносильным преобразованием уравнения.

Равносильными преобразованиями уравнения являются:

перенос члена уравнения с противоположным знаком из одной части уравнения в другую;

умножение (деление) обеих частей уравнения на отличную от нуля число;

возведение уравнения в нечетную степень;

извлечение корня нечетной степени с обеих частей уравнения:

логарифмирование показательного уравнения;

применение тождеств, т. е равенств, справедливых для любого числа.

Рассказать, какие равносильные преобразования нужно выполнить, чтобы решить следующие уравнения:

;

Дайте определение уравнения – следствия и перечислите преобразования, приводящие к уравнению следствия.

Пусть даны два уравнения. Если любой корень первого уравнения является корнем второго уравнения, то второе уравнение называют уравнением- следствием первого.

Замену уравнения другим уравнением, которое является его следствием, называют переходом к уравнению- следствию.

При переходе к уравнению- следствия возможно появление лишних корней, посторонних для исходного уравнения, поэтому проверка полученных корней является обязательной частью решения уравнения.

Преобразованиями, приводящими к уравнению- следствия является:

возведение уравнения в четную степень;

потенцирование логарифмического уравнения;

освобождение уравнения от знаменателя;

приведение подобных членов;

применение формул (тригонометрических, логарифмических и других).

Расскажите, каким способом приводится следующие уравнения к уравнению — следствия:

;

Сложные уравнения можно решить, приводя их к системам. Правила перехода от уравнений к равносильным системам:

М-область существования

10.

11.

Запишите системы, равносильные уравнениям:

4 .

10.

11.

Решение уравнений с применением формул.

Каким способом можно решить данное уравнение:

Очень часто можно встретить уравнение, которое имеет дополнительное условие, например:

Как можно упростить решение такого типа уравнения?

Учитывая, что левая часть уравнения неотрицательное число получаем значит, множество решений данного уравнения есть . Левая часть уравнения для любого есть отрицательное число, значит, рассматривается только одно уравнение . Решается квадратное уравнение, находим и выбираем те, которые принадлежат множеству М.

Самыми сложными считаются уравнения с параметром. Дайте определение уравнения с параметром. Давайте рассмотрим несколько таких уравнений с использованием свойств функций:

а)

имеет ровно три корня.

Для каждого значения a рассмотрим функцию

Она определена на множестве R , четная, поэтому, если — корень уравнения, то — тоже является корнем уравнения.

Уравнение (1) имеет три корня тогда и только тогда, когда оно имеет и еще два отличных от нуля корня, отличающихся знаками.

получаем:

При уравнение примет вид у уравнения только один корень.

При уравнение имеет вид . Это уравнение имеет три корня Ответ:3

б) Найти все значения параметра а, при которых уравнение

. (2)

имеет ровно четыре корня.

Для каждого значения a рассмотрим функцию

Она определена на множестве R , четная.

Уравнение (2) имеет четыре корня, если уравнение имеет ровно два положительных корня, т.к. корнями уравнения (2) будут . Значит дискриминант уравнения (3) должны быть положительными: