Дифференциальные уравнения первого порядка
Далее в тексте – функции своих аргументов. Штрих ′ означает производную по аргументу. – постоянные.
Дифференциальные уравнения первого порядка, разрешенные относительно производной
Как решать дифференциальные уравнения первого порядка
Пусть мы имеем дифференциальное уравнение первого порядка, разрешенное относительно производной:
.
Разделив это уравнение на , при , мы получим уравнение вида:
,
где .
Далее смотрим, не относятся ли эти уравнения к одному из перечисленных ниже типов. Если нет, то перепишем уравнение в форме дифференциалов. Для этого пишем и умножаем уравнение на . Получаем уравнение в форме дифференциалов:
.
Если это уравнение не является уравнением в полных дифференциалах, то считаем, что в этом уравнении – независимая переменная, а – это функция от . Разделим уравнение на :
.
Далее смотрим, не относится ли это уравнение к одному из, перечисленных ниже типов учитывая, что и поменялись местами.
Если и для этого уравнения не найден тип, то смотрим, нельзя ли упростить уравнение простой подстановкой. Например, если уравнение имеет вид:
,
то замечаем, что . Тогда делаем подстановку . После этого уравнение примет более простой вид:
.
Если и это не помогает, то пытаемся найти интегрирующий множитель ⇓.
Уравнения с разделяющимися переменными
Уравнения, приводящиеся к уравнениям с разделяющимися переменными
Делаем подстановку . Тогда
;
.
Далее разделяем переменные и интегрируем.
Подробнее >>>
Однородные уравнения
Решаем подстановкой:
,
где – функция от . Тогда
;
.
Разделяем переменные и интегрируем.
Подробнее >>>
Уравнения, приводящиеся к однородным
Вводим переменные и :
;
.
Постоянные и выбираем так, чтобы свободные члены обратились в нуль:
;
.
В результате получаем однородное уравнение в переменных и .
Подробнее >>>
Обобщенные однородные уравнения
Делаем подстановку . Получаем однородное уравнение в переменных и .
Подробнее >>>
Линейные дифференциальные уравнения
Есть три метода решения линейных уравнений.
1) Метод интегрирующего множителя.
Умножаем уравнение на интегрирующий множитель :
;
.
Далее интегрируем.
Подробнее >>>
2) Метод Бернулли.
Ищем решение в виде произведения двух функций и от переменной :
.
;
.
Одну из этих функций мы можем выбрать произвольным образом. Поэтому в качестве выбираем любое не нулевое решение уравнения:
.
Определив , получаем уравнение с разделяющимися переменными для .
Подробнее >>>
3) Метод вариации постоянной (Лагранжа).
Здесь мы сначала решаем однородное уравнение:
Общее решение однородного уравнения имеет вид:
,
где – постоянная. Далее мы заменяем постоянную на функцию , зависящую от переменной :
.
Подставляем в исходное уравнение. В результате получаем уравнение, из которого определяем .
Подробнее >>>
Уравнения Бернулли
Подстановкой уравнение Бернулли приводится к линейному уравнению.
Также это уравнение можно решать методом Бернулли. То есть ищем решение в виде произведения двух функций, зависящих от переменной :
.
Подставляем в исходное уравнение:
;
.
В качестве выбираем любое не нулевое решение уравнения:
.
Определив , получаем уравнение с разделяющимися переменными для .
Уравнения Риккати
Оно не решается в общем виде. Подстановкой
уравнение Риккати приводится к виду:
,
где – постоянная; ; .
Далее, подстановкой:
оно приводится к виду:
,
где .
Свойства уравнения Риккати и некоторые частные случаи его решения представлены на странице
Дифференциальное уравнение Риккати >>>
Уравнения Якоби
Уравнения в полных дифференциалах
При условии
.
При выполнении этого условия, выражение в левой части равенства является дифференциалом некоторой функции:
.
Тогда
.
Отсюда получаем интеграл дифференциального уравнения:
.
Для нахождения функции , наиболее удобным способом является метод последовательного выделения дифференциала. Для этого используют формулы:
;
;
;
.
Подробнее >>>
Интегрирующий множитель
Если дифференциальное уравнение первого порядка не приводится ни к одному из перечисленных типов, то можно попытаться найти интегрирующий множитель . Интегрирующий множитель – это такая функция , при умножении на которую, дифференциальное уравнение становится уравнением в полных дифференциалах. Дифференциальное уравнение первого порядка имеет бесконечное число интегрирующих множителей. Однако, общих методов для нахождения интегрирующего множителя нет.
Подробнее >>>
Уравнения, не решенные относительно производной y’
Уравнения, допускающие решение относительно производной y’
Сначала нужно попытаться разрешить уравнение относительно производной . Если это возможно, то уравнение может быть приведено к одному из перечисленных выше типов.
Уравнения, допускающие разложение на множители
Если удастся уравнение разложить на множители:
,
то задача сводится к последовательному решению более простых уравнений:
;
;
;
Подробнее >>>
Уравнения, не содержащие x и y
Уравнения, не содержащие x или y
или
Ищем решение в параметрическом виде. Вводим параметр . Полагаем . Тогда
или .
Далее интегрируем уравнение:
;
.
В результате получаем выражение второй переменной через параметр .
Более общие уравнения:
или
также решаются в параметрическом виде. Для этого нужно подобрать такую функцию , чтобы из исходного уравнения можно было выразить или через параметр .
Чтобы выразить вторую переменную через параметр , интегрируем уравнение:
;
.
Подробнее >>>
Уравнения, разрешенные относительно y
Уравнения Клеро
Такое уравнение имеет общее решение
Подробнее >>>
Уравнения Лагранжа
Решение ищем в параметрическом виде. Полагаем , где – параметр.
Подробнее >>>
Уравнения, приводящиеся к уравнению Бернулли
Эти уравнения приводятся к уравнению Бернулли, если искать их решения в параметрическом виде, введя параметр и делая подстановку .
Подробнее >>>
Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов . Опубликовано: 20-05-2016
Дифференциальные уравнения 1-го порядка,
не разрешенные относительно производной
Уравнения 1-го порядка n-ой степени относительно производной
Пусть имеем дифференциальное уравнение
Решаем это уравнение относительно . Пусть
— вещественные решения уравнения (1).
Общий интеграл уравнения (1) выразится совокупностью интегралов:
где есть интеграл уравнения .
Таким образом, через каждую точку области, в которой принимает вещественные значения, проходит интегральных линий.
Пример 1. Решить уравнение .
Решение. Разрешим это уравнение относительно :
Пример 2. Решить уравнение .
Решение. Разрешим уравнение относительно переменной :
Положим , где — параметр; тогда получим Дифференцируя, найдем . Но так как , то будем иметь
Рассмотрим два случая:
1) , откуда , где — произвольная постоянная. Подставляя значение , получаем общее решение данного уравнения:
В равенстве нельзя заменить на и интегрировать полученное уравнение (так как при этом появится вторая произвольная постоянная, чего не может быть, поскольку рассматриваемое дифференциальное уравнение является уравнением первого порядка).
2) , откуда . Подставляя, получим еще одно решение .
Проверим, нарушится ли свойство единственности в каждой точке решения , т.е. является ли оно особым (см. часть 1.11). Для этого возьмем на интегральной кривой произвольную точку , где . Будем теперь искать решение, которое содержится в общем решении и график которого проходит через точку . Подставляя координаты этой точки в общее решение , будем иметь
откуда . Это значение постоянной подставим в . Тогда получим частное решение
которое не совпадает с решением . Для этих решений имеем соответственно . При обе производные совпадают. Следовательно, в точке нарушается свойство единственности, т. е. через эту точку проходят две интегральные кривые с одной и той же касательной. Так как произвольно, то единственность нарушается в каждой точке решения , а это означает, что оно является особым.
2°. Уравнения вида f(y,y’)=0 и f(x,y’)=0
Если уравнения и легко разрешимы относительно , то, разрешая их, получим уравнения с разделяющимися переменными. Рассмотрим случаи, когда эти уравнения не разрешимы относительно .
А. Уравнение вида разрешимо относительно :
Полагаем , тогда . Дифференцируя это уравнение и заменяя на , получим
Получаем общее решение уравнения в параметрической форме
Пример 3. Решить уравнение , где — постоянные.
Решение. Положим , тогда , или . Отсюда и .
Общим решением будет .
Б. Если уравнение вида неразрешимо (или трудно разрешимо) как относительно , так и относительно , но допускает выражение и через некоторый параметр :
то поступаем следующим образом. Имеем . С другой стороны, , так что и ; отсюда
Таким образом, получаем общее решение данного дифференциального уравнения в параметрической форме
Пример 4. Решить уравнение .
Решение. Полагаем , тогда имеем
Отсюда , общее решение .
В. Уравнение вида . Пусть это уравнение разрешимо относительно , то есть .
Полагая , получим . Но и, следовательно, , так что
Таким образом — общее решение уравнения в параметрической форме ( — параметр).
Замечание. В формулах нельзя рассматривать как производную. В них является просто параметром.
Пример 5. Решить уравнение .
Решение. Положим , тогда
Итак, — общее решение.
Аналогично случаю Б можно пытаться решать уравнение методом введения параметра .
3°. Уравнения Лагранжа
Уравнение Лагранжа имеет вид
Полагая , дифференцируя по и заменяя на , приводим это уравнение к линейному относительно как функции . Находя решение этого последнего уравнения , получаем общее решение исходного уравнения в параметрической форме:
Кроме того, уравнение Лагранжа может иметь еще особые решения вида , где — корень уравнения .
Пример 6. Проинтегрировать уравнение .
Решение. Полагаем , тогда . Дифференцируя, находим
Получили уравнение первого порядка, линейное относительно ; решая его, находим
Подставляя найденное значение в выражение для , получим окончательно
Уравнения Клеро
Уравнение Клеро имеет вид .
Метод решения тот же, что и для уравнения Лагранжа. Общее решение уравнения Клеро имеет вид
Уравнение Клеро может иметь еще особое решение, которое получается исключением из уравнений .
Пример 7. Проинтегрировать уравнение .
Решение. Полагая , получаем . Дифференцируя последнее уравнение и заменяя на , найдем
Приравнивая нулю первый множитель, получаем , откуда и общее решение исходного уравнения есть , однопараметрическое семейство прямых. Приравнивая нулю второй множитель, будем иметь . Исключая из этого уравнения и из уравнения , получим — это тоже решение нашего уравнения (особое решение).
С геометрической точки зрения кривая есть огибающая семейства прямых, даваемых общим решением (рис. 14).
Математика. Шпоры. Решение оду. Постановка задачи Коши для оду 1ого порядка разрешенных и неразрешенных относительно производной для норм систем оду и т д
| Название | Решение оду. Постановка задачи Коши для оду 1ого порядка разрешенных и неразрешенных относительно производной для норм систем оду и т д |
| Анкор | Математика. Шпоры.doc |
| Дата | 24.12.2017 |
| Размер | 0.93 Mb. |
| Формат файла |  |
| Имя файла | Математика. Шпоры.doc |
| Тип | Решение #12746 |
| Категория | Математика |
| страница | 1 из 4 |
Подборка по базе: Практическое занятие 6 РЕШЕНИЕ.docx, Задачи по римскому праву с решением.doc, 4 задачи.docx, Практические (ситуационные ) задачи.doc, Итоговое задание решение.docx, Ситуационные задачи хирургия.docx, Ишемический инсульт Неврология задачи.docx, Психология Задачи к семинарам.doc, 15 урок Решение задач.pptx, Вопросы и задачи УЧР 2021 год.odt
Решением ОДУ называется функция y(x), имеющая непрерывные производные нужного порядка, исходя из уравнений, при постановке которые уравнение превращается в точку. Решением дифференциального уравнения порядка n называется функция y(x) , имеющая на некотором интервале (a, b) производные y ‘( x ), y »( x ). y ( n ) ( x ) до порядка n включительно и удовлетворяющая этому уравнению. Частное решение диф.ур.-ф-ция превращающая ур.в подмножество. Общее решение-все множество частных результатов. Задача Коши-нахождение решения ДУ, удовлетворяющего начальным условиям. ОДУ первого порядка, разрешённое относительно производной Система n ОДУ первого порядка, разрешённая относительно производных (нормальная система n-го порядка) ОДУ n-го порядка, разрешённое относительно старшей производной | Общий вид ОДУ без выделения вектора произвольных постоянных C таков (см. п. 1.1.2):
Если (1) можно разрешить относительно старших производных, т. е. привести к виду
то путем увеличения числа неизвестных скалярных функций (см. п. 1.4.5) уравнение (2) всегда можно привести к нормальному виду
Поэтому в дальнейшем основным объектом изучения будет именно нормальная система (НС). Задача Коши, или начальная задача для уравнения (2) — это система, состоящая из (2) и начального условия
где t0 О R — начальный момент, y0 — начальное значение. Для (НС) начальное условие записывается в виде
Геометрический смысл задачи Коши (НС), (НУ) заключается в том, чтобы во множестве всех интегральных кривых системы (НС) найти ту, которая проходит через точку(t0, x0) (см. рис. 1). График решения ОДУ y=f(x) называется интегральной кривой ДУ. Нахождение множества решений ДУ называют интегрированием ДУ | ||||||
| 2)Уравнения с разделяющимися переменными. 1. Уравнения с разделёнными переменными. Так называются уравнения вида удовлетворяющее начальному условию
Пусть y(x) — решение этого уравнения, т.е. f(x)dx + g(y(x))dy(x) = 0. Интегрируя это тождество, получим 2. Так называются уравнения вида
Эти уравнения легко сводятся к уравнению с разделёнными переменными: Записываем уравнение (1) в форме Уравнение (2) делим на f2(x) g1(y): Эти уравнения — с разделёнными переменными. Интегрируя, получим общие интегралы:
В обоих случаях возможна потеря решений: деление на функцию может привести к уравнению, которое неэквивалентно данному. y = y3, …, очевидно, являются решениями исходного уравнения. В обоих случаях эти решения могут содержаться в общем решении, но могут и не содержаться в нём; последнее может случиться, если на этих решениях нарушаются условия теоремы существования и единственности решения задачи Коши. | 7)ОДУ высших порядков. Простейшие случаи, допускающие понижение порядка уравнения.. Дифференциальным уравнением порядка n называется уравнение вида: В некоторых случаях это уравнение можно разрешить относительно y ( n ) : Так же как и уравнение первого порядка, уравнения высших порядков имеют бесконечное количество решений. Уравнения, допускающие понижение порядка. Понижение порядка диф ур-ния – основной метод решения ур-ний высших порядков. Этот метод дает возможность сравнительно легко находить решение, однако, он применим далеко не ко всем ур-ниям. Рассмотрим случаи, когда возможно понижение порядка. Если f(x) – ф-ция непрерывная на некотором промежутке a 3.Линейное однородное уравнение первого порядка Общее решение: Линейное неоднородное уравнение первого порядка Метод Лагранжа (метод вариации произвольных постоянных)Постановка задачи. Найти решение задачи Коши для линейного неоднородного уравнения с постоянными коэффициентами
1. Записываем соответствующее однородное уравнение с постоянными коэффициентами
Находим фундаментальную систему решений и и общее решение однородного уравнения
2. Применяем метод Лагранжа (метод вариации произвольных постоянных). Если известна фундаментальная система решений и однородного уравнения (3), то общее решение соответствующего неоднородного уравнения (1) может быть найдено по формуле
где функции и определяются из системы линейных алгебраических уравнений |  (4) (4)Интегрируя, находим функции и и записываем общее решение неоднородного уравнения. 3. Используя начальные условия (2), находим решение задачи Коши Метод Бернулли. Одним из методов решения дифференциального уравнения Бернулли является сведение его к линейному неоднородному дифференциальному уравнению первого порядка введением новой переменной . Действительно, при такой замене имеем
После решения этого уравнения и проведения обратной замены получаем искомое решение. | |||||
| 4.Структура решения линейного неоднородного ОДУ. Теорема (о структуре общего решения неоднородного дифференциального уравнения). Общее решение неоднородного дифференциального уравнения есть сумма какого-либо его частного решения и общего решения соответствующего ему однородного уравнения: где – частное решение ДУ(1), y 0 – общее решение соответствующего однородного ДУ (2): y ( n ) + a 1 y ( n -1) + . +a n y = 0, Докажем теорему для уравнения второго порядка y // + py / + qy = f ( x ). (4) Рассмотрим соответствующее однородное ДУ: y // + py / + q = 0. (5) Обозначим y 1, y 2 его линейно независимые частные решения и y 0 = c 1 y 1 + c 2 y 2 – его общее решение.) Пусть – какое-то частное решение ДУ (4). Покажем, что решение (3) удовлетворяет ДУ (4). Подставим формулу (3) в ДУ (4) (предва-рительно найдём производные): Получаем тождественное равенство, так как первая скобка обращается в нуль в силу того, что y 0– общее решение однородного ДУ(5), а вторая скобка равна правой части, так как – частное решение ДУ (4). Теорема доказана. то |  5)Уравнение Бернулли, два метода его решения 5)Уравнение Бернулли, два метода его решенияЕсли α — действительное число, отличающееся от 0 и 1, т.к. при α=0 и α=1 ур-ние обращается в линейное. Данное ур-ние решается 2 способами: 1.Из него можно сделать линейное ур-ние, разделив : 2..Решать точно так же как и однородное ур-ние, поскольку левая часть у них одинаковая. | ||||||
| 6.Рассмотрим уравнение вида F ( x , y , y ‘ ) = 0 , не разрешённое относительно производной. Если попытаться выразить из него y ‘ , то можно получить , вообще говоря , несколько уравнений источники: http://mathhelpplanet.com/static.php?p=differentsialnye-uravneniya-pervogo-poryadka—ne-razreshennye-otnositelno-proizvodnoi http://topuch.ru/reshenie-odu-postanovka-zadachi-koshi-dlya-odu-1ogo-poryadka-r/index.html |
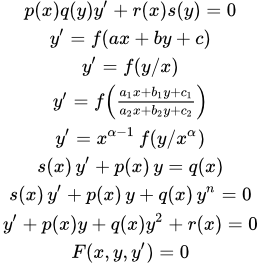








 — общий интеграл (общее решение) этого уравнения.
— общий интеграл (общее решение) этого уравнения.  Исходное уравнение — с разделёнными переменными, интегрируя его, получим
Исходное уравнение — с разделёнными переменными, интегрируя его, получим  . Соотношение (x-1) 2 + y 3 = C — общее решение (общий интеграл) уравнения; для того, чтобы найти частное решение, удовлетворяющее начальному условию, надо подставить в общее решения данные значения x0 и y0, и найти значение постоянной C на этом решении: (2-1) 2 + 1 3 = 2
. Соотношение (x-1) 2 + y 3 = C — общее решение (общий интеграл) уравнения; для того, чтобы найти частное решение, удовлетворяющее начальному условию, надо подставить в общее решения данные значения x0 и y0, и найти значение постоянной C на этом решении: (2-1) 2 + 1 3 = 2  C = 2. Таким образом, решение поставленной задачи: (x-1) 2 + y 3 = 2.
C = 2. Таким образом, решение поставленной задачи: (x-1) 2 + y 3 = 2. или (1)
или (1) , затем делим на g(y) и умножаем на dx:
, затем делим на g(y) и умножаем на dx:  .
. .
. .
. .
. .
. .
.


 .
.




 (1)
(1) . (2)
. (2) . (3)
. (3) .
. ,
, . При n = 1 это дифференциальное уравнение становится уравнением с разделяющимися переменными
. При n = 1 это дифференциальное уравнение становится уравнением с разделяющимися переменными  .
. и дифференциальное уравнение Бернулли примет вид
и дифференциальное уравнение Бернулли примет вид .
.





 — решение уравнения
— решение уравнения













