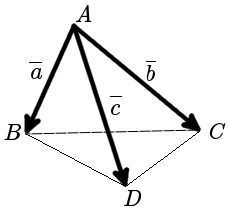
Смешанное произведение векторов.
Формулы вычисления смешанного произведения векторов
Смешанное произведение векторов равно определителю матрицы, составленной из этих векторов.
Смешанное произведение векторов a = < ax ; ay ; az >, b = < bx ; by ; bz > и c = < cx ; cy ; cz > в декартовой системе координат можно вычислить, используя следующую формулу:
| a · [ b × c ] = | ax | ay | az |
| bx | by | bz | |
| cx | cy | cz |
Свойства смешанного произведения векторов
| Vпир = | 1 | | a · [ b × c ]| |
| 6 |
Примеры задач на вычисления смешанного произведения векторов
| a · [ b × с ] = | 1 | 2 | 3 | = |
| 1 | 1 | 1 | ||
| 1 | 2 | 1 |
= 1·1·1 + 1·1·2 + 1·2·3 — 1·1·3 — 1·1·2 — 1·1·2 = 1 + 2 + 6 — 3 — 2 — 2 = 2
Решение: Найдем смешанное произведение этих векторов:
| a · [ b × с ] = | 1 | 2 | 3 | = |
| 1 | -1 | 1 | ||
| 2 | 0 | -1 |
= 1·(-1)·(-1) + 2·1·2 + 3·1·0 — 3·(-1)·2 — 2·1·(-1) — 1·1·0 =
= 1 + 4 + 0 + 6 + 2 — 0 = 13
Найдем объем пирамиды воспользовавшись свойствами:
| Vпир = | 1 | | a · [ b × c ]| = | 13 | = 2 | 1 |
| 6 | 6 | 6 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Смешанное произведение векторов. Онлайн калькулятор
Данный онлайн калькулятор вычисляет смешанное произведение векторов. Дается подробное решение. Для вычисления смешанного произведения векторов выберите способ представления векторов (по координатам или по двум точкам) введите данные в ячейки и нажимайте на кнопку «Вычислить.»
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Смешанное произведение векторов (теория)
Смешанное произведение трех векторов это число, которое получается при скалярном произведении результата векторного произведения первых двух векторов на третьий вектор. Другими словами, если заданы три вектора a, b и c, то для получения смешанного произведения этих векторов, сначала векторно умножаются первые два вектора и полученный вектор [ab] скалярно умножается на вектор c.
Смешанное произведение трех векторов a, b и c обозначается так: abc или так (a,b,c). Тогда можно записать:
Прежде чем сформулировать теорему, представляющую геометрический смысл смешанного произведения, ознакомьтесь с понятиями правая тройка, левая тройка, правая система координат, левая система координат (определения 2, 2′ и 3 на странице векторное произведение векторов онлайн).
Для определенности, в дальнейшем мы будем рассматривать только правые системы координат.
Теорема 1. Смешанное произведение векторов ([ab],c) равно объему параллелипеда, построенного на приведенных к общему началу векторах a, b, c, взятому со знаком плюс, если тройка a, b, c правая, и со знаком минус, если тройка a, b, c левая. Если векторы a, b, c компланарны, то ([ab],c) равно нулю.
Следствие 1. Имеет место следующее равенство:
Для доказательства следствия заметим, что из переместительного свойства скалярного произведения имеем:
Следовательно нам достаточно доказать, что
Из выражения (3) видно, что левая и правая часть равны объему параллелипеда. Но и знаки правой и левой частей совпадают, так как тройки векторов abc и bca имеют одинаковую ориентацию.
Доказанное равенство (1) позволяет записать смешанное произведение трех векторов a, b, c просто в виде abc, не указывая, какие именно два вектора перемножаются векторно первые два или последние два.
Следствие 2. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.
Доказательство вытекает из теоремы 1. Действительно, если векторы компланарны, то смешанное произведение этих векторов равно нулю. Обратное, если смешанное произведение равно нулю, то из теоремы 1 вытекает компланарность этих векторов (так как объем параллелипеда, построенного на приведенных к общему началу векторах равно нулю).
Следствие 3. Смешанное произведение трех векторов, два из которых совпадают, равно нулю.
Действительно. Если два вектора из трех совпадают, то они компланарны. Следовательно, смешанное произведение этих векторов равно нулю.
Смешанное произведение векторов в декартовых координатах
Теорема 2. Пусть три вектора a, b и c определены своими декартовыми прямоугольными координатами
| a=<x1, y1, z1>, b=<x2, y2, z2>, c=<x3, y3, z3>. |
Тогда смешанное произведение abc равняется определителю, строки которого соответственно равны координатам перемножаемых векторов:
 . . | (4) |
Доказательство. Смешанное произведение abc равно скалярному произведению векторов [ab] и c. Векторное произведение векторов [ab] в декартовых координатах вычисляется формулой (подробнее смотрите на странице векторное произведение векторов онлайн):
| [ab]=<y1z2—y2z1, z1x2−z2x1, x1y2−x2y1>. |
Тогда скалярное произведение векторов [ab] и c можно записать так:
| abc=([ab],c)=x3(y1z2—y2z1)+ y3(z1x2−z2x1)+ z3(x1y2−x2y1). | (5) |
Последнее выражение можно записать, используя определители второго порядка:
  . . | (6) |
Формулы (6) и (4) эквивалентны, так как (6) является разложением определителя (4) по третьей строке.
Следствие 3. Для компланарности трех векторов
| a=<x1, y1, z1>, b=<x2, y2, z2>, c=<x3, y3, z3>. |
необходимо и достаточно равенство нулю определителя, строки которой заполнены координатами этих векторов, т.е:
 . . | (7) |
Для доказательства следствия достаточно рассмотреть формулу (4) и следствие 2.
Смешанное произведение векторов на примерах
Пример 1. Найти смешанное произведение векторов abс, где
 , ,  , ,  . . |
Для вычисления смешанного произведения векторов a, b, c составим матрицу, строки которой образуются векторами a, b, c:
 . . |
Смешанное произведение векторов a, b, c равен определителю матрицы L. Вычислим определитель матрицы L, разложив определитель по строке 1:
   . . |
Смешанное произведение векторов a, b, c равен :
Пример 2. Найти смешанное произведение векторов abс, где
Начальная точка вектора a:
 . . |
Конечная точка вектора a:
 . . |
 . . |
Начальная точка вектора c:
 . . |
Конечная точка вектора c:
 . . |
Переместим вектор a на начало координат. Для этого вычтем из соответствующих координат конечной точки B координаты начальной точки A:
 . . |
Переместим вектор c на начало координат. Для этого вычтем из соответствующих координат конечной точки F координаты начальной точки E:
 . . |
Для вычисления смешанного произведения векторов a, b, c составим матрицу, строки которой образуются векторами a, b, c:
 . . |
Смешанное произведение векторов a, b, c равен определителю матрицы L. Вычислим определитель матрицы L, разложив определитель по строке 1:
    . . |
Смешанное произведение векторов a, b, c равен :
Смешанное произведение векторов, его свойства, примеры и решения
Для того, чтобы подробно рассмотреть такую тему, нужно охватить еще несколько разделов. Тема напрямую связана с такими терминами, как скалярное и векторное произведение. В этой статье мы постарались дать точное определение, указать формулу, которая поможет определить произведение, используя координаты векторов. Помимо этого, статья включает в себя разделы с перечислением свойств произведения и представлены подробный разбор типовых равенств и задач.
Термин
Для того, чтобы определить, в чем заключается данный термин, нужно взять три вектора.
Смешанным произведением a → , b → и d → является та величина, которая равняется скалярному произведению a → × b → и d → , где a → × b → — умножение a → и b → . Операцию умножения a → , b → и d → зачастую обозначают a → · b → · d → . Можно преобразовать формулу так: a → · b → · d → = ( a → × b → , d → ) .
Умножение в системе координат
Мы можем умножить вектора, если они указаны на координатной плоскости.
Возьмем i → , j → , k →
Произведение векторов в данном конкретном случае будет иметь следующий вид: a → × b → = ( a y · b z — a z · b y ) · i → + ( a z · b x + a x · b z ) · j → + ( a x · b y + a y · b x ) · k → = a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k →
Для выполнения скалярного произведения в системе координат необходимо сложить результаты, полученный во время умножения координат.
Из этого следует:
a → × b → = ( a y · b z — a z · b y ) · i → + ( a z · b x + a x · b z ) · j → + ( a x · b y + a y · b x ) · k → = a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k →
Мы также можем определить смешанное произведение векторов, если в заданной системе координат указаны координаты векторов, которые умножаются.
a → × b → = ( a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k → , d x · i → + d y · j → + d z · k → ) = = a y a z b y b z · d x — a x a z b x b z · d y + a x a y b x b y · d z = a x a y a z b x b y b z d x d y d z
Таким образом, можно сделать вывод, что:
a → · b → · d = a → × b → , d → = a x a y a z b x b y b z d x d y d z
Смешанное произведение можно приравнять к определителю матрицы, в качестве строк которой использованы векторные координаты. Наглядно это выглядит так: a → · b → · d = a → × b → , d → = a x a y a z b x b y b z d x d y d z .
Свойства операции над векторами Из особенностей, которые выделяются в скалярном или векторном произведении, можно вывести особенности, которые характеризуют смешанное произведение. Ниже мы приведем основные свойства.
- ( λ · a → ) · b → · d → = a → · ( λ · b → ) · d → = a → · b → · ( λ · d → ) = λ · a → · b → · d → λ ∈ R ;
- a → · b → · d → = d → · a → · b → = b → · d → · a → ; a → · d → · b → = b → · a → · d → = d → · b → · a → ;
- ( a ( 1 ) → + a ( 2 ) → ) · b → · d → = a ( 1 ) → · b → · d → + a ( 2 ) → · b → · d → a → · ( b ( 1 ) → + b ( 2 ) → ) · d → = a → · b ( 1 ) → · d → + a → · b ( 2 ) → · d → a → · b → · ( d ( 1 ) → + d ( 2 ) → ) = a → · b → · d ( 2 ) → + a → · b → · d ( 2 ) →
Помимо приведенных свойств, следует уточнить, что если множитель нулевой, то результатом умножения также станет нуль.
Результатом умножения также будет нуль в том случае, если два или больше множителей равны.
Действительно, если a → = b → , то, следуя определению векторного произведения [ a → × b → ] = a → · b → · sin 0 = 0 , следовательно, смешанное произведение равно нулю, так как ( [ a → × b → ] , d → ) = ( 0 → , d → ) = 0 .
Если же a → = b → или b → = d → , то угол между векторами [ a → × b → ] и d → равен π 2 . По определению скалярного произведения векторов ( [ a → × b → ] , d → ) = [ a → × b → ] · d → · cos π 2 = 0 .
Свойства операции умножения чаще всего требуются во время решения задач.
Для того, чтобы подробно разобрать данную тему, возьмем несколько примеров и подробно их распишем.
Докажите равенство ( [ a → × b → ] , d → + λ · a → + b → ) = ( [ a → × b → ] , d → ) , где λ — некоторое действительное число.
Для того, чтобы найти решение этого равенства, следует преобразовать его левую часть. Для этого необходимо воспользоваться третьим свойством смешанного произведения, которое гласит:
( [ a → × b → ] , d → + λ · a → + b → ) = ( [ a → × b → ] , d → ) + ( [ a → × b → ] , λ · a → ) + ( [ a → × b → ] , b → )
Мы разобрали, что ( ( [ a → × b → ] , b → ) = 0 . Из этого следует, что
( [ a → × b → ] , d → + λ · a → + b → ) = ( [ a → × b → ] , d → ) + ( [ a → × b → ] , λ · a → ) + ( [ a → × b → ] , b → ) = = ( [ a → × b → ] , d → ) + ( [ a → × b → ] , λ · a → ) + 0 = ( [ a → × b → ] , d → ) + ( [ a → × b → ] , λ · a → )
Согласно первому свойству ( [ a ⇀ × b ⇀ ] , λ · a → ) = λ · ( [ a ⇀ × b ⇀ ] , a → ) , а ( [ a ⇀ × b ⇀ ] , a → ) = 0 . Таким образом, ( [ a ⇀ × b ⇀ ] , λ · a → ) . Поэтому,
( [ a ⇀ × b ⇀ ] , d → + λ · a → + b → ) = ( [ a ⇀ × b ⇀ ] , d → ) + ( [ a ⇀ × b ⇀ ] , λ · a → ) = = ( [ a ⇀ × b ⇀ ] , d → ) + 0 = ( [ a ⇀ × b ⇀ ] , d → )
Необходимо доказать, что модуль смешанного произведения трех векторов не больше, чем произведения их длин.
Решение
Исходя из условия, можно представить пример в виде неравенства a → × b → , d → ≤ a → · b → · d → .
По определению, преобразуем неравенство a → × b → , d → = a → × b → · d → · cos ( a → × b → ^ , d → ) = = a → · b → · sin ( a → , b → ^ ) · d → · cos ( [ a → × b → ^ ] , d )
Используя элементарные функции, можно сделать вывод, что 0 ≤ sin ( a → , b → ^ ) ≤ 1 , 0 ≤ cos ( [ a → × b → ^ ] , d → ) ≤ 1 .
Из этого можно сделать вывод, что
( a → × b → , d → ) = a → · b → · sin ( a → , b → ) ^ · d → · cos ( a → × b → ^ , d → ) ≤ ≤ a → · b → · 1 · d → · 1 = a → · b → · d →
Разбор типовых задач
Для того, чтобы определить, чему равно произведение векторов, следует знать координаты умножаемых векторов. Для операции можно использовать такую формулу a → · b → · d → = ( a → × b → , d → ) = a x a y a z b x b y b z d x d y d z .
В прямоугольной системе координат представлены 3 вектора с такими координатами: a → = ( 1 , — 2 , 3 ) , b → ( — 2 , 2 , 1 ) , d → = ( 3 , — 2 , 5 ) . Необходимо определить, чему равно произведение указанных векторов a → · b → · d → .
Исходя из теории, представленной выше, мы можем воспользоваться правилом, которое гласит, что смешанное произведение может быть вычислено через определитель матрицы. Это будет выглядеть так: a → · b → · d → = ( a → × b → , d → ) = a x a y a z b x b y b z d x d y d z = 1 — 2 3 — 2 2 1 3 — 2 5 = = 1 · 2 · 5 + ( — 1 ) · 1 · 3 + 3 · ( — 2 ) · ( — 2 ) — 3 · 2 · 3 — ( — 1 ) · ( — 2 ) · 5 — 1 · 1 · ( — 2 ) = — 7
Необходимо найти произведение векторов i → + j → , i → + j → — k → , i → + j → + 2 · k → , где i → , j → , k → — орты прямоугольной декартовой системы координат.
Исходя из условия, которое гласит, что вектора расположены в данной системе координат, можно вывести их координаты: i → + j → = ( 1 , 1 , 0 ) i → + j → — k → = ( 1 , 1 , — 1 ) i → + j → + 2 · k → = ( 1 , 1 , 2 )
Используем формулу, которая использовалась выше
i → + j → × ( i → + j → — k → , ( i → + j → + 2 · k → ) = 1 1 0 1 1 — 1 1 1 2 = 0 i → + j → × ( i → + j → — k → , ( i → + j → + 2 · k → ) = 0
Смешанное произведение также возможно определить с помощью длины вектора, которая уже известна, и угла между ними. Разберем этот тезис в примере.
В прямоугольной системе координат расположены три вектора a → , b → и d → , которые перпендикулярны между собой. Они представляют собой правую тройку, их длины составляют 4 , 2 и 3 . Необходимо умножить вектора.
Обозначим c → = a → × b → .
Согласно правилу, результатом умножения скалярных векторов является число, которое равно результату умножения длин используемых векторов на косинус угла между ними. Делаем вывод, что a → · b → · d → = ( [ a → × b → ] , d → ) = c → , d → = c → · d → · cos ( c → , d → ^ ) .
Используем длину вектора d → , указанную в условии примера: a → · b → · d → = c → · d → · cos ( c → , d → ^ ) = 3 · c → · cos ( c → , d → ^ ) . Необходимо определить с → и с → , d → ^ . По условию a → , b → ^ = π 2 , a → = 4 , b → = 2 . Вектор c → найдем с помощью формулы: c → = [ a → × b → ] = a → · b → · sin a → , b → ^ = 4 · 2 · sin π 2 = 8
Можно сделать вывод, что c → перпендикулярен a → и b → . Вектора a → , b → , c → будут являться правой тройкой, так использована декартовая система координат. Векторы c → и d → будут однонаправленными, то есть, c → , d → ^ = 0 . Используя выведенные результаты, решаем пример a → · b → · d → = 3 · c → · cos ( c → , d → ^ ) = 3 · 8 · cos 0 = 24 .
Геометрический смысл
Используем множители a → , b → и d → .
Вектора a → , b → и d → исходят от одной точки. Используем их как стороны для построения фигуры.
Обозначим, что c → = [ a → × b → ] . Для данного случая можно определить произведение векторов как a → · b → · d → = c → · d → · cos ( c → , d → ^ ) = c → · n p c → d → , где n p c → d → — числовая проекция вектора d → на направление вектора c → = [ a → × b → ] .
Абсолютная величина n p c → d → равняется числу, которое также является равно высоте фигуры, для которого использованы вектора a → , b → и d → в качестве сторон. Исходя из этого, следует уточнить, что c → = [ a → × b → ] перпендикулярен a → и вектору и вектору согласно определению умножения векторов. Величина c → = a → x b → равняется площади параллелепипеда, построенного на векторах a → и b → .
Делаем вывод, что модуль произведения a → · b → · d → = c → · n p c → d → равен результату умножения площади основания на высоту фигуры, которая построена на векторах a → , b → и d → .
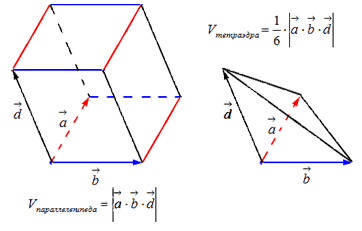
Абсолютная величина векторного произведения является объемом параллелепипеда: V п а р а л л е л е п и п и д а = a → · b → · d → .
Данная формула и является геометрическим смыслом.
Объем тетраэдра, который построен на a → , b → и d → , равняется 1 / 6 объема параллелепипеда Получаем, V т э т р а э д а = 1 6 · V п а р а л л е л е п и п и д а = 1 6 · a → · b → · d → .
Для того, чтобы закрепить знания, разберем несколько типичных примеров
Необходимо найти объем параллелепипеда, в качестве сторон которого используются A B → = ( 3 , 6 , 3 ) , A C → = ( 1 , 3 , — 2 ) , A A 1 → = ( 2 , 2 , 2 ) , заданные в прямоугольной системе координат. Объем параллелепипеда можно найти, используя формулу об абсолютной величине. Из этого следует: A B → · A C → · A A 1 → = 3 6 3 1 3 — 2 2 2 2 = 3 · 3 · 2 + 6 · ( — 2 ) · 2 + 3 · 1 · 2 — 3 · 3 · 2 — 6 · 1 · 2 — 3 · ( — 2 ) · 2 = — 18
Тогда, V п а р а л л е л е п и п е д а = — 18 = 18 .
V п а р а л л е л е п и п и д а = 18
В системе координат заданы точки A ( 0 , 1 , 0 ) , B ( 3 , — 1 , 5 ) , C ( 1 , 0 , 3 ) , D ( — 2 , 3 , 1 ) . Следует определить объем тетраэдра, который расположен на этих точках.
Воспользуемся формулой V т э т р а э д р а = 1 6 · A B → · A C → · A D → . Мы можем определить координаты векторов по координатам точек: A B → = ( 3 — 0 , — 1 — 1 , 5 — 0 ) = ( 3 , — 2 , 5 ) A C → = ( 1 — 0 , 0 — 1 , 3 — 0 ) = ( 1 , — 1 , 3 ) A D → = ( — 2 — 0 , 3 — 1 , 1 — 0 ) = ( — 2 , 2 , 1 )
Дальше определяем смешанное произведение A B → · A C → · A D → по координатам векторов: A B → · A C → · A D → = 3 — 2 5 1 — 1 3 — 2 2 1 = 3 · ( — 1 ) · 1 + ( — 2 ) · 3 · ( — 2 ) + 5 · 1 · 2 — 5 · ( — 1 ) · ( — 2 ) — ( — 2 ) · 1 · 1 — 3 · 3 · 2 = — 7 Объем V т э т р а э д р а = 1 6 · — 7 = 7 6 .
http://matworld.ru/vector/smeshannoe-proizvedenie-online.php
http://zaochnik.com/spravochnik/matematika/vektory/smeshannoe-proizvedenie-vektorov/