Смешанные задачи на уравнение прямой и плоскости

Основные задачи о прямых и плоскостях

Уравнение прямой, проходящей через две точки.

Пусть в пространстве задана общая декартова система координат и две точки \(M_<1>\) и \(M_<2>\) с координатами \((x_<1>, y_<1>, z_<1>)\) и \((x_<2>, y_<2>, z_<2>)\). Чтобы написать уравнение прямой \(M_<1>M_<2>\), примем \(M_<1>\) за начальную точку, a \(\overrightarrowM_<2>>\) за направляющий вектор. Этот вектор не нулевой, если точки не совпадают. По формуле уравнения прямой в пространстве мы получаем
$$
\frac>-x_<1>>=\frac>-y_<1>>=\frac>-z_<1>>.\label
$$
Если в этих равенствах какой-либо из знаменателей равен нулю, то следует приравнять нулю соответствующий числитель.

В планиметрии задача решается также. Отличие только в том, что координаты точек теперь \((x_<1>, y_<1>)\) и \((x_<2>, y_<2>)\), и мы получаем по формуле для прямой на плоскости
$$
\begin
x-x_<1>& y-y_<1>\\
x_<2>-x_<1>& y_<2>-y_<1>
\end
= 0.\nonumber
$$

Уравнение плоскости, проходящей через три точки.

Пусть \(M_<1>\), \(M_<2>\) и \(M_<3>\) — не лежащие на одной прямой точки с координатами \((x_<1>, y_<1>, z_<1>)\), \((x_<2>, y_<2>, z_<2>)\) и \((x_<3>, y_<3>, z_<3>)\) в общей декартовой системе координат. Выберем \(M_<1>\) в качестве начальной точки, a \(\overrightarrowM_<2>>\) и \(\overrightarrowM_<3>>\) в качестве направляющих векторов. Тогда по формуле о компланарности прямой и плоскости и формуле для выражения смешанного произведения через координаты получаем уравнение плоскости
$$
\begin
x-x_<1>& y-y_<1>& z-z_<1>\\
x_<2>-x_<1>& y_<2>-y_<1>& z_<2>-z_<1>\\
x_<3>-x_<1>& y_<3>-y_<1>& z_<3>-z_<1>
\end
= 0.\label
$$

Параллельность прямой и плоскости.

Легко проверить, что все приведенные здесь условия являются не только необходимыми, но и достаточными.

Из формулы \eqref следует, что три плоскости пересекаются в одной точке тогда и только тогда, когда коэффициенты их уравнений удовлетворяют условию
$$
\begin
A& B& C\\
A_<1>& B_<1>& C_<1>\\
A_<2>& B_<2>& C_<2>
\end
\neq 0.\label
$$
Действительно, это неравенство означает, что прямая, по которой пересекаются две плоскости, не параллельна третьей.

Полупространство.

Пусть даны плоскость \(P\) и определенный ее нормальный вектор \(\boldsymbol\). Полупространством, определяемым \(P\) и \(\boldsymbol\), называется множество точек \(M\) таких, что для некоторой точки \(M_<0>\) на плоскости вектор \(\overrightarrowM>\) составляет с \(\boldsymbol\) угол, не больший \(\pi/2\).

Если \(\boldsymbol\) — радиус-вектор точки \(M\), а \(\boldsymbol_<0>\) — точки \(M_<0>\), то определение полупространства, эквивалентно неравенству \((\boldsymbol-\boldsymbol_<0>, \boldsymbol) \geq 0\). Это неравенство и есть уравнение полупространства.

Мы получим уравнение полупространства в координатной форме, если вспомним, что согласно утверждению 3 отсюда выражение \((\boldsymbol-\boldsymbol_<0>, \boldsymbol)\) в координатах записывается линейным многочленом \(Ax+By+Cz+D\). Итак, полупространство в декартовой системе координат задается линейным неравенством
$$
Ax+By+Cz+D \geq 0.\nonumber
$$
Обратно, любое такое неравенство можно записать как \((\boldsymbol-\boldsymbol_<0>, \boldsymbol) \geq 0\), откуда сразу видно, что оно задает полупространство.

Плоскость \(P\) и вектор \(\boldsymbol_ <1>=-\boldsymbol\) задают другое полупространство с уравнением \((\boldsymbol-\boldsymbol_<0>, \boldsymbol_<1>) \geq 0\) или \((\boldsymbol-\boldsymbol_<0>, \boldsymbol) \leq 0\). Его назовем “отрицательным”, в отличие от “положительного” полупространства \((\boldsymbol-\boldsymbol_<0>, \boldsymbol) \geq 0\). Однако такое наименование условно — оно определяется выбором вектора \(\boldsymbol\). Изменение направления этого вектора равносильно умножению уравнения плоскости на (—1). При этом “положительное” полупространство становится “отрицательным”, и наоборот.

Вот, однако, факт, не зависящий от выбора направления нормального вектора: если \(M_<1>(x_<1>, y_<1>, z_<1>)\) и \(M_<2>(x_<2>, y_<2>, z_<2>)\) две точки, не лежащие в плоскости, то результаты подстановки их координат в левую часть уравнения плоскости \(Ax_<1>+By_<1>+Cz_<1>+D\) и \(Ax_<2>+By_<2>+Cz_<2>+D\) имеют один знак тогда и только тогда, когда точки лежат в одном полупространстве.

Для решения задач бывает полезно следующее замечание: если точка \(M_<0>(x_<0>, y_<0>, z_<0>)\) лежит на плоскости, то точка с координатами \(x_<0>+A\), \(y_<0>+B\), \(z_<0>+C\) лежит в “положительном” полупространстве. Иначе говоря, вектор с координатами \(A, B, C\) направлен в “положительное” полупространство. Это легко проверяется подстановкой.

Вполне аналогично сказанному о полупространствах мы можем определить, что такое полуплоскость, и доказать, что неравенство \(Ax+By+Cz+D \geq 0\), связывающее декартовы координаты точки на плоскости, определяет полуплоскость. Вторая полуплоскость, ограниченная прямой \(Ax+By+C=0\), задается неравенством \(Ax+By+C \leq 0\).

Точки \(M_<1>(x_<1>, y_<1>)\) и \(M_<2>(x_<2>, y_<2>)\) лежат по одну сторону от прямой тогда и только тогда, когда \((Ax_<1>+By_<1>+C)(Ax_<2>+By_<2>+C) > 0\).

Расстояние от точки до плоскости.

Пусть дана плоскость с уравнением \((\boldsymbol-\boldsymbol_<0>, \boldsymbol)=0\) и точка \(M\) с радиус-вектором \(R\). Рассмотрим вектор \(\overrightarrowM>=\boldsymbol-\boldsymbol_<0>\), соединяющий начальную точку плоскости с \(M\) (рис. 7.1). Расстояние от точки до плоскости равно модулю его скалярной проекции на вектор \(\boldsymbol\), то есть
$$
h=\frac<|(\boldsymbol-\boldsymbol_<0>, \boldsymbol)|><|\boldsymbol|>.\label
$$

Если в декартовой прямоугольной системе координат точка \(M\) имеет координаты \((X, Y, Z)\), то равенство \eqref запишется согласно ранее доказанным утверждениям (здесь и здесь) так:
$$
h=\frac<|AX+BY+CZ+D|><\sqrt+B^<2>+C^<2>>>.\label
$$

Рис. 7.1. Расстояние от точки до плоскости.

Расстояние от точки до прямой.

Рис. 7.2. Расстояние от точки до прямой.

Рассмотрим прямую на плоскости, заданную уравнением \(Ax+By+C=0\) в декартовой прямоугольной системе координат. Пусть \(M_<0>(x_<0>, y_<0>)\) — начальная точка прямой, a \(M(X, Y)\) — некоторая точка плоскости. В качестве направляющего вектора возьмем вектор \(\boldsymbol(-B, A)\). Мы знаем (ранее доказывали), что площадь параллелограмма равна \(S=|(X-x_<0>)A-(Y-y_<0>)(-B)|\). Тогда по формуле \(S=|AX+BY+C|\) и
$$
h=\frac<|AX+BY+C|><\sqrt+B^<2>>>.\label
$$

Легко заметить также, что для нахождения расстояния от точки до прямой на плоскости можно воспользоваться формулой \eqref, считая, что \(\boldsymbol\) — нормальный вектор прямой.

Расстояние между скрещивающимися прямыми.

Рис. 7.3. Расстояние между скрещивающимися прямыми

Вычисление углов.

Чтобы найти угол между двумя прямыми, следует найти их направляющие векторы и вычислить косинус угла между ними, используя скалярное произведение. При этом следует иметь в виду, что, изменив направление одного из векторов, мы получим косинус смежного угла.

Для нахождения угла между прямой и плоскостью определяют угол \(\theta\) между направляющим вектором прямой и нормальным вектором плоскости. Если векторы выбрать так, чтобы \(\cos \theta \geq 0\), и взять \(0 \leq \theta \leq \pi/2\), то искомый угол дополняет \(\theta\) до \(\pi/2\).

Угол между плоскостями находят как угол между их нормальными векторами.

Полезна бывает формула для угла между прямыми линиями на плоскости, заданными уравнениями \(y=k_<1>x+b_<1>\) и \(y=k_<2>x+b_<2>\) декартовой прямоугольной системе координат. Обозначим через \(\varphi\) угол между прямыми, отсчитываемый от первой прямой ко второй в том же направлении, в котором производится кратчайший поворот от первого базисного вектора ко второму. Тогда \(\operatorname \varphi\) можно найти как тангенс разности углов, которые прямые составляют с осью абсцисс. Так как тангенсы этих углов равны угловым коэффициентам прямых, мы получаем
$$
\operatorname \varphi=\frac-k_<1>><1+k_<1>k_<2>>.\label
$$

Рис. 7.4. \(\varphi=\varphi_<2>-\varphi_<2>\)

Конечно, эта формула не имеет смысла, когда знаменатель дроби обращается в нуль. В этом случае прямые перпендикулярны. Действительно, векторы с компонентами \(1, k_<1>\) и \(1, k_<2>\) — направляющие векторы прямых, и их скалярное произведение равно \(1+k_<1>k_<2>\). Таким образом, верно следующее утверждение.

Для перпендикулярности прямых с угловыми коэффициентами \(k_<1>\) и \(k_<2>\) в декартовой прямоугольной системе координат необходимо и достаточно выполнение равенства \(1+k_<1>k_<2>=0\).

Некоторые задачи на построение.

Перпендикуляр из точки на плоскость. Проекция точки.

Если \((\boldsymbol-\boldsymbol_<0>, \boldsymbol)=0\) — уравнение плоскости и дана точка \(M\) с радиус-вектором \(\boldsymbol\), то прямая с уравнением \(\boldsymbol=\boldsymbol+t\boldsymbol\) проходит через \(M\) и перпендикулярна плоскости. Решая совместно уравнения прямой и плоскости, найдем ортогональную проекцию \(M\) на плоскость. Из \((\boldsymbol-\boldsymbol_<0>+t\boldsymbol, \boldsymbol)\) находим \(t\) и подставляем в уравнение прямой. Мы получим радиус-вектор проекции
$$
\boldsymbol_<1>=\boldsymbol-\frac<(\boldsymbol-\boldsymbol_<0>, \boldsymbol)><|\boldsymbol|^<2>>\boldsymbol.\nonumber
$$
Таким образом, из радиус-вектоpa \(\boldsymbol\) вычитается проекция \(\boldsymbol-\boldsymbol_<0>\) на нормальный вектор плоскости.

Перпендикуляр из точки на прямую.

Уравнение проекции прямой на плоскость.

Общий перпендикуляр к двум скрещивающимся прямым.

Рис. 7.5. Перпендикуляр между скрещивающимися прямыми

Пучок прямых.

Пучком прямых на плоскости называется множество прямых, проходящих через фиксированную точку — центр пучка. Пусть \(A_<1>x+B_<1>y+C_<1>=0\) и \(A_<2>x+B_<2>y+C_<2>=0\) — уравнения двух прямых, принадлежащих пучку. Тогда уравнение
$$
\alpha(A_<1>x+B_<1>y+C_<1>)+\beta(A_<2>x+B_<2>y+C_<2>)=0\label
$$
при условии \(\alpha^<2>+\beta^ <2>\neq 0\) называется уравнением пучка прямых.

Основанием для этого служит следующее утверждение.

При любых \(\alpha\) и \(\beta\) \((\alpha^<2>+\beta^ <2>\neq 0)\) уравнение \eqref определяет прямую линию, принадлежащую пучку. Обратно, уравнение каждой прямой из пучка представимо в виде \eqref.

Докажем сначала, что коэффициенты при переменных в уравнении \eqref не равны нулю одновременно. Для этого перепишем его в виде
$$
(\alpha A_<1>+\beta A_<2>)x+(\alpha B_<1>+\beta B_<2>)y+(\alpha C_<1>+\beta C_<2>)=0.\nonumber
$$
Допустим, что \(\alpha A_<1>+\beta A_<2>=0\) и \(\alpha B_<1>+\beta B_<2>=0\). Так как прямые пересекаются, \(A_<1>B_<2>-A_<2>B_ <1>\neq 0\) и из утверждения о существовании решения системы уравнений вытекает, что значения \(\alpha=0\), \(\beta=0\) единственные, которые удовлетворяют этим двум равенствам. Но эти значения мы исключили. Таким образом, уравнение \eqref определяет прямую линию.

Обозначим через \(x_<0>\), \(y_<0>\) координаты центра пучка. По условию
$$
A_<1>x_<0>+B_<1>y_<0>+C_<1>=0,\ A_<2>x_<0>+B_<2>y_<0>+C_<2>=0,\nonumber
$$
а потому \(x_<0>\), \(y_<0>\) удовлетворяют уравнению \eqref, и прямая проходит через центр пучка.

Вторая часть предложения будет доказана, если окажется, что через любую точку, отличную от центра пучка \(M_<0>\), проходит прямая линия с уравнением вида \eqref. Легко проверить, так ли это. Рассмотрим точку \(M_<1>(x_<1>, y_<1>)\), отличную от \(M_<0>\), и обозначим
$$
u=A_<1>x_<1>+B_<1>y_<1>+C_<1>=0,\ v=A_<2>x_<1>+B_<2>y_<1>+C_<2>=0\nonumber
$$
Так как наши прямые имеют только одну общую точку, числа \(u\) и \(v\) одновременно не равны нулю, и мы вправе положить \(\alpha=-v\), \(\beta=-u\). При таких значениях \(\alpha\) и \(\beta\) координаты точки \(M_<1>\) удовлетворяют уравнению \eqref. Это означает, что соответствующая этим значениям прямая пучка проходит через \(M_<1>\), и утверждение доказано.

Заметим, что каждая пара чисел \(\alpha\) и \(\beta\) \((\alpha^<2>+\beta^ <2>\neq 0)\) определяет в пучке единственную прямую, но каждой прямой соответствуют бесконечно много пропорциональных между собой пар чисел.

Если нам известны координаты центра пучка, то уравнение пучка можно написать в виде
$$
\alpha(x-x_<0>)+\beta(y-y_<0>)=0,\nonumber
$$
положив, что пучок определяется прямыми \(x-x_<0>=0\) и \(y-y_<0>=0\). Впрочем, и без того очевидно, что это — уравнение произвольной прямой, проходящей через \(M_<0>\).

Систему из уравнений прямых, определяющих пучок, можно рассматривать как уравнение центра пучка. Поэтому уравнение каждой прямой пучка есть следствие этой системы. Теперь наш результат можно сформулировать так.

Если система линейных уравнений имеет решение., то некоторое линейное уравнение является ее следствием тогда и только тогда, когда оно есть сумма уравнений системы, умноженных на какие-то числа.

Мы доказали это предложение для частного случая систем из двух уравнений с двумя неизвестными. В общем виде оно вытекает из результатов главы о системах линейных уравнений. Другими геометрическими интерпретациями этого предложения являются пучки и связки плоскостей.

Пучком плоскостей называется множество плоскостей, проходящих через фиксированную прямую — ось пучка. Уравнение пучка плоскостей имеет вид
$$
\alpha(A_<1>x+B_<1>y+C_<1>z+D_<1>)+\beta(A_<2>x+B_<2>y+C_<2>z+D_<2>)=0,\nonumber
$$
где \(\alpha^<2>+\beta^ <2>\neq 0\), а в скобках стоят левые части уравнений двух различных плоскостей пучка.

Связкой плоскостей называется множество плоскостей, проходящих через фиксированную точку — центр связки. Уравнение связки плоскостей имеет вид
$$
\alpha(A_<1>x+B_<1>y+C_<1>z+D_<1>)+\beta(A_<2>x+B_<2>y+C_<2>z+D_<2>) +\\+ \gamma(A_<3>x+B_<3>y+C_<3>z+D_<3>)=0,\nonumber
$$
где \(\alpha^<2>+\beta^<2>+\gamma^ <2>\neq 0\), а в скобках стоят левые части уравнений плоскостей связки, имеющих центр своей единственной общей точкой.

О геометрическом смысле порядка алгебраической линии.

Предположим, что на плоскости дана алгебраическая линия \(L\), имеющая в декартовой системе координат уравнение
$$
A_<1>x^>y^>+…+A_x^>y^>=0.\label
$$
Рассмотрим произвольную прямую с параметрическими уравнениями
$$
x=x_<0>+a_<1>t,\ y=y_<0>+a_<2>t.\label
$$
Найдем точки пересечения \(L\) и прямой линии. Они будут известны, если мы найдем соответствующие им значения параметра \(t\). Это будут те значения, при которых \(x\) и \(y\), выраженные по формулам \eqref, удовлетворяют уравнению \eqref. Подставим \eqref в \eqref:
$$
A_<1>(x_<0>+a_<1>t)^>(y_<0>+a_<2>t)^>+…+A_(x_<0>+a_<1>t)^>(y_<0>+a_<2>t)^>=0.\label
$$
Раскрывая скобки в каждом члене, мы получим многочлены относительно \(t\) степеней \(k_<1>+l_<1>, …, k_+l_\). Их сумма будет многочленом, степень которого не выше, чем максимальная из степеней слагаемых. Но максимальное из чисел \(k_<1>+l_<1>,…,k_+l_\) — это порядок линии \(L\). Поэтому степень уравнения \eqref не превосходит порядка линии.

Может, конечно, случиться, что все коэффициенты этого уравнения равны нулю, и оно представляет собой тождество. Если исключить этот случай, то число корней уравнения и, следовательно, число точек пересечения не превосходит порядка линии. Таким образом, мы доказали следующее утверждение.

Число точек пересечения алгебраической линии с прямой, которая на ней не лежит целиком, не превосходит порядка линии.

Существуют линии, которые ни с одной прямой не имеют в принципе возможного числа точек пересечения, равного порядку линии. Примерами могут служить линии с уравнениями \(x^<2>+y^<2>=0\) или \((x^<2>+y^<2>)^<2>-1=0\).

Архимедова спираль — линия с уравнением \(r=\alpha\varphi\) в полярной системе координат — пересекает каждую прямую, проходящую через полюс, в бесконечном числе точек. Следовательно, она не является алгебраической линией.

4.1.8. Примеры решения задач по теме «Уравнение прямой на плоскости»

Даны уравнения двух сторон параллелограмма: 2Х + У + 3 = 0 и 2Х – 5У + 9 = 0 и уравнение одной из его диагоналей: 2Х – у — 3 = 0. Найти координаты вершин этого параллелограмма.

Выясните, уравнения каких сторон даны в условии задачи: параллельных или

Смежных, и как расположена данная диагональ по отношению к данным сторонам.

Выясним, уравнения каких сторон даны в условии задачи: параллельных или

Следовательно, прямые пересекаются, то есть даны уравнения смежных сторон параллелограмма.

Условие параллельности прямых

.

Пусть даны уравнения сторон АВ и AD. Тогда координаты точки А будут решением системы уравнений:

Теперь определим, уравнение какой диагонали: АС или BD – нам известно. Если это диагональ АС, то на ней лежит точка А, следовательно, координаты этой точки должны удовлетворять уравнению диагонали. Проверим:

Значит, точка А не лежит на данной прямой, то есть дано уравнение диагонали BD.

Тогда вершина В лежит на прямых АВ и BD, значит, ее координаты найдем из системы:

Система уравнений для определения координат точки D составлена из уравнений прямых AD И BD:

Остается найти координаты точки С. Составим уравнения прямых ВС и DC.

Поскольку ВС параллельна AD, их угловые коэффициенты равны. Найдем угловой коэффициент прямой AD:

Тогда ВС можно задать уравнением

Найдем координаты точки С, решив систему из двух полученных уравнений:

Найти точку, симметричную точке А(2; 1) относительно прямой, проходящей через точки В(-1; 7) и С(1; 8).

Представьте себе, что вам нужно Построить искомую точку на плоскости. Последовательность действий при этом можно задать так:

1) провести прямую ВС;

2) провести через точку А прямую, перпендикулярную ВС;

3) найти точку О пересечения этих прямых и отложить на прямой АО по другую сторону прямой ВС отрезок ОА1 = АО.

Представим себе, что нам нужно Построить искомую точку на плоскости. Последовательность действий при этом можно задать так:

4) провести прямую ВС;

5) провести через точку А прямую, перпендикулярную ВС;

6) найти точку О пересечения этих прямых и отложить на прямой АО по другую сторону прямой ВС отрезок ОА1 = АО.

Тогда точка А1 будет симметричной точке А относительно прямой ВС.

Теперь заменим каждое из действий составлением уравнений и вычислением координат точек.

1) Найдем уравнение прямой ВС в виде:

2) Найдем угловой коэффициент прямой ВС:

Прямая АО Перпендикулярна прямой ВС, поэтому

Составим уравнение прямой АО:

3) Найдем координаты точки О как решение системы:

4) Точка О – середина отрезка АА1, поэтому

Найти угол между прямыми L1: 3Х – у + 5 = 0 и L2: 2Х + У – 7 = 0.

Если J – угол между прямыми L1 и L2, то J = A2 — A1, где A2 и A1 – углы, образованные прямыми L1 и L2 с положительной полуосью Ох. Тогда

Где K1 и K2 – угловые коэффициенты прямых L1 и L2.

Если J – угол между прямыми L1 и L2, то J = A2 — A1, где A2 и A1 – углы, образованные прямыми L1 и L2 с положительной полуосью Ох. Тогда

Где K1 и K2 – угловые коэффициенты прямых L1 и L2. Найдем K1 и K2: для L1

Y = 3X + 5, K1 = 3; для второй: Y = -2X + 7, K2 = -2. Следовательно,

Для прямых А1х + В1У + С1 = 0 И А2Х + В2У + С2 = 0

.

Определить, лежит ли точка М(2; 3) внутри или вне треугольника, стороны которого заданы уравнениями 4Х – у – 7 = 0, Х + 3У – 31 = 0, Х + 5У – 7 = 0.

Если точка М расположена внутри треугольника АВС, то ее отклонение δ от каждой стороны треугольника имеет тот же знак, что и для вершины, не лежащей на этой стороне, а если точка М лежит вне треугольника, то по крайней мере с одной из вершин она окажется в разных полуплоскостях относительно стороны треугольника.

Пусть первое уравнение задает сторону АВ, второе – ВС, третье – АС. Найдем координаты точек А, В и С:

Для ответа на вопрос задачи отметим, что:

1) если точка М расположена внутри треугольника АВС, то ее отклонение δ от каждой стороны треугольника имеет тот же знак, что и для вершины, не лежащей на этой стороне (т. е. точка М расположена относительно каждой стороны треугольника в одной полуплоскости с третьей вершиной);

2) если точка М лежит вне треугольника, то по крайней мере с одной из вершин она окажется в разных полуплоскостях относительно стороны треугольника (на рисунке: точки М1 и В расположены по разные стороны от прямой АС).

Составим нормальные уравнения сторон треугольника АВС:

Вычислим соответствующие отклонения:

1) для точек М и А относительно прямой ВС:

2) для точек М и В относительно прямой АС:

3) для точек М и С относительно прямой АВ:

Итак, точки М И С лежат по разные стороны от прямой АВ. Следовательно, точка М расположена вне треугольника АВС.

Ответ: Точка М расположена вне треугольника АВС.

Для треугольника АВС с вершинами А(-3; -1), В(1; 5), С(7; 3) составить уравнения медианы и высоты, выходящих из вершины В.

Составьте уравнение медианы как прямой, проходящей через точки В и М – середину стороны АС, а высоты – как прямой, проходящей через точку В и перпендикулярной стороне АС.

1) Медиана ВМ проходит через точку В и точку М – середину отрезка АС. Найдем координаты точки М:

Тогда уравнение медианы можно записать в виде:

2) Высота ВН перпендикулярна стороне АС. Составим уравнение АС:

Ответ: медиана ВМ: 4Х + У – 9 = 0; высота ВН: 5Х + 2У – 15 = 0.

Определить, при каком значении А прямая

Параллельна оси ординат. Написать уравнение прямой.

Если прямая параллельна оси ординат, то в уравнении Ах + Ву + С = 0

Если прямая параллельна оси ординат, то в уравнении Ах + Ву + С = 0

В = 0, С ≠ 0. Из условия В = 0 получаем: А2 – 1 = 0, А = ± 1.

При А = 1 С = 2 + 7 – 9 = 0 – второе условие не выполняется (получившаяся при этом прямая -4Х = 0 не параллельна оси Оу, а совпадает с ней).

При А = -1 получим: -6Х – 14 = 0, 3Х + 7 = 0.

Составить уравнения всех прямых, проходящих через точку М(2; 3) и отсекающих от координатного угла треугольник площадью 12.

Составьте уравнение искомой прямой «в отрезках»:

Где |A| и |B| — длины отрезков, отсекаемых прямой на координатных осях. Тогда

Откуда |Ab| = 24. Кроме того, координаты точки М(2; 3) должны удовлетворять уравнению «в отрезках».

Составим уравнение искомой прямой «в отрезках»:

Где |A| и |B| — длины отрезков, отсекаемых прямой на координатных осях. Тогда

Откуда |Ab| = 24. Кроме того, координаты точки М(2; 3) должны удовлетворять уравнению «в отрезках». Таким образом, для А и B можно составить систему уравнений:

Следовательно, условию задачи удовлетворяют три прямые:

Общее уравнение прямой: описание, примеры, решение задач

Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.

Общее уравнение прямой: основные сведения

Пусть на плоскости задана прямоугольная система координат O x y .

Любое уравнение первой степени, имеющее вид A x + B y + C = 0 , где А , В , С – некоторые действительные числа ( А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид A x + B y + C = 0 при некотором наборе значений А , В , С .

указанная теорема состоит из двух пунктов, докажем каждый из них.

1. Докажем, что уравнение A x + B y + C = 0 определяет на плоскости прямую.

Пусть существует некоторая точка М 0 ( x 0 , y 0 ) , координаты которой отвечают уравнению A x + B y + C = 0 . Таким образом: A x 0 + B y 0 + C = 0 . Вычтем из левой и правой частей уравнений A x + B y + C = 0 левую и правую части уравнения A x 0 + B y 0 + C = 0 , получим новое уравнение, имеющее вид A ( x — x 0 ) + B ( y — y 0 ) = 0 . Оно эквивалентно A x + B y + C = 0 .

Полученное уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 является необходимым и достаточным условием перпендикулярности векторов n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) . Таким образом, множество точек M ( x , y ) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n → = ( A , B ) . Можем предположить, что это не так, но тогда бы векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) не являлись бы перпендикулярными, и равенство A ( x — x 0 ) + B ( y — y 0 ) = 0 не было бы верным.

Следовательно, уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение A x + B y + C = 0 определяет ту же прямую. Так мы доказали первую часть теоремы.

1. Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени A x + B y + C = 0 .

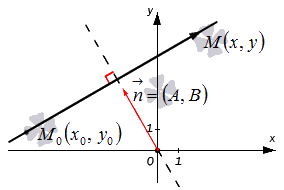
Зададим в прямоугольной системе координат на плоскости прямую a ; точку M 0 ( x 0 , y 0 ) , через которую проходит эта прямая, а также нормальный вектор этой прямой n → = ( A , B ) .

Пусть также существует некоторая точка M ( x , y ) – плавающая точка прямой. В таком случае, векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:

n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) = 0

Перепишем уравнение A x + B y — A x 0 — B y 0 = 0 , определим C : C = — A x 0 — B y 0 и в конечном результате получим уравнение A x + B y + C = 0 .

Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.

Уравнение, имеющее вид A x + B y + C = 0 – это общее уравнение прямой на плоскости в прямоугольной системе координат O x y .

Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.

Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой A x + B y + C = 0 .

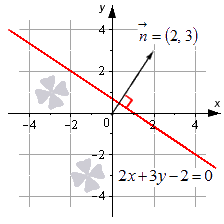
Рассмотрим конкретный пример общего уравнения прямой.

Пусть задано уравнение 2 x + 3 y — 2 = 0 , которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n → = ( 2 , 3 ) . Изобразим заданную прямую линию на чертеже.

Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2 x + 3 y — 2 = 0 , поскольку координаты всех точек заданной прямой отвечают этому уравнению.

Мы можем получить уравнение λ · A x + λ · B y + λ · C = 0 , умножив обе части общего уравнения прямой на число λ , не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.

Неполное уравнение общей прямой

Полное общее уравнение прямой – такое общее уравнение прямой A x + B y + C = 0 , в котором числа А , В , С отличны от нуля. В ином случае уравнение является неполным.

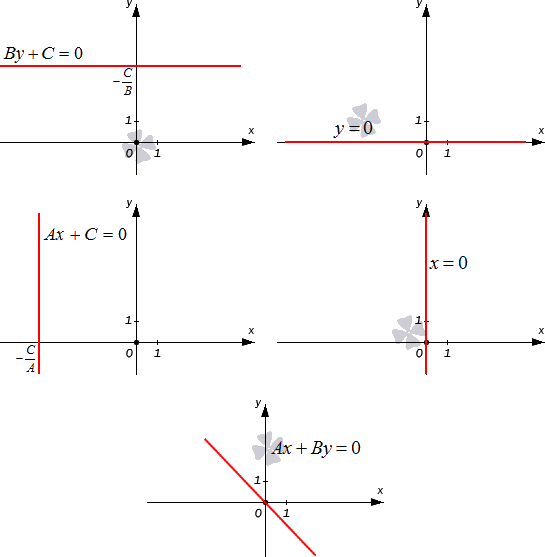
Разберем все вариации неполного общего уравнения прямой.

1. Когда А = 0 , В ≠ 0 , С ≠ 0 , общее уравнение принимает вид B y + C = 0 . Такое неполное общее уравнение задает в прямоугольной системе координат O x y прямую, которая параллельна оси O x , поскольку при любом действительном значении x переменная y примет значение — C B . Иначе говоря, общее уравнение прямой A x + B y + C = 0 , когда А = 0 , В ≠ 0 , задает геометрическое место точек ( x , y ) , координаты которых равны одному и тому же числу — C B .
2. Если А = 0 , В ≠ 0 , С = 0 , общее уравнение принимает вид y = 0 . Такое неполное уравнение определяет ось абсцисс O x .
3. Когда А ≠ 0 , В = 0 , С ≠ 0 , получаем неполное общее уравнение A x + С = 0 , задающее прямую, параллельную оси ординат.
4. Пусть А ≠ 0 , В = 0 , С = 0 , тогда неполное общее уравнение примет вид x = 0 , и это есть уравнение координатной прямой O y .
5. Наконец, при А ≠ 0 , В ≠ 0 , С = 0 , неполное общее уравнение принимает вид A x + B y = 0 . И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел ( 0 , 0 ) отвечает равенству A x + B y = 0 , поскольку А · 0 + В · 0 = 0 .

Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.

Известно, что заданная прямая параллельна оси ординат и проходит через точку 2 7 , — 11 . Необходимо записать общее уравнение заданной прямой.

Решение

Прямая, параллельная оси ординат, задается уравнением вида A x + C = 0 , в котором А ≠ 0 . Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения A x + C = 0 , т.е. верно равенство:

Из него возможно определить C , если придать A какое-то ненулевое значение, к примеру, A = 7 . В таком случае получим: 7 · 2 7 + C = 0 ⇔ C = — 2 . Нам известны оба коэффициента A и C , подставим их в уравнение A x + C = 0 и получим требуемое уравнение прямой: 7 x — 2 = 0

Ответ: 7 x — 2 = 0

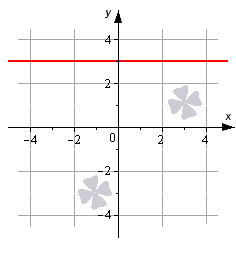
На чертеже изображена прямая, необходимо записать ее уравнение.

Решение

Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси O x и проходит через точку ( 0 , 3 ) .

Прямую, которая параллельна очи абсцисс, определяет неполное общее уравнение B y + С = 0 . Найдем значения B и C . Координаты точки ( 0 , 3 ) , поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой B y + С = 0 , тогда справедливым является равенство: В · 3 + С = 0 . Зададим для В какое-то значение, отличное от нуля. Допустим, В = 1 , в таком случае из равенства В · 3 + С = 0 можем найти С : С = — 3 . Используем известные значения В и С , получаем требуемое уравнение прямой: y — 3 = 0 .

Ответ: y — 3 = 0 .

Общее уравнение прямой, проходящей через заданную точку плоскости

Пусть заданная прямая проходит через точку М 0 ( x 0 , y 0 ) , тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: A x 0 + B y 0 + C = 0 . Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A ( x — x 0 ) + B ( y — y 0 ) + C = 0 , это уравнение эквивалентно исходному общему, проходит через точку М 0 ( x 0 , y 0 ) и имеет нормальный вектор n → = ( A , B ) .

Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.

Даны точка М 0 ( — 3 , 4 ) , через которую проходит прямая, и нормальный вектор этой прямой n → = ( 1 , — 2 ) . Необходимо записать уравнение заданной прямой.

Решение

Исходные условия позволяют нам получить необходимые данные для составления уравнения: А = 1 , В = — 2 , x 0 = — 3 , y 0 = 4 . Тогда:

A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 1 · ( x — ( — 3 ) ) — 2 · y ( y — 4 ) = 0 ⇔ ⇔ x — 2 y + 22 = 0

Задачу можно было решить иначе. Общее уравнение прямой имеет вид A x + B y + C = 0 . Заданный нормальный вектор позволяет получить значения коэффициентов A и B , тогда:

A x + B y + C = 0 ⇔ 1 · x — 2 · y + C = 0 ⇔ x — 2 · y + C = 0

Теперь найдем значение С, используя заданную условием задачи точку М 0 ( — 3 , 4 ) , через которую проходит прямая. Координаты этой точки отвечают уравнению x — 2 · y + C = 0 , т.е. — 3 — 2 · 4 + С = 0 . Отсюда С = 11 . Требуемое уравнение прямой принимает вид: x — 2 · y + 11 = 0 .

Ответ: x — 2 · y + 11 = 0 .

Задана прямая 2 3 x — y — 1 2 = 0 и точка М 0 , лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна — 3 . Необходимо определить ординату заданной точки.

Решение

Зададим обозначение координат точки М 0 как x 0 и y 0 . В исходных данных указано, что x 0 = — 3 . Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:

2 3 x 0 — y 0 — 1 2 = 0

Определяем y 0 : 2 3 · ( — 3 ) — y 0 — 1 2 = 0 ⇔ — 5 2 — y 0 = 0 ⇔ y 0 = — 5 2

Ответ: — 5 2

Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно

Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.

Для начала рассмотрим переход от общего уравнения вида A x + B y + C = 0 к каноническому уравнению x — x 1 a x = y — y 1 a y .

Если А ≠ 0 , тогда переносим слагаемое B y в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: A x + C A = — B y .

Это равенство возможно записать как пропорцию: x + C A — B = y A .

В случае, если В ≠ 0 , оставляем в левой части общегь уравнения только слагаемое A x , прочие переносим в правую часть, получаем: A x = — B y — C . Выносим – В за скобки, тогда: A x = — B y + C B .

Перепишем равенство в виде пропорции: x — B = y + C B A .

Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.

Задано общее уравнение прямой 3 y — 4 = 0 . Необходимо преобразовать его в каноническое уравнение.

Решение

Запишем исходное уравнение как 3 y — 4 = 0 . Далее действуем по алгоритму: в левой части остаётся слагаемое 0 x ; а в правой части выносим — 3 за скобки; получаем: 0 x = — 3 y — 4 3 .

Запишем полученное равенство как пропорцию: x — 3 = y — 4 3 0 . Так, мы получили уравнение канонического вида.

Ответ: x — 3 = y — 4 3 0 .

Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.

Прямая задана уравнением 2 x — 5 y — 1 = 0 . Запишите параметрические уравнения этой прямой.

Решение

Осуществим переход от общего уравнения к каноническому:

2 x — 5 y — 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2

Теперь примем обе части полученного канонического уравнения равными λ , тогда:

x 5 = λ y + 1 5 2 = λ ⇔ x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R

Ответ: x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R

Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y = k · x + b , но только тогда, когда В ≠ 0 . Для перехода в левой части оставляем слагаемое B y , остальные переносятся в правую. Получим: B y = — A x — C . Разделим обе части полученного равенство на B , отличное от нуля: y = — A B x — C B .

Задано общее уравнение прямой: 2 x + 7 y = 0 . Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.

Решение

Произведем нужные действия по алгоритму:

2 x + 7 y = 0 ⇔ 7 y — 2 x ⇔ y = — 2 7 x

Ответ: y = — 2 7 x .

Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида x a + y b = 1 . Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на – С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y :

A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1

Необходимо преобразовать общее уравнение прямой x — 7 y + 1 2 = 0 в уравнение прямой в отрезках.

Решение

Перенесем 1 2 в правую часть: x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .

Разделим на -1/2 обе части равенства: x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .

Преобразуем далее в необходимый вид: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .

Ответ: x — 1 2 + y 1 14 = 1 .

В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.

Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:

x a + y b ⇔ 1 a x + 1 b y — 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y — k x — b = 0 ⇔ A x + B y + C = 0

Каноническое уравнение преобразуется к общему по следующей схеме:

x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x ( y — y 1 ) ⇔ ⇔ a y x — a x y — a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0

Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ A x + B y + C = 0

Заданы параметрические уравнения прямой x = — 1 + 2 · λ y = 4 . Необходимо записать общее уравнение этой прямой.

Решение

Осуществим переход от параметрических уравнений к каноническому:

x = — 1 + 2 · λ y = 4 ⇔ x = — 1 + 2 · λ y = 4 + 0 · λ ⇔ λ = x + 1 2 λ = y — 4 0 ⇔ x + 1 2 = y — 4 0

Перейдем от канонического к общему:

x + 1 2 = y — 4 0 ⇔ 0 · ( x + 1 ) = 2 ( y — 4 ) ⇔ y — 4 = 0

Ответ: y — 4 = 0

Задано уравнение прямой в отрезках x 3 + y 1 2 = 1 . Необходимо осуществить переход к общему виду уравнения.

Решение:

Просто перепишем уравнение в необходимом виде:

x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y — 1 = 0

Ответ: 1 3 x + 2 y — 1 = 0 .

Составление общего уравнения прямой

Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A ( x — x 0 ) + B ( y — y 0 ) = 0 . Там же мы разобрали соответствующий пример.

Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.

Задана прямая, параллельная прямой 2 x — 3 y + 3 3 = 0 . Также известна точка M 0 ( 4 , 1 ) , через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.

Решение

Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n → = ( 2 , — 3 ) : 2 x — 3 y + 3 3 = 0 . Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:

A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 2 ( x — 4 ) — 3 ( y — 1 ) = 0 ⇔ 2 x — 3 y — 5 = 0

Ответ: 2 x — 3 y — 5 = 0 .

Заданная прямая проходит через начало координат перпендикулярно прямой x — 2 3 = y + 4 5 . Необходимо составить общее уравнение заданной прямой.

Решение

Нормальный вектором заданной прямой будет направляющий вектор прямой x — 2 3 = y + 4 5 .

Тогда n → = ( 3 , 5 ) . Прямая проходит через начало координат, т.е. через точку О ( 0 , 0 ) . Составим общее уравнение заданной прямой:

A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 3 ( x — 0 ) + 5 ( y — 0 ) = 0 ⇔ 3 x + 5 y = 0