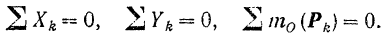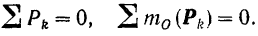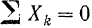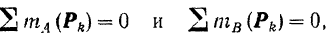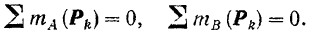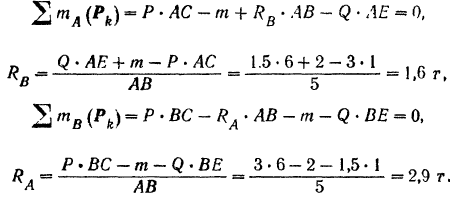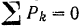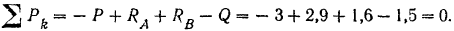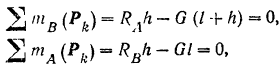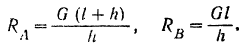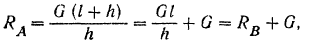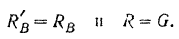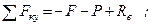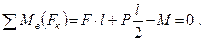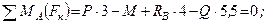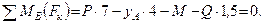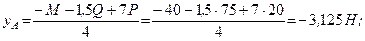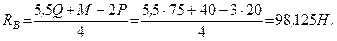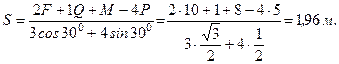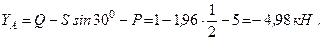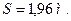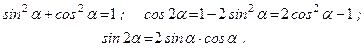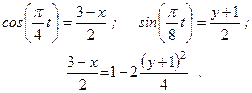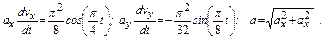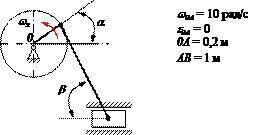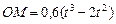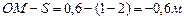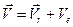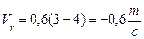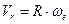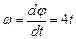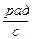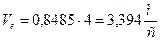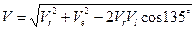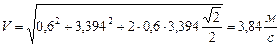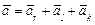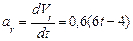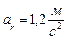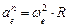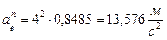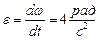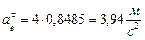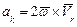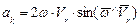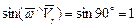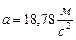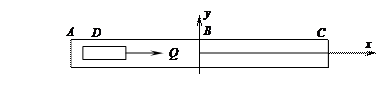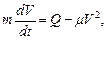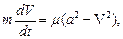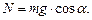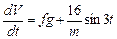Уравнения равновесия плоской системы параллельных сил
Уравнения равновесия плоской системы параллельных сил
Так как параллельное расположение сил на плоскости является частным случаем их произвольного на ней расположения, то к такой системе также могут быть применены установленные в предыдущем параграфе три уравнения равновесия плоской системы сил:
Пользуясь тем, что оси проекций можно располагать в плоскости действия сил как угодно, проведем ось 
Проекция каждой из сил на ось 
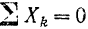
Так как все данные силы параллельны оси 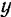
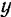
Для простоты будем в дальнейшем обозначать эту сумму просто
Таким образом, уравнения равновесия для плоской системы параллельных сил принимают вид
Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы порознь равнялись нулю алгебраическая сумма всех сил и сумма алгебраических величин моментов всех сил относительно любой точки, лежащей в плоскости действия сил.
Вспоминая сказанное на стр. 83 о третьей возможной форме уравнении равновесия плоской системы сил (уравнения (28)), уравнениям равновесия плоской системы параллельных сил можно придать другую форму.
Направим ось 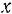
обращается о тождество и отпадает.
Остаются два уравнения
причем центры 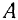
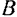
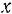
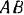
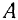
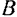
Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы порознь равнялись нулю суммы алгебраических величин моментов всех сил относительно каждой из двух произвольно выбранных, но не лежащих на прямой, параллельной данным силам, точек плоскости:
Пример задачи:
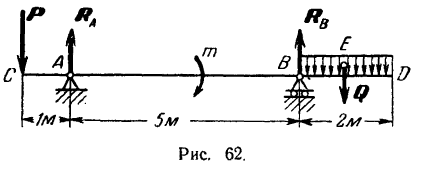
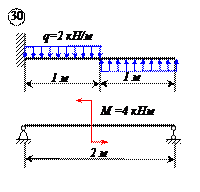
На двухконсольную горизонтальную балку действует пара сил с моментом 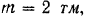
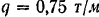
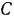
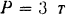
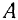
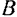
Решение:
Для определения реакций опор заменим распределенную нагрузку, действующую на участке балки длиной 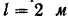
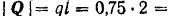
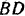
Реакция 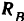
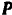
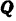
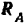
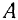
Составляем уравнения (30) равновесия балки. Так как (стр. 74) сумма алгебраических величии моментов сил пары относительно любого центра равна моменту пары и данная пара вращает плоскость чертежа по часовой стрелке, то
Полученный результат можно проверить. Так как балка находится в равновесии, то уравнение
должно обращаться при подстановке в него значений приложенных к балке сил в тождество. Действительно,
Силы пары в это уравнение мы не подставляем, так как алгебраическая сумма их всегда равна нулю.
Пример задачи:
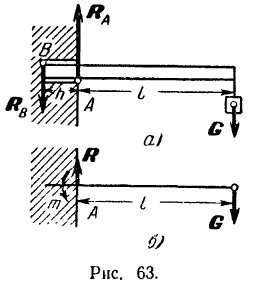
Балка заложена в стену на глубину 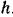
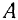
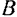
Решение:
Как видно из рис. 63, а, приложенная к балке сила 
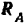
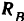
Составляя уравнения (30) равновесия для плоской системы параллельных сил, будем иметь:
Найденным реакциям стены в месте заделки можно придать и другую (рис. 63,6), часто применяемую форму, о которой было сказано выше (стр. 85). Так как
то реакцию 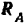
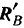
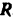
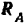
Силы 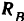
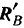
Этот момент, как видно из уравнения (II), равен но абсолютной величине моменту активной силы 
Он уравновешивает вращательный эффект приложенной к балке активной силы, т. е. препятствует вращению балки. Как видно из предыдущего равенства 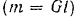
Реакция 
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Возможно вам будут полезны эти дополнительные темы:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
iSopromat.ru
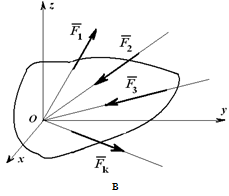
Рассмотрим условия равновесия произвольной плоской и пространственной систем сил, включая три основные формы и частные случаи равновесия для систем параллельных и сходящихся сил:
Из основной теоремы статики следует, что любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом.
Если система уравновешена, то получаем условия равновесия: R=0, MO=0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:
Формы условий равновесия
Первая форма
Для плоской системы сил (например, в плоскости Oxy) из этих уравнений получаются только три:
причем оси и точка O, относительно которой пишется уравнение моментов, выбираются произвольно. Это первая форма уравнений равновесия.
Вторая форма
Уравнения равновесия могут быть записаны иначе:
Это вторая форма уравнений равновесия, причем ось Ox не должна быть перпендикулярна линии, проходящей через точки A и B.
Третья форма
Это третья форма уравнений равновесия, причем точки A, B и C не должны лежать на одной прямой.
Предпочтительность написания форм уравнений равновесия зависит от конкретных условий задачи и навыков решающего.
Другие условия равновесия
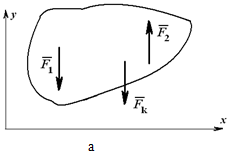
При действии на тело плоской системы параллельных сил одно из уравнений исчезает и остаются два уравнения (рисунок 1.26, а):
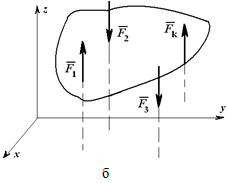
Для пространственной системы параллельных сил (рисунок 1.26, б) могут быть записаны три уравнения равновесия:
Для системы сходящихся сил (линии действия которых пересекаются в одной точке) можно написать три уравнения для пространственной системы:
и два уравнения для плоской системы:
В каждом из вышеприведенных случаев число неизвестных, находимых при решении уравнений, соответствует числу записанных уравнений равновесия.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ СИЛ
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Практикум
Для студентов факультета заочного обучения
Составители: А.С. ЗАЙЦЕВ
Редактор А.Б. КОЛОБОВ
Контрольные задачи практикума предназначены для студентов всех специальностей факультета заочного обучения ИГЭУ и могут быть использованы в качестве учебного материала студентами, обучающимися по дневной форме.
Утверждены цикловой методической комиссией электромеханического факультета
кафедра теоретической и прикладной механики ГОУВПО «Ивановский государственный энергетический университет имени В.И. Ленина»
 |
СОДЕРЖАНИЕ
| Указания к выполнению контрольной работы. |
| Задача №1. Равновесие плоской системы параллельных сил. |
| Задача №2. Равновесие плоской системы сил (Общий случай)…. |
| Задача №3. Кинематика точки…………..…………. |
| Задача №4. Плоское движение твердого тела……. |
| Задача №5. Сложное движение точки……………. |
| Задача №6. Динамика точки……………………….. |
| Задача №7. Колебания материальной точки………. |
| Задача № 8. Принцип Даламбера…………………. |
УКАЗАНИЯ К ВЫПОЛНЕНИЮ
КОНТРОЛЬНОЙ РАБОТЫ
Контрольная работа студента-заочника состоит из двух частей:
— контрольная работа №1, включающая в себя задачи 1–5 (статика и кинематика);
— контрольная работа №2, состоящая из задач 6–10 (динамика).
Число задач может быть уменьшено решением кафедры, при согласовании с деканатом факультета заочного обучения. В этом случае студенты информируются дополнительным указанием.
Прежде, чем приступить к решению задач, студент должен внимательно изучить следующие темы по учебнику (например, Тарг С.М. Краткий курс теоретической механики. –М,: Высш.шк., 1995).
- Основные типы связей и их реакции.
- Момент силы, пара сил и их свойства.
- Условия и уравнения равновесия для различных систем сил.
- Кинематика точки.
- Простейшие виды движения твердого тела (поступательное и вращение вокруг твердой оси).
- Плоскопараллельное движение твердого тела.
- Сложное движение точки.
- Динамика точки.
- Прямолинейные колебания точки.
- Общие теоремы движения.
- Принцип Даламбера.
Свой вариант студент определяет по двум последним цифрам зачетной книжки (т.е. если, например, номер зачетной книжки заканчивается цифрами 12, то Ваш вариант 12, если 05 – вариант 5 и т.д.).
Если номер зачетной книжки заканчивается числом большим, чем число вариантов задания, то номер Вашего варианта определяется разностью двух последних цифр зачетной книжки и числом вариантов. Например: две последние цифры зачетной книжки – 31. Задание имеет 28 вариантов. Ваш вариант – 3 (31–28=3). Варианты задач указаны на рисунках в кружках.
Многие величины, определяемые в ходе решения, являются векторными, поэтому следует не только найти их модуль, но и указать на рисунке направления этих векторов (а также их компонентов).
Для удобства на каждый тип задач рассмотрен пример. С целью экономии места рисунки заданий примеров часто расположены в тексте решения задачи.
Решения задач следует сопровождать краткими комментариями, рисунки выполняться с помощью чертежных инструментов. Расчеты ведутся с точностью до третьей значащей цифры. Почерк должен быть разборчивым. Если записи допускают двойную трактовку, то они считаются ошибочными.
В тетради должны быть предусмотрены поля для замечаний проверяющего.
Задачи, выполненные с отклонением от вышеизложенных указаний, не проверяются и считаются незачтёнными.
ЗАДАЧА №1
РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ СИЛ
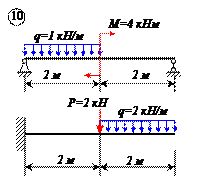
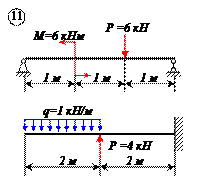
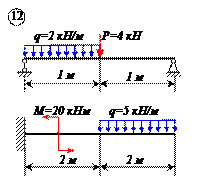
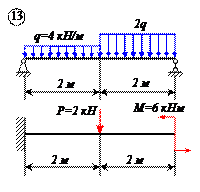
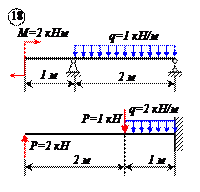
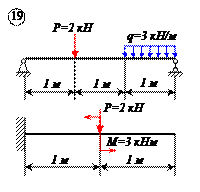
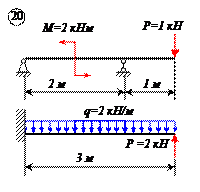
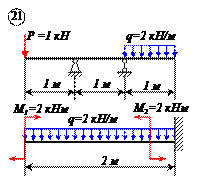
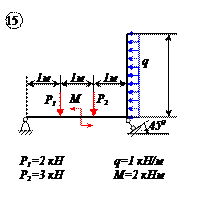
Определить реакции связей для балок, изображенных на рисунке.
Примечание: каждый вариант включает в себя две схемы балок.
Балка АВ весом Р и длиной l заделана правым концом в стену. В точке А на балку действует вертикальная сила F. Определить реакцию стены.
Отбросим связь–стену и заменим её действие реакцией (рис.в). Горизонтальная составляющая реакции стены равна в данном случае нулю, так как все активные силы, действующие на балку, вертикальны. Реакция стены состоит из вертикальной составляющей RB и пары сил с моментом М.
Выбираем оси координат: ось х направлена по балке АВ, ось у – по вертикали из точки А.
Запишем уравнение равновесия. Для плоской системы параллельных сил имеем два уравнения равновесия. Возьмём следующие уравнения – сумму проекций сил на ось у и сумму моментов всех сил относительно точки В:
Из первого уравнения находим силу 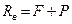
Из второго уравнения определяем момент пары сил 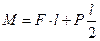
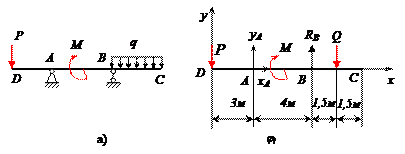
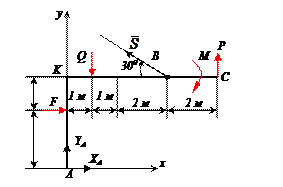
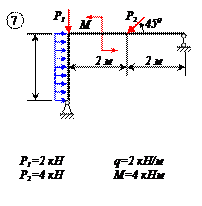
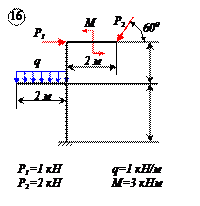
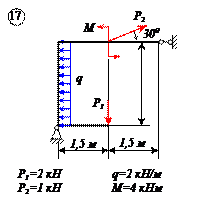
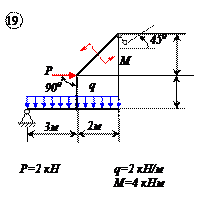
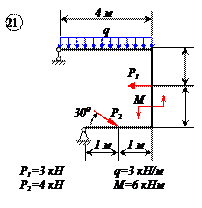
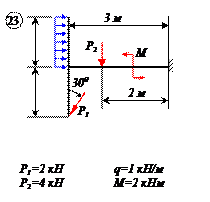
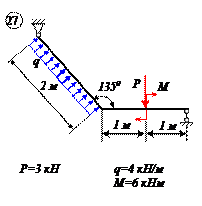
Двухконсольная горизонтальная балка шарнирно закреплена в точке А и опирается на каток в точке В. На балку действует вертикальная сила Р=20 Н, приложенная в точке D, равномерно распределённая вертикальная нагрузка на участке ВС интенсивностью q=25 Н/м и пара сил, момент которой равен М=40 Нм. Длины участков: AD=3 м, АВ=4 м, ВС=3 м. Определить реакции опор, пренебрегая весом балки.
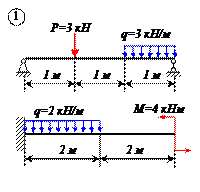
Отбросим мысленно связи и заменим их реакциями. Реакция в точке В RВ направлена по вертикали. Реакция шарнира А может иметь любое направление в плоскости. Поэтому заменяем её двумя составляющими ХА и УА . Распределённую нагрузку заменим силой 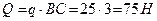
Проведем оси координат (рис.в) и запишем уравнения равновесия. Так как проекция силы ХА является единственной силой, проецирующейся на ось Х, то, следовательно, ХА=0.
Заметим, что сумма проекций сил, образующих пару, на любую ось равна нулю, так как силы, образующие пару сил, равны Модулу, параллельны и направлены в противоположные стороны.
Итак, учитывая, что ХА=0, имеем систему параллельных сил. Записываем для такой системы два уравнения равновесия, при этом следует стремиться к таким уравнениям равновесия, в каждое из которых входила бы только одна неизвестная величина. Для двухопорных балок это сумма моментов относительно опор.
Для проверки решения можно составить «лишнее» уравнение равновесия.
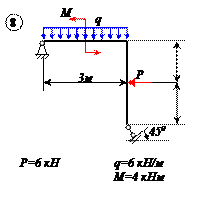
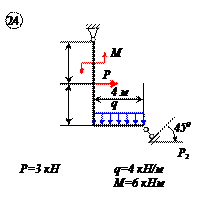
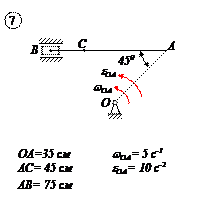
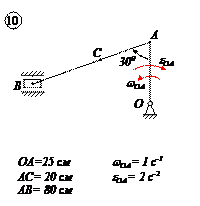
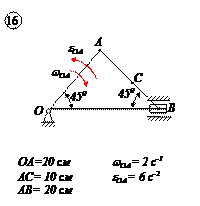
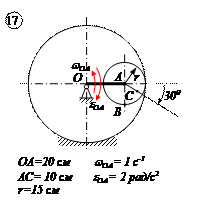
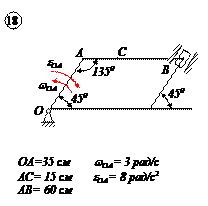
Варианты задачи 1.
 | 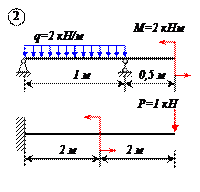 |
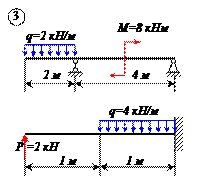 | 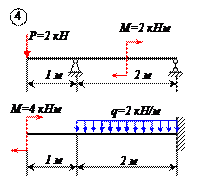 |
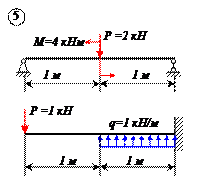 | 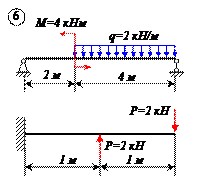 |
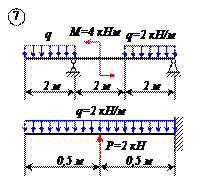 | 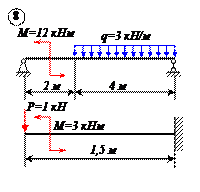 |
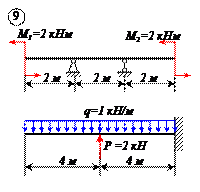 |  |
 |  |
 | 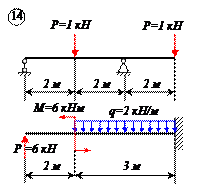 |
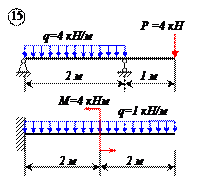 | 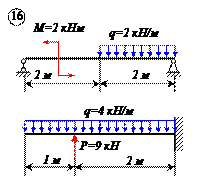 |
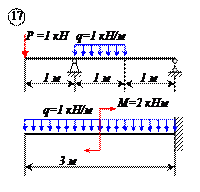 |  |
 |  |
 | 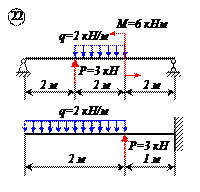 |
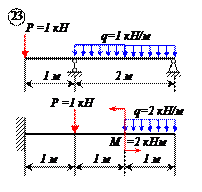 | 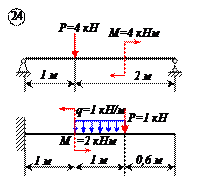 |
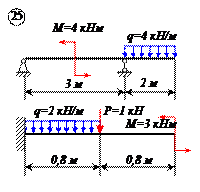 | 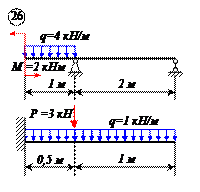 |
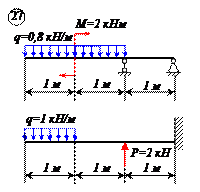 | 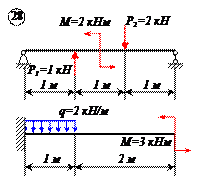 |
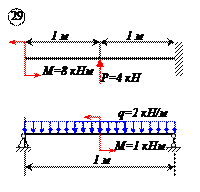 |  |
ЗАДАЧА №2
РАВНОВЕСИЕ ПЛОСКОЙ
СИСТЕМЫ СИЛ
(общий случай)
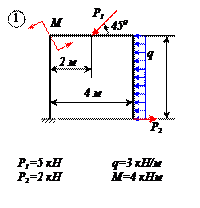
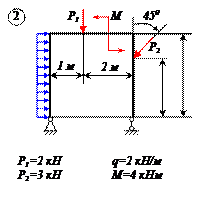
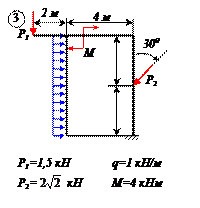
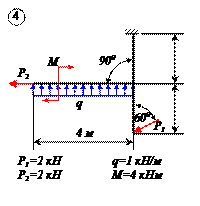
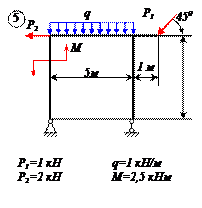
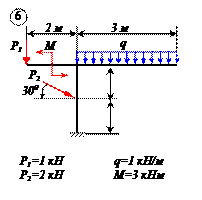
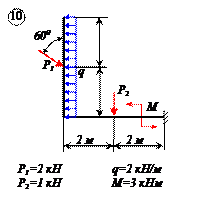
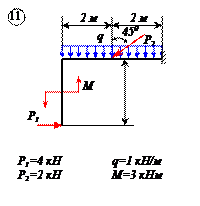
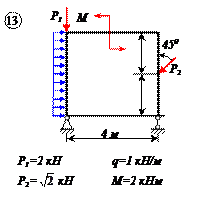
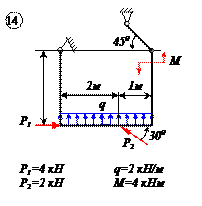
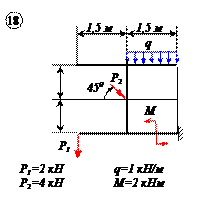
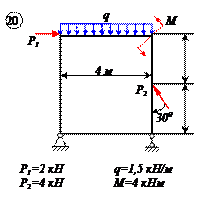
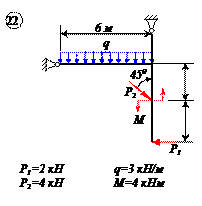
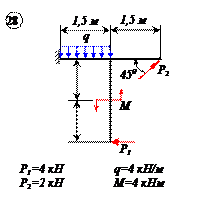
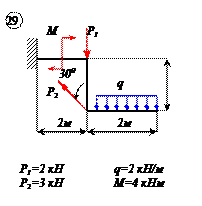
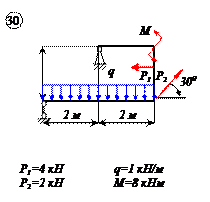
Найти реакции связей рамы, схема которой представлена на рисунке.
  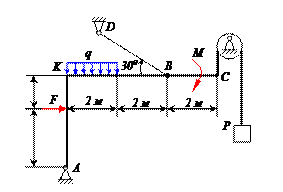 | Дано: F = 10 кН, P = 5 кН, M = 8 кНм, q = 0,5 кН/м. Определить реакцию опоры А и реакцию стержня BD. |
На раму наложены следующие связи: шарнирно-неподвижная опора, стержень BD и нить. Отбросим связи, заменив их силами.
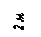
Так как направление реакции шарнирно-неподвижной опоры А неизвестно, то определим её составляющие 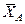
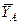

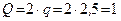
Для плоской системы сил, приложенных к раме, составим три уравнения равновесия:
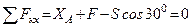
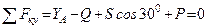
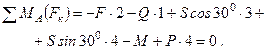
Момент от силы S найден с использованием теоремы Вариньона: момент равнодействующей равен сумме моментов составляющих.
Из уравнения (3) находим
Ответ: 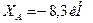
Знаки минус в значениях ХА и УА указывают на то, что принятые направления этих сил противоположны действительным.
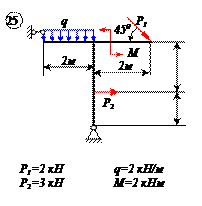
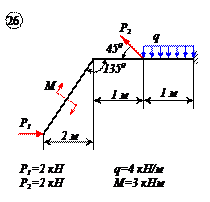
Варианты задачи 2.
  |     |
    |    |
  | 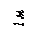 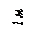  |
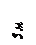   |    |
 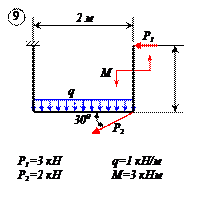 |    |
  | 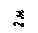 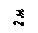  |
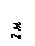  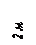  | 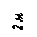  |
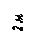  | 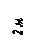 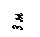  |
  |    |
   |    |
   |    |
    |    |
   |  |
 |    |
  |   |
ЗАДАЧА №3
КИНЕМАТИКА ТОЧКИ
По заданным уравнениям движения точки М найти и изобразить на рисунке вид её траектории. Для момента времени 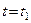
Варианты задачи 3.
| № варианта | Уравнения движения | 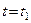 (с) (с) |
| Х=Х(t) м | Y=Y(t) м | |
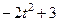 | 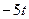 | 0,5 |
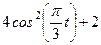 | 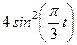 | |
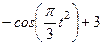 | 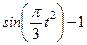 | |
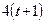 | 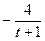 | |
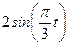 | 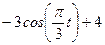 | |
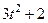 | 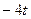 | 0,5 |
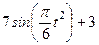 | 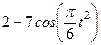 | |
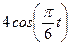 | 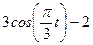 | |
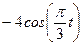 | 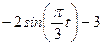 | |
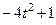 | 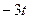 | 0,5 |
| № варианта | Уравнения движения | 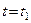 (с) (с) |
| Х=Х(t) м | Y=Y(t) м | |
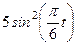 | 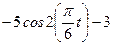 | |
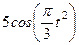 | 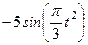 | |
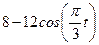 | 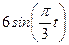 | |
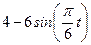 | 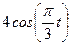 | |
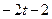 | 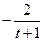 | |
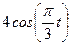 | 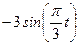 | |
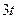 | 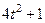 | 0,5 |
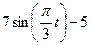 | 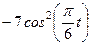 | |
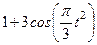 | 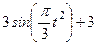 | |
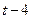 | 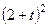 | |
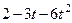 | 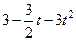 | |
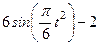 | 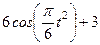 | |
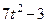 | 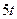 | 0,25 |
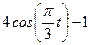 | 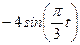 |
| № варианта | Уравнения движения | 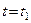 (с) (с) |
| Х=Х(t) м | Y=Y(t) м | |
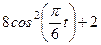 | 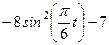 | |
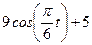 | 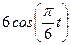 | |
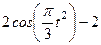 | 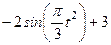 | |
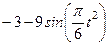 | 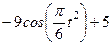 | |
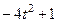 | 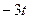 | |
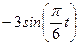 | 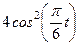 |
УКАЗАНИЯ. В некоторых вариантах при определении траектории следует учесть известные из тригонометрии формулы:
Касательное ускорение можно находить по формуле
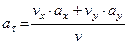
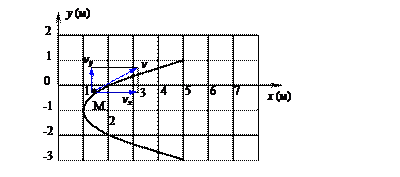
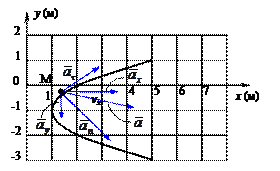
Даны уравнения движения точки в плоскости ху :
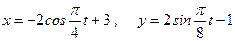
где х, у – в метрах, t – в секундах.
Определить уравнение траектории точки для момента времени t1=1 с найти скорость и ускорение точки, а также её касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
1. Для определения уравнения траектории точки исключаем из уравнений движения t. Поскольку t входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу
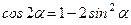
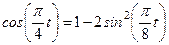
Из уравнений движения находим выражения соответствующих функций и подставляем их в предыдущее выражение:
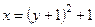
Строим график этой функции, представляющий собой в данном случае параболу.
Определим положение точки на траектории:

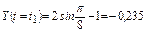
2. Скорость точки найдём по её проекциям на координатные оси:
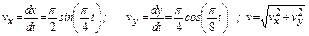
3. Аналогично найдём ускорение точки:
4. Касательное ускорение найдём по формуле
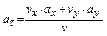
Подставляя ранее найденные числовые значения, получаем
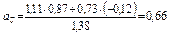
5. Нормальное ускорение
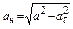
Изобразим вектор ускорения точки и его составляющие, причём правильность решения контролируем как по составляющим 

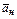
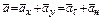
6. Радиус кривизны траектории 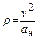
Подставляя численные значения, находим
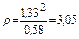
Ответ: v = 1,33 м/с, а = 0,88 м/с 2 , аt = 0,88 м/с 2 , ан= 0,58 м/с 2 ,
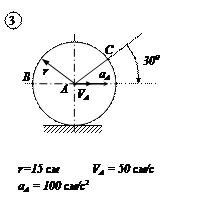
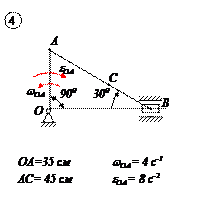
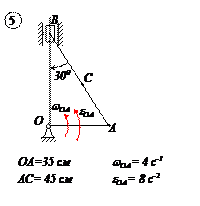
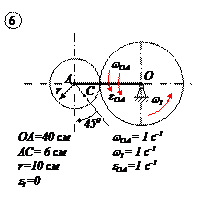
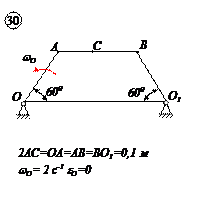
ЗАДАЧА №4
ПЛОСКОЕ ДВИЖЕНИЕ
ТВЕРДОГО ТЕЛА
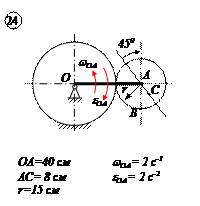
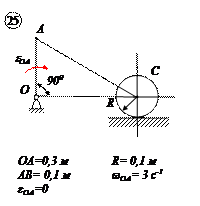
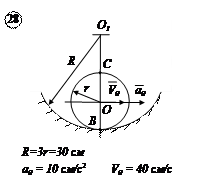
Для заданного положения механизма найти:
1. Скорости точек В и С и угловую скорость тела, которому они принадлежат.
2. Ускорение этих точек и угловое ускорение указанного в пункте 1 тела.
Примечание: внимательно ознакомьтесь с указаниями кафедры. Возможно, пункт 2 этой задачи выполнять не следует.
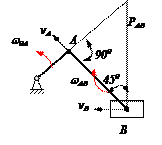
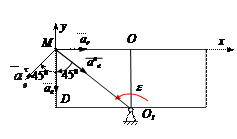
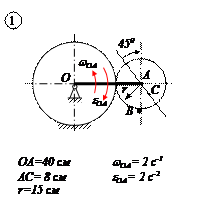
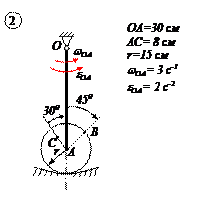
Для кривошипно-ползунного механизма найти скорость и ускорение точки В, а также угловую скорость и угловое ускорение шатуна АВ в момент, когда кривошип и шатун взаимно перпендикулярны и образуют с горизонтальной осью углы a = 45° и b = 45°.
1. Определение скоростей точек.
Вычисляем скорость пальца А кривошипа 0А. 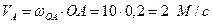
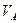
Скорость ползуна В направлена по горизонтали. Мгновенный центр скоростей РАВ шатуна АВ находится в точке пересечения перпендикуляров, проведённых их точек А и В к их скоростям.
Угловая скорость звена АВ 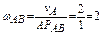
Скорость точки В 
Здесь АРАВ= 1 м и ВРАВ= 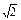
Скорость точки В можно найти также по теореме о проекциях скоростей двух точек:
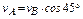
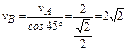
2. Определение ускорения точек.
Ускорение точки А складывается из нормального и касательного ускорений:
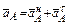
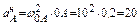
Касательное ускорение 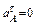
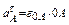
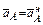
Согласно теореме об ускорениях точек плоской фигуры имеем
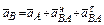
Нормальное ускорение В относительно A
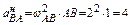
Касательное ускорение 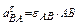
Строим многоугольник ускорений. При этом воспользуемся тем, что прямая, по которой направлено ускорение 
Ползун В движется по горизонтальной прямой, вдоль которой направлено и ускорение точки В. Отложим из точки В последовательно векторы 
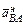
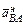
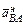
Проектируя векторное равенство на оси х и у, получаем
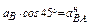
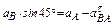
Из этих уравнений найдём аВ и 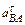
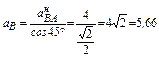
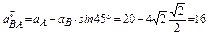
3. Нахождение углового ускорения звена АВ.
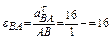
Ответ: 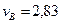
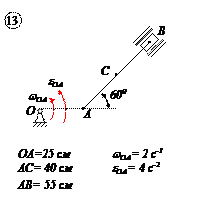
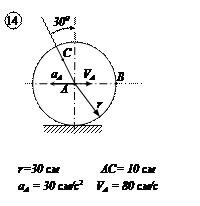
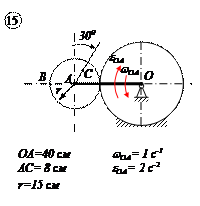
Варианты задачи 4.
 |  |
 |  |
 |  |
 |  |
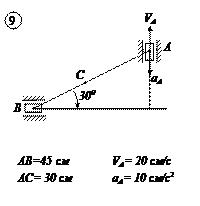 |  |
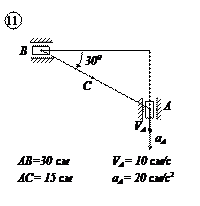 | 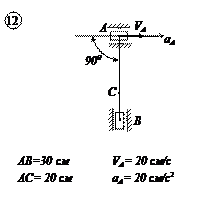 |
 |  |
 |  |
 |  |
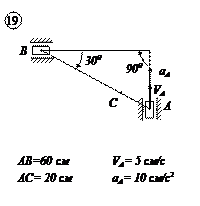 | 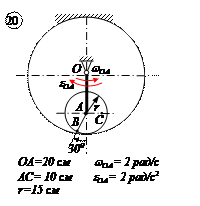 |
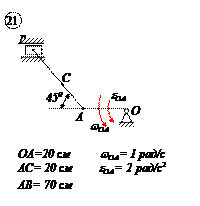 | 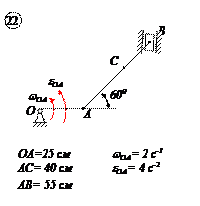 |
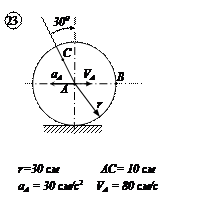 |  |
 |  |
 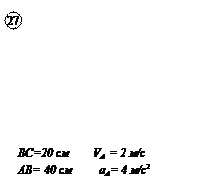 |  |
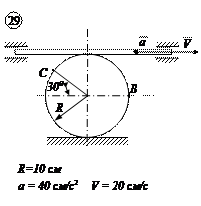 |  |
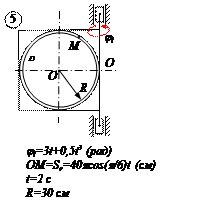
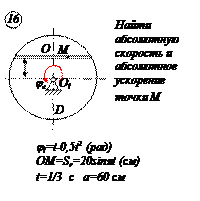
ЗАДАЧА №5
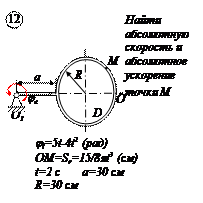
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
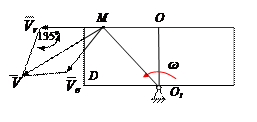
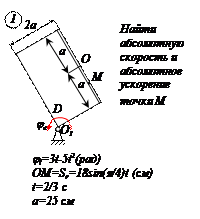
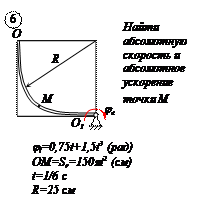
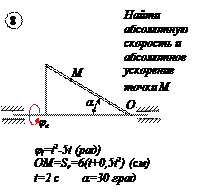
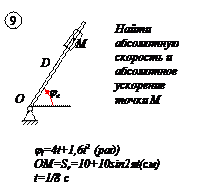
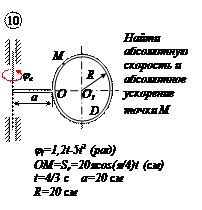
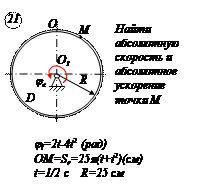
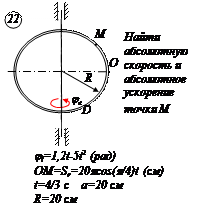
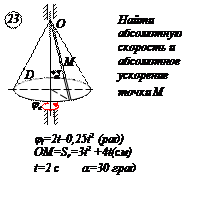
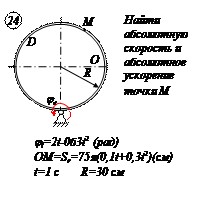
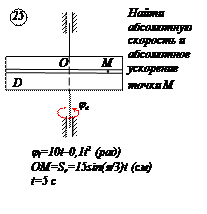
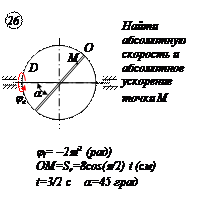
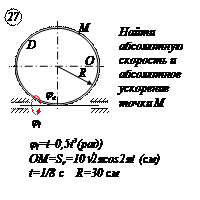
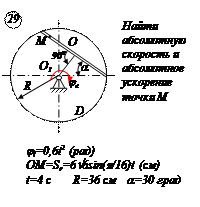
По заданным равнением относительного движения точки М неровного движения тела Д определить для момента времени 
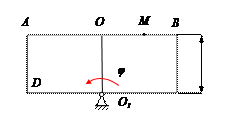
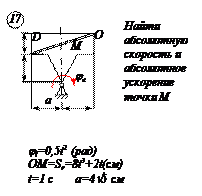
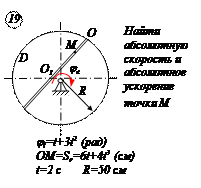
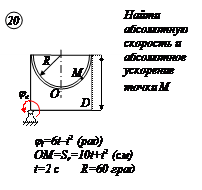
Прямоугольная пластина Д вращается вокруг неподвижной оси, проходящей через точку А , по закону 
В пластине вдоль прямой АВ движется точка М. закон её относительного движения задан уравнением
(В в метрах,t– в секундах)
Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t=1с.
РЕШЕНИЕ
Находим положение точки М в момент времени t1:
Отрезок ОМ =0,6 м откладываем в лево от точки 0,поскольку на отрезке показана точка М при положительных значениях ОМ от точки 0.
Абсолютную скорость точки М найдём как геометрическую сумму относительной и переносной скоростей:
Модуль относительной скорости
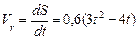
При t=1c
Направление 
Модуль переносной скорости
где 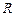
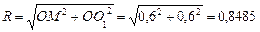
ω–угловая скорость тела,
При 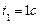
Теперь посчитаем 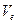
Направление 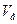
Абсолютную скорость 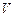
Остановимся на втором варианте.
При
Абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориорисова ускорений:
Модуль относительного ускорения
При
Переносное ускорение равно геометрической сумме нормальной касательной составляющих:
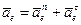
Модуль нормальной составляющей
При
Касательное ускорение 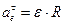
Где 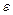
При
Колирисово ускорение находится по формуле
Модуль этого ускорения
Так как 
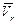
При
Направление 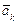
Покажем направления составляющих абсолютного ускорения на рисунке.
Модуль абсолютного ускорения точки М находим через проекции:
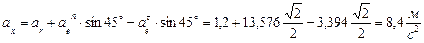
Ответ: при 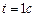
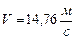
Варианты задачи 5.
 | G  | ||
  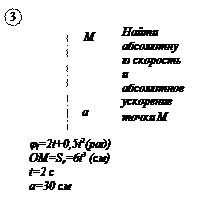 |  | ||
|  | ||
 |  | ||
 |  | ||
  |  |
 |  | ||
 |
| ||
   |  | ||
 |   | ||
 |  | ||
 |  | ||
 |  | ||
 |
| ||
 | 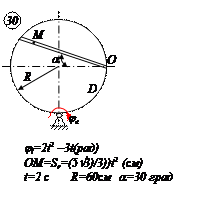 |
ЗАДАЧА №6
ДИНАМИКА ТОЧКИ
Груз D массой m ,получив в точке А начальную скорость 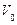
На участке АВ на груз, кроме силы тяжести действуют сила сопротивления среды 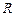
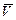
В точки В груз не изменяя величины своей скорости переходит на участок ВС трубы, где на него, помимо силы тяжести действует сила трения (коэффициент трения груза о трубу f=0.2) и переменная силаF, проекция которой Fx на ось Х задаётся.
Считая груз материальной точкой и зная расстояние АВ=l или время t1 движения груза от точки А до точки В ,найти закон движения груза на участке ВС, т.е. ВД=Х(t)
Примечание: каждый рисунок относится к двум вариантам задачи.
Пример. На участке АВ на груз D действует постоянная сила 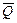
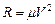
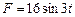
Определить закон движения груза на участке ВС при следующих условиях :m=8 кг, Q=20 Н, 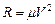
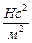
РЕШЕНИЕ
1.рассотрим движение груза на участке АВ. Составим дифференциальное уравнение движения на этом участке:
или
где для сокращения записей введено обозначения 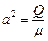
Разделив переменную и интегрируя обе части равенства, получим
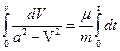
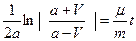
Из последнего выражения найдем V:
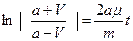
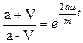
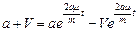
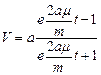
Учитывая, что 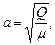
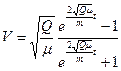
Пологая 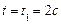
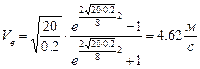
- теперь рассмотрим движение груза на участке ВС. Найденная скорость Vв будет для движения на этом участке начальной скоростью.
Составим дифференциальные уравнение движение груза:

где 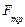
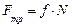
для горизонтального участка сила нормального давления груза на трубу 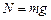
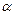
Разделим правую и левую части дифференциального уравнения на 
Умножим правую и левую части на 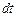
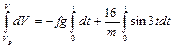
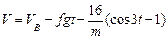
или 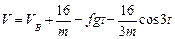
Выразим скорость груза через производную от координаты Х:
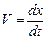
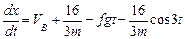
Умножим правую и левую части на 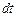
http://isopromat.ru/teormeh/obzornyj-kurs/uravnenia-ravnovesia-sistemy-sil
http://lektsii.org/11-31888.html