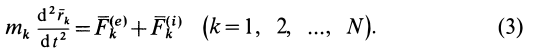Дифференциальное уравнение движения системы в теоретической механике

Дифференциальное уравнение движения системы:

Пусть даны внешние и внутренние силы, действующие на систему, состоящую из

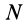
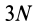
Систему дифференциальных уравнений (3) называют дифференциальными уравнениями движения механической системы в векторной форме. Если спроецировать векторные дифференциальные уравнения (3) на прямоугольные декартовы оси координат, то получим систему дифференциальных уравнений, описывающих движение точек механической системы. Для нахождения движения механической системы по заданным силам и начальным условиям для каждой точки системы нужно проинтегрировать, следовательно, систему дифференциальных уравнений. Эту задачу не удается точно решить в общем случае даже для одной точки. Она исключительно трудна в случае двух материальных точек, которые движутся только под действием сил взаимодействия по закону всемирного притяжения (задача о двух телах) и совершенно неразрешима в случае трех взаимодействующих точек (задача о трех телах).

Задача интегрирования дифференциальных уравнений механической системы еще сложнее, если на механическую систему наложены связи, силы реакций которых заранее не известны и должны быть дополнительно определены по заданным силам и связям аналогично случаю движения несвободной материальной точки по поверхности и кривой линии.

В некоторых случаях из дифференциальных уравнений движения системы можно получить первые интегралы, т. е. соотношения, в которые не входят производные второго порядка от координат по времени.

Если известны первые интегралы, то задача интегрирования системы дифференциальных уравнений облегчается. Хотя отдельные первые интегралы и не могут полностью описать движения всех точек системы, однако они иногда характеризуют важные стороны движения системы в целом.

Первые интегралы системы дифференциальных уравнений удобно получать из так называемых общих теорем динамики, когда выполняются некоторые дополнительные условия для действующих сил. Кроме того, общие теоремы динамики, даже когда по ним нельзя определить первые интегралы, дают ценную информацию о движении точки или системы. В некоторых задачах, где не требуется полного знания движения системы, эти сведения могут оказаться достаточными.

Общие теоремы динамики являются следствиями системы дифференциальных уравнений движения точки или соответственно системы точек.

• Теоремы об изменении количества движения и о движении центра масс
• Теорема об изменении кинетического момента
• Теорема об изменении кинетической энергии
• Потенциальное силовое поле
• Движение несвободной материальной точки
• Относительное движение материальной точки
• Геометрия масс
• Свойства внутренних сил системы

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Теоретическая механика: Решебник Яблонского:
Динамика механической системы (Д7, Д8, Д9, Д10, Д11, Д12, Д13)

Бесплатный онлайн решебник Яблонского. Выберите задание и номер варианта для просмотра решения. Смотрите также способы и примеры решения задач в разделе основные теоремы динамики.

Задание Д.7. Применение теоремы о движении центра масс к исследованию движения механической системы

Тела 1 и 2 (рис. 140–142) движутся по отношению к телу 3 с помощью механизмов, установленных на этом теле (силы, приводящие в движение механизмы, являются внутренними силами данной механической системы). Тело 3 находится на горизонтальной плоскости.

1. Предполагая горизонтальную плоскость гладкой, определить зависимость между перемещением s₃=s₃(t) тела 3 и относительным перемещением s_1r=s_1r(t) тела 1 (по отношению к телу 3), если механическая система в начале рассматриваемого движения (t=0) находилась в состоянии покоя, причем s_1r0=s_2r0=s₃₀=0; определить величину горизонтальной составляющей реакции R_x одного из упоров, которые удерживали бы тело 3 от перемещения.

2. Предполагая горизонтальную плоскость шероховатой, написать дифференциальное уравнение движения тела 3; определить условие, при котором тело 3 (при заданных параметрах системы) придет в движение, и найти зависимость между s₃(t) и s_1r(t), считая, что дальнейшее движение происходит при соблюдении этого условия (при t=0 s’_1r0=s’2_2r0=s’₃₀=0, s_1r0=s_2r0=s₃₀=0).

Известны: m₁, m₂ – массы тел 1 и 2; m₃ – масса тела 3 с находящимися на нем механизмами привода (центр масс C₃ по отношению к телу 3 не перемещается); R, r – радиусы больших и малых окружностей тел 1 и 2 или звеньев A и B механизмов привода; α, β – углы наклона граней призм (тел 3) и лент транспортеров к горизонтальной плоскости; f_сц, f – коэффициенты трения покоя (сцепления) и трения скольжения соответственно, принимаемые одинаковыми во всех вариантах: f_сц=0,11, f=0,10; s_1r=s_1r(t) – непрерывная и возрастающая функция времени (ее производная тоже непрерывна и возрастает).

Качение тел происходит без проскальзывания; нити невесомы и нерастяжимы.

На схемах тела 1, 2, 3 – в отклоненных от начального (t=0) положениях; показаны относительные перемещения s_1r, s_2r тел 1 и 2 и предполагаемое абсолютное перемещение s₃ тела 3 в сторону возрастания этих перемещений. Необходимые для решения данные приведены в табл. 43. Массой зубчатой рейки (варианты 1, 6, 7, 14, 15, 20, 22, 29) пренебречь.

Варианты с решением: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 30 (решено 97%)

Задание Д.8. Применение теоремы об изменении количества движения к исследованию движения механической системы

Механическая система (рис. 144–146) состоит из тел 1, 2, 3 с массами соответственно m₁, m₂ и m₃. Массами остальных тел, составляющих систему, пренебречь.

На тело 1 наложены две связи. Опора A препятствует перемещению по нормали к опорным поверхностям (по вертикали). Опора B не препятствует перемещениям по вертикали и горизонтали, но исключает возможность поворота.

В некоторый момент времени (принятый за начальный), когда скорость тела 1 равна v₀, а угловая скорость тела 2 – ω₂₀, движение тел 2 и 3 относительно тела 1 начинает замедляться (направление вращения тела 2 и направление скорости v₀ показаны на рис. 144–146). Торможение осуществляется внутренними для всей системы силами. Устройство, осуществляющее торможение, на схемах не показано. В процессе торможения угловое ускорение ε₂ (замедление) тела 2 остается постоянным.

Определить скорость v_т тела 1 в тот момент времени, когда ω₂ становится равным нулю, т. е. относительное движение тел 2 и 3 прекращается. Вычисление v_т произвести для одного из следующих условий:

а) на тело 1 со стороны направляющих A действует сила кулоновского (сухого) трения F=-f|N|v/|v| (f – коэффициент трения скольжения, |N| — модуль реакции в точке A);

б) на тело 1 кроме силы трения скольжения F в опоре A действует сила «вязкого» трения R со стороны опоры B: R=-bv (b – коэффициент «вязкого» сопротивления, v – вектор скорости тела 1).

Вычисление v_т произвести точно и приближенно. В приближенном расчете пренебречь величинами первого и более высоких порядков малости относительно промежутка времени Т=ω₂₀/ε₂.

Для всех вариантов принять v₀=2 м/с; ω₂₀=10 рад/с, ε₂=250 рад/с 2 ; f=0,25; b=10 Н*с/м.

Считать, что проскальзывание колес по соответствующим поверхностям отсутствует.

Необходимые для расчета данные приведены в табл. 44.

Варианты с решением: 1 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 21 25 26 28 30 (решено 70%)

Задание Д.9. Применение теоремы об изменении кинетического момента к определению угловой скорости твердого тела

Тело H массой m₁ вращается вокруг вертикальной оси z с постоянной угловой скоростью ω₀; при этом в точке O желоба AB тела H на расстоянии AO от точки A, отсчитываемом вдоль желоба, находится материальная точка K массой m₂. В некоторый момент времени (t=0) на систему начинает действовать пара сил с моментом M_z=M_z(t). При t=τ действие сил прекращается.

Определить угловую скорость ω_τ тела H в момент t=τ.

Тело H вращается по инерции с угловой скоростью ω_τ.

В некоторый момент времени t₁=0 (t₁ – новое начало отсчета времени) точка K (самоходный механизм) начинает относительное движение из точки O вдоль желоба AB (в направлении к B) по закону OK=s=s(t₁).

Определить угловую скорость ω_T тела H при t₁=T.

Тело H рассматривать как однородную пластинку, имеющую форму, показанную на рис. 148–150. Необходимые для решения данные приведены в табл. 45–46.

Примечание. Знак минус перед M_z и ω соответствует направлению вращения часовой стрелки, если смотреть со стороны положительного направления оси z.

Варианты с решением: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 (решено 100%)

Задание Д.10. Применение теоремы об изменении кинетической энергии к изучению движения механической системы

Механическая система под действием сил тяжести приходит в движение из состояния покоя; начальное положение системы показано на рис. 152–154. Учитывая трение скольжения тела 1 (варианты 1–3, 5, 6, 8–12, 17–23, 28–30) и сопротивление качению тела 3, катящегося без скольжения (варианты 2, 4, 6–9, 11, 13–15, 20, 21, 24, 27, 29), пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорость тела 1 в тот момент, когда пройденный им путь станет равным s.

В задании приняты следующие обозначения: m₁, m₂, m₃, m₄ – массы тел 1, 2, 3, 4; R₂, r₂, R₃, r₃ – радиусы больших и малых окружностей; i_2x, i_3ξ – радиусы инерции тел 2 и 3 относительно горизонтальных осей, проходящих через их центры тяжести; α, β – углы наклона плоскостей к горизонту; f – коэффициент трения скольжения; δ – коэффициент трения качения.

Необходимые для решения данные приведены в табл. 47. Блоки и катки, для которых радиусы инерции в таблице не указаны, считать сплошными однородными цилиндрами.

Наклонные участки нитей параллельны соответствующим наклонным плоскостям.

Варианты с решением: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 (решено 100%)

Задание Д.11. Исследование поступательного и вращательного движений твердого тела

Механическая система состоит из механизма (колес 1 и 2) и груза 3.

К колесу 1 приложена пара сил с моментом M=M(t) (движущий момент) или движущая сила P=P(t).

Время t отсчитывается от некоторого момента (t=0), когда угловая скорость колеса 1 равна ω₁₀. Момент сил сопротивления ведомого колеса 2 равен M_c. Другие силы сопротивления движению системы не учитывать.

Массы колес 1 и 2 равны m₁ и m₂, а масса груза 3 – m₃.

Радиусы больших и малых окружностей колес R₁, r₁, R₂, r₂.

Схемы механических систем показаны на рис. 156–158, а необходимые для решения данные приведены в табл. 48.

Найти уравнение движения тела системы, указанного в последней графе табл. 48.

Определить также натяжение нитей в заданный момент времени, а в вариантах, где имеется соприкасание колес 1 и 2, найти, кроме того, окружное усилие в точке их касания. Колеса 1 и 2, для которых радиусы инерции i_x1 и i_x2 в табл. 48 не заданы, считать сплошными однородными дисками.

Варианты с решением: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 (решено 100%)

Задание Д.12. Исследование плоского движения твердого тела

Определить значение постоянной силы P под действием которой качение без скольжения колеса массой m носит граничный характер, т. е. сцепление колеса с основанием находится на грани срыва.

Найти также для этого случая уравнение движения центра масс колеса C, если в начальный момент времени его координата x_C0=0 и скорость v_C0=0.

Варианты задания показаны на рис. 160–162, а необходимые для решения данные приведены в табл. 49.

В задании приняты следующие обозначения: i_C – радиус инерции колеса относительно центральной оси, перпендикулярной его плоскости; R и r – радиусы большой и малой окружностей; f_сц – коэффициент сцепления (коэффициент трения покоя); δ – коэффициент трения качения.

Примечание. Колеса, для которых радиусы инерции не указаны, считать сплошными однородными дисками.

Варианты с решением: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 (решено 100%)

Дифференциальные уравнения движения системы

Дифференциальные уравнения движения системы

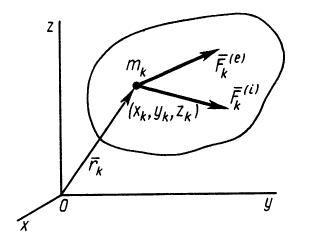
• Приложите внешнюю силу и внутреннюю силу, действующую на систему, состоящую из N точек (рис. 39). Если внешняя сила M » ‘и вся внутренняя сила F’1 приложены к каждой точке в системе, вы можете построить дифференциальное уравнение движения, например, для любой точки Арт в системе. w »0 = Ae, + FL ° (* = 1, 2, …, N). (3) Система дифференциальных уравнений (3) называется дифференциальным уравнением движения механической системы в векторном виде.

Кинетическая энергия машины, начиная с определенного момента, увеличивается или уменьшается в зависимости от того, превышает ли основная работа движущей силы основную работу сопротивления. Людмила Фирмаль

Проецирование векторного дифференциального уравнения (3) на декартовы декартовы оси дает систему дифференциальных уравнений 3 Вт, которые описывают движение точек в механической системе. Поэтому, чтобы найти движение механической системы в соответствии с условиями силы, заданными для каждой точки в системе, необходимо интегрировать систему дифференциальных уравнений 3N. Эта проблема не может быть решена точно, даже если это общая точка в общем случае.

• В случае двух материальных точек, которые движутся только под действием силы взаимодействия по универсальному закону притяжения (задача двух тел), это очень сложно, и случай трех точек взаимодействия (задача трех тел) не может быть полностью решен. Задача интегрирования дифференциального уравнения в механическую систему является более сложной, если механическая система ограничена и ее сила реакции заранее не известна, для перемещения несвободных материальных точек вдоль поверхностей и кривых. Как и в случае, он должен быть дополнительно определен с учетом приведенных сил и ограничений.

В некоторых случаях интегралы первого порядка могут быть получены из дифференциальных уравнений движения системы, то есть отношений, которые не включают производные второго порядка по временным координатам. Если вы знаете первый интеграл, задача интеграции системы дифференциальных уравнений становится проще. Отдельные начальные интегралы не могут полностью учитывать движение всех точек в системе, но могут характеризовать важные аспекты общего движения системы.

Если начальное отклонение и скорость груза также находятся в плоскости l, то маятник должен всегда находиться в плоскости l и быть закреплен на центральной рамке отсчета. Людмила Фирмаль

Первый интеграл системы дифференциальных уравнений может быть удобно получен из так называемой общей теоремы. Намики — это когда выполняются некоторые дополнительные требования действующего подразделения. Кроме того, общая теорема динамики дает ценную информацию о движении точек или систем, даже если исходные интегралы не могут быть определены из них. Эта информация может быть достаточной для некоторых задач, которые не требуют полного знания поведения системы. Общая теорема динамики является результатом дифференциальной системы уравнений движения точки или системы точек.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института