Составить каноническое уравнение параболы точка

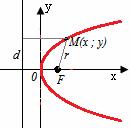
Парабола

Элементы параболы
0F — фокальная ось
0 — вершина
— фокус
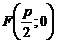
ε=1 — эксцентриситет
— фокальный радиус
— директриса
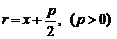
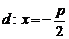
p — фокальный параметр

Каноническое уравнение параболы (ось Ox совпадает с фокальной осью, начало координат – с вершиной параболы): y 2 =2px
При p x 2 =2py
При p>0 ветви параболы направлены вверх, при p 2 /2+(y-1) 2 /2=1, необходимо набрать в поле x^2/2+(y-1)^2/2=1 и нажать кнопку График параболы .

Самостоятельно построить график можно, используя операцию выделения полного квадрата.

Каноническое уравнение параболы

Вы будете перенаправлены на Автор24

Парабола — это кривая, образованная геометрическим множеством точек, находящихся на одинаковом расстоянии от некой точки $F$, называемой фокусом и не лежащей ни на этой кривой, ни на прямой $d$.

То есть отношение расстояний от произвольной точки на параболе до фокуса и от этой же точки до директрисы всегда равно единице, это отношение называется эксцентриситетом.

Термин “эксцентриситет” также используется для гипербол и эллипсов.

Основные термины из канонического уравнения параболы

Точка $F$ называется фокусом параболы, а прямая $d$ — её директрисой.

Осью симметрии параболы называется прямая, проходящая через вершину параболы $O$ и её фокус $F$, так, что она образует прямой угол с директрисой $d$.

Вершиной параболы называется точка, расстояние от которой до директрисы минимальное. Эта точка делит расстояние от фокуса до директрисы пополам.

Что из себя представляет каноническое уравнение параболы

Каноническое уравнение параболы довольно простое, его несложно запомнить и оно имеет следующий вид:

$y^2 = 2px$, где число $p$ должно быть больше нуля.

Число $p$ из уравнения носит название «фокальный параметр».

Данное уравнение параболы, вернее именно эта наиболее часто применяемая в высшей математике формула, применимо в том случае, когда ось параболы совпадает с осью $OX$, то есть парабола располагается как будто на боку.

Парабола, описанная уравнением $x^2 = 2py$ — это парабола, ось которой совпадает с осью $OY$, к таким параболам мы привыкли в школе.

А парабола, которая имеет минус перед второй частью уравнения ($y^2 = — 2px$), развёрнута на 180° по отношению к каноничной параболе.

Готовые работы на аналогичную тему

Парабола является частным случаем кривой 2-ого порядка, соответственно, в общем виде уравнение для параболы выглядит точно также как для всех таких кривых и подходит для всех случаев, а не только когда парабола параллельна $OX$.

При этом дискриминант, вычисляющийся по формуле $B^2 – 4AC$ равен нулю, а само уравнение выглядит так: $Ax^2 + B \cdot x \cdot y + C\cdot y^2 + D\cdot x + E\cdot y + F = 0$

Вывод с помощью графика канонического уравнения для параболы

Рисунок 1. График и вывод канонического уравнения параболы

Из определения, приведённого выше в данной статье, составим уравнение для параболы с верхушкой, расположенной на пересечении координатных осей.

Используя имеющийся график, определим по нему $x$ и $y$ точки $F$ из определения параболической кривой, данного выше, $x = \frac

<2>$ и $y = 0$.

Для начала составим уравнение для прямой $d$ и запишем его: $x = — \frac

<2>$.

Для произвольной точки M, лежащей на нашей кривой, согласно определению, справедливо следующее соотношение:

$FM$ = $ММ_d$ (1), где $М_d$ — точка пересечения перпендикуляра, опущенного из точки $M$ c директрисой $d$.

Икс и игрек для этой точки равны $\frac

<2>$ $y$ соответственно.

Запишем уравнение (1) в координатной форме:

Теперь для того чтобы избавиться от корня необходимо возвести обе части уравнения в квадрат:

После упрощения получаем каноническое уравнение параболы: $y^2 = px$.

Парабола, описываемая с помощью квадратичной функции

Уравнение, описывающее параболу с верхушкой, расположенной где угодно на графике и необязательно совпадающей с пересечением осей координат, выглядит так:

Чтобы вычислить $x$ и $y$ для вершины такой параболы, необходимо воспользоваться следующими формулами:

$y_A = — \frac<4a>$, где $D = b^2 – 4ac$.

Пример составления классического уравнения параболы

Задача. Зная расположение фокусной точки, составить каноническое уравнение параболы. Координаты точки фокуса $F$ $(4; 0)$.

Так как мы рассматриваем параболу, график которой задан каноническим уравнением, то её вершина $O$ находится на пересечении осей икс и игрек, следовательно расстояние от фокуса до вершины равно $\frac<1><2>$ фокального параметра $\frac

<2>= 4$. Путём нехитрых вычислений получим, что сам фокальный параметр $p = 8$.

После подстановки значения $p$ в каноническую форму уравнения, наше уравнение примет вид $y^2 = 16x$.

Как составить уравнение параболы по имеющемуся графику

Рисунок 2. Каноническое уравнение для параболы график и пример для решения

Для начала необходимо выбрать точку $М$, принадлежащую графику нашей функции, и, опустив из неё перпендикуляры на оси $OX$ и $OY$, записать её икс и игрек, в нашем случае точка $M$ это $(2;2)$.

Теперь нужно подставить полученные для этой точки $x$ и $y$ в каноническое уравнение параболы $y^2 = px$, получаем:

Сократив, получаем следующее уравнение параболы $y^2 = 2 \cdot x$.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 03 12 2021

Парабола: формулы, примеры решения задач

Определение параболы. Параболой называется множество всех точек плоскости, таких, каждая из которых находится на одинаковом расстоянии от точки, называемой фокусом, и от прямой, называемой директрисой и не проходящей через фокус.

Каноническое уравнение параболы имеет вид:

,

где число p, называемое параметром параболы, есть расстояние от фокуса до директрисы.

На чертеже линия параболы — бордового цвета, директриса — ярко-красного цвета, расстояния от точки до фокуса и директрисы — оранжевого.

В математическом анализе принята другая запись уравнения параболы:

то есть ось параболы выбрана за ось координат. Можно заметить, что ax² — это квадратный трёхчлен ax² + bx + c , в котором b = 0 и c = 0 . График любого квадратного трёхчлена, то есть левой части квадратного уравнения, будет параболой.

Фокус параболы имеет координаты

Директриса параболы определяется уравнением .

Расстояние r от любой точки параболы до фокуса определяется формулой .

Для каждой из точек параболы расстояние до фокуса равно расстоянию до директрисы.

Пример 1. Определить координаты фокуса параболы

Решение. Число p расстояние от фокуса параболы до её директрисы. Начало координат в данном случае — в роли любой точки, расстояния от которой от фокуса до директрисы равны. Находим p:

Находим координаты фокуса параболы:

Пример 2. Составить уравнение директрисы параболы

Решение. Находим p:

Получаем уравнение директрисы параболы:

Пример 3. Составить уравнение параболы, если расстояние от фокуса до директрисы равно 2.

Решение. Параметр p — это и есть данное расстояние от фокуса до директрисы. Подставляем и получаем:

Траектория камня, брошенного под углом к горизонту, летящего футбольного мяча или артиллерийского снаряда будет параболой (при отсутствии сопротивления воздуха). Зона достижимости для пущенных камней вновь будет параболой. В данном случае речь идёт об огибающей кривой траекторий камней, выпущенных из данной точки под разными углами, но с одной и той же начальной скоростью.

Парабола обладает следующим оптическим свойством: все лучи, исходящие из источника света, находящегося в фокусе параболы, после отражения оказываются направленными параллельно её оси. Это свойство параболы используется при изготовлении прожекторов, автомобильных фар, карманных фонариков, зеркала которых имеют вид параболоидов вращения (фигур, получающихся при вращении параболы вокруг оси). Пучок параллельных лучей, двигающийся вдоль оси параболы, отражаясь, собирается в её фокусе.