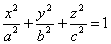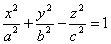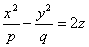Конические поверхности
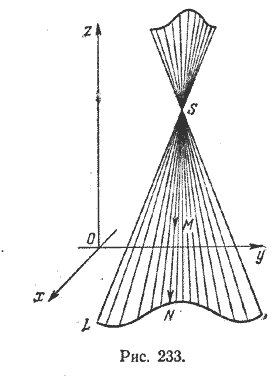
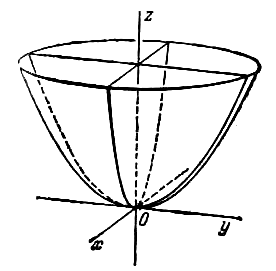
Объединение всех прямых, проходящих через каждую точку данной кривой и некоторую фиксированную точку пространства, не лежащую на этой кривой, называется конической поверхностью. Данная кривая называется направляющей, данная фиксированная точка — вершиной, а прямые — образующими конической поверхности (рис. 233).
Легко видеть, что конические поверхности состоят из двух полостей с общей вершиной.
Конические и цилиндрические поверхности обладают замечательным свойством: все они разворачиваются на плоскость без складок и разрывов, и, наоборот, из плоских листов материала, согнув их, можно получать поверхности конической и цилиндрической формы. Благодаря этому свойству они получили большое применение в технике.
Выведем уравнение конической поверхности. Если М — произвольная точка этой поверхности, отличная от вершины S, а N — точка пересечения образующей SM с направляющей L, то векторы \(\overrightarrow
\(\overrightarrow
Пусть для простоты кривая L лежит в плоскости хОу и имеет уравнение
а вершина S лежит на оси Oz и имеет координаты (0; 0; с), с =/= 0. Тогда’
\(\overrightarrow
где (х; у; z ) — координаты точки М, а (ξ ; η ) — координаты точки N на плоскости хОу. Из векторного равенства (1) получаем следующие равенства для координат:
Так как координаты ξ , η удовлетворяют уравнению (2), то координаты (х; у; z) удовлетворяют уравнению
Это и есть уравнение конической поверхности с вершиной в точке S (0; 0; с), с =/= 0, и направляющей F(х; у) = 0. Таким образом, уравнение конической поверхности (3) получается из уравнения направляющей (2) заменой х на \( \frac
Задача. Составить уравнение конической поверхности с вершиной в точке
(0; 0; с), с > 0, и направляющей
Данная коническая поверхность имеет уравнение
После соответствующих преобразований получаем искомое уравнение:
Составить уравнение конической поверхности вершина
Глава 46. Поверхности второго порядка
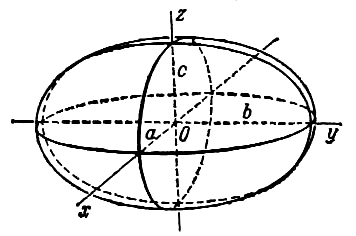
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
(1).
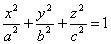
Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c — сжатым. В случае, когда a=b=c , эллипсоид представляет собой сферу.
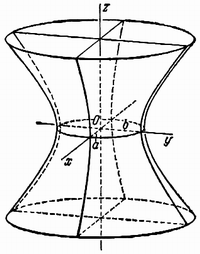
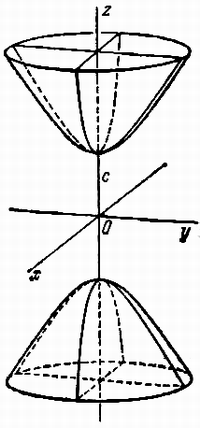
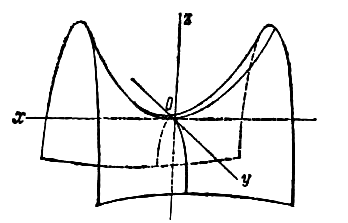
Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями
, (2)
. (3)
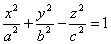
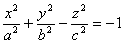
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), — двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b ) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.
Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями
, (4)
, (5)
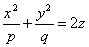
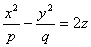
где p и q — положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), — гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q , параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).
Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).
Выберем какую-нибудь плоскость; обозначим ее буквой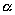 
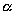
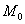
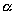
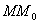
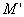
. Зададим, кроме того, некоторое положительное число q . Пусть М — произвольная точка пространства, не лежащая на плоскости 
, 
— основание перпендикуляра, опущенного на плоскость 
из точки М. Переместим точку М по прямой 
в новое положение 
так, чтобы имело место равенство
и чтобы после перемещения точка осталась с той же стороны от плоскости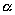 
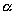
, где она была первоначально (рис. 6). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости 
; точки, которые расположены на плоскости 
, оставим на своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости 
, переместятся; при этом расстояние от каждой точки до плоскости 
изменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас перемещение точек пространства называется его равномерным сжатием к плоскости 
; число q носит название коэффициента сжатия.
Пусть дана некоторая поверхность F ; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F ’. Будем говорить, что поверхность F ’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).
ПРИМЕР. Доказать, что произвольный трехосный эллипсоид
может быть получен из сферы
в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия 
и к плоскости Oxz с коэффициентом сжатия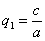 
.
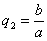
ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом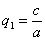 
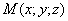
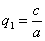
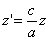
и пусть 
— точка, в которую переходит при этом точка 
. Выразим координаты x’, y’, z ’ точки М’ через координаты x, y, z точки М. Так как прямая MM ’ перпендикулярна к плоскости Oxy , то x’=x, y’=y . С другой стороны, так как расстояние от точки М’ до плоскости Oxy равно расстоянию от точки М до этой плоскости, умноженному на число 
, то 
.
Таким образом, мы получаем искомые выражения:
, 
, 
(6)
, 
, 
(7)
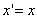
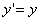
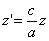
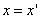
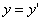
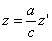
Предположим, что M(x; y; z ) — произвольная точка сферы
.
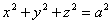
Заменим здесь x, y, z их выражениями (7); получим
,
.
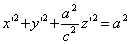
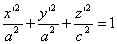
Следовательно, точка M’(x’; y’; z ’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам
, 
, 
;
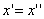
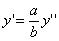
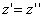
тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.
Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.
имеет две системы прямолинейных образующих, которые определяются уравнениями:
, 
;
, 
,
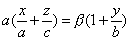
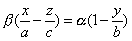
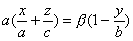
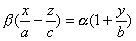
где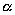 
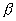
и 
— некоторые числа, не равные одновременно нулю. Гиперболический параболоид
также имеет две системы прямолинейных образующих, которые определяются уравнениями
, 
;
, 
.
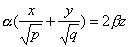
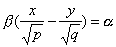
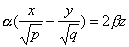
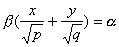
Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L . Точка S называется вершиной конуса; линия L — направляющей.
Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).
Тема: Линейные операции над векторами. Скалярное произведение векторов (стр. 7 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 |
В этом случае уравнение конической поверхности имеет вид
. (1)
Если направляющая является эллипсом с центром на оси Oz,
то получаем поверхность, называемую конусом второго порядка, уравнение этой поверхности имеет вид:
. (2)
Ось Oz в этом случае является осью конуса второго порядка.
Сечения конуса второго порядка:
Пусть плоскость p не проходит через вершину конуса второго порядка, тогда плоскость p пересекает конус:
а) по эллипсу, если p пересекает все образующие конуса;
б) по гиперболе, если p параллельна двум образующим конуса;
в) по параболе, если p параллельна одной образующей конуса.
2. Получите уравнение конической поверхности (1).
3. Получите уравнение конической поверхности второго порядка (2).
III. Основные типовые задачи.
Составление уравнения конической поверхности по координатам вершины и уравнению направляющей.
IV. Примеры решения задач.
Задача 1. Написать уравнение конической поверхности, вершина которой находится в начале координат, а направляющая задана уравнениями 
Пусть точка M(x, y, z) – произвольная точка конической поверхности. Проведем через эту точку образующую l, она пересечет направляющую в точке 
. Запишем канонические уравнения прямой l, как уравнения прямой, проходящей через точку N и вершину конуса О(0, 0, 0)
,
.
Выразим из последней системы 
и 
: 
, 
. Т. к. точка N лежит на направляющей конической поверхности, то ее координаты должны удовлетворять уравнениям направляющей:
(3)
Подставим найденные выражения во второе уравнение системы (3)
,
,
,
. (4)
, 
. (5)
Подставляем (4) и (5) в первое уравнение системы (3)
,
,
.
Полученное уравнение является искомым уравнением конической поверхности.
V. Задачи для самостоятельного решения.
1) Написать уравнение конической поверхности, если:
а) направляющая в плоскости xOy задана уравнением 
, а вершина имеет координаты (1; 0; 1);
б) направляющая в плоскости xOy задана уравнением 
, а вершина имеет координаты (0; 0; 1);
в) направляющая в плоскости xOy задана уравнением 
, а вершина имеет координаты (0; 0; 1).
г) направляющая в плоскости xOy задана уравнением 
, а вершина имеет координаты (0; 0; с).
2) Составить уравнение конической поверхности с вершиной в точке S(1; 2; 4), образующие которой составляют с плоскостью 
угол j=45°.
3) Написать уравнение конической поверхности, направляющая которой задана уравнениями 
а вершина находится в точке 
.
4) Найти уравнение конической поверхности с вершиной в начале координат, которая проходит через линию пересечения:
а) гиперболоида 
и сферы 
;
б) эллипсоида 
и плоскости 
.
5) Напишите уравнение круговой конической поверхности, если известны уравнения ее оси l: 
и координаты одной из ее точек М(3; –4; 5).
6) Доказать, что уравнение 
определяет конус с вершиной в начале координат.
I. Теоретические сведения.
Определение. Эллипсоидом называется множество точек пространства, координаты которых в некоторой системе координат удовлетворяют следующему уравнению
. (1)
Уравнение (1) называется каноническим уравнением эллипсоида. Числа a,b,c>0 – полуоси эллипсоида.
Из уравнения эллипсоида можно получить ряд свойств:
1) Все точки эллипсоида расположены внутри прямоугольного параллелепипеда, ограниченного плоскостями 
, 
, 
.
2) Плоскости симметрии эллипсоида: xOy, yOz, xOz;
оси симметрии эллипсоида: Ox, Oy, Oz;
центр симметрии эллипсоида: начало координат.
3) Вершинами поверхности называются точки пересечения с осями симметрии. Вершины эллипсоида: 
, 
, 
, 
.
Исследование эллипсоида методом сечений.
Рассмотрим сечения эллипсоида плоскостями, параллельными плоскостям симметрии.
1) Сечение плоскостью a, параллельной плоскости 
.
(2)
. (3)
а) Если 
, то линия пересечения эллипс, в частности, если 
, то 
, и в сечении мы получаем эллипс ;
б) если 
, то линия пересечения мнимый эллипс;
в) если 
, то линия пересечения пара мнимых пересекающихся прямых с действительной точкой пересечения.
2) Сечение плоскостью b, параллельной плоскости 
.
(4)
. (5)
а) Если 
, то линия пересечения эллипс, в частности, если , то 
, и в сечении мы получаем эллипс 
;
б) если 
, то линия пересечения мнимый эллипс;
в) если 
, то линия пересечения пара мнимых пересекающихся прямых с действительной точкой пересечения.
3) Сечение плоскостью g, параллельной плоскости 
.
(6)
. (7)
а) Если 
, то линия пересечения эллипс, в частности, если , то 
, и в сечении мы получаем эллипс 
;
б) если 
, то линия пересечения мнимый эллипс;
в) если 
, то линия пересечения пара мнимых пересекающихся прямых с действительной точкой пересечения.
На рис.1 показаны сечения эллипсоида координатными плоскостями.
4. Покажите, что координатные плоскости являются плоскостями симметрии эллипсоида.
5. Покажите, что координатные оси являются осями симметрии эллипсоида.
6. Покажите, что начало координат является центром симметрии эллипсоида.
7. Найдите уравнение линии, образующейся при пересечении эллипсоида 
с плоскостью xOy.
8. Пересекаются ли эллипсоид 
и плоскость 
?
III. Основные типовые задачи.
9. Составление канонического уравнения эллипсоида.
10. Исследование сечений эллипсоида.
IV. Примеры решения задач.
Задача 1. Написать каноническое уравнение эллипсоида, который проходит через точку 
и пересекает плоскость xOy по эллипсу 
.
Каноническое уравнение эллипсоида имеет вид . Плоскость xOy пересекает эллипсоид по эллипсу . По условию это уравнение имеет вид . Следовательно, 
, 
. Таким образом, уравнение эллипсоида принимает вид
. (8)
По условию точка принадлежит эллипсоиду, следовательно ее координаты удовлетворяют уравнению эллипсоида. Подставляя координаты точки M в уравнение (8), получаем
,
, 
.
Следовательно, искомое уравнение эллипсоида имеет вид
.
Ответ: .
Задача 2. Установить, что плоскость 
пересекает эллипсоид 
по эллипсу, найти его полуоси и вершины.
Координаты общих точек эллипсоида и плоскости удовлетворяют системе уравнений:
Выразив из первого уравнения z и подставив его во второе, получим
,
.
Последнее уравнение определяет в плоскости , эллипс, вершина которого лежит на оси Oz, большая полуось равна 
, а малая полуось – 
. Следовательно, вершины этого эллипса имеют координаты 
, 
, 
, 
.
V. Задачи для самостоятельного решения.
11. Написать каноническое уравнение эллипсоида, который:
а) проходит через точку 
и пересекает плоскость yOz по эллипсу 
;
б) проходит через точку 
и пересекает плоскость xOz по эллипсу 
;
в) проходит через точку 
и пересекает плоскость yOz по эллипсу 
;
г) пересекает плоскость yOz по эллипсу 
, а плоскость xOy по окружности 
.
д) пересекает плоскость xOz по эллипсу 
, а плоскость yOz по эллипсу .
12. Написать каноническое уравнение эллипсоида, проходящего через точки (2, 2, 4), (0, 0, 6), (2, 4, 2).
13. Исследовать методом сечений эллипсоид 
.
14. Установить, что плоскость 
пересекает эллипсоид 
по эллипсу, найти его полуоси и вершины.
15. Доказать, что эллипсоид 
имеет одну общую точку с плоскостью 
, и найти ее координаты.
16. Даны вершины эллипсоида 
и 
. Написать уравнение этого эллипсоида, зная, что плоскость yOz пересекает его по эллипсу 
.
I. Теоретические сведения.
1. Однополостный гиперболоид.
Определение. Однополостным гиперболоидом называется множество точек пространства, координаты которых в некоторой системе координат удовлетворяют следующему уравнению
. (1)
Уравнение (1) называется каноническим уравнением однополостного гиперболоида.
Из уравнения гиперболоида можно получить ряд свойств:
1) Однополостный гиперболоид фигура неограниченная.
2) Плоскости симметрии однополостного гиперболоида: xOy, yOz, xOz;
оси симметрии однополостного гиперболоида: Ox, Oy, Oz;
центр симметрии однополостного гиперболоида: начало координат.
3) Вершинами поверхности называются точки пересечения с осями симметрии. Вершины однополостного гиперболоида: (точки пересечения с осью Ox) , (точки пересечения с осью Oy), ось Oz однополостный гиперболоид не пересекает.
Исследование однополостного гиперболоида методом сечений.
1) Сечение плоскостью a, параллельной плоскости .
(2)
. (3)
Из уравнении (3) следует, что при всех значениях h сечением однополостного гиперболоида является эллипс.
2) Сечение плоскостью b, параллельной плоскости .
(4)
. (5)
а) Если , то линия пересечения гипербола, действительная ось которой параллельна оси Ох. В частности, если , то , и в сечении мы получаем гиперболу 
;
б) если , то линия пересечения гипербола, действительная ось которой параллельная оси Oz;
в) если , то линия пересечения пара действительных пересекающихся прямых.
3) Сечение плоскостью g, параллельной плоскости .
(6)
. (7)
а) Если , то линия пересечения гипербола, действительная ось которой параллельна оси Оy. В частности, если , то 
, и в сечении мы получаем гиперболу 
;
б) если , то линия пересечения гипербола, действительная ось которой параллельная оси Oz;
в) если , то линия пересечения пара действительных пересекающихся прямых.
2. Двуполостный гиперболоид.
Определение. Двуполостным гиперболоидом называется множество точек пространства, координаты которых в некоторой системе координат удовлетворяют следующему уравнению
. (8)
Уравнение (8) – каноническое уравнение двуполостного гиперболоида.
Из уравнения гиперболоида можно получить ряд свойств:
1) Внутри полосы, ограниченной плоскостями , точек гиперболоида нет;
3) Плоскости симметрии двуполостного гиперболоида: xOy, yOz, xOz;
оси симметрии двуполостного гиперболоида: Ox, Oy, Oz;
центр симметрии двуполостного гиперболоида: начало координат.
3) Вершины двуполостного гиперболоида: 
(точки пересечения с осью Oz), оси Ox и Oy двуполостный гиперболоид не пересекает.
Исследование двуполостного гиперболоида методом сечений.
1) Сечение плоскостью a, параллельной плоскости .
(9)
. (10)
а) Если , то линия пересечения мнимый эллипс;
б) если , то линия пересечения эллипс;
в) если , то линия пересечения пара мнимых пересекающихся прямых с действительной точкой пересечения.
2) Сечение плоскостью b, параллельной плоскости .
(11)
. (12)
При любом значении h получаем гиперболу с действительной осью параллельной оси Oz. В частности, если , то , и в сечении мы получаем гиперболу 
;
3) Сечение плоскостью g, параллельной плоскости .
(13)
. (14)
При любом значении h получаем гиперболу с действительной осью параллельной оси Oz. В частности, если , то , и в сечении мы получаем гиперболу 
.
1. Покажите, что координатные плоскости являются плоскостями симметрии однополостного (двуполостного) гиперболоида.
2. Покажите, что координатные оси являются осями симметрии однополостного (двуполостного) гиперболоида.
3. Покажите, что начало координат является центром симметрии однополостного (двуполостного) гиперболоида.
4. Найдите уравнение линии, образующейся при пересечении гиперболоида 
с плоскостью xOy.
5. Найдите уравнение линии, образующейся при пересечении гиперболоида 
с плоскостью xOz.
III. Основные типовые задачи.
1. Составление канонического уравнения гиперболоида.
2. Исследование сечений гиперболоида.
IV. Примеры решения задач.
Задача 1. Написать каноническое уравнение однополостного гиперболоида, если он пересекает плоскость xOy по эллипсу 
, а плоскость yOz по гиперболе 
.
Каноническое уравнение однополостного гиперболоида имеет вид . Уравнение плоскости xOy: z=0. Следовательно, уравнение линии пересечения плоскости и гиперболоида ищем как решение системы
Получаем уравнение эллипса, лежащего в плоскости xOy
.
По условию задачи этот эллипс задан уравнением 
. Значит, 
.
Проводя аналогичные рассуждения, можно получить уравнение гиперболу, получающейся в сечении гиперболоида с плоскостью yOz
.
По условию, это гипербола . Следовательно, 
.
Таким образом, искомое уравнение гиперболоида имеет вид
.
Ответ: .
Задача 2. Напишите уравнение плоскости, параллельной плоскости yOz и пересекающей однополостный гиперболоид 
по гиперболе, действительная полуось которой равна 1.
Уравнение плоскости параллельной плоскости yOz имеет вид x=h. Линия пересечения этой плоскости с гиперболоидом задается системой 
Откуда получаем уравнение
,
.
Последнее уравнение – это каноническое уравнение гиперболы, действительная полуось которой равна 
. По условию она равна 1.
,
,
,
.
Следовательно, искомая плоскость имеет уравнение 
.
Ответ: .
V. Задачи для самостоятельного решения.
1. Написать каноническое уравнение однополостного гиперболоида, если поверхность:
а) проходит через точку 
и пересекает плоскость xOz по гиперболе 
;
б) пересекает плоскость xOy по окружности 
, а плоскость xOz по гиперболе 
.
2. Написать уравнение двуполостного гиперболоида в канонической системе координат, если точки 
, 
и 
лежат на данной поверхности.
3. Найти множество точек, для каждой из которых мод, 3), (0, 0, –3) есть величина постоянная, равная 4.
4. Определите вид линии пересечения однополостного гиперболоида 
и плоскости 
.
5. Доказать, что двуполостный гиперболоид 
имеет одну общую точку с плоскостью 
, и найти ее координаты.
6. Найти точки пересечения поверхности 
и прямой 
.
Тема: Параболоиды.
Прямолинейные образующие поверхностей второго порядка
I. Теоретические сведения.
1. Эллиптический параболоид.
Определение. Эллиптическим параболоидом называется множество точек пространства, координаты которых в некоторой системе координат удовлетворяют следующему уравнению
. (1)
Уравнение (1) – каноническое уравнение эллиптического параболоида.
Из уравнения параболоида следует:
1) Все точки эллиптического параболоида лежат выше плоскости xOy;
2) Плоскости симметрии эллиптического параболоида: yOz, xOz;
ось симметрии эллиптического параболоида: Oz;
центра симметрии у эллиптического параболоида нет.
3) Вершина эллиптического параболоида: О(0; 0; 0) – начало координат.
Исследование эллиптического параболоида методом сечений.
1) Сечение плоскостью a, параллельной плоскости .
(2)
. (3)
а) Если 
, то линия пересечения эллипс;
б) если 
, то линия пересечения мнимый эллипс;
в) если , то линия пересечения пара мнимых пересекающихся прямых с действительной точкой пересечения.
2) Сечение плоскостью b, параллельной плоскости .
(4)
. (5)
При любом значении h получаем параболу, ось которой параллельна оси Oz, В частности, если , то , и в сечении мы получаем параболу 
;
3) Сечение плоскостью g, параллельной плоскости .
(6)
. (7)
При любом значении h получаем параболу, ось которой параллельна оси Oz, ветви направлены вверх. В частности, если , то , и в сечении мы получаем параболу 
.
2. Гиперболический параболоид.
Определение. Гиперболическим параболоидом называется множество точек пространства, координаты которых в некоторой системе координат удовлетворяют следующему уравнению
. (8)
Уравнение (8) – каноническое уравнение гиперболического параболоида.
Из уравнения параболоида следует:
1) Гиперболический параболоид поверхность неограниченная;
2) Плоскости симметрии гиперболического параболоида: yOz, xOz;
ось симметрии: Oz;
центра симметрии у гиперболического параболоида нет.
3) Вершина: О(0; 0; 0) – начало координат.
Исследование гиперболического параболоида методом сечений.
1) Сечение плоскостью a, параллельной плоскости .
(9)
. (10)
а) Если , то линия пересечения гипербола с действительной осью параллельной оси Ох;
б) если , то линия пересечения гипербола с действительной осью параллельной оси Oy;
в) если , то линия пересечения пара действительных пересекающихся прямых.
2) Сечение плоскостью b, параллельной плоскости .
(11)
. (12)
При любом значении h получаем параболу, ось которой параллельна оси Oz, В частности, если , то , и в сечении мы получаем параболу ;
3) Сечение плоскостью g, параллельной плоскости .
(13)
Или
. (14)
При любом значении h получаем параболу, ось которой параллельна оси Oz, ветви направлены вниз. В частности, если , то , и в сечении мы получаем параболу 
.
3. Прямолинейные образующие поверхностей второго порядка.
Определение. Прямая l называется прямолинейной образующей поверхности второго порядка, если каждая точка этой прямой лежит на поверхности.
Очевидно, что образующие конических и цилиндрических поверхностей являются прямолинейными образующими. Кроме того, прямолинейные образующие имеют однополостный гиперболоид и гиперболический параболоид. У однополостного гиперболоида и гиперболического параболоида существует два семейства прямолинейных образующих, таких что:
1) через каждую точку поверхности проходят по одной прямолинейной образующей из каждого семейства;
2) любые две прямолинейные образующие одного семейства являются скрещивающимися.
Прямолинейные образующие однополостного гиперболоида задаются следующими системами уравнений:
I. 
II. 
(15)
где k и l – любые числа.
Прямолинейные образующие гиперболического параболоида задаются следующими системами уравнений:
I. 
II. 
(16)
1) Докажите, что линией пересечения эллиптического параболоида 
и плоскости 
является эллипс, найдите его полуоси и вершину.
2) Покажите, что плоскость xOy не является плоскостью симметрии гиперболического параболоида.
3) Напишите каноническое уравнение гиперболического параболоида с вершиной в начале координат, ось которого совпадает с осью Oy.
4) Определите вид линии пересечения гиперболического параболоида 
и плоскости 
.
5) Сколько прямолинейных образующих проходит через каждую точку гиперболического параболоида, конуса, цилиндра, однополостного гиперболоида?
III. Основные типовые задачи.
1) Составление канонического уравнения параболоида.
2) Исследование параболоида методом сечений.
3) Составление уравнений прямолинейных образующих поверхностей второго порядка.
IV. Примеры решения задач.
Задача 1. Найти фигуру, состоящую из всех точек, одинаково удаленных от данной плоскости a и данной точки А, не лежащей в этой плоскости.
Обозначим расстояние между точкой А и плоскостью a через р. Введем в пространстве систему координат так, чтобы начало координат находилось посередине между точкой А и плоскостью a, плоскость xOy была параллельна плоскости a. Тогда точка А имеет координаты 
, а уравнение плоскости a имеет вид 
. Пусть точка 
произвольная точка, удовлетворяющая условию задачи. Тогда
,
.
По условию 
, следовательно, 
, т. е.
,
,
,
.
Таким образом, искомое множество точек есть эллиптический параболоид, заданный последним уравнением.
Ответ: .
Задача 2. Исследовать методом сечений поверхность 
.
Исследуем сечения гиперболического параболоида координатными плоскостями и плоскостями им параллельными.
1) Сечение плоскостью a, параллельной плоскости .
.
а) Если , то линия пересечения гипербола с действительной осью параллельной оси Ох;
б) если , то линия пересечения гипербола с действительной осью параллельной оси Oy;
в) если , то линия пересечения пара действительных пересекающихся прямых.
2) Сечение плоскостью b, параллельной плоскости .
.
При любом значении h получаем параболу, ось которой параллельна оси Oz, В частности, если , то , и в сечении мы получаем параболу 
;
3) Сечение плоскостью g, параллельной плоскости .
.
При любом значении h получаем параболу, ось которой параллельна оси Oz, ветви направлены вниз. В частности, если , то , и в сечении мы получаем параболу 
.
Задача 3. Написать уравнения двух систем прямолинейных образующих однополостного гиперболоида 
и определить те из них, которые проходят через точку 
.
Приведем уравнение гиперболоида к каноническому виду:
.
Перенесем второе слагаемое в правую часть
.
Применим формулу разности квадратов
.
Равенство имеет место в том случае, если множители в левой и правой частях пропорциональны
I. 
II.
Мы получили уравнения двух систем прямолинейных образующих однополостного гиперболоида. Теперь найдем те из них, которые проходят через данную точку . Подставим координаты точки в каждую из систем:
I. 
.
Подставляя это соотношение в систему I, получаем
– общие уравнения прямолинейной образующей.
I. 
.
Подставляем в II:
– общие уравнения прямолинейной образующей.
Ответ: и
V. Задачи для самостоятельного решения.
1) Найти уравнение параболоида с центром в начале координат, ось которого совпадает с осью Oz и который проходит через точки
(1; –2; 1) и (–3; –3; 2).
2) Дана плоскость a и перпендикулярная к ней прямая l. Найти множество точек пространства, для каждой из которых квадрат расстояния до прямой l в три раза больше расстояния до плоскости a.
3) Напишите каноническое уравнение гиперболического параболоида с вершиной в начале координат, ось которого совпадает с осью Oy, если известно, что он проходит через точки 
и 
.
4) Доказать, что эллиптический параболоид 
имеет одну общую точку с плоскостью 
, и найти ее координаты.
5) Найдите прямолинейные образующие параболоида 
, проходящие через точку М(2; 0; 1).
6) Убедившись, что точка А(–2; 0; 1) лежит на гиперболическом параболоиде 
, определить острый угол, образованный его прямолинейными образующими, проходящими через точку А.
7) Найдите прямолинейные образующие гиперболоида 
, проходящие через точку (6; 2; 8).
8) Найдите прямолинейные образующие гиперболоида 
, проходящие через точку (5; 3; 2).
9) На гиперболическом параболоиде 
найти прямолинейные образующие, параллельные плоскости 
.
10) Написать уравнение плоскости, параллельной плоскости 
и пересекающей параболоид 
по двум прямолинейным образующим. Найти уравнения этих образующих.
http://a-geometry.narod.ru/problems/problems_46.htm
http://pandia.ru/text/78/609/25488-7.php