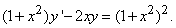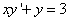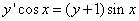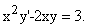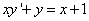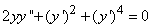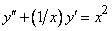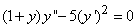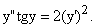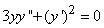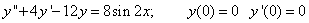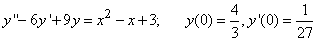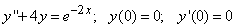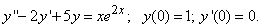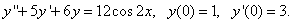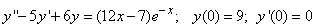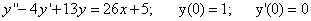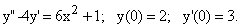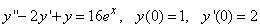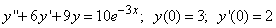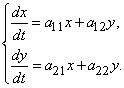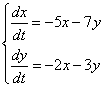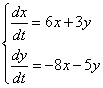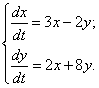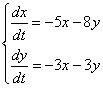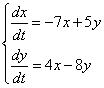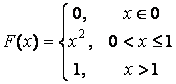Составить уравнение линии каждая точка которой находится
        Элементы векторной алгебры и аналитической геометрии.
        1-10.  Даны векторы   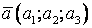
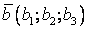
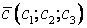
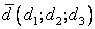
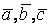
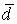
- 1. а(1;2;3), b(–1;3;2), c(7;–3;5). d(6;10;17).
- 2. а(4;7;8), b(9;1;3), c(2;–4;1). d(1;-13;-13).
- 3. а(8;2;3), b(4;6;10), c(3;–2;1). d(7;4;11).
- 4. а(10;3;1), b(1;4;2), c(3;9;2). d(19;30;7).
- 5. а(2;4;1), b(1;3;6), c(5;3;1). d(24;20;6).
- 6. а(1;7;3), b(3;4;2), c(4;8;5), d(7;32;14).
- 7. а(1;-2;3), b(4;7;2), c(6;4;2). d(14;18;6).
- 8. а(1;4;3), b(6;8;5), c(3;1;4). d(21;18;33).
- 9. а(2;7;3), b(3;1;8), c(2;-7;4), d(16;14;27).
- 10. а(7;2;1), b(4;3;5), c(3;4;-2), d(2;-5;-13).
        11-20.  Даны координаты вершин пирамиды   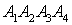
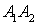
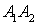
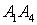
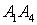
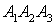
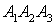
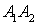
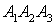
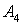
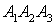
- 11. А1(4;2;5), А2(0;7;2), А3(0;2;7), А4(1;5;0).
- 12. А1(4;4;10), А2(4;10;2), А3(2;8;4), А4(9;6;4).
- 13. А1(4;6;5), А2(6;9;4), А3(2;10;10), А4(7;5;9).
- 14. А1(3;5;4), А2(8;7;4), А3(5;10;4), А4(4;7;8).
- 15. А1(10;6;6), А2(-2;8;2), А3(6;8;9), А4(7;10;3).
- 16. А1(1;8;2), А2(5;2;6), А3(5;7;4), А4(4;10;9).
- 17. А1(6;6;5), А2(4;9;5), А3(4;6;11), А4(6;9;3).
- 18. А1(7;2;2), А2(5;7;7), А3(5;3;1), А4(2;3;7).
- 19. А1(8;6;4), А2(10;5;5), А3(5;6;8), А4(8;10;7).
- 20. А1(7;7;3), А2(6;5;8), А3(3;5;8), А4(8;4;1).
- 21. Уравнение одной из сторон квадрата x+3y–5=0. Составить уравнения трех остальных сторон квадрата, если Р(–1;0) – точка пересечения его диагоналей. Сделать чертеж.
- 22. Даны уравнения одной из сторон ромба х–3у+10=0 и одной из его диагоналей х+4у–4=0; диагонали ромба пересекаются в точке Р(0;1). Найти уравнения остальных сторон ромба.
- 23. Уравнения двух сторон параллелограмма х+2у+2=0 и х+у–4=0, а уравнение одной из его диагоналей х–2=0. Найти координаты вершин параллелограмма.
- 24. Даны две вершины А(–3;3) и В(5;–1) и точка D(4;3) пересечения высот треугольника. Составить уравнения его сторон.
- 25. Даны вершины А(–3; –2), В(4; –1), С(1;3) трапеции ABCD (AD||BC). Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины D этой трапеции. Сделать чертёж.
- 26. Даны уравнения двух сторон треугольника 5х–4у+15=0 и 4х+у–9=0. Его медианы пересекаются в точке Р(0;2). Составить уравнение третьей стороны треугольника. Сделать чертеж.
- 27. Даны две вершины А(2;–2) и В(3;–1) и точка Р(1;0) пересечения медиан треугольника АВС. Составить уравнение высоты треугольника, проведенного через третью вершину С. Сделать чертеж.
- 28. Даны уравнения двух высот треугольника x+y=4 и y=2x и одна из его вершин А(0;2). Составить уравнения сторон треугольника.
- 29. Даны уравнения двух медиан треугольника х–2у+1=0 и у–1=0 и одна из его вершин (1;3). Составить уравнения его сторон.
- 30. Две стороны треугольника заданы уравнениями 5x–2y–8=0 и 3x–2y–8=0, а середина третьей стороны совпадает с началом координат. Составить уравнение этой стороны. Сделать чертёж.
- 31. Составить уравнение и построить линию, расстояния каждой точки которой от начала координат и от точки А(5;0) относится как 2:1.
- 32. Составить уравнение и построить линию, расстояние каждой точки которой от точки А(–1;0) вдвое меньше расстояния её от прямой х=–4.
- 33. Составить уравнение и построить линию, расстояние каждой точки которой от точки А(2;0) и от прямой 5х+8=0 относятся как 5:4.
- 34. Составить уравнение и построить линию, каждая точка которой находится вдвое дальше от точки А(4;0), чем от точки В(1;0).
- 35. Составить уравнение и построить линию, расстояние каждой точки которой от точки А(2;0) и от прямой 2х+5=0 относятся как 4:5.
- 36. Составить уравнение и построить линию, расстояние каждой точки которой от точки А(3;0) вдвое меньше расстояния от точки В(26;0).
- 37. Составить уравнение и построить линию, каждая точка которой одинаково удалена от точки А(0;2) и от прямой у–4=0.
- 38. Составить уравнение и построить линию, каждая точка которой равноотстоит от оси ординат и от окружности    
   .
Замечание. Напомним, что за расстояние от точки А до фигуры Ф принимается наименьшее из расстояний между точкой А и точками фигуры Ф. - 39. Составить уравнение линии, каждая точка которой равноудалена от точки А(2;6) и от прямой у+2=0.
- 40. Составить уравнение и построить линию, каждая точка которой отстоит от точки А(–4;0) втрое дальше, чем от начала координат.
        41-50.  Линия задана уравнением     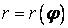
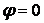
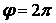
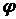
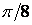
- 41.
       .
- 42.
       .
- 43.
       .
- 44.
       .
- 45.
       .
- 46.
       .
- 47.
       .
- 48.
       .
- 49.
       .
- 50.
       .
        Элементы линейной алгебры.
        51-60.   Дана система линейных уравнений 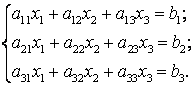
- 51.
- 52.
- 53.
- 54.
- 55.
- 56.
- 57.
- 58.
- 59.
- 60.
        61-70.   Даны два линейных преобразования 
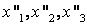
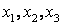
- 61.
- 62.
- 63.
- 64.
- 65.
- 66.
- 67.
- 68.
- 69.
- 70.
        71-80.   Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.
- 71.
- 72.
- 73.
- 74.
- 75.
- 76.
- 77.
- 78.
- 79.
- 80.
        81-90.   Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка.
- 81.
- 82.
- 83.
- 84.
- 85.
- 86.
- 87.
- 88.
- 89.
- 90.
        91-100.   Дано комплексное число     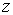
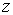
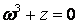
- 91.
- 92.
- 93.
- 94.
- 95.
- 96.
- 97.
- 98.
- 99.
- 100.
Введение в математический анализ.
- 101. Построить график функции y=Asin(ax+b) преобразованием графика функции y=sinx.
- 102. Построить график функции y=Asin(ax+b) преобразованием графика функции y=sinx.
- 103. Построить график функции y=Asin(ax+b) преобразованием графика функции y=sinx.
- 104. Построить график функции y=Asin(ax+b) преобразованием графика функции y=sinx.
- 105. Построить график функции y=Asin(ax+b) преобразованием графика функции y=sinx.
- 106. Построить график функции y=Acos(ax+b) преобразованием графика функции y=cosx.
- 107. Построить график функции y=Acos(ax+b) преобразованием графика функции y=cosx.
- 108. Построить график функции y=Acos(ax+b) преобразованием графика функции y=cosx.
- 109. Построить график функции y=Acos(ax+b) преобразованием графика функции y=cosx.
- 110. Построить график функции y=Acos(ax+b) преобразованием графика функции y=cosx.
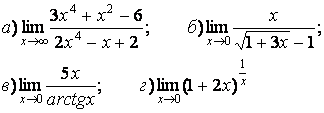
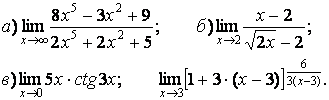
- 111. Найти пределы функций, не пользуясь правилом Лопиталя.
- 112. Найти пределы функций, не пользуясь правилом Лопиталя.
- 113. Найти пределы функций, не пользуясь правилом Лопиталя.
- 114. Найти пределы функций, не пользуясь правилом Лопиталя.
- 115. Найти пределы функций, не пользуясь правилом Лопиталя.
- 116. Найти пределы функций, не пользуясь правилом Лопиталя.
- 117. Найти пределы функций, не пользуясь правилом Лопиталя.
- 118. Найти пределы функций, не пользуясь правилом Лопиталя.
- 119. Найти пределы функций, не пользуясь правилом Лопиталя.
- 120. Найти пределы функций, не пользуясь правилом Лопиталя.
- 121. Заданы функция y=f(x) и два значения аргумента x1 и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти её пределы в точке разрыва слева и справа; 3) сделать схематический чертеж.
- 122. Заданы функция y=f(x) и два значения аргумента x1 и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти её пределы в точке разрыва слева и справа; 3) сделать схематический чертеж.
- 123. Заданы функция y=f(x) и два значения аргумента x1 и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти её пределы в точке разрыва слева и справа; 3) сделать схематический чертеж.
- 124. Заданы функция y=f(x) и два значения аргумента x1 и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти её пределы в точке разрыва слева и справа; 3) сделать схематический чертеж.
- 125. Заданы функция y=f(x) и два значения аргумента x1 и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти её пределы в точке разрыва слева и справа; 3) сделать схематический чертеж.
- 126. Заданы функция y=f(x) и два значения аргумента x1 и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти её пределы в точке разрыва слева и справа; 3) сделать схематический чертеж.
- 127. Заданы функция y=f(x) и два значения аргумента x1 и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти её пределы в точке разрыва слева и справа; 3) сделать схематический чертеж.
- 128. Заданы функция y=f(x) и два значения аргумента x1 и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти её пределы в точке разрыва слева и справа; 3) сделать схематический чертеж.
- 129. Заданы функция y=f(x) и два значения аргумента x1 и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти её пределы в точке разрыва слева и справа; 3) сделать схематический чертеж.
- 130. Заданы функция y=f(x) и два значения аргумента x1 и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти её пределы в точке разрыва слева и справа; 3) сделать схематический чертеж.
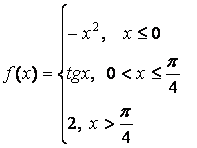
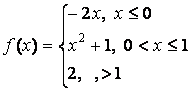
- 131. Задана функция y=f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
- 132. Задана функция y=f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
- 133. Задана функция y=f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
- 134. Задана функция y=f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
- 135. Задана функция y=f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
- 136. Задана функция y=f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
- 137. Задана функция y=f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
- 138. Задана функция y=f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
- 139. Задана функция y=f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
- 140. Задана функция y=f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
Производная и её приложения входят следующие задачи.
- 141-150. Найти производные dy/dx данных функций.
    141    142    143    144    145    146    147    148    149    150
151-160. Найти     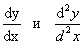
    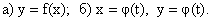
    151    152    153    154    155    156    157    158    159    160
161-170. Применяя формулу Тейлора с остаточным членом в форме Лагранжа к функции     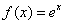
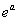
    161    162    163    164    165    166    167    168    169    170
171-180. Найти наибольшее и наименьшее значения функции y=f(x) на отрезке [a,b].
    171    172    173    174    175    176    177    178    179    180
Приложения дифференциального исчисления.
- 191-210. Исследовать методами дифференциального исчисления функцию y=f(x) и, используя результаты исследования, построить её график.
-     191.    
                       192.    
    193.     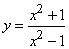
    195.     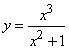
    197.     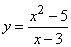
    199.     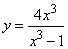
    201.     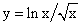
    203.     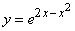
    205.     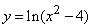
    207.     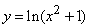
    209.     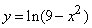
211-220. Найти уравнение касательной, уравнение нормальной плоскости и вычислить кривизну линии r=r(t) в точке t0.
    211    212    213    214    215    216    217    218    219    220
221-230. Определить количество действительных корней уравнения     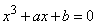
    221    222    223    224    225    226    227    228    229    230
Дифференциальное исчисление функции нескольких переменных.
        231-240.  Дана функция   .gif)
- 231.
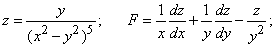
        241-250.  Даны функция   .gif)
.gif)
.gif)
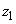
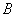
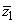
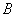
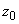
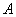
.gif)
.gif)
- 241.
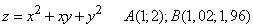
        251-260.  Найти наименьшее и наибольшее значения функции   .gif)
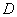
- 251.
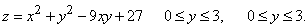
        261-270.  Даны функция   .gif)
.gif)
.gif)
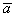
- 261.
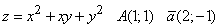
        271-280.   Экспериментально получены пять значений искомой функции   .gif)
Методом наименьших квадратов найти функцию   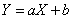
.gif)
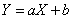
- 271.             y// 4,3 / 5,3 / 3,8 / 1,8 / 2,3
- 311.  Вычислить площадь фигуры, ограниченной параболой    
    и прямой y=3x+7.
- 312.  Вычислить площадь фигуры, ограниченной одной аркой циклоиды    
    и осью Ox.
- 313.  Вычислить площадь фигуры, ограниченной кардиоидой    
    .
- 314.  Вычислить площадь фигуры, ограниченной четырёхлепестковой розой    
    .
- 315.  Вычислить объём тела, образованного вращением вокруг оси Ox фигуры, ограниченной параболами    
   .
- 316.  Вычислить объём тела, образованного вращением вокруг оси Ox фигуры, ограниченной полуэллипсом    
   , параболой    
    и осью Oy.
- 317.  Вычислить объём тела, образованного вращением вокруг оси Oy фигуры, ограниченной кривыми
- 318.  Вычислить длину дуги полукубической параболы    
    от точки A(2;0) до точки B(6;8).
- 319.  Вычислить длину кардиоиды    
    .
- 320.  Вычислить длину одной арки циклоиды    
    .
Неопределённый и определённый интегралы.
- 281-290.  Найти неопределенные интегралы. В двух первых примерах (п.а и б) результаты проверить дифференцированием.
      281.     282.     283.    284.    285.     286.     287.     288.     289.     290.
291-300.  Вычислить приближенное значение определенного интеграла 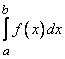
        291.     292.     293.    294.    295.     296.     297.     298.     299.     300.
301-310.  Вычислить несобственный интеграл или доказать его расходимость.
        301.     302.     303.    304.    305.     306.     307.     308.     309.     310.
«Дифференциальные уравнения».
- 321-340. Найти общее решение дифференциального уравнения.
-     321.    
                       322.    
    323.     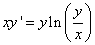
    325.     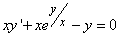
    327.     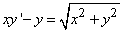
    329.     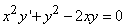
    331.     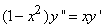
    333.     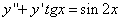
    335.     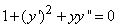
    337.     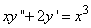
    339.     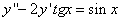
341-350. Найти частное решение дифференциального уравнения     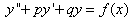
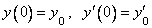
    341.    
    342.    
    343.    
    344.    
    345.    
    346.    
    347.    
    348.    
    349.    
    350.    
351-360. Дана система линейных дифференциальных уравнений с постоянными коэффициентами.
Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать в матричной форме данную систему и её решение.
    351.     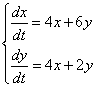
    353.     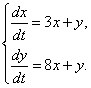
    355.     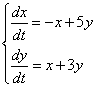
    357.     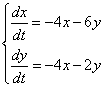
    359.     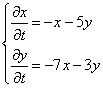
Кратные, криволинейные и поверхностные интегралы. Векторный анализ.
-       371-380.   Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а>0).
      371.     372.     373.    374.    375.     376.     377.     378.     379.     380.
      281-390.   Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость xОy.
      381.     382.     383.    384.    385.     386.     387.     388.     389.     390.
      391.   Вычислить криволинейный интеграл 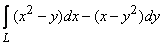
      392.   Вычислить криволинейный интеграл 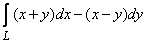
      393.   Вычислить криволинейный интеграл 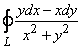
      394.   Вычислить криволинейный интеграл 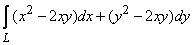
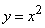
      395.   Вычислить криволинейный интеграл 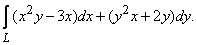
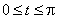
      396.   Вычислить криволинейный интеграл 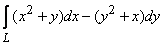
      397.   Вычислить криволинейный интеграл 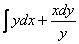
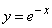
      398.   Вычислить криволинейный интеграл 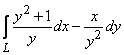
      399.   Вычислить криволинейный интеграл 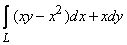
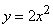
      400.   Вычислить криволинейный интеграл 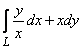
      401-410.   Даны векторное поле F=Xi+Yj+Zk и плоскость Ax+By+Cz+D=0 (р), которая совместно с координатными плоскостями образует пирамиду V. Пусть   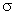
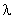
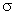
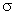
      1) поток векторного поля F через поверхность   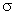
    2) циркуляцию векторного поля F по замкнутому контуру   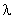
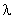
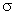
    3) поток векторного поля F через полную поверхность пирамиды V в направлении внешней нормали к её поверхности непосредственно и применив теорему Остроградского. Сделать чертеж.
      401.     402.     403.    404.    405.     406.     407.     408.     409.     410.
      411-420.   Проверить, является ли векторное поле F=Xi+Yj+Zk потенциальным и соленоидальным. В случае потенциальности поля F найти его потенциал.
      411.     412.     413.    414.    415.     416.     417.     418.     419.     420.
-       421-430.   Исследовать сходимость ряда    
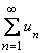     .
    .      421.     422.     423.    424.    425.     426.     427.     428.     429.     430.
      431-440.   Найти интервал сходимости степенного ряда     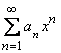
      431.     432.     433.    434.    435.     436.     437.     438.     439.     440.
      441-450.   Вычислить определенный интеграл     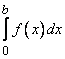
      441.     442.     443.    444.    445.     446.     447.     448.     449.     450.
      451-460.   Найти три первых отличных от нуля члена разложения в степенной ряд решения     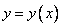
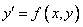
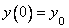
      451.     452.     453.    454.    455.     456.     457.     458.     459.     460.
      451.     462.     463.    464.    465.     466.     467.     468.     469.     470.
Уравнения математической физики. Функции комплексного переменного. Операционное исчисление.
-       471-480.   Методом Даламбера найти уравнение u=u(x;t) формы однородной бесконечной струны, определяемой волновым уравнением    
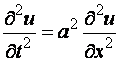    , если в начальный момент    
   , если в начальный момент          форма струны и скорость точки струны с абсциссой х определяется соответственно заданными функциями
    форма струны и скорость точки струны с абсциссой х определяется соответственно заданными функциями 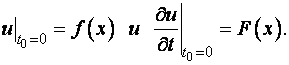
      471.     472.     473.    474.    475.     476.     477.     478.     479.     480.
      481-490.   Представить заданную функцию W=f(z), где z=x+iy, в виде W=u(x,y)+iv(x,y); проверить, является ли она аналитической. Если да, то найти значение её производной в заданной точке     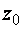
      481.     482.     483.    484.    485.     486.     487.     488.     489.     490.
      491-500.   Разложить функцию f(z) в ряд Лорана в окрестности точки     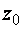
      491.     492.     493.    494.    495.     496.     497.     498.     499.     500.
      501-510.   Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям.
      501.     502.     503.    504.    505.     506.     507.     508.     459.     510.
      511-520.   Методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее начальным условиям.
      511.     512.     513.    514.    515.     516.     517.     518.     519.     520.
531-540. Дискретная случайная величина Х может принимать только два значения: х1 и х2, причем х1 меньше x2. Известны вероятность р1 возможного значения х1, математическое ожидание М(х) и дисперсия D(x). Найти закон распределения этой случайной величины.
- 531.   p1=0,1; M(x)=3,9; D(x)=0,09
- 532.   p1=0,3; M(x)=3,7; D(x)=0,21
- 533.   p1=0,5; M(x)=3,5; D(x)=0,25
- 534.   p1=0,7; M(x)=3,3; D(x)=0,21
- 535.   p1=0,9; M(x)=3,1; D(x)=0,09
- 536.   p1=0,9; M(x)=2,2; D(x)=0,36
- 537.   p1=0,8; M(x)=3,2; D(x)=0,16
- 538.   p1=0,6; M(x)=3,4; D(x)=0,24
- 539.   p1=0,4; M(x)=3,6; D(x)=0,24
- 540.   p1=0,2; M(x)=3,8; D(x)=0,16
541-540. Случайная величина Х задана функцией распределения F(x). Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины.
- 541.
551-560. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины x. Найти вероятность попадания этой величины в заданный интервал (α, β)
- 551.   a=10, σ=4, α=2, β=13.
561-570. Задана матрица Р1 вероятностей перехода цепи Маркова из состояния i (i=1,2) в состояние j (j=1,2) за один шаг. Найти матрицу Р2 перехода из состояния i в состояние j за два шага
- 561.
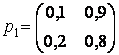
571-580. Найти доверительный интервал для оценки математического ожидания а нормального распределения с надежностью 0,95, зная выборочную среднюю     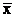
- 571.    
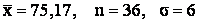
Составить уравнение линии каждая точка которой находится
Linker1989
Я не понимаю.
Посмотрите, что я написала выше. Прочтите это внимательно
Расстояние от точки М(х,у) до прямой у+2=0 равно |y+2|
не у+4. Это неверно. А |y+2|. Посмотрите формулу расстояния от точки до прямой
Скачайте книгу Соболь Практикум по высшей математике
Руководства по решению задач («Решебники» по высшей математике)
Расстояние от М(х,у) до точки (2,6) равно корню квадратному из (x-2)^2+(y-6)^2
А теперь вы это приравниваете и возводите в квадрат.
а что значит в каноническом виде
Как можно решать задачи по ангему, не зная определений и формул?
Скачайте книгу и скачайте еще Бортаковский Аналитическая геометрия в примерах и задачах.
И прочтите про канонические уравнения и как строят параболу
В принципе у Соболя это есть
http://diary.ru/~eek/p83205109.htm
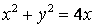    .
   .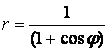 .
.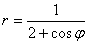 .
.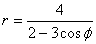 .
.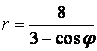 .
.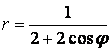 .
.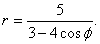 .
.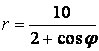 .
.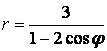 .
.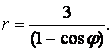 .
.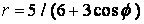 .
.
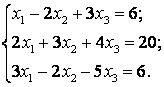
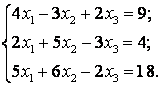


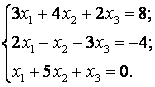

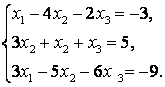
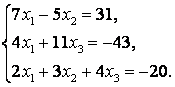
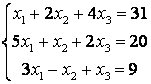


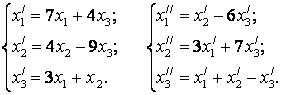
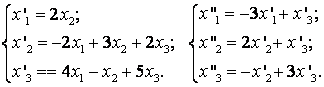

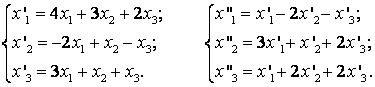


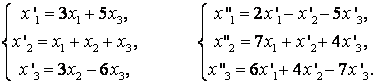
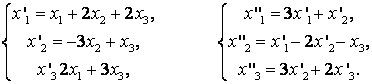

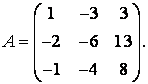

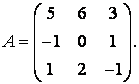
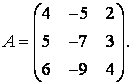
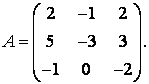
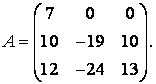

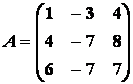
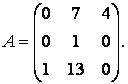
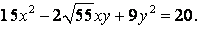
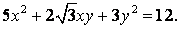
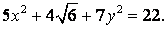
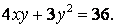
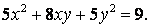
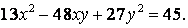
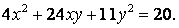
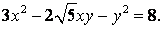
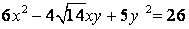
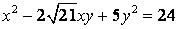
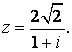
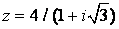
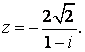
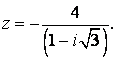
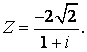
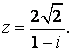
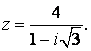
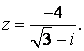
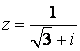
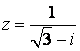
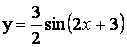
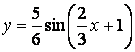
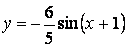
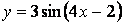
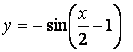
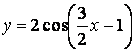
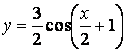
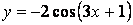
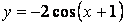
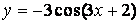

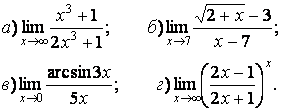
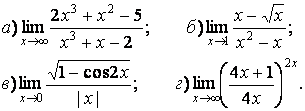
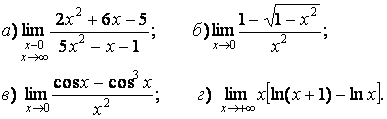
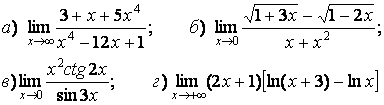
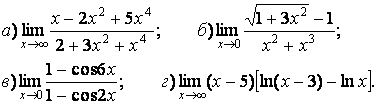
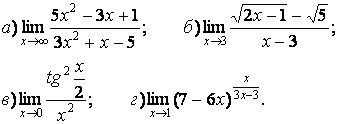
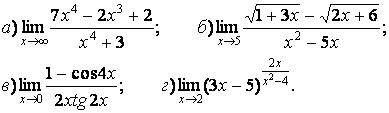

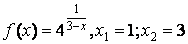
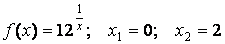
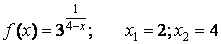
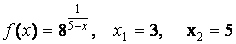
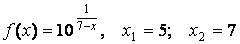
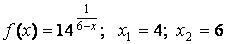
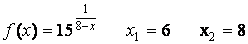
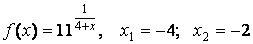
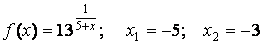

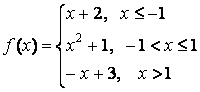
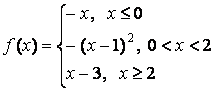


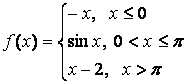
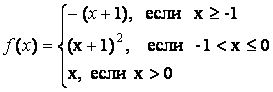
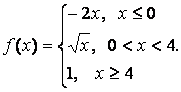
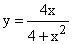                        192.    
                       192.     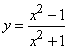
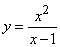
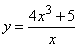
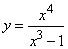
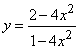
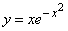
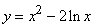
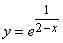
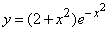
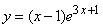
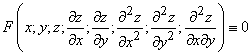
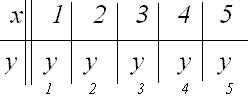
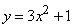     и прямой y=3x+7.
    и прямой y=3x+7.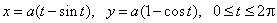     и осью Ox.
    и осью Ox.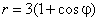     .
    .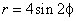     .
    .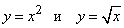    .
   .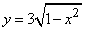    , параболой    
   , параболой     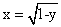     и осью Oy.
    и осью Oy.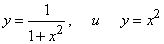
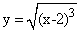     от точки A(2;0) до точки B(6;8).
    от точки A(2;0) до точки B(6;8).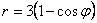     .
    .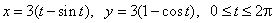     .
    .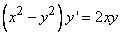                        322.    
                       322.