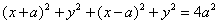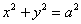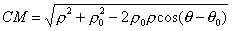Контрольная работа. Выполним
Задача 2. Составить уравнение линии, для каждой точки которой отношение расстояний до точки А (3; 0) и до прямой х=12 равно числу
=0,5. Полученное уравнение привести к простейшему виду и построить кривую.
Решение. Пусть М (х; у) – текущая (произвольная) точка искомого геометрического множества точек. Опустим перпендикуляр МВ на прямую х=12 (рис. 2). Тогда В (12; у). По условию задачи
МА= 


4х2 – 24х + 36 + 4у2 =х2 – 24х +144, 3х2 + 4у2=108,
Полученное уравнение представляет собой эллипс вида 

Определим фокусы эллипса F1 (−с; 0) и F2(с; 0). Для эллипса справедливо равенство b2=a2 – b2 =9 и с=3.
То есть, F1 ( −3; 0) и F2 (3; 0) – фокусы эллипса (точки F2 и А совпадают).
Эксцентриситет эллипса 
Задача 3. Составить уравнения линии, для каждой точки которой ее расстояние до точки А (3; −4) равно расстоянию до прямой у=2. Полученное уравнение привести к простейшему виду и построить кривую.
Решение. М (х; у) – текущая точка искомой кривой. Опустим из точки М перпендикуляр МВ на прямую у=2 (рис. 3). Тогда В (х; 2). Так как МА =МВ,
то 

(х – 3)2 +у2+8у+16 =у2 – 4у +4,
у +1= −
Полученное уравнение определяет параболу с вершиной в точке О’ (3; −1). Для приведения уравнения параболы к простейшему (каноническому) виду положим х – 3=Х’, у +1=У’. Тогда в системе координат Х’О’У’ уравнение параболы принимает следующий вид: У’=−
Вопросы для самопроверки
Дайте определение прямоугольной декартовой системы координат.
Напишите формулу для нахождения расстояния между двумя точками.
Напишите формулы для определения координат точки, делящей данный отрезок в данном отношении.
Напишите формулы преобразования координат: а) при параллельном переносе системы координат; б) при повороте системы координат.
Напишите уравнения прямой: а) с угловым коэффициентом; б) проходящей через данную точку в данном направлении; в) проходящей через две данные точки; г) в «отрезках».
Как найти координаты точки пересечения двух прямых?
Напишите формулу для определения угла между двумя прямыми.
Каковы условия параллельности и перпендикулярности двух прямых?
Сформулируйте определение окружности.
Напишите уравнение окружности с центром в любой точке плоскости хОу; с центром в начале координат.
Дайте определение эллипса. Напишите каноническое уравнение эллипса.
Что называется эксцентриситетом эллипса? Как изменяется форма эллипса с изменением эксцентриситета гиперболы.
Дайте определение гиперболы. Напишите каноническое уравнение гиперболы.
Напишите формулу для определения эксцентриситета гиперболы. Напишите уравнения для нахождения асимптот гиперболы.
Сформулируйте определение параболы. Напишите каноническое уравнение параболы, симметричной относительно оси Оу.
2.2. Кривые второго порядка на плоскости
2.2.1. Составить уравнение линии, для каждой точки которой отношение расстояния до точки F (2; 4) к расстоянию до прямой / : х = -4 равно 2. Привести уравнение линии к каноническому виду и определить вид этой кривой.
Решение. Пусть M (х; у) — текущая точка линии. Из точки M опускаем перпендикуляр на прямую х = -4, которыйпересекается с ней в точке N (-4; у). По условию задачи:
Возводя в квадрат, раскрывая скобки и делая приведение подобных членов, получаем:
Коэффициент при х2 делаем равным единице, для чего все уравнение делим на 3:
Многочлен, зависящий от х, записываем как полный квадрат: 
или, деля на 16, имеем:
Вводя новую систему координат:
приведем уравнение линии к каноническому виду:

Это есть каноническое уравнение гиперболы. m
Замечание. Если — = 1, то придем к каноническому уравнению n
параболы ‘
Составить уравнение линии отношение расстояний
Глава 10. Вывод уравнений заранее данных линий
В задачах предыдущего параграфа линия определялась при помощи данного уравнения. Здесь мы будем иметь задачи противоположного характера; в каждой из них линия определяется чисто геометрически, а уравнение ее требуется найти.
ПРИМЕР 1. В декартовой прямоугольной системе координат вывести уравнение геометрического места точек, сумма квадратов расстояний которых до двух данных точек 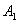
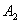
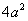
РЕШЕНИЕ. Обозначим буквой М произвольную точку линии, буквами х и у обозначим координаты этой точки. Так как точка М может занимать на линии любое положение то х и у являются переменными величинами; их называют текущими координатами.
Запишем геометрическое свойство линии символически:
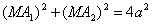
В этом отношении при движении точки М могут меняться длины 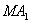
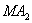
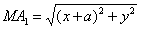
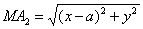
Подставив полученные выражения в равенство (1), найдем уравнение, связывающее координаты х, у точки М:
Это и есть уравнение данной линии.
Действительно, для каждой точки М, лежающей на этой инии, выполняется условие (1) и, следовательно, координаты точки М будут удовлетворять уравнению (2); для каждой точки М, не лежащей на линии, не будет выполняться условие (1) и, следовательно, ее координаты не будут удовлетворять уравнению (2).
Таким образом, задача решена. Однако уравнение (2) можно упростить; раскрывая скобки и приводя подобные члены, получим уравнение данной линии в виде:
Теперь легко понять, что данная линия есть окружность с центром в начале координат и радиусом, равным а.
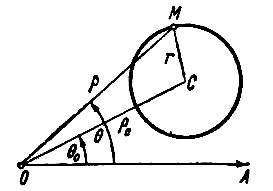
ПРИМЕР 2. В полярной системе координат вывести уравнение окружности, которая имеет центр С( 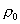
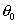
РЕШЕНИЕ. Олозначим буквой М произвольную точку окружности, буквами 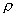
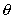
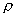
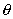
Все точки окружности отстоят от центра на расстоянии r ; запишем это условие символически:
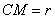
Выразим СМ через текущие координаты точки М (воспользуемся теоремой косинусов):
Подставив полученное выражение в равенство (1), найдем уравнение, связывающее координаты 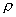
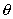
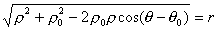
Это и есть уравнение данной окружности.
Действительно, для каждой точки М, лежащей на данной окружности, выполняется условие (1) и , следовательно, координаты точки М будут удовлетворять уравнению (2); для каждой точки М, не лежащей на данной окружности, не будет выполняться условие (1) и, следовательно, ее координаты не будут удовлетворять уравнению (2).
Таким образом, задача решена. Можно лишь несколько упростить полученное уравнение и представить его в виде, свободным от радикала:
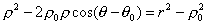
http://matica.org.ua/metodichki-i-knigi-po-matematike/a-s-shapkin-zadachi-po-vysshei-matematike-teorii-veroiatnostei-matematicheskoi-statistike-matematicheskomu-programmirovaniiu-s-resheniiami/2-2-krivye-vtorogo-poriadka-na-ploskosti
http://a-geometry.narod.ru/problems/problems_10.htm