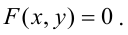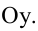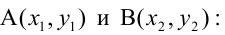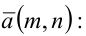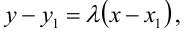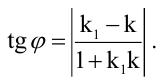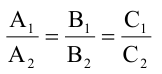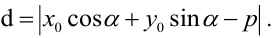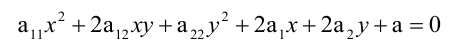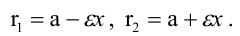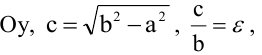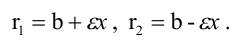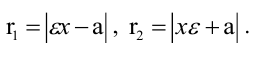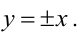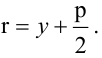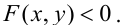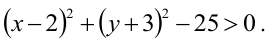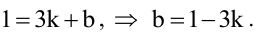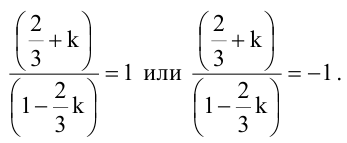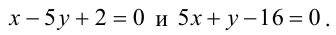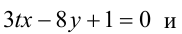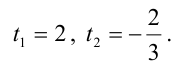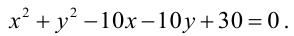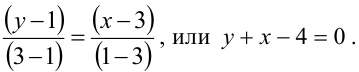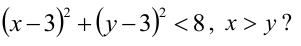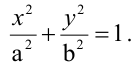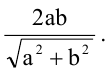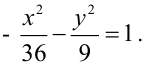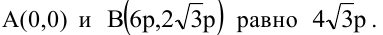Задачи для самостоятельного решения. 1 Составить уравнение хорды окружности х2+у2 = 49, делящейся в точке А(1;2) пополам
1 Составить уравнение хорды окружности х 2 +у 2 = 49, делящейся в точке А(1;2) пополам.
Ответ.х + 2у -5 = 0.
2. Определить координаты центров и радиусы окружностей:
Ответ: а) а = 4, b=-3, r= 5; б) а = -5, b = 2, r=0. Уравнение определяет точку;
в) а =2, b=-7, r 2 =-1. Уравнение не имеет геометрического смысла (мнимая, окружность).
3. Найти угол между радиусами окружности
х 2 +у 2 +4х-6у=0, проведенными в точки пересечения ее с осью Оу.
Ответ: tgφ=-2,4.
4. Составить уравнение окружности, проходящей через точки А(1; 2), В(0;-1), С(-3; 0).
Ответ: (х+1) 2 +(у -1) 2 =5.
5. Составить уравнение окружности, проходящей через точки А (7; 7) и В(-2; 4), зная, что ее центр лежит на прямой
Ответ: (х— З) 2 +(у-4) 2 =25.
6. Составить уравнение общей хорды окружностей х 2 +у 2 =16 и (х -5) 2 + у 2 = 9.
Ответ: х=3,2.
7. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса 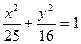
Ответ: 4х+3у+12= 0.
8. На прямой х+5=0 найти точку, одинаково удаленную от левого фокуса и верхней вершины эллипса 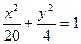
Ответ: М(—5; 7).
9. Пользуясь определением эллипса, составить его уравнение, зная, что точки F1 (0; 0) и F2 (1; 1) являются фокусами эллипса, а длина большой оси равна 2.
Ответ: Зх 2 + Зу 2 — 2ху — 2х — 2у — 1 == 0.
10. Составить уравнение геометрического места точек, расстояния которых от точки А (0; 1) з два раза меньше расстояния до прямой у—4=0.
Ответ: 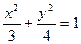
Занятие 16. Кривые второго порядка: гипербола, парабола
Гипербола.
Гиперболой называется геометрическое место точек, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (её обозначают через 2а), причем эта постоянная меньше расстояния между фокусами. Поместив фокусы гиперболы в точках F1(с; 0) и F2(-с;0), получаем уравнение гиперболы в виде 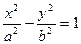

это простейшее (каноническое) уравнение гиперболы. Гипербола состоит из двух ветвей и расположена симметрично относительно осей координат. Точки А1(а;0) и А2(-а;0) называются вершинами гиперболы.
Отрезок А1А2=2а называют вещественной осью гиперболы, а отрезок В1В2=2b – мнимой осью (рис. 15).
Прямая называется асимптотой гиперболы, если расстояние точки гиперболы М (х;у) от этой прямой стремится к нулю при х→+∞ или х→-∞. Гипербола имеет две асимптоты, уравнения которых 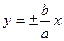
х = — а, у=b, у=-b. Прямые, проходящие через противоположные вершины этого прямоугольника, являются асимптотами гиперболы. На чертеже указано взаимное расположение гиперболы и ее асимптот. Отношение ε 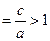
Если а=b, то уравнение гиперболы принимает вид
Такая гипербола называется равнобочной.

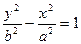
также является уравнением гиперболы, но вещественной осью этой гиперболы служит отрезок оси Оу длины 2b.
Две гиперболы 
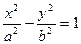
Пример 16.1.Эксцентриситет гиперболы равен 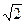
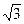
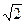
Решение. По определению эксцентриситета можем написать равенство 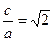
Другое равенство имеем из условия нахождения точки М на гиперболе, т. е. 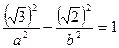
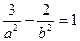
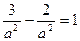
Таким образом, уравнение искомой гиперболы имеет вид х 2 — у 2 =1.
Парабола.
Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Если директрисой параболы 
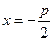
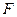
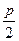

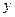

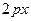
Эта парабола расположена симметрично относительно оси абсцисс (рис.6, где р 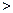
Уравнение

является уравнение параболы, симметричной относительно оси ординат. При p>0 параболы (16.1) и (16.2) обращены в положительную сторону соответствующей оси, а при p
Решение. Поскольку известны длина хорды и расстояние ее от вершины, то, следовательно , известны координаты конца этой хорды-точки М, лежащей на параболе. Уравнение параболы имеет вид 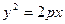

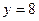
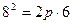

Таким образом, уравнение искомой параболы 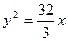
Пример 16.3. Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и отсекающей на биссектрисе 

Решение. Искомое уравнение параболы 

Длина хорды определяется как расстояние между двумя точками 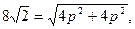
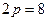

Геометрические свойства линий второго порядка
Окружность
определяет окружность радиуса R с центром C(a; B).
Если центр окружности совпадает с началом координат, то есть если a=0, B=0, то уравнение (1) принимает вид
ЗАДАЧА 3704 Точка С(3; -1) является центром
Эллипс
Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами. Постоянную сумму расстояний произвольной точки эллипса до фокусов принято обозначать через 2а. Фокусы эллипса обозначают буквами F1 и F2 , расстояние между ними — через 2с. По определению эллипса 2a>2c или a>c.
Пусть дан эллипс. Если оси декартовой прямоугольной системы координат выбраны так, что фокусы данного эллипса располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение данного эллипса имеет вид
где b=sqrt(a^2-c^2); очевидно, a>b. Уравнение вида (1) называется каноническим уравнением эллипса.
При указанном выборе системы координат оси координат являются осями симметрии эллипса, а начало координат — его центром симметрии (рис.). Оси симметрии эллипса называются просто его осями, центр симметрии — просто центром. Точки, в которых эллипс пересекает свои оси, называются его вершинами. На рис. Вершины эллипса ABCD точки A’, A, B’, B. Часто осями эллипса называются также отрезки A’A=2a и B’B=2b; вместе с тем отрезок ОА=а называют большой полуосью эллипса, отрезок OB=b — малой полуосью.
Если фокусы эллипса расположены на оси Оу (симметрично относительно начала координат), то уравнение эллипса имеет тот же вид (1), но в этом случае b>a; следовательно, если мы желаем буквой а обозначать большую полуось, то в уравнении (1) нужно буквы а и b поменять местами. Однако для удобства формулировок задач мы условимся буквой а всегда обозначать полуось, расположенную на оси Ох, буквой b — полуось, расположенную на оси Оу, независимо от того, что больше, a или b. Если a=b, то уравнение (1) определяет окружность, рассматриваемую как частный случай эллипса.
где а — большая полуось, называется эксцентриситетом эллипса. Очевидно, ε F1M=r1 и F2M=r2 (рис.) называются фокальными радиусами точки М. Фокальные радиусы могут быть вычислены по формулам
Если эллипс определен уравнением (1) и a>b, то прямые
называются директрисами эллипса (если b>a, то директрисы определяются уравнениями y=-b/ε, y=b/ε)
Каждая директриса обладает следующим свойством: если r — расстояние от произвольной точки эллипса до некоторого фокуса, d — расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r/d есть постоянная величина, равная эксцентриситету эллипса:
ЗАДАЧА 3705 Эксцентриситет эллипса e=2/3, фокальный
ЗАДАЧА 3706 Эксцентриситет эллипса e=2/5, расстояние
Гипербола
где b=sqrt(c^2 — a^2) . Уравнение вида (1) называется каноническим уравнением гиперболы. При указанном выборе системы координат оси координат являются осями симметрии гиперболы, а начало координат — ее центром симметрии (рис.). Оси симметрии гиперболы называются просто ее осями, центр симметрии — центром гиперболы. Гипербола пересекает одну из своих осей; точки пересечения называются вершинами гиперболы. На рис. Вершины гиперболы ABCD точки А’ и А.
Прямоугольник со сторонами 2а и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником гиперболы.
Отрезки длиной 2a и 2b, соединяющие середины сторон основного прямоугольника гиперболы, также называют ее осями. Диагонали основного прямоугольника (неограниченно продолженного) являются асимптотами гиперболы, их уравнения суть
определяет гиперболу, симметричную относительно координатных осей, с фокусами на оси ординат; уравнение (2), как и уравнение (1), называется каноническим уравнением гиперболы; в этом случае постоянная разность расстояний от произвольной точки гиперболы до фокусов равна 2b.
Две гиперболы, которые определяются уравнениями
в одной и той же системе координат, называются сопряженными.
Гипербола с равными полуосями (a=b) называется равносторонней; ее каноническое уравнение имеет вид
где а — расстояние от центра гиперболы до ее вершины, называется эксцентриситетом гиперболы. Очевидно, для любой гиперболы ε > 1. Если М(x; y) — произвольная точка гиперболы, то отрезки F1M и F2M (см. рис.) называются фокальными радиусами точки М. Фокальные радиусы точек правой ветви гиперболы вычисляются по формулам
фокальные радиусы точек левой ветви — по формулам
Если гипербола задана уравнением (1), то прямые, определяемые уравнениями
называются ее директрисами (см. рис.). Если гипербола задана уравнением (2), то директрисы определяются уравнениями
Каждая директриса обладает следующим свойством: если r — расстояние от произвольной точки гиперболы до некоторого фокуса, d — расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r/d есть постоянная величина, равная эксцентрисистету гиперболы:
ЗАДАЧА 3707 Эксцентриситет гиперболы e=2, фокальный
ЗАДАЧА 3708 Эксцентриситет гиперболы e=3/2, центр ее
Парабола
Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F, расстояние от фокуса до директрисы — буквой р. Число р называется параметром параболы.
Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение
Фокальный радиус произвольной точки М(x; y) параболы (то есть длина отрезка F(M) может быть вычислен по формуле
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параболы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.
Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение
если она лежит в верхней полуплоскости (рис.), и
если в нижней полуплоскости (рис.)
Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.
ЗАДАЧА 3709 Вычислить фокальный радиус точки М
ЗАДАЧА 3710 Составить уравнение параболы, если даны
Полярное уравнение эллипса, гиперболы, параболы
Полярное уравнение, общее по форме для эллипса, одной ветви гиперболы и параболы, имеет вид
где p, θ — полярные координаты произвольной точки линии, р — фокальный параметр (половина фокальной хорды линии, перпендикулярной к ее оси), ε — эксцентриситет (в случае параболы ε = 1). Полярная система координат при этом выбрана так, что полюс находится в фокусе, а полярная ось направлена по оси линии в сторону, противоположную ближайшей к этому фокусу директрисы.
ЗАДАЧА 3711 Дано уравнение эллипса x^2/a^2 + y^2/b^2
ЗАДАЧА 3712 Дано уравнение гиперболы x^2/a^2 —
ЗАДАЧА 3713 Дано уравнение параболы y^2 = 2px.
Составить уравнение общей хорды параболы и окружности
Уравнения прямых и кривых на плоскости с примерами решения
Содержание:
Уравнения прямых и кривых на плоскости
Уравнения кривых в большом количестве встречаются при чтении экономической литературы. Укажем некоторые из этих кривых.
Кривая безразличия — кривая, показывающая различные комбинации двух продуктов, имеющих одинаковое потребительское значение, или полезность, для потребителя.
Кривая потребительского бюджета — кривая, показывающая различные комбинации количеств двух товаров, которые потребитель может купить при данном уровне его денежного дохода.
Кривая производственных возможностей — кривая, показывающая различные комбинации двух товаров или услуг, которые могут быть произведены в условиях полной занятости и полного объема производства в экономике с постоянными запасами ресурсов и неизменной технологией.
Кривая инвестиционного спроса — кривая, показывающая динамику процентной ставки и объем инвестиций при разных процентных ставках.
Кривая Филлипса — кривая, показывающая существование устойчивой связи между уровнем безработицы и уровнем инфляции.
Кривая Лаффера — кривая, показывающая связь между ставками налогов и налоговыми поступлениями, выявляющая такую налоговую ставку, при которой налоговые поступления достигают максимума.
Уже простое перечисление терминов показывает, как важно для экономистов умение строить графики и анализировать уравнения кривых, каковыми являются прямые линии и кривые второго порядка — окружность, эллипс, гипербола, парабола. Кроме того, при решении большого класса задач требуется выделить на плоскости область, ограниченную какими-либо кривыми, уравнения которых заданы. Чаще всего эти задачи формулируются так: найти наилучший план производства при заданных ресурсах. Задание ресурсов имеет обычно вид неравенств, уравнения которых даны. Поэтому приходится искать наибольшее или наименьшее значения, принимаемые некоторой функцией в области, заданной уравнениями системы неравенств.
В аналитической геометрии линия на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению
Пусть на плоскости задана прямоугольная декартова система координат. Прямая на плоскости может быть задана одним из уравнений:
1. Общее уравнение прямой:
Вектор 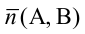
2. Уравнение прямой с угловым коэффициентом:
где 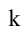
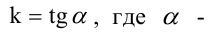
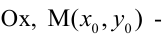
Уравнение (2.2) принимает вид 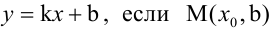
3. Уравнение прямой в отрезках:
где а и b — величины отрезков, отсекаемых прямой на осях координат.
4. Уравнение прямой, проходящей через две данные точки —
5. Уравнение прямой, проходящей через данную точку 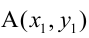
6. Нормальное уравнение прямой:
где 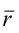
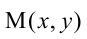
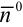
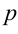
Нормальное уравнение прямой в координатной форме имеет вид:
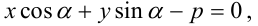
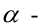
Уравнение пучка прямых с центром в точке 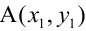
где 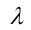
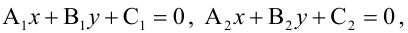
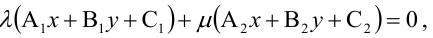
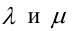
Величина угла между прямыми 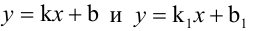
Равенство 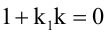
Для того, чтобы два уравнения

Уравнения (2.7), (2.8) задают две различные параллельные прямые, если 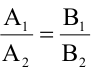
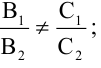
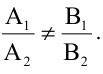
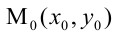
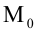
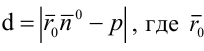
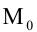
Общее уравнение кривой второго порядка имеет вид:
Предполагается, что среди коэффициентов уравнения 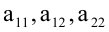
Уравнение окружности с центром в точке 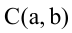

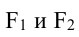
Эллипс, заданный уравнением (2.10), симметричен относительно осей координат.
Параметры а и b называются полуосями эллипса.
Пусть 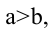
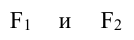
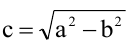
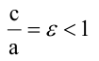
Расстояния от точки 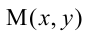
Если же 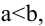
Если а=b, то эллипс является окружностью с центром в начале координат радиуса а.
Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных точек 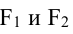
Каноническое уравнение гиперболы:
Гипербола, заданная уравнением (2.11), симметрична относительно осей координат. Она пересекает ось 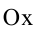
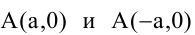
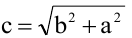
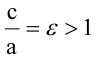
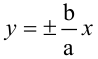
Расстояния от точки 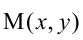
Гипербола, у которой а=b, называется равносторонней, ее уравнение 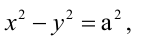
Гиперболы 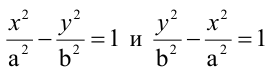
Каноническое уравнение параболы имеет два вида:
1. 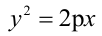
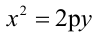
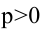
Парабола, уравнение которой 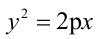
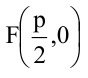
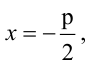
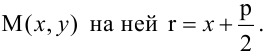
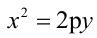
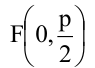
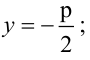
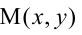
Уравнение 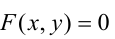
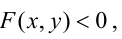
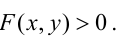
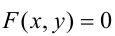
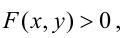
Прямая, уравнение которой 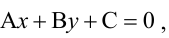
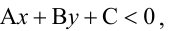
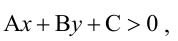
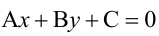
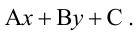
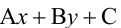
Точно так же решаются и нелинейные неравенства с двумя неизвестными.
Например, решим неравенство 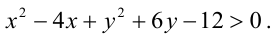
Уравнение 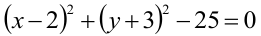
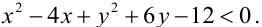
Пример:
Составьте уравнения прямых, проходящих через точку А(3,1) и наклоненных к прямой 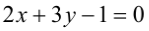
Решение:
Будем искать уравнение прямой в виде 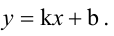
Величина угла между прямыми 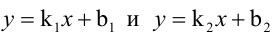
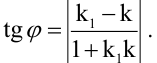
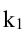
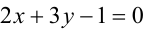
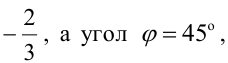
Имеем два значения 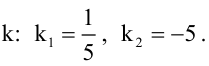
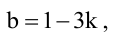
Пример:
При каком значении параметра t прямые, уравнения которых 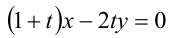
Решение:
Прямые, заданные общими уравнениями, параллельны, если коэффициенты при x и y пропорциональны, т.е. 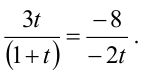
Пример:
Найти уравнение общей хорды двух окружностей: 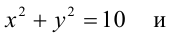
Решение:
Найдем точки пересечения окружностей, для этого решим систему уравнений: 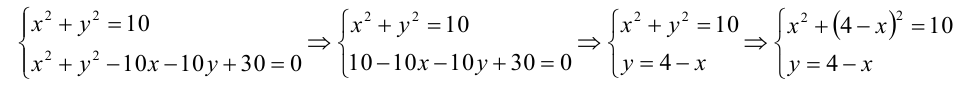
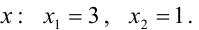
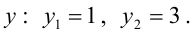
Пример:
Как расположены на плоскости точки, координаты которых удовлетворяют условиям
Решение:
Первое неравенство системы определяет внутренность круга, не включая границу, т.е. окружность с центром в точке (3,3) и радиуса 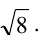
Пример:
Вычислить длину стороны квадрата, вписанного в эллипс, уравнение которого
Решение:
Пусть 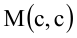
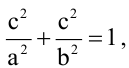
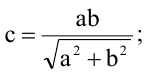
Пример:
Зная уравнение асимптот гиперболы 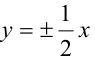
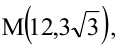
Решение:
Запишем каноническое уравнение гиперболы: 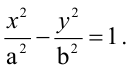
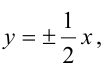
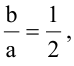
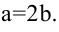
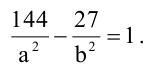
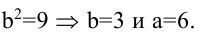
Пример:
Вычислить длину стороны правильного треугольника АВС, вписанного в параболу с параметром р, предполагая, что точка А совпадает с вершиной параболы.
Решение:
Каноническое уравнение параболы с параметром р имеет вид 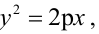
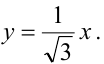
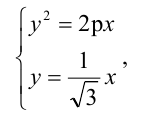
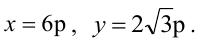
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Плоскость и прямая в пространстве
- Определитель матрицы
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Производные тригонометрических функции
- Производная сложной функции
- Пределы в математике
- Функции многих переменных
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Геометрические свойства линий второго порядка
Окружность
определяет окружность радиуса R с центром C(a; B).
Если центр окружности совпадает с началом координат, то есть если a=0, B=0, то уравнение (1) принимает вид
ЗАДАЧА 3704 Точка С(3; -1) является центром
Эллипс
Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами. Постоянную сумму расстояний произвольной точки эллипса до фокусов принято обозначать через 2а. Фокусы эллипса обозначают буквами F1 и F2 , расстояние между ними — через 2с. По определению эллипса 2a>2c или a>c.
Пусть дан эллипс. Если оси декартовой прямоугольной системы координат выбраны так, что фокусы данного эллипса располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение данного эллипса имеет вид
где b=sqrt(a^2-c^2); очевидно, a>b. Уравнение вида (1) называется каноническим уравнением эллипса.
При указанном выборе системы координат оси координат являются осями симметрии эллипса, а начало координат — его центром симметрии (рис.). Оси симметрии эллипса называются просто его осями, центр симметрии — просто центром. Точки, в которых эллипс пересекает свои оси, называются его вершинами. На рис. Вершины эллипса ABCD точки A’, A, B’, B. Часто осями эллипса называются также отрезки A’A=2a и B’B=2b; вместе с тем отрезок ОА=а называют большой полуосью эллипса, отрезок OB=b — малой полуосью.
Если фокусы эллипса расположены на оси Оу (симметрично относительно начала координат), то уравнение эллипса имеет тот же вид (1), но в этом случае b>a; следовательно, если мы желаем буквой а обозначать большую полуось, то в уравнении (1) нужно буквы а и b поменять местами. Однако для удобства формулировок задач мы условимся буквой а всегда обозначать полуось, расположенную на оси Ох, буквой b — полуось, расположенную на оси Оу, независимо от того, что больше, a или b. Если a=b, то уравнение (1) определяет окружность, рассматриваемую как частный случай эллипса.
где а — большая полуось, называется эксцентриситетом эллипса. Очевидно, ε F1M=r1 и F2M=r2 (рис.) называются фокальными радиусами точки М. Фокальные радиусы могут быть вычислены по формулам
Если эллипс определен уравнением (1) и a>b, то прямые
называются директрисами эллипса (если b>a, то директрисы определяются уравнениями y=-b/ε, y=b/ε)
Каждая директриса обладает следующим свойством: если r — расстояние от произвольной точки эллипса до некоторого фокуса, d — расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r/d есть постоянная величина, равная эксцентриситету эллипса:
ЗАДАЧА 3705 Эксцентриситет эллипса e=2/3, фокальный
ЗАДАЧА 3706 Эксцентриситет эллипса e=2/5, расстояние
Гипербола
где b=sqrt(c^2 — a^2) . Уравнение вида (1) называется каноническим уравнением гиперболы. При указанном выборе системы координат оси координат являются осями симметрии гиперболы, а начало координат — ее центром симметрии (рис.). Оси симметрии гиперболы называются просто ее осями, центр симметрии — центром гиперболы. Гипербола пересекает одну из своих осей; точки пересечения называются вершинами гиперболы. На рис. Вершины гиперболы ABCD точки А’ и А.
Прямоугольник со сторонами 2а и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником гиперболы.
Отрезки длиной 2a и 2b, соединяющие середины сторон основного прямоугольника гиперболы, также называют ее осями. Диагонали основного прямоугольника (неограниченно продолженного) являются асимптотами гиперболы, их уравнения суть
определяет гиперболу, симметричную относительно координатных осей, с фокусами на оси ординат; уравнение (2), как и уравнение (1), называется каноническим уравнением гиперболы; в этом случае постоянная разность расстояний от произвольной точки гиперболы до фокусов равна 2b.
Две гиперболы, которые определяются уравнениями
в одной и той же системе координат, называются сопряженными.
Гипербола с равными полуосями (a=b) называется равносторонней; ее каноническое уравнение имеет вид
где а — расстояние от центра гиперболы до ее вершины, называется эксцентриситетом гиперболы. Очевидно, для любой гиперболы ε > 1. Если М(x; y) — произвольная точка гиперболы, то отрезки F1M и F2M (см. рис.) называются фокальными радиусами точки М. Фокальные радиусы точек правой ветви гиперболы вычисляются по формулам
фокальные радиусы точек левой ветви — по формулам
Если гипербола задана уравнением (1), то прямые, определяемые уравнениями
называются ее директрисами (см. рис.). Если гипербола задана уравнением (2), то директрисы определяются уравнениями
Каждая директриса обладает следующим свойством: если r — расстояние от произвольной точки гиперболы до некоторого фокуса, d — расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r/d есть постоянная величина, равная эксцентрисистету гиперболы:
ЗАДАЧА 3707 Эксцентриситет гиперболы e=2, фокальный
ЗАДАЧА 3708 Эксцентриситет гиперболы e=3/2, центр ее
Парабола
Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F, расстояние от фокуса до директрисы — буквой р. Число р называется параметром параболы.
Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение
Фокальный радиус произвольной точки М(x; y) параболы (то есть длина отрезка F(M) может быть вычислен по формуле
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параболы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.
Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение
если она лежит в верхней полуплоскости (рис.), и
если в нижней полуплоскости (рис.)
Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.
ЗАДАЧА 3709 Вычислить фокальный радиус точки М
ЗАДАЧА 3710 Составить уравнение параболы, если даны
Полярное уравнение эллипса, гиперболы, параболы
Полярное уравнение, общее по форме для эллипса, одной ветви гиперболы и параболы, имеет вид
где p, θ — полярные координаты произвольной точки линии, р — фокальный параметр (половина фокальной хорды линии, перпендикулярной к ее оси), ε — эксцентриситет (в случае параболы ε = 1). Полярная система координат при этом выбрана так, что полюс находится в фокусе, а полярная ось направлена по оси линии в сторону, противоположную ближайшей к этому фокусу директрисы.
ЗАДАЧА 3711 Дано уравнение эллипса x^2/a^2 + y^2/b^2
ЗАДАЧА 3712 Дано уравнение гиперболы x^2/a^2 —
ЗАДАЧА 3713 Дано уравнение параболы y^2 = 2px.
Задачи для самостоятельного решения. 1 Составить уравнение хорды окружности х2+у2 = 49, делящейся в точке А(1;2) пополам
1 Составить уравнение хорды окружности х 2 +у 2 = 49, делящейся в точке А(1;2) пополам.
Ответ.х + 2у -5 = 0.
2. Определить координаты центров и радиусы окружностей:
Ответ: а) а = 4, b=-3, r= 5; б) а = -5, b = 2, r=0. Уравнение определяет точку;
в) а =2, b=-7, r 2 =-1. Уравнение не имеет геометрического смысла (мнимая, окружность).
3. Найти угол между радиусами окружности
х 2 +у 2 +4х-6у=0, проведенными в точки пересечения ее с осью Оу.
Ответ: tgφ=-2,4.
4. Составить уравнение окружности, проходящей через точки А(1; 2), В(0;-1), С(-3; 0).
Ответ: (х+1) 2 +(у -1) 2 =5.
5. Составить уравнение окружности, проходящей через точки А (7; 7) и В(-2; 4), зная, что ее центр лежит на прямой
Ответ: (х— З) 2 +(у-4) 2 =25.
6. Составить уравнение общей хорды окружностей х 2 +у 2 =16 и (х -5) 2 + у 2 = 9.
Ответ: х=3,2.
7. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса 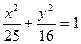
Ответ: 4х+3у+12= 0.
8. На прямой х+5=0 найти точку, одинаково удаленную от левого фокуса и верхней вершины эллипса 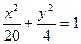
Ответ: М(—5; 7).
9. Пользуясь определением эллипса, составить его уравнение, зная, что точки F1 (0; 0) и F2 (1; 1) являются фокусами эллипса, а длина большой оси равна 2.
Ответ: Зх 2 + Зу 2 — 2ху — 2х — 2у — 1 == 0.
10. Составить уравнение геометрического места точек, расстояния которых от точки А (0; 1) з два раза меньше расстояния до прямой у—4=0.
Ответ: 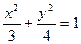
Занятие 16. Кривые второго порядка: гипербола, парабола
Гипербола.
Гиперболой называется геометрическое место точек, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (её обозначают через 2а), причем эта постоянная меньше расстояния между фокусами. Поместив фокусы гиперболы в точках F1(с; 0) и F2(-с;0), получаем уравнение гиперболы в виде 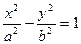

это простейшее (каноническое) уравнение гиперболы. Гипербола состоит из двух ветвей и расположена симметрично относительно осей координат. Точки А1(а;0) и А2(-а;0) называются вершинами гиперболы.
Отрезок А1А2=2а называют вещественной осью гиперболы, а отрезок В1В2=2b – мнимой осью (рис. 15).
Прямая называется асимптотой гиперболы, если расстояние точки гиперболы М (х;у) от этой прямой стремится к нулю при х→+∞ или х→-∞. Гипербола имеет две асимптоты, уравнения которых 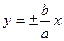
х = — а, у=b, у=-b. Прямые, проходящие через противоположные вершины этого прямоугольника, являются асимптотами гиперболы. На чертеже указано взаимное расположение гиперболы и ее асимптот. Отношение ε 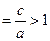
Если а=b, то уравнение гиперболы принимает вид
Такая гипербола называется равнобочной.

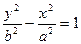
также является уравнением гиперболы, но вещественной осью этой гиперболы служит отрезок оси Оу длины 2b.
Две гиперболы 
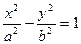
Пример 16.1.Эксцентриситет гиперболы равен 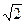
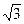
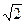
Решение. По определению эксцентриситета можем написать равенство 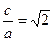
Другое равенство имеем из условия нахождения точки М на гиперболе, т. е. 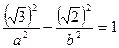
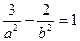
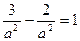
Таким образом, уравнение искомой гиперболы имеет вид х 2 — у 2 =1.
Парабола.
Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Если директрисой параболы 
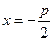
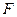
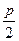


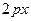
Эта парабола расположена симметрично относительно оси абсцисс (рис.6, где р 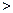
Уравнение

является уравнение параболы, симметричной относительно оси ординат. При p>0 параболы (16.1) и (16.2) обращены в положительную сторону соответствующей оси, а при p
Решение. Поскольку известны длина хорды и расстояние ее от вершины, то, следовательно , известны координаты конца этой хорды-точки М, лежащей на параболе. Уравнение параболы имеет вид 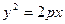

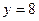
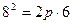

Таким образом, уравнение искомой параболы 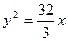
Пример 16.3. Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и отсекающей на биссектрисе 

Решение. Искомое уравнение параболы 

Длина хорды определяется как расстояние между двумя точками 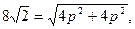
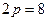

http://reshimvse.com/article.php?id=50
http://b4.cooksy.ru/articles/sostavit-uravnenie-obschey-hordy-paraboly-i-okruzhnosti