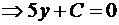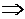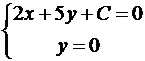Составить уравнение параболы касающейся прямой

Составить уравнение параболы касающейся прямой

Глава 20. Парабола

Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F , расстояние от фокуса до директрисы — буквой р. Число р называется параметром параболы.

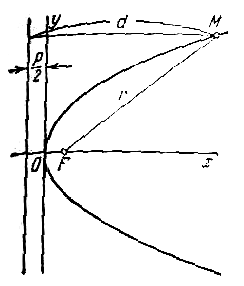
Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением

(1)

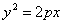
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение

.

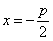
Фокальный радиус произвольной точки М( x; y ) параболы (то есть длина отрезка F(M ) может быть вычислен по формуле

.

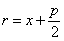
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.

Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид

(2)

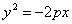
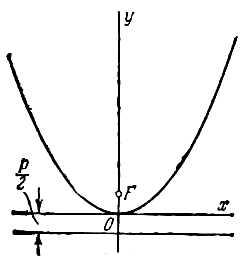
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение

(3)

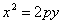
если она лежит в верхней полуплоскости (рис.), и

(4)

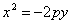
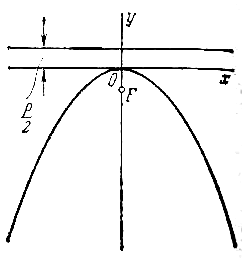
если в нижней полуплоскости (рис.)

Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.

Составить уравнение прямой которая касается параболы у2 8х и параллельна прямой 2х 2у 3 0

Составить уравнение прямой которая касается параболы у2 8х и параллельна прямой 2х 2у 3 0

Глава 20. Парабола

Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F , расстояние от фокуса до директрисы — буквой р. Число р называется параметром параболы.

Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением

(1)

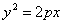
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение

.

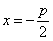
Фокальный радиус произвольной точки М( x; y ) параболы (то есть длина отрезка F(M ) может быть вычислен по формуле

.

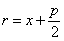
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.

Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид

(2)

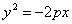
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение

(3)

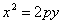
если она лежит в верхней полуплоскости (рис.), и

(4)

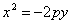
если в нижней полуплоскости (рис.)

Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.

Сборник задач по линейной алгебре и аналитической геометрии Учебное пособие (стр. 8 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9

15.25. Составить уравнение эллипса, если известны его эксцентриситет , фокус F(3,0) и уравнение соответствующей директрисы х+у-1=0.

15.26. Найти точки пересечения прямой х+2у-7=0 и эллипса х2+4у2=25.

15.27. Найти точки пересечения прямой 3х+10у-25=0 и эллипса .

15.28. Найти точки пересечения прямой 3х-4у-40=0 и эллипса .

15.29. Определить, при каких значениях m прямая у = — х + m 1)пересекает эллипс , 2)касается его, 3)проходит вне этого эллипса.

15.30. Составить уравнение касательной к эллипсу параллельной прямой 3х+2у+7=0.

16.1. Составить уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, зная, кроме того, что ее полуоси =6, b=18 (буквой обозначаем полуось гиперболы, расположенную на оси абсцисс).

16.2. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс, если расстояние между фокусами 2с=10 и эксцентриситет .

16.3. Составить уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, если уравнения асимптот у = и расстояние между вершинами равно 48.

16.4. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, если расстояние между директрисами равно и эксцентриситет .

16.5. Составить уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, если расстояние между директрисами равно и уравнения асимптот у = .

16.6. Дана гипербола 16х2-9у2 = -144. Найти 1)полуоси и b, 2)фокусы, 3)эксцентриситет, 4)уравнения асимптот, 5) уравнения директрис.

16.7. Вычислить площадь треугольника, образованного асимптотами гиперболы и прямой 9х+2у-24=0.

16.8. Дана гипербола определить фокальные радиусы точки М1.

16.9. Эксцентриситет гиперболы , фокальный радиус ее точки М, проведенный из некоторого фокуса, равен 16. Вычислить расстояние от точки М до односторонней с этим фокусом директрисы.

16.10.Эксцентриситет гиперболы , расстояние от точки М гиперболы до директрисы равно 4. Вычислить расстояние от точки М до фокуса, одностороннего с этой директрисой.

16.11. Эксцентриситет гиперболы , центр ее лежит в начале координат, один из фокусов F(12,0). Вычислить расстояние от точки М, гиперболы с абсциссой, равной 13, до директрисы, соответствующей заданному фокусу.

16.12. Эксцентриситет гиперболы , центр ее лежит в начале координат, одна из директрис дана уравнением х = -8. Вычислить расстояние от точки М1 гиперболы с абсциссой, равной 10, до фокуса, соответствующего заданной директрисе.

16.13. Определить точки гиперболы , расстояние которых до правого фокуса равно 4,5.

16.14. Определить точки гиперболы , расстояние которых до левого фокуса равно 7.

16.15. Составить уравнение гиперболы, фокусы которой лежат на оси абсцисс симметрично относительно начала координат, если даны точки М1(6,-1) и М2() гиперболы.

16.16. Составить уравнение гиперболы, фокусы которой лежат на оси ординат симметрично относительно начала координат, если даны точка гиперболы и эксцентриситет .

16.17. Составить уравнение гиперболы, фокусы которой лежат на оси абсцисс, симметрично относительно начала координат, если даны точка М гиперболы и уравнения асимптот у = .

16.18. Составить уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, если даны точка М1 гиперболы и уравнения директрис х = .

16.19. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс, симметрично относительно начала координат, если даны уравнения асимптот у = уравнения директрис х = .

16.20. Фокусы гиперболы совпадают с фокусами эллипса . Составить уравнения гиперболы, если ее эксцентриситет .

16.21. Составить уравнения гиперболы, фокусы которой лежат в вершинах эллипса , а директрисы проходят через фокусы этого эллипса.

16.22. Найти центр, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис гиперболы 16х2-9у2-64х-54у-161=0.

16.23. Найти центр, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис гиперболы 9х2-16у2+90х+32у-367=0.

16.24. Составить уравнения гиперболы, зная, что расстояние между ее вершинами равно 24 и фокусы F1(-10,2) и F2(16,2).

16.25. Составить уравнение гиперболы, зная, что фокусы F1(3,4) и F2(-3,-4) и расстояние между директрисами равно 3,6.

16.26. Составить уравнение гиперболы, если угол между асимптотами равен 90˚ и фокусы F1(4,-4) и F2(-2,2).

16.27. Составить уравнение гиперболы, если известны ее эксцентриситет , фокус F(5,0) и уравнение соответствующей директрисы 5х-16=0.

16.28. Найти точки пересечения прямой 2х-у-10=0 и гиперболы .

16.29. Найти точки пересечения прямой 4х-3у-16=0 и гиперболы .

17.1. Составить уравнение параболы, вершина которой находится в начале координат, зная, что парабола расположена симметрично относительно оси ОХ и проходит через точку А(9,6).

17.2. Составить уравнение параболы, вершина которой находится в начале координат, если парабола расположена симметрично оси ОХ и проходит через точку В(-1,3).

17.3. Составить уравнение параболы, вершина которой находится в начале координат, если парабола расположена симметрично относительно оси ОУ и проходит через точку С(1,1).

17.4. Составить уравнения параболы, вершина которой находится в начале координат, если парабола расположена симметрично относительно оси ОУ и проходит через точку D(4,-8).

17.5. Найти фокус F и уравнение директрисы параболы у2=24х.

17.6. Вычислить фокальный радиус точки М параболы у2=20х, если абсцисса точки М равна 7.

17.7. Вычислить фокальный радиус точки М параболы у2=12х, если ордината точки М равна 6.

17.8. На параболе у2=16х найти точки, фокальный радиус которых равен 13.

17.9. Составить уравнение параболы, если дан фокус F(-7,0) и уравнение директрисы х-7=0.

17.10. Найти вершину параболы и ее параметр у2=4-6х.

17.11. Найти вершину и параметр параболы х=-у2+2у-1.

17.12. Составить уравнение параболы, если даны ее фокус F(7,2) и директриса х-5=0.

17.13.Составить уравнение параболы, если ее фокус F(4,3) и директриса у+1=0.

17.14. Составить уравнение параболы, если даны ее фокус F(2,-1) и директриса х-у-1=0.

17.15. Даны вершина параболы А(6,-3) и уравнение ее директрисы

3х-5у+1=0. Найти фокус F этой параболы.

17.16. Даны вершина параболы (-2,-1) и уравнение ее директрисы х+2у-1=0. Составить уравнение этой параболы.

17.17. Определить точки пересечения прямой х+у-3=0 и параболы х2=4у.

17.18. Определить точки пересечения прямой 3х+4у-12=0 и параболы у2=-9х.

17.19. Определить точки пересечения прямой 3х-2у+6=0 и параболы у2=6х.

17.20. Определить при каких значениях углового коэффициента kпрямая

у = kх+2 а)пересекает параболу у2=4х, б)касается ее, в)проходит вне этой параболы.

17.21. Составить уравнение прямой, которая касается параболы у2=8х и параллельна прямой 2х+2у-3=0.

Уравнение параллельной прямой

Альтернативная формула:
Прямая, проходящая через точку M₁(x₁; y₁) и параллельная прямой Ax+By+C=0 , представляется уравнением

назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения параллельной прямой (см. также как составить уравнение перпендикулярной прямой).

Пример №2 . Написать уравнение прямой, параллельной прямой 2x + 5y = 0 и образующей вместе с осями координат треугольник, площадь которого равна 5.
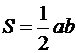
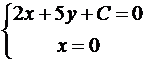
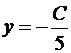
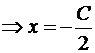
Решение. Так как прямые параллельны, то уравнение искомой прямой 2x + 5y + C = 0. Площадь прямоугольного треугольника , где a и b его катеты. Найдем точки пересечения искомой прямой с осями координат:
;
.
Итак, A(-C/2,0), B(0,-C/5). Подставим в формулу для площади: 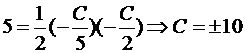. Получаем два решения: 2x + 5y + 10 = 0 и 2x + 5y – 10 = 0 .

Пример №3 . Составить уравнение прямой, проходящей через точку (-2; 5) и параллельной прямой 5x-7y-4=0 .
Решение. Данную прямую можно представить уравнением y = 5 /₇x – 4 /₇ (здесь a = 5 /₇). Уравнение искомой прямой есть y – 5 = 5 / 7(x – (-2)), т.е. 7(y-5)=5(x+2) или 5x-7y+45=0 .

Пример №4 . Решив пример 3 (A=5, B=-7) по формуле (2), найдем 5(x+2)-7(y-5)=0.

Пример №5 . Составить уравнение прямой, проходящей через точку (-2;5) и параллельной прямой 7x+10=0.
Решение. Здесь A=7, B=0. Формула (2) дает 7(x+2)=0, т.е. x+2=0. Формула (1) неприменима, так как данное уравнение нельзя разрешить относительно y (данная прямая параллельна оси ординат).