Составить уравнение параболы по вершине и директрисе

Составить уравнение параболы по вершине и директрисе

Глава 20. Парабола

Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F , расстояние от фокуса до директрисы — буквой р. Число р называется параметром параболы.

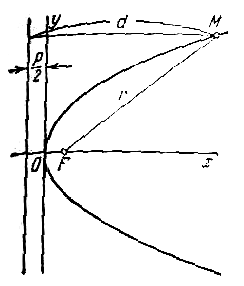
Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением

(1)

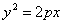
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение

.

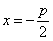
Фокальный радиус произвольной точки М( x; y ) параболы (то есть длина отрезка F(M ) может быть вычислен по формуле

.

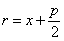
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.

Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид

(2)

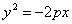
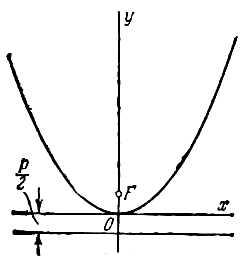
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение

(3)

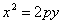
если она лежит в верхней полуплоскости (рис.), и

(4)

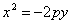
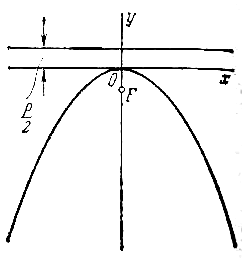
если в нижней полуплоскости (рис.)

Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.

Парабола

Парабола, её форма, фокус и директриса.

Параболой называется линия, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
y^<2>=2px\label
$$
при условии \(p > 0\).

Из уравнения \eqref вытекает, что для всех точек параболы \(x \geq 0\). Парабола проходит через начало канонической системы координат. Эта точка называется вершиной параболы.

Форма параболы известна из курса средней школы, где она встречается в качестве графика функции \(y=ax^<2>\). Отличие уравнений объясняется тем, что в канонической системе координат по сравнению с прежней оси координат поменялись местами, а коэффициенты связаны равенством \(2p=a^<-1>\).

Фокусом параболы называется точка \(F\) с координатами \((p/2, 0)\) в канонической системе координат.

Директрисой параболы называется прямая с уравнением \(x=-p/2\) в канонической системе координат (\(PQ\) на рис. 8.11).

Рис. 8.11. Парабола.

Свойства параболы.

Расстояние от точки \(M(x, y)\), лежащей на параболе, до фокуса равно
$$
r=x+\frac

<2>.\label
$$

Вычислим квадрат расстояния от точки \(M(x, y)\) до фокуса по координатам этих точек: \(r^<2>=(x-p/2)^<2>+y^<2>\) и подставим сюда \(y^<2>\) из канонического уравнения параболы. Мы получаем
$$
r^<2>=\left(x-\frac

<2>\right)^<2>+2px=\left(x+\frac

<2>\right)^<2>.\nonumber
$$
Отсюда в силу \(x \geq 0\) следует равенство \eqref.

Заметим, что расстояние от точки \(M\) до директрисы также равно
$$
d=x+\frac

<2>.\nonumber
$$

Следовательно, мы можем сделать следующий вывод.

Для того чтобы точка \(M\) лежала на параболе, необходимо и достаточно, чтобы она была одинаково удалена от фокуса и от директрисы этой параболы.

Докажем достаточность. Пусть точка \(M(x, y)\) одинаково удалена от фокуса и от директрисы параболы:
$$
\sqrt<\left(x-\frac

<2>\right)^<2>+y^<2>>=x+\frac

<2>.\nonumber
$$

Возводя это уравнение в квадрат и приводя в нем подобные члены, мы получаем из него уравнение параболы \eqref. Это заканчивает доказательство.

Параболе приписывается эксцентриситет \(\varepsilon=1\). В силу этого соглашения формула
$$
\frac=\varepsilon\nonumber
$$
верна и для эллипса, и для гиперболы, и для параболы.

Уравнение касательной к параболе.

Выведем уравнение касательной к параболе в точке \(M_<0>(x_<0>, y_<0>)\), лежащей на ней. Пусть \(y_ <0>\neq 0\). Через точку \(M_<0>\) проходит график функции \(y=f(x)\), целиком лежащий на параболе. (Это \(y=\sqrt<2px>\) или же \(y=-\sqrt<2px>\), смотря по знаку \(y_<0>\).) Для функции \(f(x)\) выполнено тождество \((f(x))^<2>=2px\), дифференцируя которое имеем \(2f(x)f'(x)=2p\). Подставляя \(x=x_<0>\) и \(f(x_<0>)=y_<0>\), находим \(f'(x_<0>)=p/y_<0>\) Теперь мы можем написать уравнение касательной к параболе
$$
y-y_<0>=\frac

>(x-x_<0>).\nonumber
$$
Упростим его. Для этого раскроем скобки и вспомним, что \(y_<0>^<2>=2px_<0>\). Теперь уравнение касательной принимает окончательный вид
$$
yy_<0>=p(x+x_<0>).\label
$$

Заметим, что для вершины параболы, которую мы исключили, положив \(y_ <0>\neq 0\), уравнение \eqref превращается в уравнение \(x=0\), то есть в уравнение касательной в вершине. Поэтому уравнение \eqref справедливо для любой точки на параболе.

Касательная к параболе в точке \(M_<0>\) есть биссектриса угла, смежного с углом между отрезком, который соединяет \(M_<0>\) с фокусом, и лучом., выходящим из этой точки в направлении оси параболы (рис. 8.12).

Рассмотрим касательную в точке \(M_<0>(x_<0>, y_<0>)\). Из уравнения \eqref получаем ее направляющий вектор \(\boldsymbol(y_<0>, p)\). Значит, \((\boldsymbol, \boldsymbol_<1>)=y_<0>\) и \(\cos \varphi_<1>=y_<0>/\boldsymbol\). Вектор \(\overrightarrow>\) имеет компоненты \(x_<0>=p/2\) и \(y_<0>\), а потому
$$
(\overrightarrow>, \boldsymbol)=x_<0>y_<0>-\frac

<2>y_<0>+py_<0>=y_<0>(x_<0>+\frac

<2>).\nonumber
$$
Но \(|\overrightarrow>|=x_<0>+p/2\). Следовательно, \(\cos \varphi_<2>=y_<0>/|\boldsymbol|\). Утверждение доказано.

Заметим, что \(|FN|=|FM_<0>|\) (см. рис. 8.12).

Задача 27702 Дана вершина параболы A (-2;-1) и.

Условие

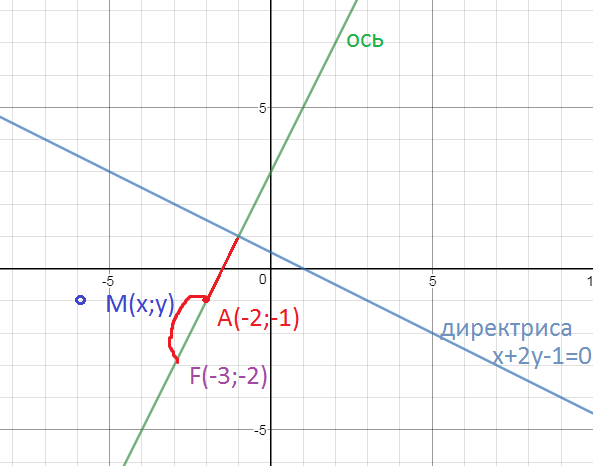
Дана вершина параболы A (-2;-1) и уравнение её директрисы x+2y-1=0.составить уравнение этой параболы.

Все решения

Составим уравнение оси, которая перпендикулярна директрисе и проходит через точку А.

Перпендикулярные ей прямые имеют вид
у=2х+b
Подставим координаты точки А и получим
b=3

Начало системы отсчета точка пересечения директрисы и перпендикулярной ей оси.
По рисунку видно ( можно и систему решить) точка (1;1)
Расстояние от вершины до директрисы равно расстоянию
от вершины до фокуса.
F(-3;-2)
Далее как в решении номера 3710

Пусть М(х;у)– любая точка параболы.
d_(1)=FM=sqrt((x+3)^2+(y+2)^2)
d_(2)=|x+2y-1|/sqrt(1+2^2)-см. формулу расстояния от точки до прямой
d_(1)=d_(2)
sqrt((x+3)^2+(y+2)^2)=|x+2y-1|/sqrt(5)
Возводим в квадрат и преобразовываем
(x–4)^2+(y-3)^2=(x+2y-1)^2/5
x^2-8x+16+y^2-6y+9=(x^2+4y^2+1-2x-4y+4xy)/5;
5x^2-40x+80+5y^2-30y+45-x^2-4y^2-1+2x+4y-4xy=0
4x^2-4xy+y^2-38x-26y+124=0
О т в е т.
4x^2-4xy+y^2-38x-26y+124=0