Составить уравнение параболы с вершиной в начале координат

Составить уравнение параболы с вершиной в начале координат

Глава 20. Парабола

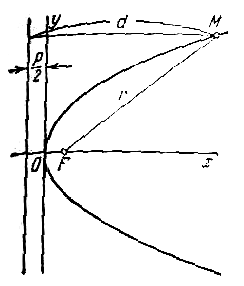
Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F , расстояние от фокуса до директрисы — буквой р. Число р называется параметром параболы.

Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением

(1)

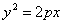
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение

.

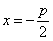
Фокальный радиус произвольной точки М( x; y ) параболы (то есть длина отрезка F(M ) может быть вычислен по формуле

.

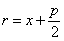
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.

Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид

(2)

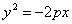
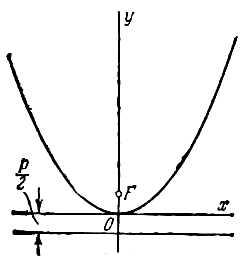
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение

(3)

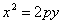
если она лежит в верхней полуплоскости (рис.), и

(4)

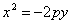
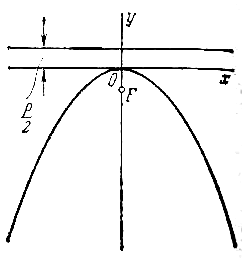
если в нижней полуплоскости (рис.)

Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.

Квадратичная функция. Построение параболы

О чем эта статья:

8 класс, 9 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные понятия

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ: наглядно.

• Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.

Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.

Построение квадратичной функции

Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:

График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :

Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x 2 , нужно составить таблицу:

x

y

Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.

График функции y = –x 2 выглядит, как перевернутая парабола:

Зафиксируем координаты базовых точек в таблице:

x

y

Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:

• Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
• Если старший коэффициент меньше нуля a 2 + bx + c, для построения которой нужно решить квадратное уравнение ax 2 + bx + c = 0. В процессе найдем дискриминант D = b 2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.

Рассмотрим три случая:

1. Если D 0,то график выглядит так:

1. Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
2. Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:

Если a > 0, то график выглядит как-то так:

0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>

На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.

Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).

На изображении отмечены основные параметры графика квадратичной функции:

Алгоритм построения параболы

Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.

Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.

Разберем общий алгоритм на примере y = 2x 2 + 3x — 5.

Как строим:

1. Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена 2x 2 + 3x — 5.

D = b 2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0

В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:

2x 2 + 3x — 5 = 0 2 + 3x — 5 = 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAPoAAAAyCAYAAAB1V8bkAAAJyElEQVR4Ae2c16sUwRLGfdRX/wXFB30QFFQUQUyIKCIGBEEQzCCoKIgB01ExZwVz4JpzztljwJxzzjlnrcuvL33unD2zOzO7OzvuThU0u5N6uuvrr7u6unrKiYpqQDVQ8BooV/A11AqqBlQDokTXRqAaiIEGlOgxAFmrqBpQomsbUA3EQANK9BiArFVUDSjRtQ2oBmKgASV6DEDWKqoGlOjaBlQDMdBAQRH9z58/8vv3b5P+/v2bMXy/fv0S8kxMGWesGRgNpIMXz7jhkg28CxmWgiH69+/f5dSpU7JixQpZtmyZXLx4UX7+/JkUOxoGjSaVTJw4UVatWiUbNmwoSYcPH071iF7zqYGgeNlsT58+LZMnTy7BA2y2bNkib9++tbfor4sGCobogD19+nR5/fq1nDx5Upo0aSLHjh2TZD39x48f5ebNmy4q+d8pRo327dtLo0aNTF6NGzeWevXqCeRXyVwDQfHijXTMmzZtMjiAL6lu3brSuXNnuXfvXuaFKuAcCobojOQDBgwwgD948EAg5ubNm42Z54bfjRs3ZMqUKW6XzDk6jP379wsjD/LmzRtZt26dvHr1KukzesG/BoLiRc5gceXKFZM4/vbtmxw6dEguXbokP3788P/yGN5ZMET/8uWLvHv3Tt6/f2/Muh49esj169eTQupF9MQHIfm1a9cST+txmhoIipfba86fPy9Hjx4VrDOV1BooGKJTTYh++fJlGTt2rCxevNgcJ6t+EKIz3587d26yrPR8mhoIglfiK549e2Y6dHBU8dZA3hH9+PHjYhNmnFO+fv1qTOwDBw5Ily5dhF+nQ47ndu/ebdLChQule/fuJcecp9E477d5d+zYUW7fvm0P9TeABixW/AbBCz+LffbChQtl3rh69WpZsmSJjuZlNON+Iu+IDkGZW+N427Ztm6nVp0+f5MiRI6Zh2Dl1hw4dZOjQoaVGdebc1oM+a9Ys48Sxx/y6zfUePnwoVapUcdeenvXUQLp4LV261OA8bdo0g5nzRR8+fJBhw4YJeav400DeEf3Ro0dmZGD+/fLlS1NLzLjhw4fLmDFjhEaA4DHv16+fGeHdVOHXdKczqVy5slsWes6HBtLF6/HjxwZn/CLPnz8v9aZbt25Jt27dlOiltJL6IO+I7lYdTPY1a9bIjBkz5M6dO7Jjxw5hRN++fXtSb6xfos+ZM0cqVark9trQzrEmXFxc7LnOH1oBQs44HbycRTpz5oy0a9funyA6DkGW/NavX19mauIsc+J/OkCmJliRL168ME7FVM7jxOeDHhcE0ak05KD3P3v2rFkWO3HihHz+/DmpPlh3XbRoUdLr9gL5LF++3B6G+nv//n3ZuHGjDBw4UDp16pS0kwq1EDnKPChezmI9efJEtm7dmnJVxXl/WP8PHjxopoxXr141RG3Tpo0JsPLzPqaaLVq0kDp16kjDhg2lb9++JgbEz7Pp3FMwRKfyBLkwX2fpxivqjbm8Nf1TKY77WK/NhVBuGvGoUaNMHID1N+Ti3VG8IwhezvIR5gwm/EYlrBgMGTJE9u3bZxy4YDV69Gjf/py9e/fKypUrjSVKLEDYqwcFRfSoQM/2e2fOnGmivgqd6NnWWy7zI3CqefPmUlRUVOIXgrzly5cXfEZewr2Y/XTuyaI3vfIIcj1tolM4lpyIBZ83b56MGzdO9uzZY0YjwkSfPn0apBx6r0MDYRBd8XIoOAt/sRiZU0N4az2OHz9eKlSo4MvSgOgs6RKIBYdIYUraRMfsYpkL84m5cc+ePY1DYv78+dKnTx/B2eAlmKldu3b1TISy5luII8s/XnWbNGmSMC9PlDCIrniJcXB6YcJ15s9+JHEkrlq1qixYsMDPowLRcRqzSgSHiOkI0xeUNtHpxXBUIQQ3tGrVKnLniC8N58FNYRBd8QoOPES2Php8Agw2dvR25gZRcaaNHDnSeTrlf/JxdhTsuMQacJ5LmUHAi2kT3b6HyrNBoXXr1uYUBXVThr3f+YuCcGp4JZRsFYAV8K8lt1hremqveuE4RAeJEgbR7Tvigpfb1JG6e2HCde5DCJbCM16rVi2T2D9BiLVT6Agwv3GsgSXPumHqfAZ+sLqCNWfbNQ455ve8MwxJm+gsXeF0YFcXPRlRaAiebD/OCO5l/XDQoEGeCTPHhqZWq1ZN/rVElF2iTJ061bNemHkEhiRKGESPG141atRIVKtZevXT3tjz7kcYgIioZDRmtyM6Zk09sf0zbYIndkBgabFt27ZmeZeYAgQzvmLFimWe9VMOP/ekTXTWMXv37m16uF69esmECRNMZdgDzgcgVIJrwLm8Vr9+fSECjM4wG6J4ZUOL/8+DgQdSwwGccIRkk4jITBRGaZZM8V/ZlRRGdIJlwJzBsX///gKPwpK0iY7HkArSgKgwu8XYMnju3LmkgSr0ZNZUCatCfvLFtKIHtj2sn2dycY8NmCGcF6cQIwXx+dmQfMMLfEj/qjA1Yx29ZcuWpRLmfaLcvXtXBg8eLCNGjChxUoM1mBAdt3btWmP9ZatTT3w/x2kTHcKytAB5EeYmyYiDecpWz9mzZyf9EIRb4cI6Rw/KikGcLI98w4vlWkKYC0Uw5xkEMeGt4A/Akc28P+wBMG2i28L6+WV7IruRmjVrVmK6+HkujHuYL+3atcuUhbm/SlkNRI0Xn/iqWbOmaTNlS5d/ZzDzITOhslFJTohO5Rg98WDaOUoUFabXpBExV2JThBI9OQpR4YX1x3SQb/UxOBSCYO2yA48RPCqJFdGZmxN8w/q/Ej11k4uK6ERXMqflw4+FQvTUms7N1VgRnYgndq2RlOipG1gURCf2myhLpldNmzZVoqeGKNDV2BAdj+bOnTuNcpTo3m0k10THrCVohCAiRInujVGQO2JDdJYA8bQTpIJHt3bt2mZtk1FEpawGck10PrRB4BEf4QQjgqIIK2UbqErmGsgJ0fE2AmL16tWFj/oRwpprYcRgVCcR+URsPkELBCyolNZAFHgRVcZyrcWoQYMGwtd97KfBSpdQj4JqICdEZ3kBkwwQIZZXLHDQSvi9H687G/wJgyREkl+7McdvHnG4L0q8WG9mUOCDnASf4DxVyVwDOSF65sXMXg6QnYbMMh+/fjfgZK8EmlMqDYAPzji7WyyqQSFVGfPxWuyIno8gaZlVA5lqQImeqQb1edVAHmhAiZ4HIGkRVQOZakCJnqkGI3m+WIrKlZOi45G8XF+ahxpQouchaKbIx4uU6PmKXQTlVqJHoPTMX/lM/tOuSIozz0hziIkGlOgxAVqrGW8NKNHjjb/WPiYaUKLHBGitZrw1oESPN/5a+5hoQIkeE6C1mvHWwH8BSUfSiO3XWNEAAAAASUVORK5CYII=»>

1. Координаты вершины параболы:

1. Точка пересечения с осью OY находится: (0; -5) и ей симметричная.
2. Нанести эти точки на координатную плоскость и построить график параболы:
   2 + 3x — 5 = 0″ height=»671″ src=»https://lh6.googleusercontent.com/TYyA5dFfh0ZKINaPSps3Y_X1mCv8Mhv_8bNG3_dPbZud1AEsvo7UBFmVQNm1GcR1CQFo6HE1lNjYaAgepQUTQiK_ay_Fnuv7LEsB53woHkFO66W0R1PP8QfGsFcYzaR_h4AJdLxC» width=»602″>

Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀

Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x 2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.

Рассмотрим пример: y = 2 * (x — 1) 2 + 4.

Как строим:

1. Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:

• построить y = x 2 ,
• умножить ординаты всех точек графика на 2,
• сдвинуть его вдоль оси ОХ на 1 единицу вправо,
• сдвинуть его вдоль оси OY на 4 единицы вверх.

1. Построить график параболы для каждого случая. 2 + y₀» height=»431″ src=»https://lh5.googleusercontent.com/_zgF-CXWf4Yy0p2OnBYSJkUm0zO-mNetq5feU6LIPEbIgSrO9kdr2ti_tr7Gg3yTMOlJVnuZgG0HleAFfAzG7yr7ELHT6KSMqMrRHkHqt-VcgIiSZx80cVj0zlPMBzEM0wAWQ-L6″ width=»602″>

Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)

Рассмотрим следующий пример: y = (x − 2) × (x + 1).

Как строим:

Данный вид уравнения позволяет быстро найти нули функции:

(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.

Определим координаты вершины параболы:

Найти точку пересечения с осью OY:

с = ab = (−2) × (1) = −2 и ей симметричная.

Отметим эти точки на координатной плоскости и соединим плавной прямой.

Высшая математика (стр. 27 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

или .

Пример 38. Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Ох и отсекающей от прямой хорду длиной .

Решение. Прямая проходит через начало координат , так как является биссектрисой I и II координатных углов. Искомая парабола симметрична относительно оси Ох, поэтому уравнение параболы может иметь вид или . Рассмотрим каждый из этих случаев. Если , то вторая точка пересечения прямой с параболой , , значит и , то есть точка . Длина хорды определяется как расстояние между двумя точками и : , , , тогда , а значит искомое уравнение параболы

.

Рассмотрим второй случай, когда уравнение параболы имеет вид . Найдем точки пересечения параболы и данной прямой.

, , , , . Получили две точки и .

Далее, рассуждая аналогично первому случаю, получаем: , , . Тогда искомое уравнение параболы .

Таким образом, условиям задачи удовлетворяют два уравнения параболы: и .

Можно сделать вывод, что общее уравнение кривой второго порядка (2.41) может быть уравнением параболы, если коффициенты , или , , то есть одна из переменных должна быть в первой степени.

Но не всякое уравнение вида (2.41) определяет кривую второго порядка. Например, не существует точек плоскости, удовлетворяющих уравнению .

Задачи для самостоятельного решения.

1. Дана точка . Составить уравнение окружности, диаметром которой служит отрезок ОА.

2. Составить уравнение окружностьи, проходящей через точки и , если ее центр лежит на прямой .

3. Эллипс, симметричный относительно осей координат, проходит через точки и . Составить уравнение эллипса и найти расстояния точки М от фокусов.

4. Эллипс, симметричный относительно осей координат, проходит через точки и . Составить уравнение эллипса и найти эксцентриситет. Построить эллипс.

5. Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих фокусах и вершинах эллпса .

6. Составить уравнение гиперболы, если ее эксцентриситет равен 2 и фокусы совпадают с фокусами эллипса . Построить гиперболу.

7. Составить уравнение параболы, симметричной относительно оси Ох, с вершиной в начале координат, если длина некоторой хорды этой параболы, перпендикулярной к оси Ох, равна 16, а расстояние этой хорды от вершины равно 6.

8. Парабола отсекает от прямой, проходящей через начало координат, хорду, равную . Составить уравнение этой прямой.

Ответы. 1. . 2. .

3. ; . 4. . 5. . 6. . 7. . 8. .

Контрольная работа по теме «Элементы аналитической геометрии и кривые II порядка».

Даны вершины треугольника , , . Найти 1) уравнение стороны АВ; 2)угол при вершине А; 3) уравнение и длину высоты CD; 4) точку пересечения медианы треугольника. Сделать чертеж.

1.1. , , .

1.2. , , .

1.3. , , .

1.4. , , .

1.5. , , .

1.6. , , .

1.7. , , .

1.8. , , .

2.1. Составить каноническое уравнение эллипса, у которого малая полуось равна 4, а расстояние между фокусами равно 10.

2.2. Определить координаты центра и радиус окружности .

2.3. Составит уравнение гиперболы, проходящейц через точки и .

2.4. На параболе найти точку, расстояние которой до директрисы параболы равно 4.

2.5.Составить каноническое уравнение эллипса, зная, что большая полуось равна 6, а эксентриситет .

2.6. Составить каноническое уравнение гиперболы, если расстояние между фокусами равно 10, а между вершинами 8.

2.7. Составить уравнение параболы, симметричной относительно оси Оу, проходящей через точку , вершина которой лежит в начале координат.

2.8. Определить координаты центра и радиус окружности .

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Красс для экономических специальностей. – М.: ИНФРА-М, 1998.

2. Солодовников в экономике. Ч.1,2. – М.: Финансы и статистика, 1999.

3. Беклемишев аналитической геометрии и линейной алгебры. – М.: Наука, 1984.

4. Ефимов курс аналитической геометрии. – М.: Наука, 1975.

5. Крамер математика для экономистов. – М.: ЮНИТИ, 1998.

6. , , Кожевникова математика в упражнениях и задачах. Ч.1. – М.: Высшая школа, 1980.

7. , Никольский линейной алгебры и аналитической геометрии. – М.: Наука, 1980.

8. Лопатников -математический словарь. – М.:Наука, 1993.

9. Шипачев высшей математики. – М.: Высшая школа, 1994.

10. Шипачев задач по высшей математике. – М.: Высшая школа, 1994.

1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ 4

1.1. Определители 4

1.1.1. Определители второго порядка 4

1.1.2. Опренделители третьего порядка 4

1.1.3. Свойства определителей 7

1.1.4. Определители четвертого порядка

Методы их вычисления. 11

1.2.1. Основные понятия 15

1.2.2. Действия над матрицами 18

1.2.3. Обратная матрица 23

1.2.4. Ранг матрицы 28

1.3. Системы линейных уравнений 33

1.3.1. Основные понятия 33

1.3.2. Теорема Кронекера – Копелли 34

1.3.3. Матричный метод решения систем 41

1.3.4. Решение систем линейных уравнений по формулам Крамера 43

1.3.5. Решение систем методом Гаусса 45

1.3.6. Однородные системы уравнений 49

Индивидуальное домашнее задание по теме «Элементы линейной алгебры» 55

2. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ 57

2.1. Векторы. Основные понятия 57

2.2. Линейные операции над векторами 58

2.3. Проекция вектора на ось 61

2.4. Координаты вектора 64

2.5. Деление отрезка в данном отношении 68

2.6. Скалярное произведение векторов и его свойства 70

2.7. Векторное произведените векторов и его свойства 74

2.8. Смешанное произведение векторов и его свойства 78

Контрольная работа по теме «Векторная алгебра» 81

2.9. Прямая на плоскости 83

2.10. Кривые второго порядка 94

Контрольная работа по теме «Элементы аналитической геометрии и кривые II порядка» 108