Составить уравнение параболы симметричной относительно оси ox

Составить уравнение параболы симметричной относительно оси ox

Глава 20. Парабола

Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F , расстояние от фокуса до директрисы — буквой р. Число р называется параметром параболы.

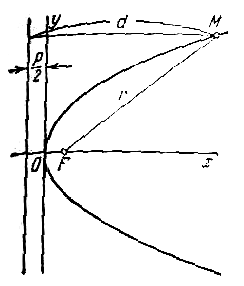
Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением

(1)

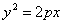
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение

.

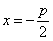
Фокальный радиус произвольной точки М( x; y ) параболы (то есть длина отрезка F(M ) может быть вычислен по формуле

.

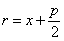
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.

Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид

(2)

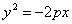
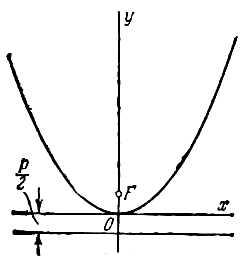
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение

(3)

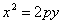
если она лежит в верхней полуплоскости (рис.), и

(4)

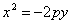
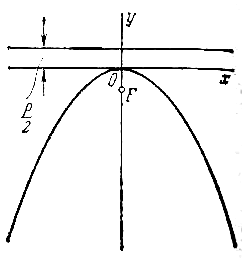
если в нижней полуплоскости (рис.)

Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.

Высшая математика (стр. 27 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

или .

Пример 38. Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Ох и отсекающей от прямой хорду длиной .

Решение. Прямая проходит через начало координат , так как является биссектрисой I и II координатных углов. Искомая парабола симметрична относительно оси Ох, поэтому уравнение параболы может иметь вид или . Рассмотрим каждый из этих случаев. Если , то вторая точка пересечения прямой с параболой , , значит и , то есть точка . Длина хорды определяется как расстояние между двумя точками и : , , , тогда , а значит искомое уравнение параболы

.

Рассмотрим второй случай, когда уравнение параболы имеет вид . Найдем точки пересечения параболы и данной прямой.

, , , , . Получили две точки и .

Далее, рассуждая аналогично первому случаю, получаем: , , . Тогда искомое уравнение параболы .

Таким образом, условиям задачи удовлетворяют два уравнения параболы: и .

Можно сделать вывод, что общее уравнение кривой второго порядка (2.41) может быть уравнением параболы, если коффициенты , или , , то есть одна из переменных должна быть в первой степени.

Но не всякое уравнение вида (2.41) определяет кривую второго порядка. Например, не существует точек плоскости, удовлетворяющих уравнению .

Задачи для самостоятельного решения.

1. Дана точка . Составить уравнение окружности, диаметром которой служит отрезок ОА.

2. Составить уравнение окружностьи, проходящей через точки и , если ее центр лежит на прямой .

3. Эллипс, симметричный относительно осей координат, проходит через точки и . Составить уравнение эллипса и найти расстояния точки М от фокусов.

4. Эллипс, симметричный относительно осей координат, проходит через точки и . Составить уравнение эллипса и найти эксцентриситет. Построить эллипс.

5. Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих фокусах и вершинах эллпса .

6. Составить уравнение гиперболы, если ее эксцентриситет равен 2 и фокусы совпадают с фокусами эллипса . Построить гиперболу.

7. Составить уравнение параболы, симметричной относительно оси Ох, с вершиной в начале координат, если длина некоторой хорды этой параболы, перпендикулярной к оси Ох, равна 16, а расстояние этой хорды от вершины равно 6.

8. Парабола отсекает от прямой, проходящей через начало координат, хорду, равную . Составить уравнение этой прямой.

Ответы. 1. . 2. .

3. ; . 4. . 5. . 6. . 7. . 8. .

Контрольная работа по теме «Элементы аналитической геометрии и кривые II порядка».

Даны вершины треугольника , , . Найти 1) уравнение стороны АВ; 2)угол при вершине А; 3) уравнение и длину высоты CD; 4) точку пересечения медианы треугольника. Сделать чертеж.

1.1. , , .

1.2. , , .

1.3. , , .

1.4. , , .

1.5. , , .

1.6. , , .

1.7. , , .

1.8. , , .

2.1. Составить каноническое уравнение эллипса, у которого малая полуось равна 4, а расстояние между фокусами равно 10.

2.2. Определить координаты центра и радиус окружности .

2.3. Составит уравнение гиперболы, проходящейц через точки и .

2.4. На параболе найти точку, расстояние которой до директрисы параболы равно 4.

2.5.Составить каноническое уравнение эллипса, зная, что большая полуось равна 6, а эксентриситет .

2.6. Составить каноническое уравнение гиперболы, если расстояние между фокусами равно 10, а между вершинами 8.

2.7. Составить уравнение параболы, симметричной относительно оси Оу, проходящей через точку , вершина которой лежит в начале координат.

2.8. Определить координаты центра и радиус окружности .

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Красс для экономических специальностей. – М.: ИНФРА-М, 1998.

2. Солодовников в экономике. Ч.1,2. – М.: Финансы и статистика, 1999.

3. Беклемишев аналитической геометрии и линейной алгебры. – М.: Наука, 1984.

4. Ефимов курс аналитической геометрии. – М.: Наука, 1975.

5. Крамер математика для экономистов. – М.: ЮНИТИ, 1998.

6. , , Кожевникова математика в упражнениях и задачах. Ч.1. – М.: Высшая школа, 1980.

7. , Никольский линейной алгебры и аналитической геометрии. – М.: Наука, 1980.

8. Лопатников -математический словарь. – М.:Наука, 1993.

9. Шипачев высшей математики. – М.: Высшая школа, 1994.

10. Шипачев задач по высшей математике. – М.: Высшая школа, 1994.

1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ 4

1.1. Определители 4

1.1.1. Определители второго порядка 4

1.1.2. Опренделители третьего порядка 4

1.1.3. Свойства определителей 7

1.1.4. Определители четвертого порядка

Методы их вычисления. 11

1.2.1. Основные понятия 15

1.2.2. Действия над матрицами 18

1.2.3. Обратная матрица 23

1.2.4. Ранг матрицы 28

1.3. Системы линейных уравнений 33

1.3.1. Основные понятия 33

1.3.2. Теорема Кронекера – Копелли 34

1.3.3. Матричный метод решения систем 41

1.3.4. Решение систем линейных уравнений по формулам Крамера 43

1.3.5. Решение систем методом Гаусса 45

1.3.6. Однородные системы уравнений 49

Индивидуальное домашнее задание по теме «Элементы линейной алгебры» 55

2. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ 57

2.1. Векторы. Основные понятия 57

2.2. Линейные операции над векторами 58

2.3. Проекция вектора на ось 61

2.4. Координаты вектора 64

2.5. Деление отрезка в данном отношении 68

2.6. Скалярное произведение векторов и его свойства 70

2.7. Векторное произведените векторов и его свойства 74

2.8. Смешанное произведение векторов и его свойства 78

Контрольная работа по теме «Векторная алгебра» 81

2.9. Прямая на плоскости 83

2.10. Кривые второго порядка 94

Контрольная работа по теме «Элементы аналитической геометрии и кривые II порядка» 108

2.5 Парабола

Парабола Есть геометрическое место точек на плоскости, равноотстоящих от данной точки, называемой фокусом, и данной прямой, называемой директрисой.

Выберем систему координат таким образом (рисунок 2.7): за ось ОХ примем прямую, проходящую через фокус F перпендикулярно к директрисе, за положительное направление примем направление от директрисы к фокусу. За начало координат примем середину О отрезка от точки F до директрисы, длину которого обозначим через Р и будем называть параметром параболы. Пусть М(Х, У) произвольная точка, лежащая на параболе. Пусть точка N основание перпендикуляра, опущенного из М На директрису. По определению параболы MN = MF.

Из этого условия получаем Каноническое уравнение параболы в выбранной системе координат

Пусть P > 0, исследуем форму параболы.

Из канонического уравнения параболы видно, что Х не может принимать отрицательных значений, т. е. все точки параболы лежат справа от оси ОY. Уравнение содержит переменную У В квадрате, значит парабола симметрична относительно оси ОХ, эта ось называется Осью Параболы. Точка О пересечения параболы с ее осью симметрии называется Вершиной параболы.
Для параболы, заданной уравнением (2.11), вершина совпадает с началом координат, а ось симметрии – с осью ОХ. График параболы имеет вид, изображенный на рисунке 2.7. Уравнение директрисы записывается в виде .

Фокус параболы для параболы с осью симметрии – осью Х имеет вид F(,0), а для параболы с осью симметрии осью Y – F(0,).

Определяет параболу, область определения которой .

Имеет вершину в начале координат, фокус , директрису ; ветви параболы направлены в положительную сторону оси OY и ветви направлены в отрицательную сторону оси OY, если уравнение параболы Х2 = –2Py. Осью симметрии такой параболы является ось ОY, а вершиной – начало координат.

Пример 2.4. Составить уравнение параболы и ее директрисы, зная, что она симметрична относительно оси ОY, фокус находится в точке F(0; 2), вершина совпадает с началом координат.

Решение. Будем искать уравнение параболы в виде Х2 = 2Py, так как по условию она симметрична относительно оси OY.

По условию , а значит, P = 4. Итак, искомое уравнение имеет вид Х2 = 8У, уравнение ее директрисы у = –2.