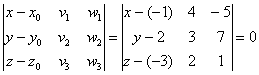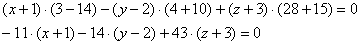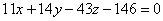Составить уравнение плоскости по 2 направляющим векторами

Пункт 2. Вывод уравнения плоскости по точке и двум направляющим.

Пусть даны точка и 2 направляющих вектора ими однозначно порождается некоторый параллелограмм, а следовательно и плоскость. Одного направляющего вектора недостаточно, ведь тогда плоскость может вращаться вокруг него, то есть плоскость не будет однозначно фиксирована.

Обозначим координаты направляющих, например, так: и .

Первый способ. Можно найти нормаль к плоскости как векторное произведение 2 направляющих векторов и далее искать уравнение плоскости по точке и нормали, методом, рассмотренным в пункте 1. Но это будет решение в 2 шага.

Однако можно также получить уравнение плоскости сразу, без вычисления векторного произведения:

Второй способ.Возьмём произвольную точку . Если она принадлежит плоскости, то вектор (показан красным цветом) будет лежать в плоскости, то есть тройка векторов , образует линейно-зависимую систему (ЛЗС), то есть эти векторы не образуют параллелепипед, а лежат в одной плоскости.

Тогда смешанное произведение 0, то есть определитель, составленный из них, равен 0:

Вычисляя этот определитель, мы получим в качестве результата некоторое уравнение, содержащее x,y,z. А если начальная точка (0,0,0), то уравнение будет вычисляться с помощью такого определителя: .

Пример.Построить уравнение плоскости, проходящей через начало координат, параллельно 2 направляющим (1,2,3) и (1,1,1).

Решение. . Можем разложить по первой строке: = .

Для удобства, чтобы 1-й коэффициент был положителен, можно домножить на . Ответ: .

Замечание.Векторы можно поменять местами, и это не влияет на уравнение плоскости. Неважно, какой из них считается первым, а какой вторым. Если все миноры сменят знак, то из уравнения просто можно будет вынести коэффициент .

Замечание. Построение уравнения плоскости по трём точкам. Если дано 3 точки, достаточно взять 2 направляющих и (пусть это и будут те самые ) и затем действовать так, как сказано ранее.

Лекция № 7. 14. 10. 2016

Пункт 3. Расстояние от точки до плоскости.

Пусть дано уравнение плоскости и произвольная точка .

Возможно, она лежит в плоскости (тогда расстояние по формуле автоматически получится 0). Но в общем случае она не принадлежит плоскости. Мы не знаем, где основание перпендикуляра, более того, его и не потребуется искать.

Возьмём произвольную точку в плоскости. Сделать это просто: присвоим какие-нибудь значения 2 переменным из трёх, и вычислим третью. Например, как правило, задать x,y и вычислить z.

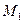
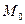
Итак, выбрали какую-то точку в плоскости. Отрезок между и не перпендикулярен плоскости, но его проекция на нормаль — это как раз и есть кратчайшее расстояние до плоскости (d).

= =

.

Если подставить в уравнение плоскости (в числителе) точку, лежащую в плоскости, то получим 0. В общем же случае, результат подстановки некоторой точки, не лежащей в плоскости, в уравнение плоскости, характеризует удаление от плоскости.

Пункт 4. Взаимное расположение плоскостей

Пусть даны 2 плоскости.

Если рассматривать это как систему уравнений, то видим, что 2 уравнения и 3 переменных, то есть по меньшей мере одна свободная переменная. Это означает, что если решения есть, то их бесконечно много. Это и есть все точки, принадлежащие прямой, являющейся пересечением плоскостей.

Чтобы найти пересечение, достаточно решить систему уравнений, где 2 уравнения — это и есть уравнения этих плоскостей.

Если то плоскости совпадают, так как уравнения полностью пропорциональны.

Если то плоскости параллельны. Дело в том, что если из одного уравнения вычесть кратное второму, то получим все 0 коэффициенты при x, y, z, и останется противоречивое уравнение (некая ненулевая константа = 0).

Если пропорциональность нарушена среди каких-то из первых 3 дробей, то плоскости пересекаются по прямой.

Пункт 5. Угол между плоскостями и метод его нахождения.

Можно искать как угол между нормалями (показаны красным). Их координаты известны — это и . В то же время известно, что . Тогда = . .

Прямая в пространстве.

Для прямой на плоскости и для плоскости в пространстве есть однозначно определённое направление нормали (перпендикуляра) т.к. там размерности рассматриваемых многообразий 1 и 2 (2 и 3 соответственно), то есть «не хватает» одной размерности. А для прямой в пространстве не хватает 2 размерностей (1 и 3). Это совершенно новый случай, здесь нельзя однозначно задать перпендикуляр. Есть целая плоскость, перпендикулярная прямой, то есть бесконечное число нормалей. А вот направляющий вектор однозначно определён (с точность до его длины, конечно). Это проявится в том, что мы получим другой тип уравнений.

5.2.1. Как составить уравнение плоскости
по точке и двум неколлинеарным векторам?

Конструировать уравнение будем с помощью векторов и точек. Их должно быть как можно меньше, но достаточно, чтобы однозначно определить плоскость. Одним словом, красивая математическая лаконичность.

Казалось бы, плоскость можно однозначно определить с помощью двух неколлинеарных векторов. Но нет – векторы свободны и бродят по всему пространству, поэтому ещё нужна фиксированная точка:

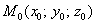
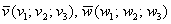
Уравнение плоскости, которая проходит через точку параллельно неколлинеарным векторам , выражается формулой:

! Примечание: под выражением «вектор параллелен плоскости» подразумевается, что вектор можно отложить и в самой плоскости. Для наглядности я буду откладывать векторы прямо в плоскости.

Принципиально ситуация выглядит так:
Обратите внимание, что точка и два коллинеарных вектора не определят плоскость однозначно (они будут «вертеться» вокруг точки и зададут целый «пучок» плоскостей).

Задача 130

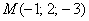
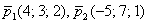
Составить уравнение плоскости по точке и неколлинеарным векторам .

Решение: искомое уравнение составим по формуле:

Определитель удобнее всего раскрыть по первому столбцу:

Раскрываем определители второго порядка:

На первом месте у нас нарисовался знак «минус», и хорошим тоном считается его убрать (точно так же, как и у общего уравнения «плоской» прямой).

Меняем у каждого слагаемого знак и проводим дальнейшие упрощения:

, сократить здесь ничего нельзя, поэтому:

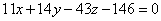
Ответ:

Как проверить задание? Для проверки пока не хватает информации, но мы обязательно выполним её чуть позже. Решаем самостоятельно:

Задача 131

Составить уравнение плоскости по векторам и принадлежащей ей точке .

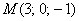
Кстати, если векторы коллинеарны, то и на этот случай есть корректный ответ 😉

Уравнения плоскости, компланарной двум неколлинеарным векторам

Напомним, что три или более векторов называются компланарными , если существует плоскость, которой они параллельны. Эту плоскость будем называть компланарной заданным векторам .

Направляющими векторами плоскости называются два неколлинеарных вектора, компланарных этой плоскости, т.е. принадлежащих плоскости или параллельных ей.

Пусть в координатном пространстве заданы:

б) два неколлинеарных вектора (рис.4.15).

Требуется составить уравнение плоскости, компланарной векторам и проходящей через точку

Выберем на плоскости произвольную точку . Обозначим — радиус-векторы точек и (рис.4.16).

Условие компланарности векторов (рис.4.16) можно записать, используя свойства смешанного произведения Применяя формулу (1.17), получаем уравнение плоскости, проходящей через заданную точку и компланарной двум неколлинеарным векторам:

Параметрическое уравнение плоскости

Пусть в координатном пространстве заданы:

б) два неколлинеарных вектора (рис.4.15).

Требуется составить параметрическое уравнение вида (4.10) плоскости, компланарной векторам и проходящей через точку

Выберем на плоскости произвольную точку . Обозначим -радиус-векторы точек и (рис.4.16).

Точка принадлежит заданной плоскости тогда и только тогда, когда векторы и компланарны (см. разд. 1.3.2). Запишем условие компланарности: где — некоторые действительные числа (параметры). Учитывая, что получим векторное параметрическое уравнение плоскости :

где — направляющие векторы плоскости, а — радиус-вектор точки, принадлежащей плоскости.

Координатная форма записи уравнения (4.19) называется параметрическим уравнением плоскости:

где и — координаты направляющих векторов и соответственно. Параметры в уравнениях (4.19),(4.20) имеют следующий геометрический смысл: величины пропорциональны расстоянию от заданной точки до точки принадлежащей плоскости. При точка совпадает с заданной точкой . При возрастании (или ) точка перемещается в направлении вектора (или ), а при убывании (или ) — в противоположном направлении.

1. Поскольку направляющие векторы плоскости неколлинеарны, то они ненулевые.

2. Любой вектор , коллинеарный плоскости, ортогонален нормальному вектору для этой плоскости. Поэтому их скалярное произведение равно нулю:

Следовательно, координаты и направляющих векторов и плоскости и ее нормали связаны однородными уравнениями:

3. Направляющие векторы плоскости определяются неоднозначно.

4. Для перехода от общего уравнения плоскости (4.15) к параметрическому (4.20) нужно выполнить следующие действия:

1) найти любое решение уравнения определяя тем самым координаты точки принадлежащей плоскости;

2) найти любые два линейно независимых решения однородного уравнения определяя тем самым координаты решения и направляющих векторов и плоскости;

3) записать параметрическое уравнение (4.20).

5. Чтобы перейти от параметрического уравнения плоскости к общему , достаточно либо записать уравнение (4.18) и раскрыть определитель, либо найти нормаль как результат векторного произведения направляющих векторов:

и записать общее уравнение плоскости в форме (4.14):

6. Векторное параметрическое уравнение плоскости (4.19), полученное в прямоугольной системе координат, имеет тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнении остается прежним.

Пример 4.8. В координатном пространстве (в прямоугольной системе координат) заданы точки и (см. рис.4.11). Требуется:

а) составить параметрическое уравнение плоскости, перпендикулярной отрезку и проходящей через его середину;

б) составить общее уравнение плоскости, проходящей через середину отрезка и компланарной радиус-векторам и

Решение. а) Общее уравнение искомой плоскости было получено в примере 4.5: Составим параметрическое уравнение:

1) находим любое решение уравнения , например, следовательно, точка принадлежит плоскости;

2) находим два линейно независимых (непропорциональных) решения однородного уравнения например и следовательно, векторы являются направляющими для плоскости;

3) записываем параметрическое уравнение плоскости (4.20):

б) Координаты середины отрезка были найдены в примере 4.5. Нормаль к искомой плоскости получим как векторное произведение ее направляющих векторов и

Составляем уравнение (4.14):

Тот же результат можно получить, записывая уравнение (4.18):