Уравнение плоскости, которая проходит через заданную прямую и заданную точку.
В этой статье собрана информация, необходимая для решения задачи составления уравнения плоскости, проходящей через заданную прямую и заданную точку. После решения этой задачи в общем виде мы приведем развернутые решения примеров на составление уравнения плоскости, которая проходит через заданную прямую и точку.
Навигация по странице.
Нахождение уравнения плоскости, проходящей через заданную прямую и заданную точку.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , задана прямая a и точка 

Сначала покажем, что существует единственная плоскость, уравнение которой нам требуется составить.
Напомним две аксиомы:
- через три различные точки пространства, не лежащие на одной прямой, проходит единственная плоскость;
- если две различные точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.
Из этих утверждений следует, что через прямую и не лежащую на ней точку можно провести единственную плоскость. Таким образом, в поставленной нами задаче через прямую a и точку M3 проходит единственная плоскость 
Теперь приступим к нахождению уравнения плоскости, проходящей через заданную прямую a и точку 
Если прямая a задана через указание координат двух различных точек М1 и М2 , лежащих на ней, то наша задача сводится к нахождению уравнения плоскости, проходящей через три заданные точки М1 , М2 и М3 .
Если же прямая a задана иначе, то нам сначала придется найти координаты двух точек М1 и М2 , лежащих на прямой a , а уже после этого записать уравнение плоскости, проходящей через три точки М1 , М2 и М3 , которое и будет искомым уравнением плоскости, проходящей через прямую a и точку М3 .
Разберемся, как найти координаты двух различных точек М1 и М2 , лежащих на заданной прямой a .
В прямоугольной системе координат в пространстве любой прямой линии соответствуют некоторые уравнения прямой в пространстве. Будем считать, что способ задания прямой a в условии задачи позволяет получить ее параметрические уравнения прямой в пространстве вида 




После этого нам останется лишь написать уравнение плоскости, проходящей через три различных и не лежащих на одной прямой точки 


Итак, мы получили уравнение плоскости, проходящей через заданную прямую a и заданную точку М3 , не лежащую на прямой a .
Примеры составления уравнения плоскости, проходящей через заданную точку и прямую.
Покажем решения нескольких примеров, в которых разберем рассмотренный метод нахождения уравнения плоскости, проходящей через заданную прямую и заданную точку.
Начнем с самого простого случая.
Напишите общее уравнение плоскости, которая проходит через координатную прямую Ox и точку 
Возьмем на координатной прямой Ox две различные точки, например, 

Теперь получим уравнение плоскости, проходящей через три точки М1 , М2 и М3 :
Это уравнение является искомым общим уравнением плоскости, проходящей через заданную прямую Ox и точку 

Если известно, что плоскость проходит через заданную точку и заданную прямую, и требуется написать уравнение плоскости в отрезках или нормальное уравнение плоскости, то следует сначала получить общее уравнение заданной плоскости, а от него переходить к уравнению плоскости требуемого вида.
Составьте нормальное уравнение плоскости, которая проходит через прямую 

Сначала напишем общее уравнение заданной плоскости. Для этого найдем координаты двух различных точек, лежащих на прямой 



Теперь мы можем составить общее уравнение прямой, проходящей через точку 

Осталось получить требуемый вид уравнения плоскости, умножив обе части полученного уравнения на нормирующий множитель 

Итак, нахождение уравнения плоскости, проходящей через заданную точку и заданную прямую, упирается в нахождение координат двух различных точек, лежащих на заданной прямой. В этом часто состоит основная сложность при решении подобных задач. В заключении разберем решение примера на составление уравнения плоскости, проходящей через заданную точку и прямую, которую определяют уравнения двух пересекающихся плоскостей.
В прямоугольной системе координат Oxyz задана точка 


Отталкиваясь от заданных уравнений двух пересекающихся плоскостей 

Процесс перехода от уравнений двух плоскостей, пересекающихся по прямой a , к параметрическим уравнениям прямой a подробно описан в статье уравнения прямой – уравнения двух пересекающихся плоскостей. Не будем на этом подробно останавливаться, а запишем лишь итоговый результат 




Таким образом, уравнение плоскости, проходящей через точку 


Уравнение плоскости, проходящей через точку и прямую онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через данную точку и через данную прямую (точка не лежит на этой прямой). Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямой (канонический или параметрический) введите координаты точки и коэффициенты уравнения прямой в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости, проходящей через точку и прямую − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L:
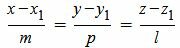 . . | (1) |
Задача заключается в построении уравнения плоскости α, проходящей через точку M0 и и через прямую L(Рис.1).
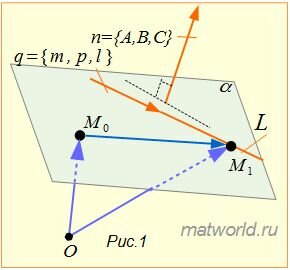 |
Решение. Уравнение плоскости, проходящей через точку M0 и имеющий нормальный вектор n=<A, B, C> имеет следующий вид:
| A(x−x0)+B(y−y0)+C(z−z0)=0. | (2) |
Направляющий вектор прямой L имеет вид q=<m, p, l>. Поскольку плоскость проходит через прямую L, то она проходит также через точку M1(x1, y1, z1). Тогда уравнение плоскости, проходящей через точку M1(x1, y1, z1) имеет вид:
| A(x−x1)+B(y−y1)+C(z−z1)=0. | (3) |
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q прямой L, т.е. скалярное произведение этих векторов должен быть равным нулю:
Вычитая уравнение (3) из уравнения (2), получим:
| A(x1−x0)+B(y1−y0)+C(z1−z0)=0. | (5) |
Решая совместно уравнения (4) и (5) отностительно коэффициентов A, B, C получим такие значения A, B, C, при которых уравнение (2) проходит через точку M0 и через прямую (1). Для решения систему уравнений (4), (5), запишем их в матричном виде:
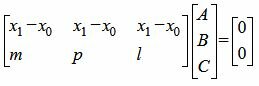 . . | (6) |
Как решить систему линейных уравнений посмотрите на странице метод Гаусса онлайн.
Получив частное решение уравнения (6) и подставив полученные значения A, B, C в (2), получим решение задачи.
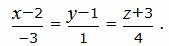 | (7) |
Решение. Уравнение плоскости α, проходящей через точку M0(x0, y0, z0)=M0(1, 2, 5) и имеющий нормальный вектор n=<A, B, C> представляется формулой (2).
Вычитая уравнение (3) из уравнения (2), получим:
| A(x1−x0)+B(y1−y0)+C(z1−z0)=0. | (8) |
Направляющий вектор прямой L имеет следующий вид:
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q прямой L, т.е. скалярное произведение этих векторов должен быть равным нулю:
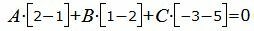 | (10) |
 | (11) |
Решим систему линейных уравнений (10) и (11) отностительно A, B, C. Для этого представим эти уравнения в матричном виде:
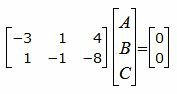 | (12) |
Решив однородную систему линейных уравнений (12) используя метод Гаусса, найдем следующее частное решение:
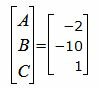 |
Подставляя значения коэффициентов A, B, C в уравнение плоскости (2), получим:
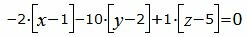 | (13) |
Упростим уравнение (13):
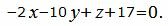 | (14) |
Ответ: Уравнение плоскости, проходящей через точку M0(1, 2, 5) и через прямую (7) имеет вид (14).
Пример 2. Найти уравнение плоскости α, проходящую через точку M0(4, 3, −6) и через прямую L, заданной параметрическим уравнением:
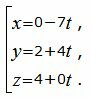 | (15) |
Решение. Приведем параметрическое уравнение (15) к каноническому виду:
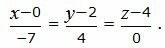 | (16) |
Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n=<A, B, C> представляется формулой:
| A(x−x0)+B(y−y0)+C(z−z0)=0. | (17) |
Поскольку плоскость проходит через прямую L, то она проходит также через точку M1(x1, y1, z1)=(0, 2, 4). Тогда уравнение плоскости, проходящей через точку M1(x1, y1, z1) имеет вид:
| A(x−x1)+B(y−y1)+C(z−z1)=0. | (18) |
Вычитая уравнение (18) из уравнения (17), получим:
| A(x1−x0)+B(y1−y0)+C(z1−z0)=0. | (19) |
Направляющий вектор прямой L имеет следующий вид:
Для того, чтобы плоскость проходила через прямую L, нормальный вектор плоскости n должен быть ортогональным направляющему вектору прямой L :
| Am+Bp+Cl=0. | (20) |
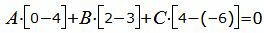 | (21) |
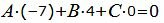 | (22) |
Решим систему линейных уравнений (21) и (22) отностительно A, B, C. Для этого представим эти уравнения в матричном виде:
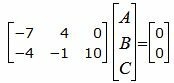 | (23) |
Решив однородную систему линейных уравнений (23) используя метод Гаусса, найдем следующее частное решение:
 |
Подставляя значения коэффициентов A, B, C в уравнение плоскости (17), получим:
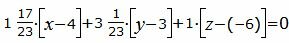 | (24) |
Упростим уравнение (24):
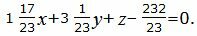 | (25) |
Уравнение плоскости можно представить более упрощенном виде, умножив на число 23.
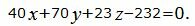 | (26) |
Ответ: Уравнение плоскости, проходящей через точку M0(4, 3, −6) и через прямую (16) имеет вид (26).
Уравнение плоскости, виды уравнения плоскости
В предыдущем разделе, посвященном плоскости в пространстве, мы рассмотрели вопрос с позиции геометрии. Теперь же перейдем к описанию плоскости с помощью уравнений. Взгляд на плоскость со стороны алгебры предполагает рассмотрение основных видов уравнения плоскости в прямоугольной системе координат O х у z трехмерного пространства.
Определение уравнения плоскости
Плоскость – это геометрическая фигура, состоящая из отдельных точек. Каждой точке в трехмерном пространстве соответствуют координаты, которые задаются тремя числами. Уравнение плоскости устанавливает зависимость между координатами всех точек.
Уравнение плоскости в прямоугольной системе координат 0хуz имеет вид уравнения с тремя переменными х , у и z . Удовлетворяют уравнению координаты любой точки, лежащей в пределах заданной плоскости, не удовлетворяют координаты любых других точек, которые лежат вне заданной плоскости.
Подстановка в уравнение плоскости координат точки данной плоскости, обращает уравнение в тождество. При подстановке координат точки, лежащей вне плоскости, уравнение превращается в неверное равенство.
Уравнение плоскости может иметь несколько видов. В зависимости от специфики решаемых задач уравнение плоскости может быть записано по-разному.
Общее уравнение плоскости
Сформулируем теорему, а затем запишем уравнение плоскости.
Всякая плоскость в прямоугольной системе координат O x y z в трехмерном пространстве может быть задана уравнением вида A x + B y + C z + D = 0 , где А , В , С и D – некоторые действительные числа, которые одновременно не равны нулю. Всякое уравнение, имеющее вид A x + B y + C z + D = 0 , определяет плоскость в трехмерном пространстве
Уравнение, имеющее вид A x + B y + C z + D = 0 носит название общего уравнения плоскости. Если не придавать числам А , В , С и D конкретных значений, то мы получаем уравнение плоскости в общем виде.
Важно понимать, что уравнение λ · A x + λ · B y + λ · C z + λ · D = 0 , будет точно так же определять плоскость. В уравнении λ — это некоторое отличное от нуля действительное число. Это значит, что равенства A x + B y + C z + D = 0 и λ · A x + λ · B y + λ · C z + λ · D = 0 равнозначны.
Общим уравнениям плоскости x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 удовлетворяют координаты одних и тех же точек, расположенных в трехмерном пространстве. Это значит, что они задают одну и ту же плоскость.
Дадим пояснения к рассмотренной выше теореме. Плоскость и ее уравнение неразделимы, так как каждому уравнению A x + B y + C z + D = 0 соответствует плоскость в заданной прямоугольной системе координат, а каждой плоскости, расположенной в трехмерном пространстве, соответствует ее уравнение вида A x + B y + C z + D = 0 .
Уравнение плоскости A x + B y + C z + D = 0 может быть полным и неполным. Все коэффициенты А , B , С и D в полном уравнении отличны от нуля. В противном случае, общее уравнение плоскости считается неполным.
Плоскости, которые задаются неполными уравнениями, могут быть параллельны координатным осям, проходить через оси координат, совпадать с координатными плоскостями или располагаться параллельно им, проходить через начало координат.
Рассмотрим положение в пространстве плоскости, заданной уравнением 4 · y — 5 · z + 1 = 0 .
Она параллельна оси абсцисс и располагается перпендикулярно по отношению к плоскости O y z . Уравнение z = 0 определяет координатную плоскость O y z , а общее уравнение плоскости вида 3 · x — y + 2 · z = 0 соответствует плоскости, которая проходит через начало координат.
Важное уточнение: коэффициенты А , В и С в общем уравнении плоскости представляют собой координаты нормального вектора плоскости.
Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости. Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости.
Нормальное уравнение плоскости
Нормальное уравнение плоскости – это общее уравнение плоскости вида A x + B y + C z + D = 0 , которое удовлетворяет следующим условиям: длина вектора n → = ( A , B , C ) равна единице, т.е. n → = A 2 + B 2 + C 2 = 1 , а D ≤ 0 .
Также запись нормального уравнения плоскости может иметь следующий вид cos α · x + cos β · y + cos γ · z — p = 0 , где p – это неотрицательное число, которое равно расстоянию от начала координат до плоскости, а cos α , cos β , cos γ — это направляющие косинусы нормального вектора данной плоскости единичной длины.
n → = ( cos α , cos β , cos γ ) , n → = cos 2 α + cos 2 β + cos 2 γ = 1
То есть, согласно нормальному уравнению плоскости, плоскость в прямоугольной системе координат O х у z удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости n → = ( cos α , cos β , cos γ ) . Если p равно нулю, то плоскость проходит через начало координат.
Плоскость задана общим уравнением плоскости вида — 1 4 · x — 3 4 · y + 6 4 · z — 7 = 0 . D = — 7 ≤ 0 , нормальный вектор этой плоскости n → = — 1 4 , — 3 4 , 6 4 имеет длину, равную единице, так как n → = — 1 4 2 + — 3 4 2 + 6 4 = 1 . Соответственно, это общее уравнение плоскости является нормальным уравнением плоскости.
Для более детального изучения нормального уравнения плоскости мы рекомендуем перейти в соответствующий раздел. В теме приведены разборы задач и характерные примеры, а также способы приведения общего уравнения плоскости к нормальному виду.
Уравнение плоскости в отрезках
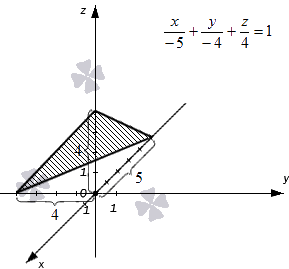
Плоскость отсекает на координатных осях O х , O у и O z отрезки определенной длины. Длины отрезков задаются отличными от нуля действительными числами a , b и с . Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 . Знак чисел а , b и с показывает, в каком направлении от нулевого значения следует откладывать отрезки на координатных осях.
Построим в прямоугольной системе координат плоскость, которая задана уравнением формулы плоскости в отрезках x — 5 + y — 4 + z 4 = 1 .
Точки удалены от начала координат в отрицательном направлении на 5 единиц по оси абсцисс, на 4 единицы в отрицательном направлении по оси ординат и на 4 единицы в положительном направлении по оси аппликат. Отмечаем точки и соединяем их прямыми линиями.
Плоскость полученного треугольника является плоскостью, соответствующей уравнению плоскости в отрезках, имеющего вид x — 5 + y — 4 + z 4 = 1 .
Более подробно информация об уравнении плоскости в отрезках, приведении уравнения плоскости в отрезках к общему уравнению плоскости размещена в отдельной статье. Там же приведен ряд решений задач и примеров по теме.
http://matworld.ru/analytic-geometry/uravnenie-ploskosti4-online.php
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenie-ploskosti-vidy-uravnenija-ploskosti/