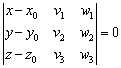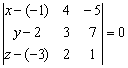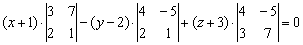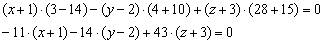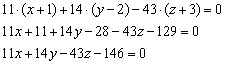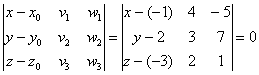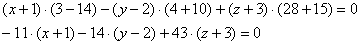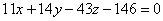Составить уравнение плоскости по вектору и точек

Онлайн калькулятор. Уравнение плоскости

Предлагаю вам воспользоваться онлайн калькулятором чтобы найти уравнение плоскости.

Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения плоскости и закрепить пройденный материал.

Найти уравнение плоскости

Выберите метод решения исходя из имеющихся в задаче данных:

В задаче известны:

Ввод данных в калькулятор для составления уравнения плоскости

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления уравнения плоскости

• Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.

Теория. Уравнение плоскости.

Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки

В зависимости от условий задачи уравнение плоскости можно составить следующими способами:

Если заданы координаты трех точек A( x ₁, y ₁, z ₁), B( x ₂, y ₂, z ₂) и C( x ₃, y ₃, z ₃), лежащих на плоскости, то уравнение плоскости можно составить по следующей формуле

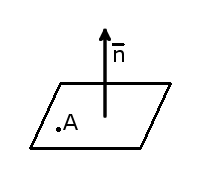
Если заданы координаты точки A( x ₁, y ₁, z ₁) лежащей на плоскости и вектор нормали n = , то уравнение плоскости можно составить по следующей формуле:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Как составить уравнение плоскости по точке и двум неколлинеарным векторам?

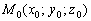
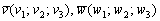
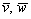
Рассмотрим точку и два неколлинеарных вектора .Уравнение плоскости, которая проходит через точку параллельно векторам ,выражается формулой:

! Примечание: под выражением «вектор параллелен плоскости» подразумевается, что вектор можно отложить и в самой плоскости. Для наглядности я буду откладывать векторы прямо в плоскости.

Принципиально ситуация выглядит так:

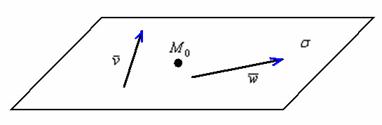
Обратите внимание, что точка и два коллинеарных вектора не определят плоскость (векторы будут свободно «вертеться» вокруг точки).

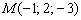
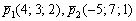
Составить уравнение плоскости по точке и векторам .

Решение: Составим уравнение плоскости по точке и двум неколлинеарным векторам:

Определитель удобнее всего раскрыть по первому столбцу:

Раскрываем определители второго порядка:

На первом месте у нас находится знак «минус». Хорошим тоном считается убрать наглеца, в этих целях меняем знак у каждого слагаемого. Проводим дальнейшие упрощения и получаем уравнение плоскости:

Сократить здесь ничего нельзя, поэтому:

Ответ:

…числа, конечно, страшноваты получились для первого примера =) …но переделывать, пожалуй, не буду, на практике большие числа – вещь распространённая.

Как проверить задание? Для проверки пока не хватает информации, но я обязательно выполню её чуть позже.

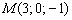
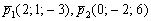
Составить уравнение плоскости по точке и двум неколлинеарным векторам .

Это пример для самостоятельного решения, полное решение и ответ в конце урока.

Иногда может потребоваться решить обратную задачу – по известному уравнению плоскости найти параллельные ей векторы. Кстати, сколько параллельных векторов существует у плоскости? Бесконечно много. Однако нельзя объять необъятное, поэтому «вытащим» из уравнения плоскости три таких вектора:

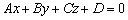
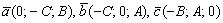
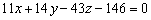
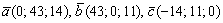
Пусть плоскость задана общим уравнением . Тогда векторы будут параллельны данной плоскости (а, значит,компланарны), и какие-либо два из них – линейно независимы. Так, в Примере №1 мы составили уравнение плоскости . Построенной плоскости будут параллельны следующие векторы: . Если честно, не припомню, чтобы приходилось этим пользоваться, тем не менее, справка не лишняя.

Два неколлинеарных вектора и точка – это «жёсткая» конструкция, однозначно определяющая плоскость. Но существует более очевидный способ, о котором упоминалось выше, и он громким стуком в дверь уже давно просится на урок. Три точки. Дёшево и сердито.

5.2.1. Как составить уравнение плоскости
по точке и двум неколлинеарным векторам?

Конструировать уравнение будем с помощью векторов и точек. Их должно быть как можно меньше, но достаточно, чтобы однозначно определить плоскость. Одним словом, красивая математическая лаконичность.

Казалось бы, плоскость можно однозначно определить с помощью двух неколлинеарных векторов. Но нет – векторы свободны и бродят по всему пространству, поэтому ещё нужна фиксированная точка:

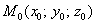
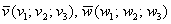
Уравнение плоскости, которая проходит через точку параллельно неколлинеарным векторам , выражается формулой:

! Примечание: под выражением «вектор параллелен плоскости» подразумевается, что вектор можно отложить и в самой плоскости. Для наглядности я буду откладывать векторы прямо в плоскости.

Принципиально ситуация выглядит так:
Обратите внимание, что точка и два коллинеарных вектора не определят плоскость однозначно (они будут «вертеться» вокруг точки и зададут целый «пучок» плоскостей).

Задача 130

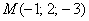
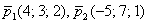
Составить уравнение плоскости по точке и неколлинеарным векторам .

Решение: искомое уравнение составим по формуле:

Определитель удобнее всего раскрыть по первому столбцу:

Раскрываем определители второго порядка:

На первом месте у нас нарисовался знак «минус», и хорошим тоном считается его убрать (точно так же, как и у общего уравнения «плоской» прямой).

Меняем у каждого слагаемого знак и проводим дальнейшие упрощения:

, сократить здесь ничего нельзя, поэтому:

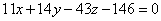
Ответ:

Как проверить задание? Для проверки пока не хватает информации, но мы обязательно выполним её чуть позже. Решаем самостоятельно:

Задача 131

Составить уравнение плоскости по векторам и принадлежащей ей точке .

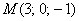
Кстати, если векторы коллинеарны, то и на этот случай есть корректный ответ 😉