Проекции векторов на прямую и на плоскость
Проекция вектора на прямую
Пусть на плоскости задана прямая и пересекающая ее прямая . Проекцией вектора на прямую параллельно прямой (вдоль прямой ) называется вектор , началом которого служит проекция , начала , а концом — проекция конца вектора (рис.1.13,а). Если прямая перпендикулярна прямой , то проекция называется ортогональной.
Пусть в пространстве дана прямая и пересекающая ее плоскость . Проекцией вектора на прямую параллельно плоскости (вдоль плоскости ) называется вектор , началом которого служит проекция , начала , а концом — проекция конца вектора (рис. 1.13,6). Если плоскость перпендикулярна прямой , то проекция называется ортогональной.
Проекция вектора на плоскость
Пусть в пространстве задана плоскость я и пересекающая ее прямая . Проекцией вектора на плоскость параллельно прямой (вдоль прямой ) называется вектор , началом которого служит проекция начала , а концом — проекция конца вектора (рис. 1.14). Если прямая перпендикулярна плоскости , то проекция называется ортогональной.
Свойства проекций векторов
1. Проекции вектора на параллельные прямые (или на параллельные плоскости) равны.
2. Проекции равных векторов равны.
3. Проекция суммы векторов равна сумме их проекций.
4. Проекция произведения вектора на число равна произведению этого числа на проекцию вектора, другими словами, отношение коллинеарных векторов равно отношению их проекций (если оно определено).
5. Проекция линейной комбинации векторов равна линейной комбинации проекций.
Рассмотрим эти свойства для проекций векторов на прямую параллельно прямой . Для проекций векторов на плоскость или на прямую параллельно плоскости доказательства аналогичные.
Докажем первое свойство. Пусть — проекция вектора на прямую вдоль прямой , а — проекция вектора на прямую вдоль той же прямой , причем прямые и параллельные (рис. 1.15). Четырехугольник, образованный пересечением пары параллельных прямых и штриховыми линиями, параллельными прямой , является параллелограммом. Следовательно, , т.е. проекции одного и того же вектора на параллельные прямые равны.
Докажем второе свойство. Пусть на плоскости даны равные векторы и , не параллельные прямой (см. рис. 1.16). Построим равные им векторы и . Из равенства следует, что четырехугольник — параллелограмм, а треугольники и равны по стороне и двум прилежащим углам
как углы с соответственно параллельными сторонами). Следовательно, , т.е. равные векторы, не параллельные прямой , имеют равные проекции. Если же векторы параллельны прямой , то их проекции также равны, как нулевые векторы. Второе свойство доказано.
Доказательство третьего свойства очевидно для векторов и (рис. 1.17): проекция вектора равна сумме проекций и , векторов и , т.е. . Для произвольных векторов и (у которых конец вектора не совпадает с началом вектора ) доказательство сводится к рассмотренному случаю для равных им векторов и , так как равные векторы имеют равные проекции (по второму свойству).
Доказательство четвертого свойства следует из теоремы Фалеса (см. разд. В.2). На рис.1.18 изображены векторы и 0)» png;base64,iVBORw0KGgoAAAANSUhEUgAAAEAAAAAWBAMAAACCkIcHAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAvWZBmjHwIdCB4BFRAWKYcvQAAAFOSURBVCjPY2AgDHgm4JK5EgCmAjcwcAphSPIaX2DgXgpicS8G8vwU0BWEuQDFLUAsTgEgUSeAJs+exHCugOEWSN+1A0CC4zVYOKQApoDlLQObAwPTWiDz3AYgwfQILMwsEgBVwNHLcHEtA+tTIHPGBSBx+8UFiApBW4iCe7IMF98y8CYBmYJgATmo4eyOtjAFjE8ZeIGSvCJgAT0HqO+ue+mCaDsBBsbHYN28K0F8pmVrYc67PQPk6n1QBRcYeDtBomohj2EKuMEKQFYAfeZ4AWIF02OeJ7AAmAG24lYvA2MuxIEgrKfAuwziDXYPSJheecBwTQDsSJA3mYDa/UAGM7BCPcHA+obBzoCBNxPk3g0M9xyggQ0PBqCrlIBhwA5y2a0DDKwgsw1QgpqBXQnIZsqFRRYOcAOUVLhTcSuwgiQYnPLcrQSSHIsBESkWAKi0S8GJu/2KAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />, а также их проекции и . По теореме Фалеса , следовательно, , что и требовалось доказать. В случае доказательство аналогичное.
Пятое свойство проекций следует из третьего и четвертого.
Теорема 1.1 (о проекциях вектора на пересекающиеся прямые).
1. Если на плоскости заданы две пересекающиеся прямые и , то любой вектор на плоскости можно однозначно представить в виде суммы своих проекций и на эти прямые (проекции на каждую прямую берутся вдоль другой прямой), т.е. .
2. Если в пространстве заданы три прямые и , пересекающиеся в одной точке и не лежащие в одной плоскости, то любой вектор в пространстве можно однозначно представить в виде суммы своих проекций на эти прямые (проекции на каждую прямую берутся вдоль плоскости, содержащей две другие прямые), т.е. .
В самом деле, пусть прямые и пересекаются в точке (рис.1.19,а). Приложим вектор к точке , т.е. рассмотрим вектор . По правилу параллелограмма сложения векторов (см. разд. 1.2) получаем равенство , которое равносильно доказываемому равенству , так как равные векторы имеют равные проекции (см. свойство 2 проекций). Единственность представления следует из однозначности нахождения проекций вектора.
Если же вектор коллинеарен одной из прямых, например , то соответствующие проекции имеют вид: и равенство , очевидно, выполняется.
Аналогично доказывается второе утверждение.
Справедливы утверждения, обратные к указанным в теореме 1.1.
Если вектор на плоскости равен сумме двух неколлинеарных векторов, т.е. , то слагаемые и являются проекциями вектора на прямые, содержащие векторы и соответственно.
Если вектор в пространстве равен сумме трех некомпланарных векторов, т.е. , то слагаемые и являются проекциями вектора на прямые, содержащие векторы соответственно.
В самом деле, отложим от произвольной точки векторы (рис.1.19,6). Тогда из равенства следует, что , т.е. вектор — является диагональю параллелепипеда, построенного на векторах (отсюда следует правило параллелепипеда сложения трех некомпланарных векторов). Поэтому — проекции вектора на прямые (проекция на каждую прямую берется вдоль плоскости, проходящей через две другие прямые). Так как равные векторы и имеют равные проекции (свойство 2), заключаем, что проекции вектора на прямые равны соответственно. Наконец, проекции на прямые равны проекциям на параллельные им прямые, содержащие векторы соответственно.
Пример 1.5. Если прямая пересекает стороны треугольника (или их продолжения) в точках соответственно, то
Решение. Найдем отношения проекций векторов на прямую вдоль прямой (рис. 1.20). Для этого через точку проведем прямую , параллельную прямой . По свойству 4 проекций имеем:
Перемножая эти пропорции, получаем , что равносильно доказываемому равенству.
Заметим, что доказанное утверждение является частью теоремы Менелая.
Пример 1.6. Если на сторонах треугольника взяты соответственно точки так, что прямые пересекаются в одной точке, то
Решение. Пусть прямые пересекаются в точке (рис.1.21). Через точку проведем прямые и параллельно и соответственно. По свойству проекций (свойство 4):
Учитывая эти равенства и свойства отношений коллинеарных векторов (см, разд.1.2.1), преобразуем левую и правую части последнего равенства:
Запишем произведение правых частей этих равенств, учитывая, что произведение левых частей равно единице:
Найдем обратное отношение , что и требовалось доказать.
Заметим, что доказанное утверждение является частью теоремы Чевы.
ПАРАЛЛЕЛЬНАЯ И ЦЕНТРАЛЬНАЯ ПРОЕКЦИИ
| Добавил: | DMT |
| Дата создания: | 28 июня 2008, 22:41 |
| Дата обновления: | 28 июня 2008, 22:42 |
| Просмотров: | 20969 последний сегодня, 5:18 |
| Комментариев: | 0 |
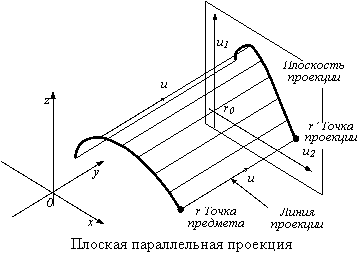
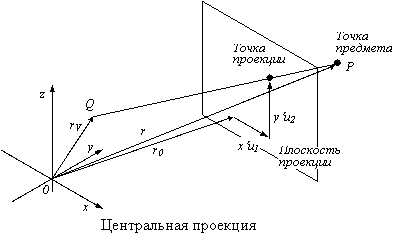
ПАРАЛЛЕЛЬНАЯ И ЦЕНТРАЛЬНАЯ ПРОЕКЦИИ Для изображения лежащих в трехмерном пространстве объектов координаты точек (мировые координаты) преобразуются сначала в координаты в пространстве изображения, а затем – в экранные. Для произвольных трехмерных векторов a , b и c через (a,b,c) обозначим смешанное произведение. Скалярное произведение векторов будем обозначать через a ? b , векторное – через a ? b . Пусть наблюдатель находится в точке (x V ,y V ,z V ) . Центральной проекцией произвольной точки (x,y,z) называется точка пересечения плоскости проекции и луча, соединяющего точку (x V ,y V ,z V ) наблюдения с точкой (x,y,z) . Параллельная проекция получается из центральной, если точку наблюдения бесконечно удалить в некотором направлении. Рассмотрим, например, шар в трехмерном пространстве. Соединяя точку наблюдения (x V ,y V ,z V ) с каждой точкой шара, мы получим круговой конус. Так как пересечение произвольной плоскости с конусом является эллипсом, то центральной проекцией шара будет эллипс, превращающийся в круг только в тех случаях, когда плоскость проекции перпендикулярна прямой, проходящей через точку наблюдения и центр шара. Опишем формулы преобразования координат при параллельной и центральной проекции. Параллельная проекция. Пусть задана декартова система координат (x,y,z) . Рассмотрим произвольную плоскость P , проходящую через некоторую точку (x 0 ,y 0 ,z 0 ) , радиус-вектор которой равен r 0 , параллельно векторам u 1 и u 2 (рис.) .
Пусть u – произвольный вектор. Тогда для каждой точки r трехмерного пространства существует единственная тройка (x’,y’,z’) вещественных чисел такая, что r=r 0 +x’u 1 +y’u 2 +z’u . Пару чисел (x’,y’) мы будем называть координатами параллельной проекции точки (x,y,z) на плоскость P вдоль направления u , или параллельной проекцией на плоскость P параллельно вектору u (рис) .
Чтобы найти x’ , y’ и z’ , умножим обе части равенства r-r 0 =x’u 1 +y’u 2 +z’u скалярно на векторы, выбранные таким образом, что в правой части остается лишь один ненулевой член. Умножая на u 1 ? u , приходим к равенству (r-r 0 ,u 1 ,u) = y'(u 2 ,u 1 ,u) . Умножая на u 2 ? u , получим (r-r 0 ,u 2 ,u) = x'(u 1 ,u 2 ,u) . Наконец, скалярное произведение на u 1 ? u 2 приводит к равенству (r–r 0 ,u 1 ,u 2 ) = z'(u,u 1 ,u 2 ) . Отсюда вытекает, что координаты (x’,y’) проекции вдоль направления u на плоскость P можно вычислить с помощью формул x’=(r-r 0 ,u 2 ,u)/(u 1 ,u 2 ,u) , y’=-(r-r 0 ,u 1 ,u)/(u 1 ,u 2 ,u) . При применении алгоритмов удаления невидимых линий необходимо знать координату, характеризующую степень удаленности точки от плоскости P . Согласно выкладкам, эта координата равна z’=(r-r 0 ,u 1 ,u 2 )/(u 1 ,u 2 ,u) . Пример 3.1. Рассмотрим параллельную проекцию трехмерного пространства на плоскость Oyz в направлении вектора u=(1,0.7,0.7) . Плоскость Oyz можно задать векторами u 1 =(0,1,0) , u 2 =(0,0,1) . Смешанное произведение (u 1 ,u 2 ,u) равно 1 . Поэтому
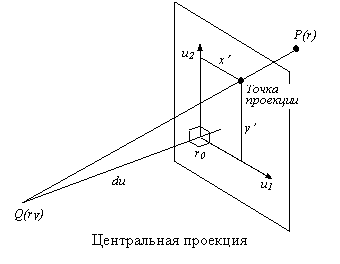
отсюда находим x’=-0.7x+y , y’=-0.7x+z . Пример 3.2. Рассмотрим ортогональную проекцию на плоскость, проходящую через начало координат, заданную единичным вектором нормали n . В этом случае u=n . Вектор u 1 , обычно, (например, в архитектуре или в военном деле) берут лежащим в горизонтальной плоскости Oxy . Этот вектор должен быть ортогонален вектору u , поэтому при u 1 = < x , h ,0>выполнено соотношение x u x + h u y =0 . Решая это уравнение получаем u 1 , а затем u 2 : Центральная проекция . Пусть задана плоскость с началом координат r 0 и базисными векторами u 1 и u 2 (рис.). Требуется изобразить на плоскости проекцию точки r=(x,y,z) из точки наблюдения r V . Пусть (x’,y’) – искомые координаты. Тогда для некоторого l I R выполнено равенство r 0 +x’u 1 +y’u 2 =r V + l (r-r V ) . Координаты x’ , y’ будут вычисляться по формулам x’=(r V -r 0 , u 2 , r-r V )/(u 1 , u 2 , r-r V ) ,
y’=(r V -r 0 , u 1 , r-r V )/(u 1 , u 2 , r-r V ). Число l характеризует дальность точки r , в частности при l точка r лежит перед плоскостью, а при l >1 – за плоскостью проекции, l =-(r V -r 0 , u 1 ,u 2 )/(u 1 , u 2 , r-r V ) (ближе всех лежат точки, для которых l =0 ). Если (u 1 , u 2 , r V -r 0 )>0 , то в качестве третьей координаты z’ , чтобы система координат (x’,y’,z’) была правой, берется значение z’=- l . Поскольку l > 0 , для всех лежащих в поле зрения наблюдателя точек r , то координата z’ будет меньше нуля. Укажем теперь, как можно получить центральную проекцию из параллельной. Пусть u – произвольный вектор, коллинеарный вектору r V -r 0 . Тогда существует число d такое, что r V –r 0 =du . Рассмотрим проекцию, параллельную вектору u , на плоскость, заданную векторами r 0 , u 1 и u 2 . Предположим, что координаты параллельной проекции точки (x,y,z) вдоль вектора u равны (x»,y»,z») . Тогда x»=(r-r 0 , u 2 , u)/(u 1 , u 2 , u), y»=-(r-r 0 , u 1 , u)/(u 1 , u 2 , u), z»=(r-r 0 , u 1 , u 2 )/(u 1 , u 2 , u). Подставляя приведенные выше для центральной проекции формулы, убеждаемся в том, что координаты центральной проекции будут вычисляться по следующим формулам: справедливость которых легко проверить аналогично, исходя из геометрических соображений. При применении алгоритмов удаления невидимых линий полагают, что ось z’ перпендикулярна плоскости (x’,y’) , а числа x’ и y’ служат координатами проекции. Обычно вектор r 0 выбирают так, чтобы прямая, соединяющая точку r V с точкой r 0 , была перпендикулярна плоскости проекции (рис.) . В этом случае r V -r 0 =du , где u=u 1 ? u 2 , а d – расстояние от точки r V до плоскости, поэтому
x’=-d(r-r 0 ) ? u 1 / ((r-r 0 ) ? u — d) ; y’=-d(r-r 0 ) ? u 2 / ((r-r 0 ) ? u — d) ; z’=- l =d/((r-r 0 ) ? u — d) . Пример 3.3. Пусть ось Oz параллельна плоскости проекции. Положим u 2 =(0,0,1) . Рассмотрим единичный вектор u 1 , перпендикулярный вектору u 2 , лежащий в плоскости проекции. Положим u=u 1 ? u 2 . Выберем так вектор r 0 , чтобы вектор r 0 -r V был перпендикулярен плоскости проекции. Тогда r 0 =r V -d(u 1 ? u 2 ) , где d – расстояние от точки наблюдения до плоскости проекции. Вектор u лежит в плоскости Oxy , поэтому существует некоторый угол a такой, что u=(cos a , sin a , 0) . Выберем третьим вектор u 1 =(-sin a , cos a , 0) , этот вектор перпендикулярен векторам u 2 и u , и имеет единичную длину. Если предположить, что координаты точки наблюдения равны (x V ,y V ,z V ) , то координаты центральной проекции точки (x,y,z) будут вычисляться по формулам x’=-d((x-x V )(-sin a )+(y-y V )cos a )/((x-x V )cos a +(y-y V )sin a ) ; y’=-d(z-z V )/((x-x V )cos a +(y-y V )sin a ) ; z’=- l =d/((x-x V )cos a +(y-y V )sin a ) . 5.2.1. Как составить уравнение плоскости | |
, 
,
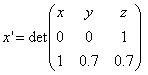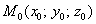параллельно неколлинеарным векторам 
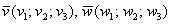, выражается формулой: 
Обратите внимание, что точка и два коллинеарных вектора не определят плоскость однозначно (они будут «вертеться» вокруг точки и зададут целый «пучок» плоскостей).
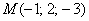и неколлинеарным векторам 
.
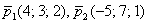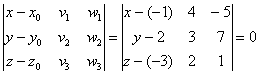
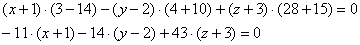
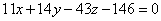, сократить здесь ничего нельзя, поэтому: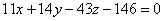
и принадлежащей ей точке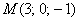 
.