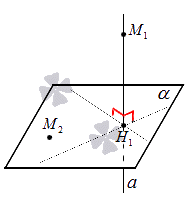
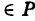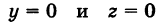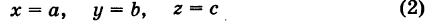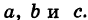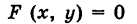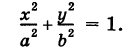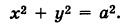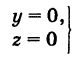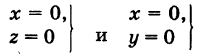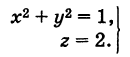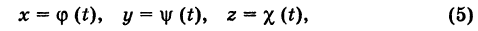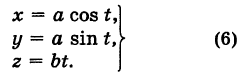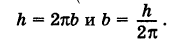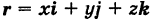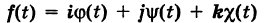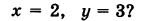Задача 31787 Найти проекцию прямой (x–2)/5 = (y–3)/1.
Условие
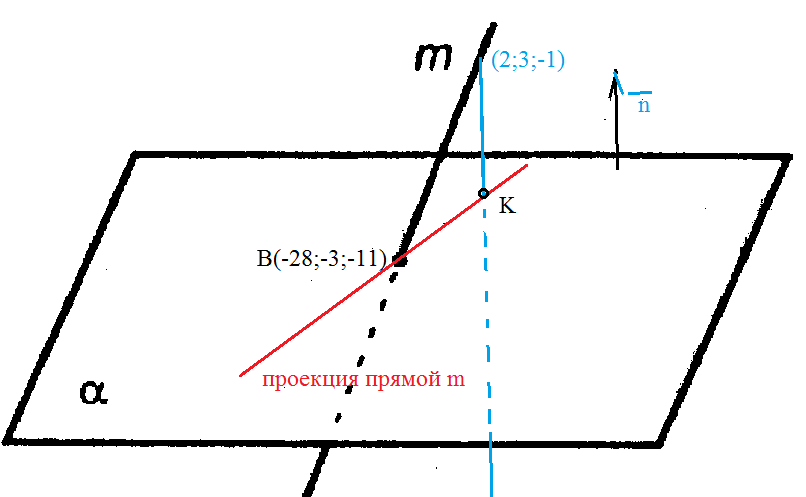
Найти проекцию прямой (x–2)/5 = (y–3)/1 = (z+1)/2 на плоскость x+4y–3z+7=0
Решение
Точка (2;3;-1) принадлежит данной прямой.
Составим уравнение прямой || нормальному вектору плоскости
vector
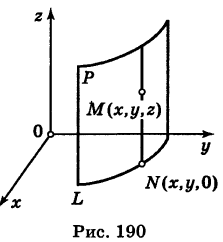
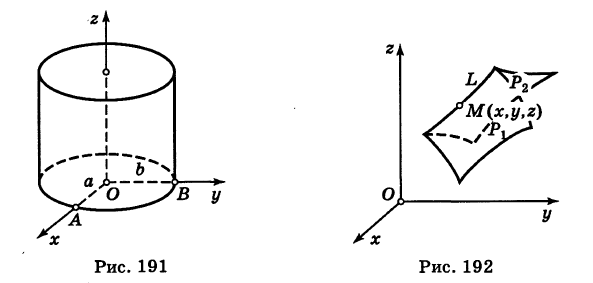
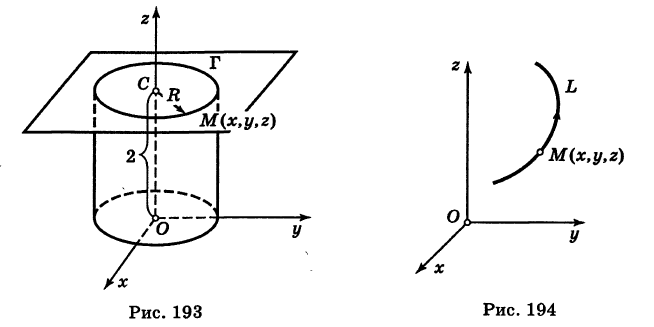
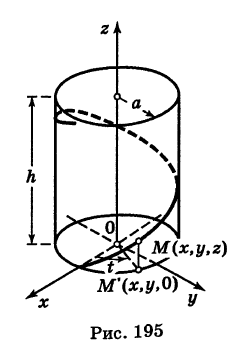
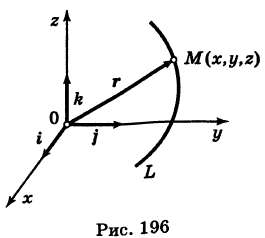
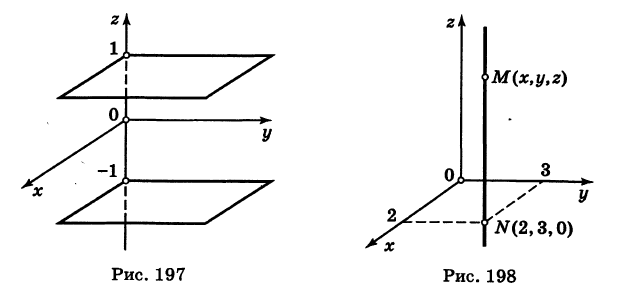
Найдем координаты точки K — точки пересечения этой прямой и плоскости Обозначим отношение подставим в уравнение плоскости Найдем координаты точки В — точки пересечения данной прямой и данной плоскости. Обозначим отношение подставим в уравнение плоскости Составляем уравнение прямой ВК, как уравнение прямой, проходящей через две точки Содержание: Определение: Уравнение м поверхности в пространстве Oxyz называется такое уравнение между переменными х, у у z, которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности. То есть если — уравнение поверхности Р (рис. 189), то при М(х, у, z) Таким образом, уравнение (1) выполнено тогда и только тогда, когда точка М(х, у, z) принадлежит данной поверхности. Координаты произвольной точки поверхности называются текущими координатами точки. Поэтому составить уравнение поверхности — это значит найти связь между текущими координатами ее точек. Пример (уравнения координатных плоскостей): Каждая точка М(х, у, z), лежащая на координатной плоскости Oyz, имеет абсциссу х = 0; обратно, если для какой-нибудь точки М(х, у, z) абсцисса ее х = 0, то эта точка расположена на плоскости Oyz. Следовательно, — уравнение координатной плоскости Oyz. Аналогично, — соответственно уравнения координатных плоскостей Oxz и Оху. Формула В более общем случае — уравнения трех плоскостей, перпендикулярных соответствующим координатным осям Ох, Оу, Ог и отсекающих на них отрезки, численно равные Теорема: Уравнение цилиндрической поверхности, образующие которой параллельны координатной оси, не содержит текущей координаты, одноименной с этой координатной осью, и обратно. Доказательство: Пусть, например, цилиндрическая поверхность Р образована перемещением прямой Обозначим через М(х, у, z) точку поверхности Р с текущими координатами х, у и z. Образующая MN, проходящая через точку М, пересекает направляющую, очевидно, в точке N(x, у, 0). — уравнение направляющей L в координатной плоскости Оху. Этому уравнению удовлетворяют координаты точки N. Так как точка М поверхности Р имеет ту же самую абсциссу хиту же самую ординату у, что и точка N, а переменная г в уравнение (3) не входит, то координаты точки М также удовлетворяют уравнению (3). Таким образом, координаты любой точки М(х, у, z) поверхности Р удовлетворяют уравнению (3). Обратно, если координаты какой-нибудь точки М(х, у, z) удовлетворяют уравнению (3), то эта точка расположена на прямой MN || Оz такой, что ее след на плоскости Оху, точка N(x, у, 0), лежит на линии L, а значит, точка М принадлежит цилиндрической поверхности Р. Следовательно, является уравнением цилиндрической поверхности в пространстве Oxyz, причем в этом уравнении отсутствует координата z. Пример (уравнение эллиптического цилиндра): Эллиптический цилиндр, в основании которого лежит эллипс с полуосями а и b, а осью служит ось Оz (рис. 191), на основании предыдущей теоремы имеет уравнение В частности, при а = b получаем уравнение кругового цилиндра Линию L в пространстве можно задать как пересечение двух данных поверхностей Поэтому под уравнениями линии в пространстве понимается совокупность двух уравнений: являющихся уравнениями поверхностей, определяющих данную линию. Не нужно думать, что для нахождения уравнений линий систему (4) следует «решить». Этого, вообще говоря, нельзя сделать, так как число уравнений системы (4) меньше числа неизвестных. Точный смысл, который придается равенствам (4), следующий: линии L принадлежат те и только те точки Заметим, что данную линию можно по-разному задавать как пересечение поверхностей. Поэтому линии в пространстве соответствует бесчисленное множество равносильных между собой систем уравнений. Определение: Уравнениями линии в пространстве Пример (уравнения координатных осей): Ось Ох можно, рассматривать как пересечение координатных плоскостей Оху и Oxz. Поэтому — уравнения оси Ох. Аналогично, — уравнения осей Оу и Oz соответственно. Пример: Написать уравнения окружности Г радиуса R = 1, центр которой находится в точке С(0, 0, 2) и плоскость которой параллельна координатной плоскости Оху (рис. 193). Решение: Окружность Г можно рассматривать как пересечение кругового цилиндра радиуса 1 с осью Oz и горизонтальной плоскости, расположенной выше координатной плоскости Оху на две единицы. Поэтому уравнения данной окружности есть В механике линию L часто рассматривают как след движущейся точки (рис. 194). Пусть х, у, z — текущие координаты точки М линии L. Так как с течением времени точка М перемещается и ее координаты меняются, то они являются функциями времени t. Следовательно, имеем где Исключая из уравнений (5) параметр t, мы получим два соотношения между текущими координатами х, у и z, которые представляют собой уравнения некоторых поверхностей, проходящих через данную линию. Пример: Написать уравнения винтовой линии радиуса а и шага Решение: Пусть М (х, у, z) — текущая точка винтовой линии, М’ (х, у, 0) — ее проекция на плоскость Оху. Приняв за параметр Для определения коэффициента пропорциональности b положим Исключая параметр t из первого и второго, а также из первого и третьего уравнений (6), получаем Следовательно, винтовая линия представляет собой пересечение кругового цилиндра с образующими, параллельными оси Oz, и цилиндрической поверхности с образующими, параллельными оси Оу, и имеющей своей направляющей косинусоиду, лежащую в плоскости Текущую точку ( — так называемая вектор-функция скалярного аргумента t. В механике в качестве параметра t обычно берут время. В таком случае линию (7) называют траекторией точки М(х, у, z). Множество всех точек М(х, у, г) пространства, координаты которых удовлетворяют данному уравнению (или системе уравнений), называется геометрическим образом (графиком) данного уравнения (или системы уравнений). Пример: Какой геометрический образ соответствует уравнению Решение: Из уравнения (8) получаем Пример: Какой геометрический образ соответствует паре уравнений Решение: Искомый график представляет собой пересечение плоскостей х = 2 и у = 3 и, следовательно, является прямой линией, параллельной оси Oz и имеющей след N (2, 3, 0) на координатной плоскости Оху (рис. 198). При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи Сайт пишется, поддерживается и управляется коллективом преподавателей Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC. Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг. В этой статье мы найдем ответы на вопросы о том, как создать проекцию точки на плоскость и как определить координаты этой проекции. Опираться в теоретической части будем на понятие проецирования. Дадим определения терминам, сопроводим информацию иллюстрациями. Закрепим полученные знания при решении примеров. Для удобства рассмотрения пространственных фигур используют чертежи с изображением этих фигур. Проекция фигуры на плоскость – чертеж пространственной фигуры. Очевидно, что для построения проекции существует ряд используемых правил. Проецирование – процесс построения чертежа пространственной фигуры на плоскости с использованием правил построения. Плоскость проекции — это плоскость, в которой строится изображение. Использование тех или иных правил определяет тип проецирования: центральное или параллельное. Частным случаем параллельного проецирования является перпендикулярное проецирование или ортогональное: в геометрии в основном используют именно его. По этой причине в речи само прилагательное «перпендикулярное» часто опускают: в геометрии говорят просто «проекция фигуры» и подразумевают под этим построение проекции методом перпендикулярного проецирования. В частных случаях, конечно, может быть оговорено иное. Отметим тот факт, что проекция фигуры на плоскость по сути есть проекция всех точек этой фигуры. Поэтому, чтобы иметь возможность изучать пространственную фигуру на чертеже, необходимо получить базовый навык проецировать точку на плоскость. О чем и будем говорить ниже. Напомним, что чаще всего в геометрии, говоря о проекции на плоскость, имеют в виду применение перпендикулярной проекции. Произведем построения, которые дадут нам возможность получить определение проекции точки на плоскость. Допустим, задано трехмерное пространство, а в нем — плоскость α и точка М 1 , не принадлежащая плоскости α . Начертим через заданную точку М 1 прямую а перпендикулярно заданной плоскости α . Точку пересечения прямой a и плоскости α обозначим как H 1 , она по построению будет служить основанием перпендикуляра, опущенного из точки М 1 на плоскость α . В случае, если задана точка М 2 , принадлежащая заданной плоскости α , то М 2 будет служить проекцией самой себя на плоскость α . Проекция точки на плоскость – это либо сама точка (если она принадлежит заданной плоскости), либо основание перпендикуляра, опущенного из заданной точки на заданную плоскость. Пускай в трехмерном пространстве заданы: прямоугольная система координат O x y z , плоскость α , точка М 1 ( x 1 , y 1 , z 1 ) . Необходимо найти координаты проекции точки М 1 на заданную плоскость. Решение очевидным образом следует из данного выше определения проекции точки на плоскость. Обозначим проекцию точки М 1 на плоскость α как Н 1 . Согласно определению, H 1 является точкой пересечения данной плоскости α и прямой a , проведенной через точку М 1 (перпендикулярной плоскости). Т.е. необходимые нам координаты проекции точки М 1 – это координаты точки пересечения прямой a и плоскости α . Таким образом, для нахождения координат проекции точки на плоскость необходимо: — получить уравнение плоскости α (в случае, если оно не задано). Здесь вам поможет статья о видах уравнений плоскости; — определить уравнение прямой a , проходящей через точку М 1 и перпендикулярной плоскости α (изучите тему об уравнении прямой, проходящей через заданную точку перпендикулярно к заданной плоскости); — найти координаты точки пересечения прямой a и плоскости α (статья – нахождение координат точки пересечения плоскости и прямой). Полученные данные и будут являться нужными нам координатами проекции точки М 1 на плоскость α . Рассмотрим теорию на практических примерах. Определите координаты проекции точки М 1 ( — 2 , 4 , 4 ) на плоскость 2 х – 3 y + z — 2 = 0 . Решение Как мы видим, уравнение плоскости нам задано, т.е. составлять его необходимости нет. Запишем канонические уравнения прямой a , проходящей через точку М 1 и перпендикулярной заданной плоскости. В этих целях определим координаты направляющего вектора прямой a . Поскольку прямая а перпендикулярна заданной плоскости, то направляющий вектор прямой a – это нормальный вектор плоскости 2 х – 3 y + z — 2 = 0 . Таким образом, a → = ( 2 , — 3 , 1 ) – направляющий вектор прямой a . Теперь составим канонические уравнения прямой в пространстве, проходящей через точку М 1 ( — 2 , 4 , 4 ) и имеющей направляющий вектор a → = ( 2 , — 3 , 1 ) : x + 2 2 = y — 4 — 3 = z — 4 1 Для нахождения искомых координат следующим шагом определим координаты точки пересечения прямой x + 2 2 = y — 4 — 3 = z — 4 1 и плоскости 2 х — 3 y + z — 2 = 0 . В этих целях переходим от канонических уравнений к уравнениям двух пересекающихся плоскостей: x + 2 2 = y — 4 — 3 = z — 4 1 ⇔ — 3 · ( x + 2 ) = 2 · ( y — 4 ) 1 · ( x + 2 ) = 2 · ( z — 4 ) 1 · ( y — 4 ) = — 3 · ( z + 4 ) ⇔ 3 x + 2 y — 2 = 0 x — 2 z + 10 = 0 Составим систему уравнений: 3 x + 2 y — 2 = 0 x — 2 z + 10 = 0 2 x — 3 y + z — 2 = 0 ⇔ 3 x + 2 y = 2 x — 2 z = — 10 2 x — 3 y + z = 2 И решим ее, используя метод Крамера: ∆ = 3 2 0 1 0 — 2 2 — 3 1 = — 28 ∆ x = 2 2 0 — 10 0 — 2 2 — 3 1 = 0 ⇒ x = ∆ x ∆ = 0 — 28 = 0 ∆ y = 3 2 0 1 — 10 — 2 2 2 1 = — 28 ⇒ y = ∆ y ∆ = — 28 — 28 = 1 ∆ z = 3 2 2 1 0 — 10 2 — 3 2 = — 140 ⇒ z = ∆ z ∆ = — 140 — 28 = 5 Таким образом, искомые координаты заданной точки М 1 на заданную плоскость α будут: ( 0 , 1 , 5 ) . Ответ: ( 0 , 1 , 5 ) . В прямоугольной системе координат O x y z трехмерного пространства даны точки А ( 0 , 0 , 2 ) ; В ( 2 , — 1 , 0 ) ; С ( 4 , 1 , 1 ) и М1(-1, -2, 5). Необходимо найти координаты проекции М 1 на плоскость А В С Решение В первую очередь запишем уравнение плоскости, проходящей через три заданные точки: x — 0 y — 0 z — 0 2 — 0 — 1 — 0 0 — 2 4 — 0 1 — 0 1 — 2 = 0 ⇔ x y z — 2 2 — 1 — 2 4 1 — 1 = 0 ⇔ ⇔ 3 x — 6 y + 6 z — 12 = 0 ⇔ x — 2 y + 2 z — 4 = 0 Далее рассмотрим еще один вариант решения, отличный от того, что мы использовали в первом примере. Запишем параметрические уравнения прямой a , которая будет проходить через точку М 1 перпендикулярно плоскости А В С . Плоскость х – 2 y + 2 z – 4 = 0 имеет нормальный вектор с координатами ( 1 , — 2 , 2 ) , т.е. вектор a → = ( 1 , — 2 , 2 ) – направляющий вектор прямой a . Теперь, имея координаты точки прямой М 1 и координаты направляющего вектора этой прямой, запишем параметрические уравнения прямой в пространстве: x = — 1 + λ y = — 2 — 2 · λ z = 5 + 2 · λ Затем определим координаты точки пересечения плоскости х – 2 y + 2 z – 4 = 0 и прямой x = — 1 + λ y = — 2 — 2 · λ z = 5 + 2 · λ Для этого в уравнение плоскости подставим: x = — 1 + λ , y = — 2 — 2 · λ , z = 5 + 2 · λ Теперь по параметрическим уравнениям x = — 1 + λ y = — 2 — 2 · λ z = 5 + 2 · λ найдем значения переменных x , y и z при λ = — 1 : x = — 1 + ( — 1 ) y = — 2 — 2 · ( — 1 ) z = 5 + 2 · ( — 1 ) ⇔ x = — 2 y = 0 z = 3 Таким образом, проекция точки М 1 на плоскость А В С будет иметь координаты ( — 2 , 0 , 3 ) . Ответ: ( — 2 , 0 , 3 ) . Отдельно остановимся на вопросе нахождения координат проекции точки на координатные плоскости и плоскости, которые параллельны координатным плоскостям. Пусть задана точки М 1 ( x 1 , y 1 , z 1 ) и координатные плоскости O x y , О x z и O y z . Координатами проекции этой точки на данные плоскости будут соответственно: ( x 1 , y 1 , 0 ) , ( x 1 , 0 , z 1 ) и ( 0 , y 1 , z 1 ) . Рассмотрим также плоскости, параллельные заданным координатным плоскостям: C z + D = 0 ⇔ z = — D C , B y + D = 0 ⇔ y = — D B И проекциями заданной точки М 1 на эти плоскости будут точки с координатами x 1 , y 1 , — D C , x 1 , — D B , z 1 и — D A , y 1 , z 1 . Продемонстрируем, как был получен этот результат. В качестве примера определим проекцию точки М 1 ( x 1 , y 1 , z 1 ) на плоскость A x + D = 0 . Остальные случаи – по аналогии. Заданная плоскость параллельна координатной плоскости O y z и i → = ( 1 , 0 , 0 ) является ее нормальным вектором. Этот же вектор служит направляющим вектором прямой, перпендикулярной к плоскости O y z . Тогда параметрические уравнения прямой, проведенной через точку M 1 и перпендикулярной заданной плоскости, будут иметь вид: x = x 1 + λ y = y 1 z = z 1 Найдем координаты точки пересечения этой прямой и заданной плоскости. Подставим сначала в уравнение А x + D = 0 равенства: x = x 1 + λ , y = y 1 , z = z 1 и получим: A · ( x 1 + λ ) + D = 0 ⇒ λ = — D A — x 1 Затем вычислим искомые координаты, используя параметрические уравнения прямой при λ = — D A — x 1 : x = x 1 + — D A — x 1 y = y 1 z = z 1 ⇔ x = — D A y = y 1 z = z 1 Т.е., проекцией точки М 1 ( x 1 , y 1 , z 1 ) на плоскость будет являться точка с координатами — D A , y 1 , z 1 . Необходимо определить координаты проекции точки М 1 ( — 6 , 0 , 1 2 ) на координатную плоскость O x y и на плоскость 2 y — 3 = 0 . Решение Координатной плоскости O x y будет соответствовать неполное общее уравнение плоскости z = 0 . Проекция точки М 1 на плоскость z = 0 будет иметь координаты ( — 6 , 0 , 0 ) . Уравнение плоскости 2 y — 3 = 0 возможно записать как y = 3 2 2 . Теперь просто записать координаты проекции точки M 1 ( — 6 , 0 , 1 2 ) на плоскость y = 3 2 2 : Ответ: ( — 6 , 0 , 0 ) и — 6 , 3 2 2 , 1 2 http://www.evkova.org/uravneniya-poverhnosti-i-linii-v-prostranstve http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/proektsija-tochki-na-ploskost-koordinaty-proektsii/
Решаем систему:
<(x-2)/1=(y-3)/4=(z-1)/(-3)
(x-2)/1=(y-3)/4=(z-1)/(-3) = λ ⇒
получим параметрические уравнения прямой
x= λ +2
y= 4λ +3
z=-3 λ +1
(x-2)/5=(y-3)/1=(z+1)/2=t ⇒
получим параметрические уравнения прямой
x=5t+2
y=t+3
z=2t+1Уравнения поверхности и линии в пространстве с примерами решения
Уравнения поверхности и линии в пространстве
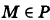
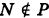
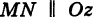


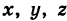
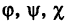
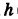
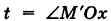
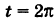
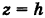
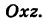
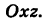
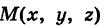
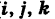
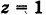
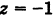
Рекомендую подробно изучить предметы: Ещё лекции с примерами решения и объяснением: Проекция точки на плоскость, координаты проекции точки на плоскость
Проецирование, виды проецирования
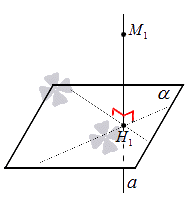
Проекция точки на плоскость
Нахождение координат проекции точки на плоскость, примеры