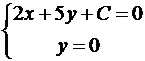Составить уравнение прямой a4n параллельной прямой a1a2

Уравнение прямой, проходящей через две точки онлайн

С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через две точки. Дается подробное решение с пояснениями. Для построения уравнения прямой задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точек в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Уравнение прямой, проходящей через две точки − примеры и решения

Пример 1. Построить прямую, проходящую через точки A(2, 1, 1), B(3, 1, -2).

(1)

Подставив координаты точек A и B в уравнение (1), получим:

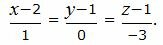(Здесь 0 в знаменателе не означает деление на 0).

Составим параметрическое уравнение прямой:

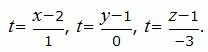Выразим переменные x, y, z через параметр t :

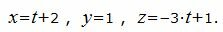Каноническое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2) имеет следующий вид:

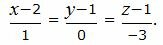Параметрическое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2) имеет следующий вид:

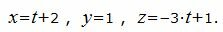Пример 2. Построить прямую, проходящую через точки A(1, 1/5, 1) и B(−2, 1/2, −2).

(2)

Подставив координаты точек A и B в уравнение (2), получим:

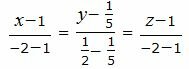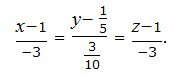Составим параметрическое уравнение прямой:

Выразим переменные x, y, z через параметр t :

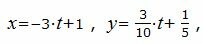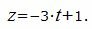Каноническое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:

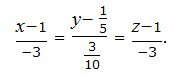Параметрическое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:

Уравнение параллельной прямой

Альтернативная формула:
Прямая, проходящая через точку M₁(x₁; y₁) и параллельная прямой Ax+By+C=0 , представляется уравнением

назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения параллельной прямой (см. также как составить уравнение перпендикулярной прямой).

Пример №2 . Написать уравнение прямой, параллельной прямой 2x + 5y = 0 и образующей вместе с осями координат треугольник, площадь которого равна 5.
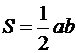
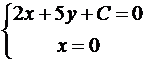
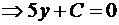
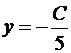
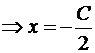
Решение. Так как прямые параллельны, то уравнение искомой прямой 2x + 5y + C = 0. Площадь прямоугольного треугольника , где a и b его катеты. Найдем точки пересечения искомой прямой с осями координат:
;
.
Итак, A(-C/2,0), B(0,-C/5). Подставим в формулу для площади: 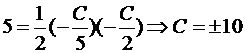. Получаем два решения: 2x + 5y + 10 = 0 и 2x + 5y – 10 = 0 .

Пример №3 . Составить уравнение прямой, проходящей через точку (-2; 5) и параллельной прямой 5x-7y-4=0 .
Решение. Данную прямую можно представить уравнением y = 5 /₇x – 4 /₇ (здесь a = 5 /₇). Уравнение искомой прямой есть y – 5 = 5 / 7(x – (-2)), т.е. 7(y-5)=5(x+2) или 5x-7y+45=0 .

Пример №4 . Решив пример 3 (A=5, B=-7) по формуле (2), найдем 5(x+2)-7(y-5)=0.

Пример №5 . Составить уравнение прямой, проходящей через точку (-2;5) и параллельной прямой 7x+10=0.
Решение. Здесь A=7, B=0. Формула (2) дает 7(x+2)=0, т.е. x+2=0. Формула (1) неприменима, так как данное уравнение нельзя разрешить относительно y (данная прямая параллельна оси ординат).

Составить уравнение прямой a4n параллельной прямой a1a2

Даны четыре точки A1( 5; 3; 7), A2 (-2; 3; 7), A3(4; 2; 10), A4(1; 2; 7).

а) плоскости А1А2А3;

Находим векторы А1А2 и А1А3.

А1А2 = (-2-5; 3-3; 7-7) = (-7; 0; 0).

А1А3 = (4-5; 2-3; 10-7) = (-1; -1; 3).

Нормальный вектор плоскости А1А2А3 находим из векторного произведения векторов А1А2 и А1А3.

-1 -1 3| -1 -1 = 0i + 0j + 7k + 21j + 0i + 0k =

Нормальный вектор плоскости А1А2А3 равен (0; 21; 7).

Подставляем найденные координаты нормального вектора в уравнение плоскости:

21y+7z−112=0 или после сокращения на 7:

Уравнение А1А2А3: 3y + z — 16.

Из этого уравнения можно принять нормальный вектор плоскости А1А2А3 равным (0; 3; 1).

Направляющий вектор найден выше: А1А2 = (-7; 0; 0).

Уравнение А1А2: (x — 5)/(-7) = (y — 3)/0 = (z — 7)/0.

Это уравнение прямой, параллельной оси абсцисс.

в) прямой А4М перпендикулярной к плоскости А1А2А3;

Направляющим вектором прямой А4М является нормальный вектор плоскости А1А2А3, найденный ранее и равный (0; 3; 1).

Уравнение А4М: (x — 1)/0 = (y — 2)/3 = (z — 7)/1.

г) прямой А3 N параллельной прямой А1А2.

У этой прямой направляющий вектор равен вектору А1А2,

Уравнение А3N: (x — 4)/(-7) = (y — 2)/0 = (z — 10)/0.

Это уравнение прямой, параллельной оси абсцисс.

д) плоскости проходящей через точку А4 перпендикулярно к прямой А1 А2.

У этой плоскости нормальный вектор совпадает с вектором А1А2.

после сокращения на -7 получаем

x – 1 = 0.

e) синус угла между прямой A1A4 и плоскостью A1A2A3.

= 21 = 0,23009

Угол равен 0,23217 радиан или 13,3023 градуса.

ж) косинус угла между координатной плоскостью Oxy и плоскостью A1A2A3.

Координатная плоскость Oxy имеет уравнение z = 0.

Уравнение плоскости А1А2А3: 3y + z — 16.

Вычислим угол между плоскостями

z = 0 и 3y + z – 16.

cos α = |A1·A2 + B1·B2 + C1·C2|/(√(A1² + B1² + C1²)* √(A2² + B2² + C2²)).

cos α = |0·0 + 0·3 + 1·1|/(√(0² + 0² + 1²)* √(0² + 3² + 1²)) =

= |0 + 0 + 1|/(√(0 + 0 + 1)* √(0 + 9 + 1)) =

= 1/√1* √10 = 1/√10 = √10/10 ≈ 0,3162.