Составить уравнение прямой перпендикулярной вектору онлайн

Уравнение перпендикулярной прямой

Альтернативная формула
Прямая, проходящая через точку M₁(x₁; y₁) и перпендикулярная прямой Ax+By+C=0 , представляется уравнением

назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения перпендикулярной прямой (см. также как составить уравнение параллельной прямой).

Пример №1 . Составить уравнение прямой, проходящей через точку (2; -1) и перпендикулярной 4x-9y=3 .
Решение. Данную прямую можно представить уравнением y = 4 /₉x – 1 /₃ (a = 4 /₉). Уравнение искомой прямой есть y+1 = -9/4(x-2) , т.е. 9x+4y-14=0 .

Пример №2 . Решая пример 1 (A=4, B=-9) по формуле (2), найдем 4(y+1)+9(x-2)=0 , т.е. 9x+4y-14=0 .

Пример №3 . Составить уравнение прямой, проходящей через точку (-3, -2) перпендикулярно прямой 2y+1=0 .
Решение. Здесь A=0, B=2. Формула (2) дает -2(x+3)=0, т.е. x+3=0 . Формула (1) неприменима, так как a=0 .

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости онлайн

С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через данную точку и перпендикуляной данной плоскости. Дается подробное решение с пояснениями. Для построения уравнения прямой введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости

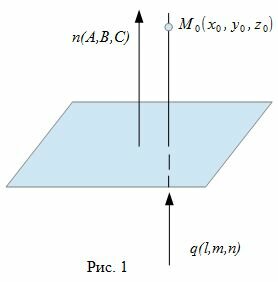
Наша цель построить уравнение прямой, проходящей через данную точку M₀ и перпендикулярной к данной плоскости Ax+By+Cz+D=0.

Общее уравнение плоскости имеет вид:

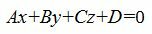(1)

где n(A,B,C)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

(2)

Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .

Таким образом, уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и ортогональный плоскости (1) имеет следующий вид:

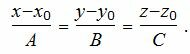(3)

Пример 1. Построить прямую, проходящую через точку M₀(5, -4, 4) и перпендикулярной плоскости

Общее уравнение плоскости имеет вид (1), где :

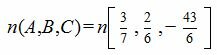(4)

Подставляя координаты точки M₀(5, -4, 4) и координаты нормального вектора плоскости (4) в (3), получим:

Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору

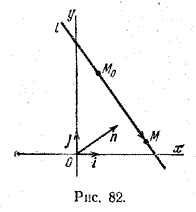
Пусть дана некоторая точка М₀ и вектор n. Проведем через точку М₀ прямую l перпендикулярно вектору n (рис. 82).

Пусть M — произвольная точка. Точка M лежит на прямой l в том и только в том случае, когда вектор \(\overrightarrowM>\) перпендикулярен вектору n, а для этого необходимо и достаточно, чтобы скалярное произведение векторов n и \(\overrightarrowM>\) равнялось нулю:

Чтобы выразить последнее равенство в координатах, введем прямоугольную декартову систему координат. Пусть точки M₀ и M имеют координаты (x₀ ; у₀ ) и (x; у).

Тогда \(\overrightarrowM>\) = (x — x₀; у — у₀). Обозначим координаты нормального вектора n через (А; В). Теперь равенство (1) можно записать так:

Уравнение (2) есть уравнение прямой l, проходящей через данную точку М₀ (x₀; у₀) перпендикулярно данному вектору n = (А; В).

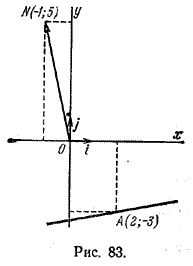
Задача 1. Составить уравнение прямой, проходящей через точку А (2; -3) перпендикулярно вектору n = (-1;5) (рис.83).

Пользуясь формулой (2), находим уравнение данной прямой:

— 1 • (x-2) + 5 • (у + 3) = 0

или, окончательно, x — 5у — 17 = 0.

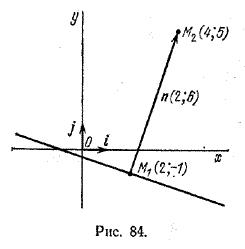
Задача 2. Даны точки M₁(2; -1) и M₂(4; 5). Написать уравнение прямой, проходящей через точку М₁ перпендикулярно вектору \(\overrightarrowM_<2>>\).

Нормальный вектор искомой прямой n = \(\overrightarrowM_<2>>\) имеет координаты (2; 6) (рис. 84).

Следовательно, по формуле (2) получим уравнение

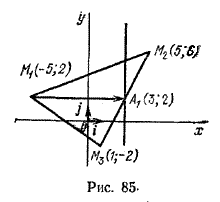
Задача 3. В треугольнике с вершинами в точках M₁(-5; 2), M₂(5; 6) и M₃(1; -2) проведена медиана M₁А₁. Требуется составить уравнение прямой, проходящей через точку А₁ перпендикулярно медиане M₁A₁ (рис. 85).

За нормальный вектор искомой прямой можно принять вектор n = \(\overrightarrowA_<1>>\). Определим его координаты. Точка A₁ — середина отрезка M₂M₃, поэтому, если (x₁; y₁) — ее координаты, то \( x_1 = \frac<5+1><2>=3, \;\;а \;\; y_1=\frac<6-2><2>=2 \).

Тогда нормальный вектор n = \(\overrightarrowA_<1>>\) имеет координаты (8; 0). Следовательно, искомое уравнение прямой имеет вид

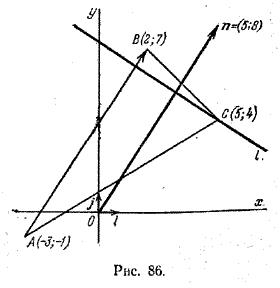
Задача 4. Дан треугольник с вершинами в точках А(-3; -1), В(2; 7) и С(5; 4). Требуется составить уравнение прямой, проходящей через вершину С перпендикулярно стороне AB (рис. 86).

За нормальный вектор искомой прямой можно взять вектор n = \(\overrightarrow\).

Так как n = (2-(-3); 7 — (-1)) = (5; 8), то, подставляя координаты точки С и координаты вектора n в формулу (2), получим

или, окончательно, 5х + 8у — 57 = 0.