Составить уравнение прямой проходящей через середину отрезка ав

Составить уравнение прямой проходящей через середину отрезка АВ, параллельно прямой y = 2x + 5 , если А (2, — 1) и В (0, 7)?

Геометрия | 5 — 9 классы

Составить уравнение прямой проходящей через середину отрезка АВ, параллельно прямой y = 2x + 5 , если А (2, — 1) и В (0, 7).

Прямая — график линейной функции, то есть y = kx + b.

Так как искомаяпрямая проходит параллельно прямой y = 2x + 5, то их угловые коэфициенты равны.

Середина отрезка AB — точка O.

Найдем ее координаты :

x = (xA + xB) / 2 = (2 + 0) / 2 = 1

y = (yA + yB) / 2 = ( — 1 + 7) / 2 = 3

Найдем b, для этого подставим координаты точки O :

значит искомое уравнение прямой — y = 2x + 1.

Отрезки АВ и CD пересекаются в их общей середине?

Отрезки АВ и CD пересекаются в их общей середине.

Докажите, что прямые АС и BD параллельны.

) Вершины В и С треугольника АВС лежат в плоскости \ beta ?

) Вершины В и С треугольника АВС лежат в плоскости \ beta .

Вершина А ей не принадлежит.

Докажите, что прямая, проходящая через середины отрезков АВ и АС, параллельна плоскости \ beta .

1) Вершины В и С треугольника АВС лежат в плоскости ?

1) Вершины В и С треугольника АВС лежат в плоскости .

Вершина А ей не принадлежит.

Докажите, что прямая, проходящая через середины отрезков АВ и АС, параллельна плоскости .

Концы отрезка АВ лежат на параллельных прямых a и b?

Концы отрезка АВ лежат на параллельных прямых a и b.

Прямая, проходящая через середину О этого отрезка , пересекает прямые a и b в точках С и D.

Докажите что СО = ОD.

Отрезки АВ и СD пересекаются в их общей середине?

Отрезки АВ и СD пересекаются в их общей середине.

Докажите, что прямые AC и BD параллельны.

Отрезки АВ и CD пересекаются в точке О, являющейся их серединой?

Отрезки АВ и CD пересекаются в точке О, являющейся их серединой.

Докажите параллельность прямых АС и ВD.

Докажите, что середина отрезка прямой, заключенного между двумя параллельными прямыми, является серединой отрезков прямых, проходящих через эту точку и заключенных между теми же параллельными прямыми?

Докажите, что середина отрезка прямой, заключенного между двумя параллельными прямыми, является серединой отрезков прямых, проходящих через эту точку и заключенных между теми же параллельными прямыми.

Перпендикулярные отрезки KN и PM пересекаются в их общей середине?

Перпендикулярные отрезки KN и PM пересекаются в их общей середине.

Начертите прямую, проходящую через точку К, параллельную прямой, содержащей отрезок PM.

⦁Отрезки АС и BD пересекаются в их общей середине точке О?

⦁Отрезки АС и BD пересекаются в их общей середине точке О.

Докажите, что прямые АВ и CD параллельны.

Постройте прямую, проходящую через середину О отрезка АВ и перпендикулярную этому отрезку?

Постройте прямую, проходящую через середину О отрезка АВ и перпендикулярную этому отрезку.

На этой странице сайта, в категории Геометрия размещен ответ на вопрос Составить уравнение прямой проходящей через середину отрезка АВ, параллельно прямой y = 2x + 5 , если А (2, — 1) и В (0, 7)?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Если ребро куба равно х, то диагональ куба равна х√3 . Так как в этой задаче ребро куба равно 1, то диагональ куба равна 1 * √3 = √3.

Ответ : a = 2√6Объяснение : b = 6 — боковая сторона равнобедренного треугольникаcos α = 2 / 3 (α — угол между боковыми сторонами)а — ? — основание треугольника — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — Применим ..

Ответ : √24Объяснение : Пусть в равнобедренном треугольнике ΔАВС боковые стороны АВ = ВС = 6 и cos∠В = 2 / 3 (см. Рисунок). Применяя теорему косинусов определим основание АС : АС² = АВ² + BС² — 2 · АВ · BС · cos∠В = 6² + 6² — 2 · 6 · 6 · 2 / 3 = 36..

Даны точки A(2,-3) и B(3,-5).Через середину отрезка AB провести прямую, перпендикулярную отрезку AB

Тему в универе ещё не проходили, попросила помочь знакомая. Отказывать некрасиво, а как решить не знаю. Очень прошу помочь.

Вектор АВ = (3-2; -5+3) = (1; -2). Этот вектор является вектором нормали прямой. Пусть срединой отрезка АВ является точка О. Ее координаты О (2,5; -4). Уравнение прямой по точке и нормали: 1*(х — 2,5) — 2*(у + 4) =0. Отсюда уравнение прямой в общем виде: х — 2у — 10,5=0

Уравнение прямой в отрезках: описание, примеры, решение задач

Продолжаем изучение раздела «Уравнение прямой на плоскости» и в этой статье разберем тему «Уравнение прямой в отрезках». Последовательно рассмотрим вид уравнения прямой в отрезках, построение прямой линии, которая задается этим уравнением, переход от общего уравнения прямой к уравнению прямой в отрезках. Все это будет сопровождаться примерами и разбором решения задач.

Уравнение прямой в отрезках – описание и примеры

Пусть на плоскости расположена прямоугольная система координат O x y .

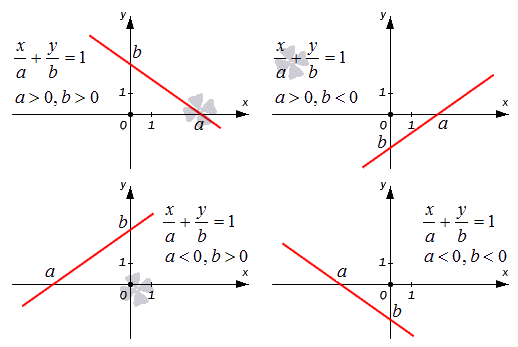
Прямая линия на плоскости в декартовой системе координат O x y задается уравнением вида x a + y b = 1 , где a и b – это некоторые действительные числа, отличные от нуля, величины которых равны длинам отрезков, отсекаемых прямой линией на осях O x и O y . Длины отрезков считаются от начала координат.

Как мы знаем, координаты любой из точек, принадлежащих прямой линии, заданной уравнением прямой, удовлетворяют уравнению этой прямой. Точки a , 0 и 0 , b принадлежат данной прямой линии, так как a a + 0 b = 1 ⇔ 1 ≡ 1 и 0 a + b b = 1 ⇔ 1 ≡ 1 . Точки a , 0 и b , 0 расположены на осях координат O x и O y и удалены от начала координат на a и b единиц. Направление, в котором нужно откладывать длину отрезка, определяется знаком, который стоит перед числами a и b . Знак « — » обозначает, что длину отрезка необходимо откладывать в отрицательном направлении координатной оси.

Поясним все вышесказанное, расположив прямые относительно фиксированной декартовой системы координат O x y на схематическом чертеже. Уравнение прямой в отрезках x a + y b = 1 применяется для построения прямой линии в декартовой системе координат O x y . Для этого нам необходимо отметить на осях точки a , 0 и b , 0 , а затем соединить эти точки линией при помощи линейки.

На чертеже показаны случаи, когда числа a и b имеют различные знаки, и, следовательно, длины отрезков откладываются в разных направлениях координатных осей.

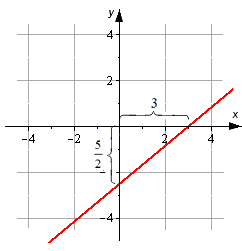
Прямая линия задана уравнением прямой в отрезках вида x 3 + y — 5 2 = 1 . Необходимо построить эту прямую на плоскости в декартовой системе координат O x y .

Решение

Используя уравнение прямой в отрезках, определим точки, через которые проходит прямая линия. Это 3 , 0 , 0 , — 5 2 . Отметим их и проведем линию.

Приведение общего уравнения прямой к уравнению прямой в отрезках

Переход от заданного уравнения прямой к уравнению прямой в отрезках облегчает нам решение различных задач. Имея полное общее уравнение прямой, мы можем получить уравнение прямой в отрезках.

Полное общее уравнение прямой линии на плоскости имеет вид A x + B y + C = 0 , где А , В и C не равны нулю. Мы переносим число C в правую часть равенства, делим обе части полученного равенства на – С . При этом, коэффициенты при x и y мы отправляем в знаменатели:

A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1

Для осуществления последнего перехода мы воспользовались равенством p q = 1 q p , p ≠ 0 , q ≠ 0 .

В результате, мы осуществили переход от общего уравнения прямой A x + B y + C = 0 к уравнению прямой в отрезках x a + y b = 1 , где a = — C A , b = — C B .

Разберем следующий пример.

Осуществим переход к уравнению прямой в отрезках, имея общее уравнение прямой x — 7 y + 1 2 = 0 .

Решение

Переносим одну вторую в правую часть равенства x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .

Делим обе части равенства на — 1 2 : x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .

Преобразуем полученное равенство к нужному виду: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .

Мы получили уравнение прямой в отрезках.

Ответ: x — 1 2 + y 1 14 = 1

В тех случаях, когда прямая линия задана каноническим или параметрическим уравнением прямой на плоскости, то сначала мы переходим к общему уравнению прямой, а затем уже к уравнению прямой в отрезках.

Перейти от уравнения прямой в отрезках и общему уравнению прямой осуществляется просто: мы переносим единицу из правой части уравнения прямой в отрезках вида x a + y b = 1 в левую часть с противоположным знаком, выделяем коэффициенты перед неизвестными x и y .

x a + y b = 1 ⇔ x a + y b — 1 = 0 ⇔ 1 a · x + 1 b · y — 1 = 0

Получаем общее уравнение прямой, от которого можно перейти к любому другому виду уравнения прямой на плоскости. Процесс перехода мы подробно разобрали в теме «Приведение общего уравнения прямой к другим видам уравнения прямой».

Уравнение прямой в отрезках имеет вид x 2 3 + y — 12 = 1 . Необходимо написать общее уравнение прямой на плоскости.

Решение

Действует по заранее описанному алгоритму:

x 2 3 + y — 12 = 1 ⇔ 1 2 3 · x + 1 — 12 · y — 1 = 0 ⇔ ⇔ 3 2 · x — 1 12 · y — 1 = 0

Ответ: 3 2 · x — 1 12 · y — 1 = 0