Составить уравнение прямой содержащей биссектрису

Задача 27274 4.2.42. Найти уравнение прямой.

Условие

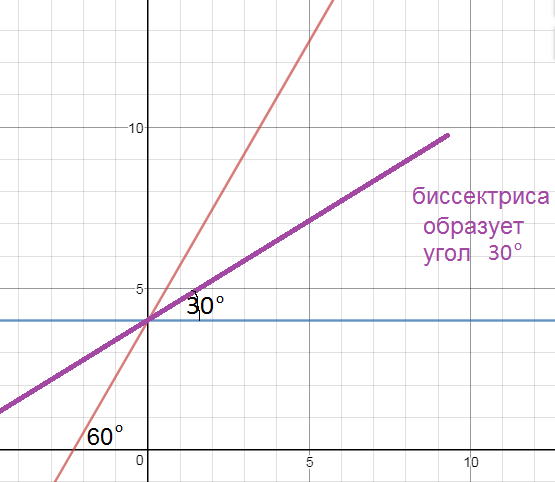
4.2.42. Найти уравнение прямой, содержащей биссектрису острого угла, образованного прямыми y=sqrt(3)x+4 и y=4

Решение

Геометрический смысл углового коэффициента k в уравнении прямой у=kx+b
k=tg альфа ,
альфа — угол который образует прямая у =kx+b с положительным направлением оси Ох.

В уравнении прямой y=√3x+4
k=sqrt(3)
Значит,
tg альфа = sqrt(3)
альфа =60^(o)

y=4 параллельна оси Ох.
Значит угол между прямыми y=√3x+4 и y=4 равен 60^(o)

Биссектриса делит угол в 60^(o) пополам и образует с осью Ох и прямой у=4 угол 30 градусов

у=(sqrt(3)/3)x + b — уравнение прямых, образующих с осью Ох угол в 30 градусов. Чтобы выделить среди них биссектрису острого угла, образованного прямыми y=√3x+4 и y=4, подставим координаты их точки пересечения и найдем b

О т в е т. у=(sqrt(3)/3)х+4

Составить уравнение прямой содержащей биссектрису

Найти уравнение биссектрис углов между прямыми 12x + 9y — 17 = 0 и 3x + 4y + 11 = 0.

Из элементарной геометрии известно, что биссектриса угла между двумя прямыми есть геометрическое место точек, равноудаленных от сторон угла. Обратимся к рисунку

Отклонения и точки A биссектрисы от сторон угла CDE имеют знак плюс, так как точка A и начало координат лежат по разные стороны как от первой, так и от второй прямой, т. е. . Возьмем точку B на биссектрисе смежного угла CDF. Точка B и начало координат лежат по разные стороны от прямой EF, поэтому отклонение имеет знак плюс ( > 0). Отклонение точки B от прямой CL имеет знак минус, так как точка B и начало координат лежат с одной и той же стороны от прямой CL, т. е. C₁ = 0 и A₂x + B₂y + C₂ = 0.

Прямая на плоскости. Примеры решений

Решение проводим с помощью калькулятора.
Даны координаты треугольника: A(2,1), B(1,-2), C(-1,0).
1) Координаты векторов
Координаты векторов находим по формуле:
X = x_j — x_i; Y = y_j — y_i
здесь X,Y координаты вектора; x_i, y_i — координаты точки А_i; x_j, y_j — координаты точки А_j
Например, для вектора AB
X = x₂ — x₁; Y = y₂ — y₁
X = 1-2 = -1; Y = -2-1 = -3
AB(-1;-3)
AC(-3;-1)
BC(-2;2)
2) Модули векторов
Длина вектора a(X;Y) выражается через его координаты формулой:




3) Угол между прямыми
Угол между векторами a₁(X₁;Y₁), a₂(X₂;Y₂) можно найти по формуле:

где a₁a₂ = X₁X₂ + Y₁Y₂
Найдем угол между сторонами AB и AC

γ = arccos(0.6) = 53.13 0
4) Проекция вектора
Проекцию вектора b на вектор a можно найти по формуле:

Найдем проекцию вектора AB на вектор AC

5) Площадь треугольника
Пусть точки A₁(x₁; y₁), A₂(x₂; y₂), A₃(x₃; y₃) — вершины треугольника, тогда его площадь выражается формулой:

В правой части стоит определитель второго порядка. Площадь треугольника всегда положительна.
Решение. Принимая A за первую вершину, находим:

Пример. Даны координаты вершин треугольника АВС: А(–3; –1), В(4; 6), С(8; –2).
Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.

Задание. Даны координаты вершин треугольника ABC: A(7;4), B(-9;-8), C(-2;16). Требуется:

1. составить уравнение медианы, проведенной из вершины B, и вычислить ее длину.
2. составить уравнение высоты, проведенной из вершины A, и вычислить ее длину.
3. найти косинус внутреннего угла B треугольника ABC.

Сделать чертеж.

Пример №3. Даны вершины A(1;1), B(7;4), C(4;5) треугольника. Найти: 1) длину стороны AB ; 2) внутренний угол A в радианах с точностью до 0,001. Сделать чертеж.
Скачать

Пример №4. Даны вершины A(1;1), B(7;4), C(4;5) треугольника. Найти: 1) уравнение высоты, проведенной через вершину C ; 2) уравнение медианы, проведенной через вершину C ; 3) точку пересечения высот треугольника; 4) длину высоты, опущенной из вершины C. Сделать чертеж.
Скачать

Пример №5. Даны вершины треугольника ABC: A(-5;0), B(7;-9), C(11;13). Определите: 1) длину стороны AB ; 2) уравнение сторон AB и AC и их угловые коэффициенты; 3) площадь треугольника.

• Решение
• Видео решение

Задание. Найти острый угол между прямыми x + y -5 = 0 и x + 4y — 8 = 0 .
Рекомендации к решению. Задача решается посредством сервиса Угол между двумя прямыми.
Ответ: 30.96 o

Пример №1. Даны координаты точек А1(1;0;2), A2(2;1;1), А3(-1;2;0), A4(-2;-1;-1). Найти длину ребра А1А2. Составить уравнение ребра А1А4 и грани А1А2А3. Составить уравнение высоты опущенной из точки А4 на плоскость А1А2А3. Найти площадь треугольника А1A2A3. Найти объем треугольной пирамиды А1A2А3A4.

• Решение
• Видео решение

Задание. По координатам вершин пирамиды А1,А2,А3,А4 найти: 1) длины ребер А1А2 и А1А3; 2) угол между ребрами А1А2 и А1А3; 3) площадь грани А1А2А3;4) объем пирамиды А1А2А3А4
A₁(3;5;4,0,0), A₂(8;7;4,0,0), A₃(5;10;4,0,0), A₄(4;7;9,0,0):Пример №10

Пример. В декартовой прямоугольной системе координат даны вершины пирамиды A, B, C, D. Найдите длину ребра AB, косинус угла между векторами, уравнение ребра, уравнение грани, уравнение высоты.
Решение

Пример. Даны вершины треугольника А(1, –1, -3), В(2, 0, -10), С(3, 0, -2).
а) Найти уравнение биссектрисы и высоты данного треугольника, проведенных из вершины A .
б) Найти уравнения всех его медиан и координаты точки их пересечения.
см. также Как найти периметр треугольника