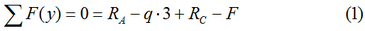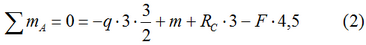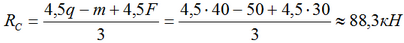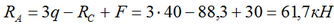Составить уравнение равновесия двухопорной балки

Двухопорная балка

Содержание:

Исходные данные:

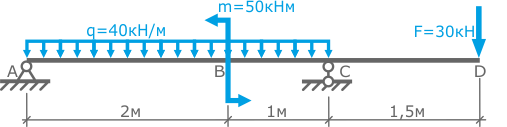
Заданная расчетная схема:

Пример решения задачи

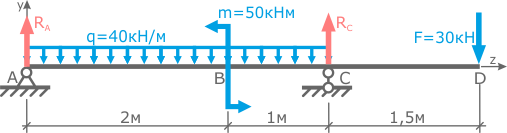
1. Определяем опорные реакции (рис.2.1).

Рассматриваемая двухопорная балка является статически определимой. Это означает, что для определения неизвестных опорных реакций и в наложенным внешних связях (двухсвязный шарнир и односвязный шарнир достаточно только уравнений равновесия (независимыми уравнениями для плоской системы являются

Наиболее рациональной является следующая схема определения опорных реакций в двухопорных балках. Из уравнения определяется горизонтальная реакция Как правило, в балках она равна нулю (при отсутствии продольной внешней нагрузки, которая не является характерной нагрузкой при изгибе).

• Вертикальные опорные реакции на каждой опоре определяются из суммы моментов всей внешней нагрузки относительно противоположной опоры (соответственно

Поскольку в этих уравнениях реакции будут единственными неизвестными, при таком подходе каждая из этих реакций может быть получена в виде дроби, в знаменателе которой будет расстояние между опорами, а в числителе — сумма моментов всей внешней активной нагрузки относительно противоположной опоры, взятых со знаками, противоположными знаку выбранного

направления искомой реакции. Уравнения являются зависимыми, то есть являются по сути одним и тем же уравнением. Поэтому всегда необходимо проверять правильность определения опорных реакций, используя для этого оставшееся независимое уравнение равновесия

Возможно вам будут полезны данные страницы:

Таким образом, рациональный алгоритм определения опорных реакций в двухопорных балках имеет следующий вид:

1.1. Определяем опорную реакцию

1.2. Определяем опорную реакцию

1.3. Проверяем правильность определения опорных реакций:

Знак «-» у полученных опорных реакций показывает, что они направлены в сторону, противоположную выбранной (не вверх, а вниз).

Составляем уравнения изменения поперечных сил и изгибающих моментов для каждого участка балки.

Поперечная сила и изгибающий момент являются внутренними усилиями (внутренними силовыми факторами) и, как и при других видах напряженного состояния, определяются при помощи метода сечений. Суть метода заключается в том, что балка мысленно рассекается в заданном сечении на две части, отбрасывается одна из частей (как правило, большая), для восстановления равновесия действие отброшенной части на оставшуюся заменяется (компенсируется) внутренними усилиями, которые определяются из уравнений равновесия оставшейся (рассматриваемой) части балки.

• Однако, в таком общем виде внутренние усилия при изгибе обычно не определяются. Как правило, для составления уравнений достаточно математических определений поперечной силы и изгибающего момента и правила знаков для учета внешней нагрузки.

Математические определений внутренних усилий при изгибе:

Поперечная сила в заданном поперечном сечении балки равна сумме проекций всей внешней нагрузки, действующей с одной стороны от сечения (или в рассматриваемой части балки), на вертикальную ось

Изгибающий момент в заданном поперечном сечении равен сумме моментов относительно оси от всей внешней нагрузки, действующей с одной стороны от сечения (или в рассматриваемой части балки).

Правило знаков необходимо использовать для учета направлений действия внешней нагрузки в математических определениях внутренних усилий. На рис.2.2 показано правило знаков для поперечных сил и изгибающих моментов при изгибе балок. На схемах указаны направления действия внешней нагрузки, вызывающей положительные значения внутренних усилий в указанном поперечном сечении рассматриваемой левой (правило знаков слева) или правой (правило знаков справа) части балки.

Систематизируя правило знаков слева и справа, можно сформулировать следующие общие определения правила знаков при изгибе:

• Правило знаков для поперечной силы — если внешняя нагрузка стремится повернуть рассматриваемую часть балки по ходу часовой стрелки, то она вызывает в заданном поперечном сечении положительную поперечную силу.
• Правило знаков для изгибающего момента — если внешняя нагрузка стремится поднять рассматриваемую часть балки вверх, то она вызывает в заданном поперечном сечении положительный изгибающийся момент.

Составление уравнений изменения внутренних усилий при изгибе для каждого участка сопровождается такими обязательными комментариями:

• а) необходимо обязательно указывать номер участка на расчетной схеме, во всех уравнениях и при вычислении значений внутренних усилий в характерных точках участка;
• б) так как при изгибе поперечное сечение проводится в произвольной, но фиксированной точке участка, необходимо показывать привязку этой точки к выбранному началу координат (как правило, в крайней левой или крайней правой точке балки) при помощи переменной координаты
• в) необходимо указывать интервал изменения переменной в пределах каждого участка и указывать, какое правило знаков (слева или справа) используется при составлении уравнений.

Конечной целью определения внутренних усилий является построение эпюр. Для этого необходимо знать значение внутренних усилий в характерных точках участков. Такими точками являются поперечные сечения в начале и конце участка, а также сечения с возможными экстремальными значениями внутренних усилий. Экстремальные (отличные от соседних) значения могут возникать в случае, если уравнение изменения внутренних усилий имеет форму полинома второго и выше порядка.

Для заданной балки уравнения изменения внутренних усилий и их значения в характерных точках для трех участков имеют вид (рис.2.3):

Уравнение изменения изгибающего момента для первого участка имеет форму полинома второй степени и, следовательно, изгибающий момент в пределах первого участка может иметь экстремум. Координату экстремума можно определить, приравняв первую производную функции к нулю. Для этого удобно использовать первую теорему Журавского (2.1). Определяем координату экстремума

Определяем значение экстремального изгибающего момента

Уравнение изменения изгибающего момента для второго участка также имеет форму полинома второй степени. Однако, поперечная сила в пределах участка не меняет свой знак, и, следовательно, ввиду линейности функции в пределах участка не может быть равной нулю. Поэтому экстремального значения изгибающего момента на втором участке не будет.

Уравнение изменения изгибающего момента для третьего участка имеет форму полинома второй степени, а поперечная сила пределах участка меняет свой знак. Следовательно, нужно определять положение экстремума

Определяем значение экстремального изгибающего момента

3. Строим эпюры поперечных сил и изгибающих моментов

Эпюрой в сопротивлении материалов называется график, отражающий характер изменения какого-либо параметра вдоль оси одноосного элемента. Эпюры строятся для каждого участка в отдельности. В пределах участка все расчетные параметры изменяются по определенному закону в виде неразрывной функции. Для построения эпюры на каждом участке необходимо знать характер изменения заданного параметра в пределах участка (его математическое выражение) и значения в нескольких характерных точках (как правило, в начале и конце участка и, если необходимо, в точках экстремальных значений параметра).

Согласно полученных ранее уравнений, графиком эпюры поперечных сил на всех участках будет прямая наклонная линия, а графиком эпюры изгибающих моментов — квадратная парабола.

При построении эпюр необходимо соблюдать следующие правила:

а) название эпюры обычно приводится справа или сверху от нее, при этом, если все значения на эпюре поперечных сил приведены в а на эпюре изгибающих моментов — в то размерность не указывается;

б) построение эпюры не требует точного соблюдения масштаба, однако примерная видимая пропорциональность между значениями параметров должна соблюдаться;

в) знаки параметров указываются или в «теле эпюры», или слева от нее;

г) «тело эпюры» заштриховывается поперечной (перпендикулярной по отношению к продольной оси одноосного элемента) штриховкой, при этом величина каждого штриха характеризует значение расчетного параметра в соответствующем сечении.

Под «телом эпюры» понимаются плоские фигуры, ограниченные продольной осью одноосного элемента и графиком уравнений изменения расчетных параметров.

Эпюра поперечных сил для заданной двухопорной балки приведена на рис.2.3г, изгибающих моментов — на рис.2.3г).

Если положительные значения изгибающих моментов на эпюре откладываются вверх, такая эпюра называется «эпюрой по сжатым волокнам». В такой эпюре «тело» эпюры располагается с той стороны балки (вверху или внизу), волокна которой сжаты. Такая эпюра характерна для машиностроителей. Если положительные значения откладываются вниз — эпюра называется «по растянутым волокнам». Она характерна для строителей. а) скачки (резкие изменения значений параметра в одном и том же поперечном сечении) на эпюре поперечных сил должны соответствовать по координате, величине и знаку внешним сосредоточенным силам;

б) скачки на эпюре изгибающих моментов должны соответствовать по координате, величине и знаку внешним сосредоточенным моментам;

в) в соответствии с первой теоремой Журавского (2.1) в поперечных сечениях, в которых поперечная сила равна нулю, изгибающий момент принимает экстремальные значения;

г) в соответствии со второй теоремой Журавского (2.2) при графиком эпюры поперечных сил при движении слева направо будет восходящая прямая линия, справа налево — нисходящая.

д) в соответствии с (2.3) при в поперечных сечениях, в которых поперечная сила равна нулю, экстремумами на эпюре изгибающих моментов будут минимумы, а при — максимумы.

Для построенных эпюр (рис.2.3) все указанные признаки выполняются.

Подбираем поперечное сечение балки из условия прочности в форме двутавра, прямоугольника круга и из двух швеллеров

Для заданной балки максимальный изгибающий момент в опасном сечении равен (рис.2.3г)).

Согласно (2.6) минимально допустимый осевой момент сопротивления поперечного сечения балки определяется зависимостью

Двутавровое поперечное сечение.

Двутавр является стандартным прокатным профилем, все геометрические характеристики которого приводятся в справочных таблицах. Согласно (2.8) минимальное значение момента сопротивления будет равно:

Из справочных таблиц (ГОСТ 8239-86) выбираем двутавр с ближайшим большим значением момента сопротивления. Это двутавр № 36, для которого

Поперечное сечение в форме прямоугольника.

Прямоугольник является сечением простой геометрической формы, для которого все геометрические характеристики определяются по известным аналитическим зависимостям. Осевой момент сопротивления прямоугольного сечения с соотношением высоты и основания равен

Тогда, согласно (2.6), минимальная ширина прямоугольного сечения балки будет определяется зависимостью При

Для заданной балки

Площадь прямоугольника с основанием равна:

Поперечное сечение в форме круга. Для заданной балки Круг также является сечением простой геометрической формы. Осевой момент сопротивления круга диаметром равен:

Тогда, согласно (2.6) минимальный диаметр круглого поперечного сечения будет определяется зависимостью

Для заданной балки Площадь круга диаметром 18,7 см равна:

Поперечное сечение из двух швеллеров.

Швеллер является стандартным прокатным профилем. Поскольку выбираемое сечение состоит из двух швеллеров, согласно (б) минимальное значение момента сопротивления одного швеллера будет равно

Из справочных таблиц (ГОСТ 8239-86) выбираем швеллер №30, для которого

Площадь поперечного сечения из двух швеллеров будет равна

Все выбранные поперечные сечения являются равнопрочными так как способны воспринимать без разрушения одинаковую внешнюю нагрузку.

6. Сравним выбранные поперечные сечения по металлоемкости.

Поскольку балка является одноосным элементом, ее металлоемкость зависит от площади поперечного сечения. Сведем в таблицу площади выбранных поперечных сечений различной формы и сравним их с площадью двутавра

Сравнение площадей выбранных поперечных сечений показывает, что наиболее экономичным является двутавровое сечение. Площадь, следовательно, погонный вес и металлоемкость прямоугольного сечения в 3,103, круглого — в 4,431, а сечения из двух швеллеров — в 1,308 раза больше площади равнопрочного двутаврового сечения. Поэтому наиболее рациональной формой поперечного сечения при изгибе является двутавровое поперечное сечение.

На странице -> решение задач по сопротивлению материалов (сопромат) собраны решения задач и заданий с решёнными примерами по всем темам сопротивления материалов.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

iSopromat.ru

Пример решения задачи по расчету опорных реакций балки, закрепленной на двух шарнирных опорах и нагруженной сосредоточенной силой F, моментом m и равномерно распределенной нагрузкой q.

Задача

Для заданной двухопорной балки с консольной частью, нагруженной комплексом нагрузок: силой F, моментом m и распределенной нагрузкой q, определить величину и направление опорных реакций.

Расчетная схема балки показана на рис.1

Длина пролета балки 3м. Длина консольной части – 1,5м.

Пример решения

Рекомендуем посмотреть наш видеоурок. В нем мы постарались подробно показать порядок расчета реакций в опорах балки.

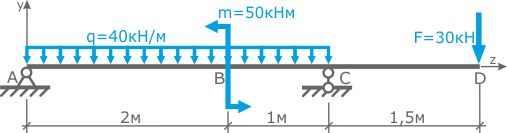
Для решения задачи, обозначим характерные точки (сечения) балки (точки A, B, C и D) и определим положение системы координат y-z, выбрав ее начало например в т. A (рис.2)

Обе опоры балки являются шарнирными, поэтому в каждой из них будет возникать только сила, обозначим их соответственно R_A и R_C

Так как все заданные нагрузки раположены исключительно в вертикальной плоскости (плоский поперечный изгиб) и не дают проекций на ось z, то опорные реакции будут тоже только вертикальными.

Вообще говоря, реакции в опорах являются такими силами, которые необходимы для удержания балки с приложенными к ней нагрузками, в статичном (неподвижном) состоянии. В данном случае эти силы не позволяют ей вращаться и перемещаться в вертикальной плоскости.

Данная балка является статически определимой, т.к. уравнений равновесия достаточно для определения неизвестных усилий в опорах балки.

Для составления уравнений статики, опорные реакции R_A и R_C предварительно направляются произвольно, например, вверх (рис.3).

Для определения двух неизвестных реакций потребуется два уравнения.

1. Балка не перемещается по вертикали, т.е. сумма проекций всех сил на ось y равна нулю:

Здесь сумму моментов лучше записывать относительно точки расположенной на опоре (например, A), т.к. в этом случае соответствующая реакция R_A в уравнении не участвует.

Из выражения (2) определяем R_C:

и подставив его в выражение (1) находим R_A:

Направление и величина реакций, как правило, необходимы для дальнейших расчетов балки на прочность и жесткость, поэтому во избежание возможных ошибок рекомендуется выполнять проверку найденных значений.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Определение реакций опор балки – решение задачи

Как определить реакции опор балки

Пример решения задачи на определение реакций опор балки

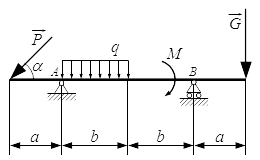
Жесткая балка, линейные размеры которой указаны на рисунке 1, закреплена в точках А и В. На балку действуют пара сил с моментом М, равномерно распределенная нагрузка интенсивностью q и две силы P и G, место приложения которых показано на рисунке.
Определить реакции опор балки в точках A и B, вызываемые указанными нагрузками.

Дано:
P = 20,2 Н ; G = 22,6 Н ; q = 2 Н/м ; M = 42,8 Н·м ; a = 1,3 м ; b = 3,9 м ; α = 45° ;

Решение задачи

Проводим оси x и y системы координат. Начало системы координат поместим в точку A . Ось x направим горизонтально, вдоль балки. Ось y – вертикально. Ось z перпендикулярна плоскости рисунка и направлена на нас. На рисунке она не указана.

Силы, действующие на балку.

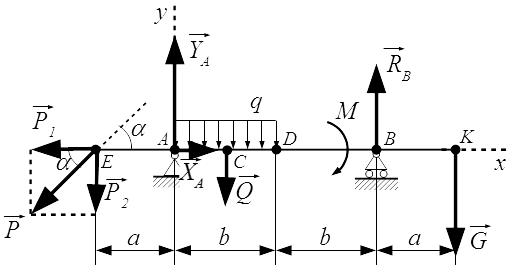
Отбрасываем опоры и заменяем их силами реакций.
В шарнире A , разложим силу реакции на составляющие и вдоль осей координат.
Реакция , в подвижной опоре на катках, направлена вертикально. Предполагаемые направления реакций опор выбираем по своему усмотрению, наугад. Если ошибемся с направлением реакции, то получим отрицательное значение, что будет говорить о том, что соответствующая сила реакции направлена в противоположную сторону.

Заменим равномерно распределенную нагрузку q равнодействующей . Абсолютное значение равнодействующей равно площади эпюры:
Н .
Точка приложения равнодействующей находится в центре тяжести эпюры. Поскольку эпюра представляет собой прямоугольник, то ее центр тяжести находится в точке C – посередине отрезка AD :
AC = CD = b/2 = 1,95 м .

Уравнения равновесия для сил

Определяем проекции сил на оси координат.

Разложим силу на составляющие вдоль координатных осей:
.
Абсолютные значения составляющих:
.
Вектор параллелен оси x и направлен в противоположную от нее сторону. Вектор параллелен оси y и также направлен в противоположную сторону. Поэтому проекции силы на оси координат имеют следующие значения:
.

Остальные силы параллельны осям координат. Поэтому они имеют следующие проекции:
;
;
;
;
.

Составляем уравнения равновесия для сил.
Сумма проекций всех сил на ось x равна нулю:
;
;
;
(П1) .

Сумма проекций всех сил на ось y равна нулю:
;
;
;
(П2) .

Уравнения равновесия для моментов

Итак, мы уже составили два уравнения для сил: (П1) и (П2). Но в них есть три неизвестные величины: , и . Чтобы их определить, нам нужно составить еще одно уравнение.

Составим уравнение равновесия для моментов сил. Для этого нам нужно выбрать ось, относительно которой мы будем вычислять моменты. В качестве такой оси возьмем ось, проходящую через точку A , перпендикулярно плоскости рисунка. За положительное направление выберем то, которое направлено на нас. Тогда, по правилу правого винта, положительным направлением закручивания будет направление против часовой стрелки.

Находим моменты сил относительно выбранной оси.
Силы , и пересекают ось. Поэтому их моменты равны нулю:
; ; .

Сила перпендикулярна плечу AB . Ее момент:
.
Поскольку, относительно оси A , сила направлена против часовой стрелки, то ее момент положительный.

Сила перпендикулярна плечу AK . Поскольку, относительно оси A , эта сила направлена по часовой стрелки, то ее момент имеет отрицательное значение:
.

Аналогичным способом находим моменты остальных сил:
;
.
Момент от пары сил M не зависит от точек приложения сил, входящих в пару:
.

Составляем уравнение равновесия. Сумма моментов сил относительно оси A равна нулю:
;

;
;
(П3) .

Решение уравнений равновесия

Итак, для трех неизвестных величин, мы получили три уравнения:
(П1) .
(П2) .
(П3) .

Решаем эти уравнения. Вычисляем расстояния.
м;
м;
м;
м.

Из уравнения (П1) находим:
Н.
Из уравнения (П3) находим:

Н.
Из уравнения (П2) имеем:
Н.
Абсолютное значение реакции опоры в точке A :
Н.

Проверка правильности решения

Чтобы проверить, правильно ли мы определили реакции опор балки, найдем сумму моментов сил относительно другой оси. Если мы нашли реакции правильно, то она должна равняться нулю.

Возьмем ось, проходящую через точку E . Вычисляем сумму моментов сил относительно этой оси:

.
Найдем погрешность вычисления суммы моментов. Найденные силы мы округлили до двух знаков после запятой. То есть погрешность определения реакций опор составляет 0,01 Н . Расстояния, по порядку величины, примерно равны 10 м. Тогда погрешность вычисления суммы моментов составляет около 10·0,01 = 0,1 Нм . Мы получили значение -0,03 Нм . Эта величина отличается от нуля не более, чем на величину погрешности. То есть, с учетом погрешности вычислений, сумма моментов относительно другой оси равна нулю. Значит решение правильное, силы реакций найдены верно.

Второй способ решения

Первым способом мы составили два уравнения для сил и одно – для моментов. Задачу можно решить другим способом, составив два уравнения для моментов и одно для сил.

Воспользуемся тем, что сумма моментов сил равна нулю относительно любой оси. Возьмем вторую ось, которая проходит через точку B перпендикулярно плоскости рисунка. Сумма моментов сил относительно этой равна нулю:
.
Вычисляем моменты сил относительно оси B .
; ; ;
;
;
;
;
.

Сумма моментов сил относительно оси B равна нулю:
;

;
;
(П4) ;

Итак, вторым способом, мы также имеем три уравнения:
(П1) .
(П3) ;
(П4) .

Здесь каждое уравнение содержит только одну неизвестную величину. Реакции и определяются из тех же уравнений, что и ранее. Находим силу из уравнения (П4):

Н.

Значение реакции совпало со значением, полученным первым способом из уравнения (П2).

Автор: Олег Одинцов . Опубликовано: 14-10-2017 Изменено: 28-12-2021