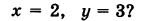Понятие об уравнении линии и поверхности. Полярная система координат.
Читайте также:
|
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Общее уравнение плоскости
- Угол между плоскостями
- Понятие о производной вектор-функции
- Криволинейные интегралы
- Прямоугольная система координат на плоскости и ее применение
- Линии второго порядка
- Полярные координаты
- Непрерывность функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Составить уравнения координатных линий поверхности
Поверхность. Способы задания поверхности. Регулярная параметризация поверхности. Координатные линии и координатная сеть на поверхности. Задача картографии. Касательная плоскость поверхности в ее гладкой точке. Нормаль поверхности в ее гладкой точке. Первая квадратичная форма поверхности. Длина дуги кривой на поверхности. Угол между кривыми на поверхности. Ортогональные траектории семейства кривых на поверхности. Площадь поверхности. Конформное отображение поверхностей. Изометрия поверхностей.
Основные определения, результаты, комментарии
Элементарной областью на плоскости переменных называется область, гомеоморфная кругу. Элементарной поверхностью в пространстве переменных называется множество точек пространства, гомеоморфное элементарной области на плоскости. Функциональное задание гомеоморфизма (рис. 20)
называется параметрическим представлением поверхности. Образы прямых вида и называются координатными линиями на поверхности (рис. 20) и задаются уравнениями
и каждой точке ставится в соответствие пара чисел , называемая криволинейными координатами.
Общей поверхностью называется подмножество евклидова пространства, локально гомеоморфное евклидовой плоскости. Необходимое и достаточное условие локальной гомеоморфности отображения, задаваемого в области плоскости переменных регулярными функциями
Очевидно, что общая поверхность допускает покрытие элементарными поверхностями.
Сеть координатных линий поверхности, или координатная сеть , называется правильной в точке , если в этой точке выполнено условие Нетрудно заметить, что частные производные и в данной точке представляют собой касательные векторы к координатным линиям и соответственно. Поэтому условие правильности координатной сети в точке требует, чтобы касательные векторы к координатным линиям в этой точке были неколлинеарны. В дальнейшем будут рассматриваться только такие точки на поверхности.
Будем называть поверхность -регулярной, если она обладает параметризацией , имеющей непрерывные частные производные
порядка , причем в каждой точке выполнено условие
Поверхность задана неявным уравнением если координаты каждой ее точки удовлетворяют этому уравнению.
Пусть и — две различные точки на поверхности . Касательной плоскостью поверхности в точке (рис. 21) называется плоскость , проходящая через точку и удовлетворяющая соотношению
Уравнение касательной плоскости поверхности в точке с криволинейными координатами (и декартовыми координатами ) может быть вычислено по одной из следующих формул:
| при параметрическом задании, |
| при неявном задании. |
Первое из уравнений означает, что векторы образуют базис касательных векторов в точке
Нормаль поверхности в точке — это прямая, ортогональная касательной плоскости, проведенной в этой точке поверхности. Уравнения нормали поверхности в точке с криволинейными координатами (и декар-
товыми координатами ) могут быть вычислены по формулам
| при неявном задании. |
Теперь мы можем дать геометрическую интерпретацию условию регулярности неявного задания кривой в пространстве. Поверхности и , имеющие общую точку , назовем пересекающимися трансверсально в точке , если их касательные плоскости, проведенные в этой точке, пересекаются .
Согласно известной теореме аналитической геометрии, для этого необходимо и достаточно, чтобы векторы нормали касательных плоскостей, а следовательно, векторы нормали поверхностей, были неколлинеарны в точке (рис. 22). Таким образом, условие максимальности ранга матрицы (6) — это условие трансверсальности пересечения поверхностей в точке.
Первой квадратичной формой поверхности называется скалярный квадрат первого дифференциала радиус-вектора ее точки :
где введены канонические обозначения
При этом коэффициенты являются функциями точки поверхности.
Первая квадратичная форма поверхности несет информацию о свойствах измерения длин, углов и площадей на поверхности, являясь своеобразным «справочником геодезиста». Первую квадратичную форму поверхности называют также метрической формой .
Так как в евклидовом пространстве скалярный квадрат любого ненулевого вектора строго положителен, то и первая квадратичная форма любой регулярной поверхности в евклидовом пространстве положительно определена , то есть , и невырождена , то есть только при
Длина кривой на поверхности может быть представлена криволинейным интегралом
Если кривая задана параметрическим способом , то первый дифференциал радиус-вектора точки вдоль этой кривой при подстановке , принимает вид
Подстановка полученного выражения в формулу длины кривой на поверхности приводит к результату (интеграл определенный!)
Тогда направление может быть указано «однородными координатами» . Очевидно взаимно однозначное соответствие
(и даже гомеоморфизм) множества направлений в точке поверхности и проективной прямой.
Углом между кривыми на поверхности (рис. 23), пересекающимися в точке , называется угол, образованный касательными направлениями к кривым в этой точке. Рассмотрим два направления и .
Угол между направлениями можно вычислять как угол между их представителями.
Его косинус равен
Направления и на поверхности ортогональны тогда и только тогда, когда . Пусть в окрестности точки на поверхности задано семейство кривых, представленных неявными уравнениями вида , где — постоянные, — дифференцируемая функция. Пусть в точке выполнено условие Линии семейства имеют в каждой точке рассматриваемой окрестности направление Тогда направление линии, ортогональной линиям семейства , удовлетворяет соотношению ортогональности
Полученное уравнение является дифференциальным уравнением семейства кривых, ортогональных семейству, заданному уравнениями
.
Площадь части поверхности, задаваемой параметрическим уравнением , определенным на компактной области плоскости переменных , с кусочно гладкой границей , вычисляют по формуле:
Гомеоморфизм поверхностей называется изометрией , если поверхности и можно параметризовать так, что первая квадратичная форма поверхности в любой точке равна первой квадратичной форме поверхности в точке
Очевидно, соответственные кривые изометричных поверхностях имеют равные длины. Обратное также верно. Кроме этого, на изометричных поверхностях углы между соответственными кривыми равны, и площади соответственных областей также равны.
Также имеется важный класс гомеоморфизмов поверхностей, включающий в себя изометрии. Гомеоморфизм поверхностей называется конформным отображением , если для любых пересекающихся кривых и на поверхности образуемый ими угол равен углу между кривыми и на поверхности . Очевидно, всякая изометрия является конформным отображением.
1. Цилиндрическая система координат в пространстве задается так, как показано на рис. 24 а).
Напишите выражение декартовых координат
точки через ее цилиндрические координаты и правила обратного перехода. Составьте параметрическое представление прямого кругового цилиндра радиуса , ось которого совпадает с осью аппликат. Изобразите на рисунке вид координатных линий построенного параметрического представления. Исследуйте это представление на регулярность.
2. Сферическая система координат в пространстве задается так, как показано на рис. 24 б). Напишите выражение декартовых координат точки через ее сферические координаты и правила обратного перехода. Составьте параметрическое представление сферы радиуса , центр которой совмещен с началом координат. Изобразите на рисунке вид координатных линий построенного параметрического представления. Исследуйте это представление на регулярность. Во всех ли точках сферы координатная сеть правильна?
3. Дано параметрическое представление поверхности. Определите и изобразите на рисунке вид поверхности и координатные линии. Укажите область изменения параметров. Правильная ли на этой поверхности координатная сеть?
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
4. Поверхность вращения. Кривая расположенная в плоскости , вращается вокруг оси . Составьте уравнение поверхности, образуемой этой кривой. Докажите, что нормаль поверхности вращения расположена в плоскости, проходящей через ось вращения.
Кривую назовем образующей поверхности вращения.
5. Составьте параметрическое задание поверхности вращения с осью и образующей :
1) ;
2) ;
3) .
6. Поверхность переноса. Две кривые и пересекаются в точке , такой, что , трансверсально , то есть . Кривая перемещается поступательно так, что ее точка скользит по кривой . Заметаемая ею поверхность называется поверхностью переноса.
1) Составьте параметрическое представление этой поверхности. Изменится ли вид поверхности переноса, если кривые и поменять ролями?
2) Докажите, что касательные плоскости поверхности переноса вдоль координатной линии параллельны некоторой прямой.
3) Докажите, что параболоиды являются поверхностями переноса.
Указание. В качестве кривых и выберите параболы, расположенные во взаимно ортогональных плоскостях.
7. Обобщенная цилиндрическая поверхность. В условии предыдущей задачи считайте линию прямой, параллельной вектору . Получаемая таким способом поверхность переноса называется обобщенной цилиндрической поверхностью. Постройте ее параметрическое представление и уравнение семейства касательных плоскостей к цилиндрической поверхности в тех ее точках, в которых . Что можно сказать о касательных плоскостях цилиндрической поверхности?
8. Обобщенная коническая поверхность образована всеми прямыми, пересекающими данную кривую и проходящими через точку , При этом кривая называется направляющей , а прямые — образующими конической поверхности. Составьте параметрическое представление конической поверхности и уравнение семейства касательных плоскостей к конической поверхности в тех ее точках, в которых . Что
можно сказать о касательных плоскостях конической поверхности?
9. Винтовая поверхность. Прямая вращается вокруг оси и одновременно перемещается вдоль нее так, что перемещение пропорционально углу поворота. Описываемая этой прямой поверхность называется винтовой поверхностью. Напишите параметрическое представление винтовой поверхности и дайте ее изображение.
10. Обобщенная винтовая поверхность. В условии предыдущей задачи замените прямую линией , . Напишите параметрическое представление описываемой поверхности. Полагая
1) ; 2) ,
напишите параметрические представления и дайте изображения полученных поверхностей.
11. Трубчатая поверхность образована всеми окружностями постоянного радиуса с центрами на кривой расположенными в нормальных плоскостях этой кривой. Считая, что — естественный параметр кривой, кривизна кривой отлична от нуля и , составьте параметрическое представление трубчатой поверхности.
Решение. (рис. 25) Представим радиус — вектор точки поверхности в виде суммы где — полярный угол в нормальной плоскости
кривой , отсчитываемый от главной нормали по направлению к бинормали, — соответствующий «полярный радиус». Тогда где и — единичные векторы главной нормали и бинормали в точке, соответствующей значению естественного параметра. Заметим, что в естественной параметризации и
Эти уравнения позволяют выразить единичные
направляющие векторы трехгранника Френе через производные вектора
Подстановка в выражение для радиус — вектора приводит к окончательному выражению
Докажите, что нормаль трубчатой поверхности пересекает кривую и является ее нормалью.
Указание. Воспользуйтесь формулами Френе.
Составьте параметрическое представление трубчатой поверхности, если
1$»>, а радиус образующей окружности .
12. Докажите, что сумма квадратов отрезков, отсекаемых на осях координат касательной плоскостью поверхности , не зависит от выбора точки на поверхности.
13. Докажите, что касательные плоскости к поверхности образуют с координатными плоскостями тетраэдры постоянного объема.
14. Докажите, что касательные плоскости к поверхности в точках образуют пучок плоскостей.
15. Дана кривая , где — естественный параметр. Найдите первую квадратичную форму поверхности, образованной
1) касательными к кривой ;
2) главными нормалями;
3) бинормалями кривой .
16. На поверхности, образованной касательными к кривой , где — естественный параметр,
1) составьте дифференциальное уравнение ортогональных траекторий к семейству прямолинейных образующих;
2) напишите дифференциальное уравнение линий, пересекающих прямолинейные образующие под постоянным углом ;
3) убедитесь в том, что область этой поверхности наложима на плоскость.
17. Дан прямой геликоид .
1) Вычислите его первую квадратичную форму.
2) Найдите угол между координатными линиями как функцию точки.
3) Составьте уравнение биссекторных линий для линий координатной сети.
4) Проверьте, что сеть, дифференциальное уравнение которой имеет вид
, ортогональна.
5) Вычислите площадь четырехугольника, ограниченного линиями , , , .
6) Покажите, что прямой геликоид наложим на катеноид с образующей
, , ( ) .
18. Дан прямой круговой цилиндр .
1) Вычислите его первую квадратичную форму.
2) Найдите угол между координатными линиями как функцию точки.
3) Составьте уравнения линий, пересекающих образующие под постоянным углом.
4) Найдите уравнение ортогональных траекторий семейства линий
.
5) Вычислите площадь треугольника, ограниченного линиями
.
6) Докажите, что прямой круговой цилиндр наложим на плоскость.
19. Представление псевдосферы имеет вид
1) Вычислите ее первую квадратичную форму.
2) Найдите на псевдосфере линии, пересекающие меридианы под постоянным углом (локсодромы).
3) Найдите площадь поверхности псевдосферы.
4) Вычислите длину дуги линии между точками
20. Дана сфера
а) Найдите ее первую квадратичную форму.
б) Напишите уравнения ортогональных траекторий семейства линий
.
в) Составьте уравнение локсодромы — линии на сфере, которая пересекает меридианы под постоянным углом .
http://www.evkova.org/uravneniya-poverhnosti-i-linii-v-prostranstve
http://cito-web.yspu.org/link1/metod/met21/node8.html




 должен быть одинаков со знаком y, а знак
должен быть одинаков со знаком y, а знак  — со знаком х.
— со знаком х.
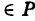
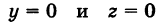
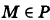 обозначает, что точка М принадлежит Р. Формула
обозначает, что точка М принадлежит Р. Формула 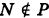 обозначает, что точка N не принадлежит Р.
обозначает, что точка N не принадлежит Р.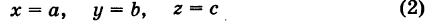
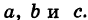
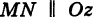 (образующая) вдоль заданной линии L, лежащей в плоскости Оху (направляющая) (рис. 190).
(образующая) вдоль заданной линии L, лежащей в плоскости Оху (направляющая) (рис. 190).

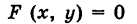
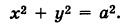
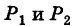 (рис. 192). Точка
(рис. 192). Точка  , лежащая на линии L, принадлежит как поверхности
, лежащая на линии L, принадлежит как поверхности 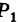 так и поверхности
так и поверхности 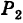 , и, следовательно, координаты этой точки удовлетворяют уравнениям обеих поверхностей.
, и, следовательно, координаты этой точки удовлетворяют уравнениям обеих поверхностей.
 называется такая пара уравнений между переменными
называется такая пара уравнений между переменными  , которой удовлетворяют координаты каждой точки, лежащей на данной линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.
, которой удовлетворяют координаты каждой точки, лежащей на данной линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.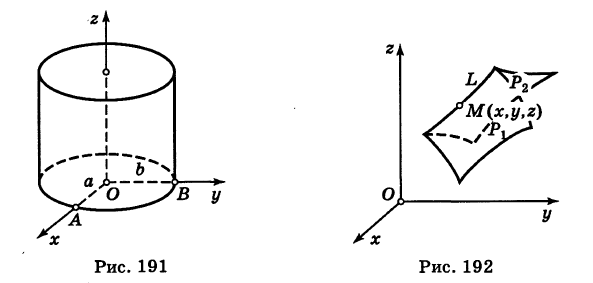
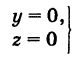
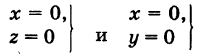
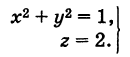
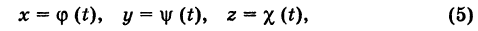
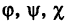 — некоторые определенные функции. Обобщая уравнения (5), под t понимают вспомогательную переменную (параметр)> не обязательно время; поэтому уравнения (5) носят название параметрических уравнений линии в пространстве.
— некоторые определенные функции. Обобщая уравнения (5), под t понимают вспомогательную переменную (параметр)> не обязательно время; поэтому уравнения (5) носят название параметрических уравнений линии в пространстве. (рис. 195).
(рис. 195).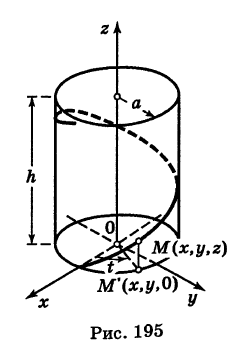
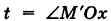 и учитывая, что аппликата г винтовой линии растет пропорционально углу поворота t, будем иметь
и учитывая, что аппликата г винтовой линии растет пропорционально углу поворота t, будем иметь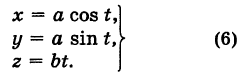
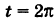 ; тогда
; тогда 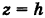 . Следовательно,
. Следовательно,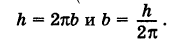

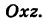 . Из уравнений (6′) также вытекает, что проекция винтовой линии (6′) на координатную плоскость Оху есть окружность, а на координатную плоскость
. Из уравнений (6′) также вытекает, что проекция винтовой линии (6′) на координатную плоскость Оху есть окружность, а на координатную плоскость 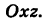 — косинусоида.
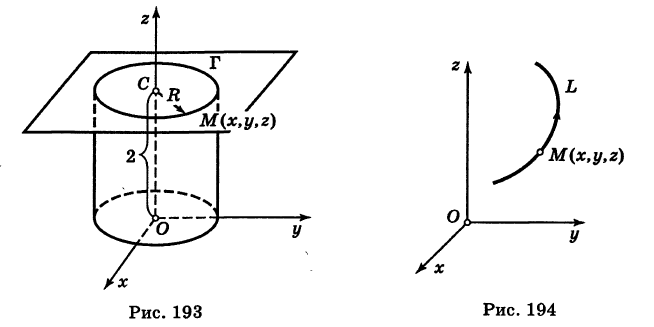
— косинусоида.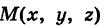 кривой L можно характеризовать ее радиусом-вектором («следящий радиус-вектор») (рис. 196)
кривой L можно характеризовать ее радиусом-вектором («следящий радиус-вектор») (рис. 196)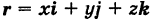
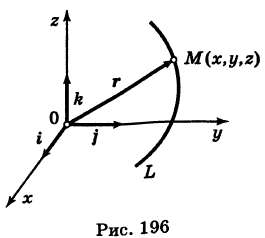
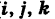 — орты). Тогда из (5) получаем векторное уравнение линии
— орты). Тогда из (5) получаем векторное уравнение линии
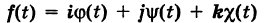

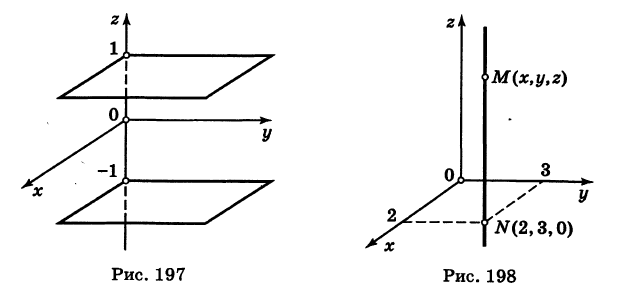
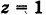 или
или 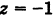 . Следовательно, графиком уравнения (8) является пара плоскостей, параллельных координатной плоскости Оху и отстоящих от нее на расстояниях, равных единице (рис. 197).
. Следовательно, графиком уравнения (8) является пара плоскостей, параллельных координатной плоскости Оху и отстоящих от нее на расстояниях, равных единице (рис. 197).