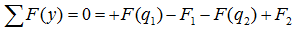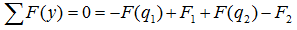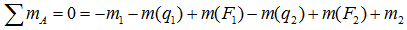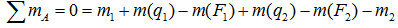iSopromat.ru

Правила знаков для моментов и проекций сил на оси координат:

Правило знаков проекций сил

То есть, для уравнений сумм проекций сил на оси:
Проекции сил и нагрузок на координатную ось имеющие одинаковое направление принимаются положительными, а проекции усилий противоположного направления – отрицательными.

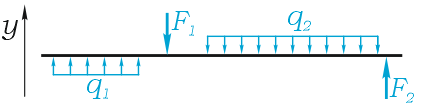
Например, для такой схемы нагружения:

уравнение суммы сил имеет вид

А так как суммы проекций разнонаправленных сил равны, то данное уравнение можно записать и так:

Здесь F(q) – равнодействующая от распределенной нагрузки, определяемая произведением интенсивности нагрузки на ее длину.

Правило знаков для моментов

Сосредоточенные моменты и моменты сил стремящиеся повернуть систему относительно рассматриваемой точки по ходу часовой стрелки записываются в уравнения с одним знаком, и соответственно моменты, имеющие обратное направление с противоположным знаком.

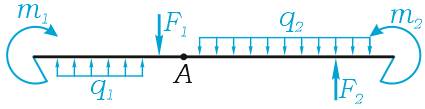
Например, для суммы моментов относительно точки A

или, что одно и то же

Здесь m(F) – моменты сил F относительно точки A.
M(q) – моменты распределенных нагрузок q относительно рассматриваемой точки.

При составлении уравнений статики для систем находящихся в равновесии (например при определении опорных реакций) правила знаков могут быть упрощены до следующего вида:
Нагрузки направленные в одну сторону принимаются положительными, а соответственно, нагрузки обратного направления записываются со знаком минус.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Теоретическая механика:
Пространственная система сил

Смотрите также решения задач по теме «Пространственная система сил» в онлайн решебниках Яблонского и Мещерского.

При решении задач, приведенных в этой главе, необходимо использовать не две оси координат, которые всегда можно расположить в одной плоскости – в плоскости рисунка, иллюстрирующего задачу, а три взаимно перпендикулярные оси.

Эти оси нельзя расположить в одной плоскости и при изображении пространственной системы сил на рисунке надо использовать одну из принятых в машиностроительном черчении аксонометрических проекций (ГОСТ 2.305–68. Изображения – виды, разрезы, сечения).

На рис. 145 показано изображение трех взаимно перпендикулярных плоскостей в изометрической проекции. Пересечение двух вертикальных плоскостей определяет положение вертикальной оси z, пересечением обеих вертикальных плоскостей с горизонтальной определяются положения двух горизонтальных осей х и у.

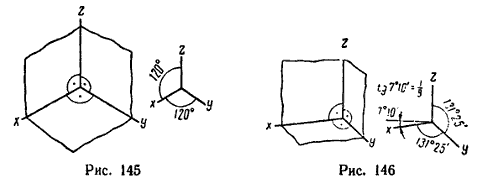
На рис. 146 представлены те же три взаимно перпендикулярные плоскости в диметрической проекции, а на рис. 147 – в фронтальной диметрическои проекции. На каждом рисунке справа показано положение осей при изображении соответствующей проекции.

Если при решении задач, в которых рассматривается пространственная система сил, трудно представить взаимное расположение сил или их расположение относительно выбранных осей координат, то следует изготовить из плотной бумаги модель трех пересекающихся под прямым углом плоскостей, а линии пересечения плоскостей выделить цветными линиями и обозначить их соответственно х, у и z. В такой модели трех взаимно перпендикулярных осей можно помещать модели систем сил, рассматриваемых в задаче, изготовленные из пластилина, проволочек и спичек.

§ 18. Правило параллелепипеда сил

Простейшую пространственную систему сходящихся сил образуют три силы, приложенные к одной точке.

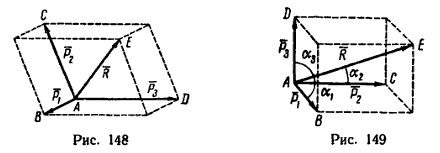
Для сложения таких трех сил применяется правило параллелепипеда (рис. 148). Если даны силы P₁, P₂ и P₃, то заменяющая их действие равнодействующая R по модулю и направлению соответствует диагонали АЕ параллелепипеда, ребра которого AB, АС и AD соответствуют трем силам.

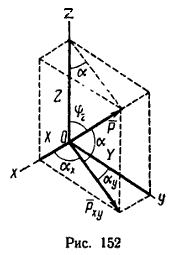
В частном случае, который наиболее характерен для решения практических задач, три данные силы P₁, P₂ и P₃ взаимно перпендикулярны и тогда при их сложении образуется прямоугольный параллелепипед (рис. 149).

В этом случае модуль равнодействующей
R = sqrt(P₁ 2 + P₂ 2 + P₃ 2 )
а направление R относительно каждой из составляющих сил можно найти по формулам
cos α₁ = P₁/R; cos α₂ = P₂/R; cos α₃ = P₃/R.

Так же как и правило параллелограмма (см. § 1, 5 и 6), правило параллелепипеда можно использовать не только при сложении сил, но и при разложении данной силы на три составляющие. Наиболее часто производят разложение силы на составляющие, действующие по трем взаимно перпендикулярным направлениям.

§ 19. Проекция силы на три взаимно перпендикулярные оси. Определение равнодействующей системы пространственных сил, приложенных к точке

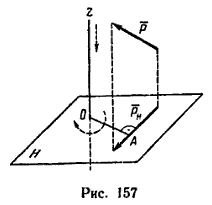
Если требуется определить проекции силы Р на три взаимно перпендикулярные оси (рис. 152), то обычно силу проектируют сначала на одну из плоскостей (например, горизонтальную), а уже затем на оси, расположенные в этой плоскости. При этом нужно обратить внимание на то, что в отличие от проекций силы на оси, являющихся скалярами, проекция силы на плоскость (P_xy на рис. 152) – величина векторная (Е. М. Никитин, § 38).

Легко заметить, что на трех взаимно перпендикулярных проекциях можно построить прямоугольный параллелепипед, диагональю которого является проектируемый вектор.

Из рис. 152 видно, что проекция на горизонтальную плоскость
P_xy = P cos α,
поэтому
X = P cos α cos α_x; Y = P cos α cos α_y и Z = P cos φ_z.

Если же известны углы φ_x и φ_y (на рисунке они не показаны), образуемые вектором Р с осями х и у, то его проекции на эти оси соответственно равны
X = P cos φ_x и Y = P cos φ_y.

При помощи проекций сил на три оси легко определить равнодействующую системы сил, приложенных к точке.

Для этого необходимо:

1) выбрать расположение осей так, чтобы проекции всех сил определились простейшим образом;

2) найти проекции всех сил на каждую из осей;

3) сложить проекции всех сил на каждую из осей и найти таким образом три проекции искомой равнодействующей на оси:
X_R = ∑ X_i; Y_R = ∑ Y_i и Z_R = ∑ Z_i;

4) определить модуль равнодействующей R:
R = sqrt(X_R 2 + Y_R 2 + Z_R 2 );

5) определить направление равнодействующей, найдя какие-либо два угла из трех:
cos φ_x = X_R/R; cos φ_y = Y_R/R; cos φ_z = Z_R/R.

§ 20. Равновесие пространственной системы сходящихся сил

Если система сходящихся сил уравновешена, то ее равнодействующая R=0, а это означает, что и проекции равнодействующей на три взаимно перпендикулярные оси равны нулю (X_R=0, Y_R=0, Z_R=0). Отсюда образуются три уравнения равновесия:
∑ X_i = 0;
∑ Y_i = 0;
∑ Z_i = 0.

При помощи этих уравнений и решаются задачи на равновесие пространственной системы сходящихся сил.

Уравнений равновесия – три, следовательно, статически определимой является такая пространственная система сходящихся сил, в которой неизвестных сил не более трех.

§ 21. Момент силы относительно оси

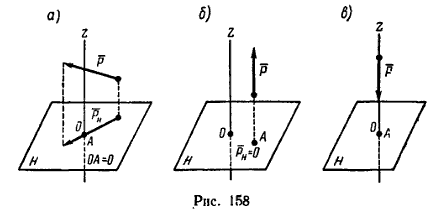
Чтобы определить момент силы Р относительно заданной или выбранной оси, например оси z (рис. 157), необходимо выполнить следующие операции:

1) расположить плоскость Н перпендикулярно оси z;

2) определить проекцию силы Р на плоскость H – найти P_H;

3) из точки пересечения оси с плоскостью (из точки О) провести перпендикуляр к направлению проекции P_H и определить длину этого перпендикуляра OA – плечо силы P_H;

4) определить знак момента, придерживаясь такого правила: посмотрим на плоскость Н со стороны положительного направления оси, если увидим, что проекция P_H поворачивает плечо против хода часовой стрелки, значит момент имеет положительный знак; а если проекция P_H поворачивает плечо по часовой стрелке (как это показано, например, на рис. 157), момент имеет отрицательный знак;

5) находим числовое значение момента силы Р относительно оси; для этого P_H – модуль проекции силы Р на плоскость, перпендикулярную к оси, умножаем на плечо OA.

Таким образом (см. рис. 157)
M_z(P) = -P_H * OA.

Момент силы относительно оси, так же как и момент силы относительно точки, измеряется по Международной системе (СИ) в ньютон-метрах (Н*м), а по технической системе (МКГСС) – в кГ*м.

Для успешного решения задач и облегчения составления уравнений моментов относительно осей нужно иметь в виду три частных случая, в которых момент силы относительно оси равен нулю (рис. 158):

Случай 1-й (рис. 158, а). Сила Р или линия ее действия пересекает ось; в этом случае плечо OA=0, поэтому P_H*OA=0.

Случай 2-й (рис. 158, б). Линия действия силы Р параллельна оси; в этом случае P_H=0, поэтому P_H*OA=0.

Случай 3-й (рис. 158, в). Линия действия силы Р совпадает с осью; в этом случае и P_H=0 и плечо OA=0.

§ 22. Равновесие произвольной пространственной системы сил

Произвольную пространственную систему сил, так же как и плоскую, можно привести к одной точке и заменить главным вектором R_гл и главным моментом M_гл. Только в этом случае линия действия главного вектора может находиться не в плоскости действия главного момента.

Если R_гл=0 и M_гл=0, то система сил уравновешена и отсюда образуется система шести уравнений равновесия:
∑ X_i = 0;
∑ Y_i = 0;
(1) ∑ Z_i = 0;
∑ M_x(P_i) = 0;
∑ M_y(P_i) = 0;
∑ M_z(P_i) = 0.

Первые три уравнения (уравнения проекций) получены из условия R_гл=0. Если главный вектор равен нулю, то и алгебраические суммы проекций всех сил на каждую из осей также равны нулю.

Последние три уравнения (уравнения моментов) получены из условия M_гл=0. Если главный момент системы сил равен нулю, то алгебраические суммы моментов сил относительно каждой из осей равны нулю.

Для облегчения составления уравнений равновесия тело, равновесие которого рассматривается, целесообразно изображать вместе с действующими на него силами в проекциях на три основные плоскости, т. е. изображать вид спереди, вид сверху и один боковой вид – вид слева или вид справа (см. задачи 115, 116 и 117).

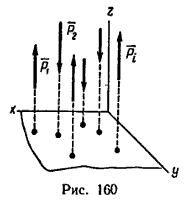
В частном случае линии действия сил, образующих пространственную систему, могут оказаться параллельными. Тогда одну из осей (например, ось z) выгодно расположить параллельно силам (рис. 160), а две другие оси расположатся в плоскости, перпендикулярной к линиям действия сил.

Легко понять, что для уравновешенной пространственной системы параллельных сил вместо шести уравнений можно составить лишь три: алгебраическую сумму проекций сил на ось, параллельную данным силам, и два уравнения моментов относительно двух других осей. Остальные уравнения превратятся в тождество вида 0=0.

В соответствии с расположением осей (см. рис. 160) уравнения равновесия имеют вид:
∑ Z_i = 0;
(2) ∑ M_x(P_i) = 0;
∑ M_y(P_i) = 0.

Для пространственной системы параллельных сил можно составить лишь три уравнения равновесия, поэтому, чтобы задача была статически определимой, в ней должно содержаться не более трех неизвестных сил.

В следующих задачах рассматриваются системы сил, произвольно расположенные в пространстве.

Одной из типичных задач, в которых применяются уравнения равновесия пространственной системы сил, является задача определения реакций опор вала какой-либо машины.

Задачи этого типа можно решать так же, как задачи 115 или 116, т. е. при помощи проекций вала вместе с векторами заданных и искомых сил на три взаимно перпендикулярные плоскости. Но в некоторых случаях оказывается более рациональным несколько иной прием решения, основанный на приведении сил к оси вала. В качестве примера для такого решения возьмем вал одного из многочисленных видов редукторов (редуктором называется механическое устройство для передачи мощности от двигателя, вал которого вращается с большой скоростью, к рабочей машине, вал которой имеет скорость вращения, в несколько раз меньшую).

Техническая механика

Пространственная система сил

Пространственная система сходящихся сил

Система сил, линии действия которых расположены в различных плоскостях, называется пространственной системой сил .

Пространственная система сил называется сходящейся , если линии действия всех сил системы пересекаются в одной точке.

Теорема: пространственная система сходящихся сил эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.

Пусть дана пространственная система n сходящихся сил (F₁, F₂, F₃. F_n) . На основании следствия из аксиом III и IV перенесем все силы системы вдоль линий действия в точку их пересечения. Затем на основании аксиомы параллелограмма последовательно сложим все силы и получим их равнодействующую:

Силовой многоугольник пространственной системы сил не лежит в одной плоскости, поэтому геометрический и графический способы нахождения равнодействующей пространственной системы сходящихся сил неприемлемы, а применяется только аналитический способ (метод проекций) .

Проекция силы на ось в пространстве находится по проецирующим перпендикулярам, и может быть определена при помощи тригонометрических функций. При определении проекций сил пространственной системы потребуется система координат с осями X , Y , Z , поскольку силы системы не располагаются в одной плоскости.

Правило знаков для проекций будет таким же, как и для плоской системы сил – совпадающие по направлению с координатной осью силы считаются положительными, в противном случае – отрицательными. Если вектор силы параллелен какой-либо оси координат, то он проецируется на эту ось в натуральную величину, если же вектор перпендикулярен оси, его проекция на эту ось будет равна нулю.

Разложение силы по трем осям координат

Пусть дана сила F (см. рисунок 1) .
Возьмем систему координат так, чтобы начало координат совпадало с началом вектора силы F (т. е. с точкой приложения силы). Из конца этого вектора опустим перпендикуляр на плоскость xy и разложим силу F на составляющие F_xy и F_z , а составляющую F_xy – на составляющие F_x и F_y . Тогда:

Достроим полученное изображение до параллелепипеда, у которого составляющие F_x , F_y и F_z являются ребрами, а сила F – диагональю.

Из изложенного можно сделать вывод: равнодействующая трех взаимно-перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах .

Из рисунка видно, что в случаях разложения силы F по трем взаимно-перпендикулярным направлениям x , y , z составляющие F_x , F_y и F_z равны по модулю проекциям силы F на эти оси.

Зная проекции силы на три взаимно-перпендикулярные оси координат, можно определить модуль и направление вектора силы по формулам:

модуль силы: F = √(F_x 2 + F_y 2 + F_z 2 ) (здесь и далее √ — знак корня) ;

направляющие косинусы: cos(F,x) = Fx/F; cos(F,y) = Fy/F; cos(F,z) = Fz/F .

Аналитический способ определения равнодействующей пространственной системы сходящихся сил

Рассмотренный выше способ разложения силы F на три составляющие по направлению координатных осей x , y , z можно применить для каждой из сходящихся сил пространственной системы. Тогда вместо данной системы n сходящихся сил мы получим эквивалентную ей систему 3n сил, из которых n сил действуют по оси x , n сил – по оси y , и n сил – по оси z .
Равнодействующая проекций сил системы на ось x равна их геометрической сумме, то же самое можно сказать и о равнодействующих проекций сил на оси y и z .
Таким образом, систему 3n сил можно заменить эквивалентной ей системой трех сил, каждая из которых представляет собой равнодействующую проекций сил данной системы на ту или иную ось координат.

Проекции силы на три взаимно-перпендикулярные оси и составляющие силы, направленные по этим осям, равны по модулю, следовательно, проекции равнодействующей равны:

Очевидно, что равнодействующая трех взаимно перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах, и по известным проекциям равнодействующей можно определить модуль и направление самой равнодействующей.

Аналитические условия равновесия пространственной системы сходящихся сил

Известно, что пространственная система сходящихся сил эквивалентна равнодействующей. Если такая система сил находится в равновесии, т. е. эквивалентна нулю, то можно сделать вывод, что равнодействующая этой системы равна нулю, а следовательно, и проекции равнодействующей тоже равны нулю, причем эти проекции равны сумме проекций составляющих.
Отсюда вытекают условия равновесия пространственной системы сходящихся сил:

ΣX = 0; ΣY = 0; ΣZ = 0 .

Эти условия формируются следующим образом: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую их трех координатных осей равнялась нулю.

Момент силы относительно оси

Рассмотрим колесо червячной передачи, укрепленное на валу, вращающемся в подшипниках (см. рисунок 2) . Червяк передает червячному колесу силу F , не лежащую в плоскости, перпендикулярной оси.

Разложим силу F на три взаимно-перпендикулярные составляющие F₁ , F₂ и F₃ .
Составляющую F₁ назовем окружной силой , составляющую F₂ – осевой силой , а составляющую F₃ – радиальной силой .
Из рисунка видно, что составляющая F₁ вызывает вращательное действие, которое измеряется произведением силы F₁ на радиус колеса r ; составляющая F₂ стремится сдвинуть червячное колесо вдоль оси, а составляющая F₃ стремится изогнуть ось колеса.
Очевидно, что вращающее действие сил F₂ и F₃ относительно оси колеса равно нулю.
Таким образом, если нужно найти момент силы относительно оси, то следует принимать в расчет только составляющую F₁ , лежащую в плоскости, перпендикулярной оси, и не пересекающую ось (иначе ее момент будет равен нулю).

Ранее было отмечено, что проекция вектора силы на ось есть скалярная алгебраическая величина. В отличие от проекции на ось проекция силы на плоскость есть величина векторная, так как эта проекция характеризуется не только числовым значением, но и положением на плоскости, т. е. направлением.
Поэтому моменту силы относительно оси можно дать такое определение: моментом силы относительно оси называется величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.

Это определение поясняет рисунок 3 .
Момент силы относительно оси условимся записывать следующим образом:

Условимся считать момент силы положительным, если смотреть с положительного конца оси и сила стремится вызвать вращение против часовой стрелки, если же сила стремится вызвать вращение по часовой стрелке, ее момент считаем отрицательным.

Момент силы относительно оси не меняется при перемещении силы вдоль оси ее действия.

Момент силы будет равен нулю в двух случаях (не считая случаев, когда сила равна нулю или направлена вдоль оси):

• если вектор силы параллелен оси, так как при этом проекция силы на плоскость, перпендикулярную оси, равна нулю (см. рисунок 3, сила F_Z) ;
• если линия действия силы пересекает ось, так как при этом плечо равно нулю (сила F₃ на рисунке 2) .

Аналитические условия равновесия пространственной системы произвольно расположенных сил

Пространственная система сил, в которой линии действия составляющих сил расположены произвольно, т. е. линии их действия могут не пересекаться и находиться в разных плоскостях, называется произвольно расположенной системой сил.

Для равновесия пространственной системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую из трех осей координат была равна нулю и чтобы алгебраическая сумма моментов всех сил относительно каждой из этих осей была равна нулю.

Строгое обоснование приведенного выше условия равновесия пространственной системы произвольно расположенных сил требует знания некоторых вопросов, не предусмотренных программами учреждений среднего профессионального образования, поэтому условие равновесия такой системы здесь приводится без доказательства.

Математически условие равновесия пространственной системы произвольно расположенных сил можно записать в виде уравнений:

• ΣX = 0; ΣMx(Fi) = 0;
• ΣY = 0; ΣMy(Fi) = 0;
• ΣZ = 0; ΣMz(Fi) = 0.

Свободное тело в пространстве имеет шесть степеней свободы, а именно: возможность перемещаться в направлениях трех взаимно-перпендикулярных осей координат и возможность вращаться вокруг этих осей. Таким образом, шести степеням свободы тела в пространстве соответствуют шесть условий равновесия.
Если система сил, приложенных к свободному телу, удовлетворяет всем шести условиям равновесия, то возможность трех перемещений и трех вращений тела под действием сил системы исключена, поэтому тело будет находится в равновесии.

Очевидно, что все выведенные ранее условия равновесия для различных систем сил являются частными случаями условия равновесия пространственной системы произвольно расположенных сил.

Так как условия равновесия пространственной системы сил справедливы для любых прямоугольных осей координат, то при решении данной задачи систему координат можно изменять, т. е. часть уравнений равновесия составить для одних осей координат, а часть – для измененных. В некоторых случаях этот прием упрощает решение задач.

Теорема о моменте равнодействующей относительно оси
(теорема Вариньона)

Теорема: момент равнодействующей относительно оси равен алгебраической сумме моментов, составляющих сил относительно этой же оси .

Пусть даны пространственная система n произвольно расположенных сил, приложенных к телу, и равнодействующая этой системы сил F_Σ (см. рисунок 4) :

Приложим к телу другую систему сил, равнодействующая которой F’_Σ по модулю равна F_Σ и направлена по той же линии действия, но в противоположную сторону, т. е. является уравновешивающей данной системы сил.
Тогда можно записать:

Так как обе записанные выше системы сил эквивалентны нулю, т. е. уравновешены, то к ним можно применить любое условие равновесия, например

Запишем это условие для обеих систем:

Так как правые части этих равенств равны, то будут равны и левые :

Сократив общее слагаемое M_x(F’_Σ) , получим: