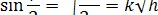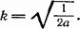Основные свойства касательной и нормали к циклоиде
3. Основные свойства касательной и нормали к циклоиде
Непосредственно очевидно, что ∟DOM равен 90° — φ.
Значит, ∟OMP = 90° — φ. Таким образом, получаем:
∟РМТ = ∟ОМТ — ∟ ОМР = 90° — 
Получается замечательный результат: угол РМТ оказывается равным углу РМЕ (см. теорему 2). Следовательно, прямые ME и МТ сольются! Наш рис. 18 сделан не совсем правильно! Правильное расположение линий дано на рис. 19.
Сформулируем полученный результат виде теоремы 3.
Теорема 3 (первое основное свойство циклоиды). Нормаль к циклоиде проходит через «нижнюю» точку производящего круга.
Из этой теоремы получается простое следствие. Угол между касательной и нормалью, по определению, — прямой. Это угол, вписанный в окружность производящего круга. Поэтому он должен опираться на диаметр круга. Итак, ТТ1— диаметр, и T1 — «верхняя» точка производящего круга. Сформулируем полученный результат.
Следствие (второе основное свойство циклоиды). Касательная к циклоиде проходит через «верхнюю» точку производящего круга.
Что бы объяснить это свойство нам необходимо построить циклоиду.
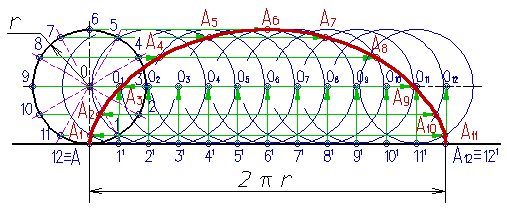
Построение циклоиды производится в следующей последовательности:
1. На направляющей горизонтальной прямой откладывают отрезок АА12, равный длине производящей окружности радиуса r, (2πr);
2. Строят производящую окружность радиуса r, так чтобы направляющая прямая была касательной к неё в точке А;
3. Окружность и отрезок АА12 делят на несколько равных частей, например на 12;
4. Из точек делений 1 1 , 2 1 , . 12 1 восстанавливают перпендикуляры до пересечения с продолжением горизонтальной оси окружности в точках 01, 02, . 012;
5. Из точек деления окружности 1, 2, . 12 проводят горизонтальные прямые, на которых делают засечки дугами окружности радиуса r;
6. Полученные точки А1, А2, . А12 принадлежат циклоиде.
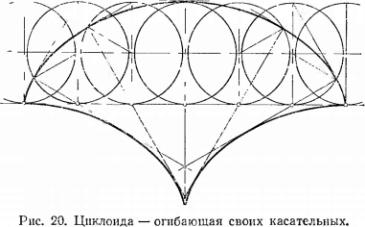
На рис. 20 основание циклоиды разделено на 6 равных частей;
чем число делений будет больше, тем, как мы знаем, чертеж получится точнее. В каждой точке циклоиды, построенной нами, проведем касательную, соединяя точку кривой с «верхней» точкой производящего круга. На нашем чертеже получилось семь касательных (из них две — вертикальные). Проводя теперь циклоиду от руки, будем заботиться, чтобы она действительно касалась каждой из этих касательных: это значительно увеличит точность чертежа. При этом сама циклоида будет огибать все эти касательные [1] ).
Проведем на том же рис. 20 нормали во всех найденных точках циклоиды. Всего будет, не считая направляющей, пять нормалей. Можно построить от руки сгибающую этих нормалей. Если бы мы вместо шести взяли 12 или 16 точек деления, то нормалей на чертеже было бы больше, и огибающая наметилась бы ясней. Такая огибающая всех нормалей играет важную роль при изучении свойств любой кривой линии. В случае циклоиды обнаруживается любопытный факт: огибающей нормалей циклоиды служит точно такая же циклоида, только сдвинутая на 2а вниз и на πа вправо. Этот факт характерен именно для циклоиды.
4. Геометрическое определение циклоиды
Теперь мы дадим определение циклоиды как геометрического места точек, не пользуясь механикой. Проще всего поступить так. Рассмотрим произвольную прямую АВ (будем условно считать ее направление горизонтальным) и на ней точку М0. Далее рассмотрим всевозможные круги определенного радиуса, касающиеся этой прямой и расположенные по одну сторону от нее. На каждом круге от точки Т касания его с прямой АВ отложим (в направлении к точке М0) дугу ТМ, по длине равную отрезку М0Т. Геометрическое место точек М (взятых на всех упомянутых нами кругах) и будет циклоидой.
Установим еще одно важное свойство циклоиды и попробуем именно его положить в основу изучения этой кривой.
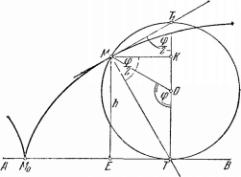
Рассмотрим треугольник МТТ1 (рис. 21), образованный вертикальным диаметром производящего круга, касательной к циклоиде и нормалью к ней.
Связь между «высотой» и наклоном касательной
Угол МТ1Т, как вписанный в окружность, равен половине центрального угла, опирающегося на ту же дугу, т. е. равен 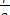
Обратим внимание на угол КМТ. Он равен углу МТ1Т. Из треугольника ТМТ1 получаем:
МТ = 2а sin
а из треугольника ТКМ:
КТ = МТ sin-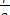
Сопоставляя эти результаты и замечая, что КТ = h, получим окончательно:
h = 2a sin 2
Мы выразили высоту точки М через угол между касательной в точке М и вертикалью (горизонталью мы по-прежнему считаем направление прямой АВ). Теперь выразим синус этого угла через «высоту». Получим, очевидно:
где через k обозначена постоянная для данной циклоиды величина 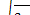
Теорема 4. Синус угла между касательной к циклоиде в точке М и вертикалью пропорционален корню квадратному из «высоты» точки М.
Этим свойством обладает, очевидно, любая циклоида. Возникает вопрос: в какой мере это свойство характеризует именно циклоиду: будет ли всякая кривая, обладающая этим свойством, непременно циклоидой? Можно доказать, что это будет именно так, — что верна и следующая (обратная) теорема:
Теорема 5. Если даны прямая АВ и точка М, то единственной кривой, удовлетворяющей условиям теоремы 4 и проходящей через точку М, будет циклоида.
При этом радиус производящего круга этой циклоиды связан с коэффициентом k, о котором говорится в теореме 4, следующим соотношением:
(Разумеется, расстояние точки М от АВ должно быть меньше, чем 2а.)
Строгое доказательство этой теоремы средствами элементарной математики очень громоздко, и мы его приводить здесь не будем.
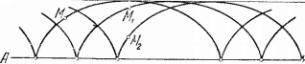
Если в условии теоремы 5 не оговорить, что искомая кривая проходит через наперед указанную точку М, то получится не одна, а бесконечное множество циклоид, которые получаются друг из друга параллельным сдвигом по направлению прямой АВ (одна из них проходит через точку М, другая — через М1 третья — через М2 и т. д.). Это множество, или, как его называют, семейство циклоид изображено на рис. 22.
Уравнения кривых. Циклоида.
Циклоида (от греческого — круглый). – кривая которую формирует фиксированная точка окружности радиуса r, катящейся без скольжения по неподвижной прямой. Термин «циклоида» предложил Г. Галилей.
Точки, в которых циклоида пересекается с прямой, по которой катится окружность (эту окружность обозначают как производящую, а прямую, по которой она катится, – направляющую), обозначают как точки возврата, а самые высокие точки на циклоиде, размещенные посредине между соседними точками возврата, именуют вершинами циклоиды,
Обозначим горизонтальную ось координат как прямую, по которой катится формирующая окружность радиуса r. Тогда имеем нижеследующие уравнения в прямоугольной системе координат:
.
Циклоида характеризуется параметрическими уравнениями:
Циклоиду можно получить в результате решения дифференциального уравнения:
Составить уравнения нормали к циклоиде
ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
Пусть имеем функцию y=f(x), где x – независимая переменная. Тогда дифференциал этой функции dy=f‘(x)dx также зависит от переменной x, причем от x зависит только первый сомножитель f‘(x) , а dx = Δx от x не зависит (приращение в данной точке x можно выбирать независимо от этой точки). Рассматривая dy как функцию x, мы можем найти дифференциал этой функции.
Дифференциал от дифференциала данной функции y=f(x) называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d 2 y: d(dy)=d 2 y.
Найдем выражение второго дифференциала. Т.к. dx от x не зависит, то при нахождении производной его можно считать постоянным, поэтому
Аналогично третьим дифференциалом или дифференциалом третьего порядка функции называется дифференциал от ее второго дифференциала:
Вообще дифференциалом n-го порядка называется первый дифференциал от дифференциала (n – 1)-го порядка: d n (y)=d(d n-1 y)
| d n y = f (n) (x)dx n |
Отсюда, пользуясь дифференциалами различных порядков, производную любого порядка можно представить как отношение дифференциалов соответствующего порядка:
ПРОИЗВОДНАЯ НЕЯВНОЙ ФУНКЦИИ
Пусть значения двух переменных x и y связаны между собой некоторым уравнением, которое символически запишем так:
| F(x, y) = 0. | (1) |
Если на некотором множестве D каждому значению переменной x соответствует единственное значение y, которое вместе с x удовлетворяет уравнению (1), то будем говорить, что это уравнение задает неявную функцию y=f(x).
Из определения следует, что для любой неявной функции y=f(x), заданной уравнением (1), имеет место тождество F(x, f(x)) ≡ 0, справедливое при всех x Î D.
Например, уравнение x 2 + y 2 – a 2 = 0 неявно определяет две элементарные функции 
Однако, не всякую неявно заданную функцию можно представить явно, т.е. в виде y=f(x).
Например, функции, заданные уравнениями y 2 – y – x 2 =0 или 
Заметим, что каждая явная функция y=f(x) может быть представлена и как неявная y–f(x) = 0.
Таким образом, неявная функция – это определенный способ задания зависимости между переменными x и y.
Рассмотрим правило нахождения производной неявной функции, не преобразовывая ее в явную, т.е. не представляя в виде y=f(x).
Чтобы найти производную у‘ неявной функции F(x, y)=0, нужно обе части этого уравнения продифференцировать по x, рассматривая у как функцию от x, и из этого полученного уравнения найти искомую производную y‘. Чтобы найти y», нужно уравнение F(x, y)=0 дважды продифференцировать по x и выразить y» и т.д.
Примеры. Найти производные функций заданных неявно.
Итак, производная неявной функции выражается, как правило, не только через аргумент, но и через функцию.
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ, ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ
Пусть даны два уравнения
| x=x(t),y=y(t), где t Î [T1, T2]. | (1) |
Каждому значению t из [T1, T2] соответствуют определенные значения x и y. Если рассматривать значения x и y как координаты точки на плоскости xOy, то каждому значению t будет соответствовать определенная точка плоскости. Когда t изменяется от T1 до T2, эта точка на плоскости описывает некоторую кривую. Уравнения (1) называются параметрическими уравнениями этой кривой, t называется параметром, а способ задания кривой уравнениями (1) называется параметрическим.
Предположим, что функция x=x(t) имеет обратную t=t(x). Тогда, очевидно, у является функцией от x: y=y[t(x)]. Следовательно, уравнения (1) определяют y как функцию от x, и говорят, что функция y от x задается параметрически.
При рассмотрении функций, заданных параметрически, исключение параметра не всегда возможно. Во многих случаях удобнее задавать различные значения t и затем вычислять соответствующие значения аргумента x и функции y.
Пример. Пусть кривая задана параметрическими уравнениями:
Построим эту кривую на плоскости, придавая различные значения параметру t и находя соответствующие значения х и у.
При t =0 M(R, 0).
Таким образом, получаем окружность с центром в начале координат, радиуса R. Здесь t обозначает угол, образованный радиусом, проведенным в некоторую точку окружности М(x, y), и осью Ox.
Если исключим из этих уравнений параметр t, то получим уравнение окружности, содержащее только x и y. Возводя в квадрат параметрические уравнения и складывая их, находим:
Выведем правило нахождения производных функций, заданных параметрически. Пусть x=x(t), y=y(t), причем на некотором отрезке [T1, T2] функции x(t) и y(t) дифференцируемы и x‘ ≠ 0.
Т.к. у – функция, зависящая от переменной x, то будем считать, что функция x=x(t) имеет обратную t=t(x).
Будем обозначать: yx‘ – производная функции по переменной x, yt‘, xt‘, tx‘ – соответственно производные по t и х.
Воспользовавшись правилом дифференцирования сложной функции, получим 

Окончательно, 
Полученную функцию 

Используя эту формулу, можно находить и производные высших порядков функций, заданных параметрически. Найдем 

 , y = arcsin (t–1). Найдем
, y = arcsin (t–1). Найдем  .
.Следовательно, 
Найти угловой коэффициент касательной к циклоиде x = a·(t – sin t), y = a·(1 – cost)
в произвольной точке (0 ≤t≤ 2·π).
Угловой коэффициент касательной 
x‘ = a·(1 – cost) ,y‘ = a·sin t. Поэтому 
Найти 
УРАВНЕНИЯ КАСАТЕЛЬНОЙ И НОРМАЛИ К КРИВОЙ
Рассмотрим кривую, уравнение которой есть y=f(x). Возьмем на этой кривой точку M(x0, y0), и составим уравнение касательной к данной кривой в точке M, предполагая, что эта касательная не параллельна оси Oy.
Уравнение прямой с угловым коэффициентом в общем виде есть у=kx + b. Поскольку для касательной k= f‘(x0), то получаем уравнение y= f‘(x0)·x + b. Параметр b найдем из условия, что касательная проходит через точку M(x0, y0). Поэтому ее координаты должны удовлетворять уравнению касательной: y0= f‘(x0)·x0 + b. Отсюда b=y0– f‘(x0)·x0.
| y = f ‘(x0)·(x – x0) + f(x0) |
Если касательная, проходящая через точку М(x0,y0) параллельна оси ординат (т.е. производная в этой точке не существует), то ее уравнение x= x0.
Наряду с касательной к кривой в данной точке часто приходится рассматривать нормаль.
Нормалью к кривой в данной точке называется прямая, проходящая через эту точку перпендикулярно к касательной в данной точке.
Из определения нормали следует, что ее угловой коэффициент kn связан с угловым коэффициентом касательной k равенством:

Учитывая, что нормаль также как и касательная проходит через точку M(x0, y0), то уравнение нормали к кривой y= f(x) в данной точке M имеет вид:
Ясно, что если касательная параллельна оси Ox, т.е.f‘(x0) = 0 и ее уравнение имеет вид y= y0, то нормаль в этой же точке будет перпендикулярна оси Ox. Значит, ее уравнение имеет вид x= x0.
- Составить уравнения касательной и нормали к графику функции у = tg 2 x в точке с абсциссой x0=π/4.
Уравнение касательной имеет вид y =4·(x – π/4) + 1 или y = 4x – π + 1.
Уравнение нормали будет y = –1/4·(x – π/4) + 1 или у = –1/4·x + π/16 + 1.
Составить уравнения касательной и нормали к графику функции у = 0.5·(x – 2) 2 + 5 в точке M(2; 5).
y‘= x – 2, y‘(2) = 0 . Следовательно, касательная параллельна оси Ox, а значит ее уравнение y= 5 . Тогда нормаль параллельна оси Oy и имеет уравнение x= 2 .
Найти уравнение касательной и нормали к эллипсу 
Найдем y‘ по правилу дифференцирования неявной функции 
Уравнение касательной: 

Уравнение нормали: 

Составить уравнения касательной и нормали к циклоиде x= t – sin t, y= 1 – cos tв точке М(x0; y0), которая соответствует значению параметра t = π/2.

Уравнение касательной: y = x – π/2 + 1 + 1, т.е. у = x – π/2 + 2.
Уравнение нормали: y = – x – π/2 – 1 + 1, т.е. у = – x – π/2.
ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
Теорема Ролля. Если функция y= f(x) непрерывна на отрезке [a; b], дифференцируема во всех внутренних точках этого отрезка (т.е. на (а; b)) и на концах отрезка обращается в нуль f(a) = f(b) = 0, то на (a; b) найдется хотя бы одна точка c Î (a; b), в которой f‘(c) = 0.
Доказательство. Так как функция f(x) непрерывна на [a; b], то по одной из теорем о непрерывных функциях она достигает на этом отрезке наибольшего значения и наименьшего. Пусть
Заметим, что если М = m, то f(x) = const = 0 (по условию теоремы f(a)=f(b)=0) и, следовательно, f‘(x)=0при всех x Î [a; b] .
Предположим, что M≠m, тогда, по крайней мере, одно из этих чисел отлично от нуля. Для определенности будем считать, что М ≠0 и М > 0.
Пусть в точке x = c f(c)=М, при этом c≠a и с ≠ b, т.к. f(a)=f(b)=0. Придадим значению c приращение Δx и рассмотрим новую точку c+Δx. Поскольку f(c) – наибольшее значение функции, то f(c+Δx) – f(c)≤0 для любого Δx. Отсюда следует, что
Переходя в этих неравенствах к пределу при Δx→0 и учитывая, что производная при x = c существует, будем иметь:
Но неравенства f‘(c) ≤ 0 и f‘(c) ≥ 0 одновременно возможны лишь в случае, когда
Эта теорема имеет простой геометрический смысл. Если непрерывная кривая, имеющая в каждой точке касательную, пересекает ось Ox в точках x=a и x=b, то на этой кривой найдется хотя бы одна точка с абсциссой c, a Î (a; b), что F‘(c)=0. Но F ‘(x) = f‘(x) – k, а значит,F‘(c) = f‘(c) – k = 0.
Подставляя в это равенство значение k, получим

что и требовалось доказать.
Теорему Лагранжа геометрически можно пояснить так. Рассмотрим график функции y=f(x), удовлетворяющий условиям теоремы и соединим концы графика на [a; b] хордой AB. Как мы уже отметили, отношение 
Теорема Коши. Если f(x) и g(x) – две функции, непрерывные на [a; b] и дифференцируемые внутри него, причем g‘(x) ≠ 0 при всех x Î (a; b), то внутри отрезка [a; b] найдется хотя бы одна точка c Î (a; b), что 
Доказательство.Определим число 
Составим вспомогательную функцию.
Несложно заметить, что F(a)=F(b)=0. Функция F(x) удовлетворяет на [a;b] всем условиям теоремы Ролля. Следовательно, найдется число сÎ(a; b) такое, что F‘(c) = 0. Но
откуда
Заметим, что теорему Коши нельзя 

http://www.calc.ru/Uravneniya-Krivykh-Tsikloida.html
http://toehelp.ru/theory/math/lecture07/lecture07.html