Интегрирование дифференциального уравнения изогнутой оси балки при двух участках.

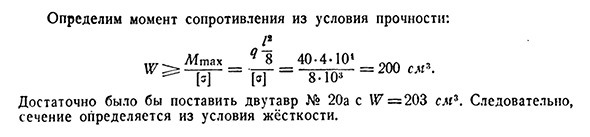
Интегрирование дифференциального уравнения изогнутой оси балки при двух участках.

• Интеграл дифференциальных уравнений криволинейной оси балки на двух участках. Если изгибающий момент в разных частях балки представлен разными формулами, то необходимо составить такое же количество дифференциальных уравнений, как и площадь на балке. Нагружают силой р на расстоянии от левой балки на двух опорах

в пролете Z, b от правой кромки b; пусть a » >B(рис. 287). Поддерживающий отклик луча равен H A=0, B=^ -. Возьмите начало координат левой опоры и правую ось X. Изгибающий момент в первом и втором сечениях выражается различными уравнениями^поэтому мы можем найти два произвольных сечения в абсциссах x^и x%. Значения y, M, C, D и абсциссы раздела

уравнения отмечены в индексе 1 первого раздела и индексе 2 второго. При Людмила Фирмаль

составлении моментального представления обеих секций рассмотрим левую часть балки, а затем первую секцию: l R Ml=LX1=Y Xi, для второй секции (секция O2): R М=А% — Р(х2-а)= — х — р(х2-а). Интегрирование термов вида P (x2-a) осуществляется без скобок, как это сделано в Примере 74. При этих условиях вычисление выглядит следующим образом: П Е Р В ы й Г А С Т О К Т О Р У ч а с Т О К А Д=M1=Dx1; EJy= — (18.31) Ежи’и=L42=DH2-Р(х2-а); ежи и=-Р(х2-а); с т Pbxl +(18.33) 4-C2×2 4-D2. (18.34) выражение для отклонения и вращения включает Интеграл четырех констант. Чтобы определить эти константы, нужно

написать четыре уравнения. Эти уравнения, как и в предыдущем случае, что-то знают о прогибе и угле поворота, всегда можно сделать, рассматривая сечение пучка таким сечением вещества является: Участок с, расположенный на границе двух участков, можно отнести как к первому, так и ко второму из них. Итак, величину прогиба и угла поворота сечения С можно вычислить как по формуле первого сечения, так и по формуле второго: то есть x1=x2=a; Если значение получено и B1=9a или y и 0, то оно должно быть одинаковым. Ежи=Ежи Альф () е дя^^е дя^. (b)§ 112]уравнение

криволинейной оси балки в двух сечениях 363 Таким образом, точки деления графика всегда дают два уравнения. Сечение A при x t=0 отклонение YG=O, ©> «B«x=I>y2=0. Подставляя выражения (18.31) и (18.33) вместо X>и уравнивая значение и правильную часть X% a, получаем условие (a): P A2|p_ _ R a * g>(A

°) 8 I2-I2P2 Откуда (18.35)) Аналогично она получается по условиям из формул (18.32) и (18.34 (&): 7• + ЦРУ+°я=7^ — П(°Б-«Б» Б Д Откуда Di=D(18.36) следовательно, константы интегрирования для обоих участков были одинаковыми. Это связано с принятием метода композиции и интегрирования

дифференциальных уравнений. Когда Формула (18.32) применяется к эталонному участку D, она получается на основе © Oh=09, следовательно, O9=0. Применение той же формулы (18.34) к ссылочному разделу B дает результаты, основанные на (d Здесь уравнения для y и 6 принимают следующий вид: 364 аналитические методы определения деформации[глава XV. Рассмотрим значение максимального прогиба f. это будет сечение с 0=0. Из формулы для 0! Мы видим это для X1=0., РА’ЗЕЛ площадь поперечного сечения В=а (И — #); Так как B O. Таким образом, 0t

между точкой А и точкой с меняет знак, то есть проходит через ноль. Людмила Фирмаль

Значит, наибольший прогиб будет у первого участка. Чтобы найти абсциссу xj соответствующего сечения, подставим это значение xj в выражение 0A и сделаем его равным нулю: — -^ -(/2 — £2) | = 0; таким образом, xj=1 — • Поэтому при перемещении от середины пролета к опоре Фигура. Центральный прогиб пролета 287 Два. В этом легко убедиться, подсчитав небольшую разницу между Если вы присваиваете выражению Y lf, RZ (R-B) / z (R-B*)RRU’Z l /

((18 37) 27EJZ-21EJ V\Z2/’ Расстояние участка с наибольшим отклонением

от левой опоры изменяется с изменением положения груза. Если сила P находится в середине пролета、 /. £Р/5 −2’Max-4 8£/, (18.38) Если переместить силу P на правую опору и установить предельное расстояние b равным нулю, то#->0; x0=—=x= = 0,577/. Tplt/ Из точек D и B (рис. 288) абсцисса точки с наибольшим отклонением изменяется только между 0,5/и 0,577 / между точками D и R. особенно при размещении Фигура. 288. (18.39) Число /Ш В Я/^.§ 1 1 2] формула для криволинейной оси балки на двух участках 3 6 5 П р и М Е Р 77.

Подобрать сечение стальной двутавровой балки с непрерывной нагрузкой q=4 т/м на полпролета(рис. 289), если пусковое напряжение[а]=1000кг/см2, а допустимое отклонение не должно превышать-jOOQ-пролет равен/=2,0 м. Давайте положим начало координат в точке I, ось x находится справа, а ось y-вверху. Нумерация участков показана на рисунке. Мы составляем и интегрируем дифференциальные уравнения криволинейных осей, считая

x на обоих участках от точки A. fl- Два. Фигура. Двести восемьдесят девять ЭДЖ ЭДЖ d2y * ДХ% Т О Р О й=м2, у ч а с т о с д Х2″2\2 2)’ EJys— — ^4″ —— 2^> ^2* Один. Два. Интегральная константа определяется из условия: x3= / » x » должно быть 2 = / >» ^8 = 0. х t=хз я Два» >> акстись Д х s’ >X i=X s I −2 >Эжит=Эжит. Дайте первые два условия: с 2_|?/ 8р-7?/ 4-7?/ 4 * ■48 ′ 16-24-384 * Из третьего и четвертого условий: Ди = ДС = 7?/ 4 Триста восемьдесят четыре Запишите уравнение прогиба первой секции в последней форме, так как максимальное прогибание будет иметь конец балки. Y ’

[+48 ′ 384J-384EJ L8I+G Максимальное отклонение (x=0)/= — Iql * WAEJ * Теперь мы можем

определить J: / _ из жестких условий. 7^ — 3 8 4£7′ Iql 7.40-8- 10E-103 384.2-10° 7= = 2910см. I балка № 24 момент инерции 7=3460см\366 метод анализа для определения деформации[гл. XVIII Определите момент сопротивления из условий интенсивности: Afmax8″ — — — Т Т-8-10″ — * * * см>’ I луч No. It достаточно разместить 20A С W=203cm*. Таким образом, поперечное сечение определяется из условий жесткости.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Изогнутая ось балки

Изогнутая ось балки

Изгиб балки сопровождается искривлением ее оси. При этом точки оси получают поперечные перемещения или прогибы, а поперечные сечения поворачиваются относительно своих нейтральных осей. Углы поворота поперечных сечений принимаются равными углам наклона j касательной к изогнутой оси балки. Прогибы и углы поворота в балках часто называются линейными и угловыми перемещениями.

— закон изменения прогиба оси балки;

АМВ – изогнутая ось (упругая линия) – кривая, в которую превращается прямолинейная до деформации ось балки после приложения нагрузки;

— угол наклона касательной.

Прогибы и углы поворота в балках являются переменными величинами, т. е. функциями координаты х.

О знаке :

j — положительно, если при совмещении оси балки с касательной идет движение по часовой стрелке.

На часть конструкций часто накладываются жесткие ограничения на перемещения, например для балочных мостов, кран-балок и т. д., т. е. возникает необходимость рассмотрения геометрической стороны задачи при изгибе.

I . Дифференциальное уравнение изогнутой оси балки

Вид ИОБ определяется

1. действием нагрузки, которая вызывает внутренние усилия M , Q , N ;

2. геометрической характеристикой I ;

Значит

I – момент инерции поперечного сечения балки относительно его нейтральной оси;

Е – модуль упругости материала балки.

, E , I – от x не зависят.

В лекции «Напряжения в случае плоского поперечного изгиба балки» (прошлый семестр) рассматривалось «Определение нормальных напряжений». При этом было рассмотрено 3 стороны задачи:

1. геометрическая сторона задачи;

2. физическая сторона задачи;

3. статическая сторона задачи.

При рассмотрении геометрической стороны задачи была установлена зависимость

, где

— относительная деформация;

— прогиб оси балки;

— радиус кривизны ИОБ.

При рассмотрении физической стороны задачи была использована гипотеза о том, что продольные волокна балки не давят друг на друга, т. е. что изгиб сводится к деформациям продольных волокон, которые деформируются изолированно, испытывая простое одноосное растяжение (сжатие). Эта гипотеза делает возможным для связи деформаций и напряжений при изгибе использование закона Гука.

В статической стороне задачи было рассмотрено следующее сечение

Суммарное действие внутренних напряжений должно быть равно внешним воздействиям.

Имеет место 2 условия равновесия:

1.

2.

— сила по элементарным площадкам;

— сила по всему сечению.

Отсюда (1),

— радиус кривизны ИОБ;

— жесткость балки при изгибе (изгибная жесткость).

Так как в выражение (1) вошли все 3 фактора M , E , I , то осталось выразить через y .

Для этого воспользуемся выражением из высшей математики

(2)

Приравниваем (1) и (2).

(3) точное дифференц. уравнение ИОБ

Так как в реальных конструкциях нормами проектирования допускаются сравнительно малые прогибы, а именно

, то ИОБ в реальности пологая.

Угол

Поскольку , а , то этим слагаемым в выражении (3) можно пренебречь.

(4)

Эта формула устанавливает зависимость между ,и 2-ой производной от прогиба.

Известно, что , когда момент, растягивая нижние волокна, обращает балку выпуклостью вниз.

Тогда из математики (вторая производная от функции отрицательна, если кривая обращена выпуклостью в положительную сторону оси y ).

Таким образом, при положительном изгибающем моменте, 2-ая производная должна быть отрицательной, следовательно в уравнении (4) удерживается знак «-» и формула имеет вид

(5) приближенное дифференц. уравнение ИОБ

Основные дифференциальные зависимости

Ранее известные зависимости:

(6)

,

(7)

Уравнения (7) позволяют, имея q , Q и M (а эти величины всегда возможно определить, построив эпюры в балках), получить значения y (прогиба) и j (угла поворота).

II . Методы решения дифференциальных уравнений ИОБ

Существует 3 метода решения дифференциальных уравнений ИОБ:

1. Метод непосредственного интегрирования

2. Метод начальных параметров

1. Метод непосредственного интегрирования

Метод непосредственного интегрирования заключается в непосредственном интегрировании уравнения (5).

(8)

Зная закон изменения можно определить y как функцию от x ().

Интегрирование ведется по участкам, для которых должны быть известны аналитические выражения изгибающих моментов .

В результате двукратного интегрирования на каждом участке появляются 2 произвольные постоянные С1 и С2.

Если балка разбивается на n участков, то постоянных интегрирования будет 2 × n .

Их определяют из

1. граничных условий (способов закрепления);

2. условий сопряжения участков.

1. Условия закрепления (граничные условия)

1) жесткое защемление

При Þ и

2) шарнирное опирание

При Þ и

При Þ и

Таким образом, с учетом граничных условий осталось неизвестных.

2. Условия сопряжения граничных участков

при Þ ,

Таким образом, всегда можно составить условия сопряжения и найти уравнение ИОБ.

Дифференциальное уравнение упругой линии балки и его интегрирование

При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом нормальными к изогнутой продольной оси (рис. 8.22). Деформированная (изогнутая) продольная ось балки называется упругой линией , а поступательные перемещения сечений, равные перемещениям y = y ( x ) их центров тяжести сечений – прогибами балки .

Между прогибами y ( x ) и углами поворота сечений θ ( x ) существует определенная зависимость. Из рис. 8.22 видно, что угол поворота сечения θ равен углу φ наклона касательной к упругой линии ( θ и φ — углы с взаимноперпендикулярными сторонами). Но согласно геометрическому смыслу первой производной y / = tg θ . Следовательно, tg θ = tg φ = y / .

В пределах упругих деформаций прогибы балок обычно значительно меньше высоты сечения h , а углы поворота θ не превышают 0.1 – 0.15 рад. В этом случае связь между прогибами и углами поворота упрощается и принимает вид θ = y / .

Определим теперь форму упругой линии. Влияние перерезывающих сил Q на прогибы балок, как правило, незначительно. Поэтому с достаточной точностью можно принять, что при поперечном изгибе кривизна упругой линии зависит только от величины изгибающего момента M z и жесткости EI z (см. уравнение (8.8)):

.

В то же время в неподвижной системе координат кривизна упругой линии, как и всякой плоской кривой,

.

Приравнивая правые части (8.26) и (8.27) и учитывая, что правила знаков для M z и y // были приняты независимо друг от друга, получаем

.

Это равенство называется дифференциальным уравнением упругой линии . При малых деформациях второе слагаемое в знаменателе мало по сравнению с единицей (при θ = 0.1 рад ( y / ) 2 =0.01 ) и им можно пренебречь. В результате получим приближенное дифференциальное уравнение упругой линии балки

.

Выбор знака в правой части (8.29) определяется направлением координатной оси y , так как от этого направления зависит знак второй производной y // . Если ось направлена вверх, то, как видно из рис. 8.23, знаки y // и M z совпадают, и в правой части надо оставить знак плюс. Если же ось направлена вниз, то знаки y // и M z противоположны, и это заставляет выбрать в правой части знак минус.

Заметим, что уравнение (8.29) справедливо только в пределах применимости закона Гука и лишь в тех случаях, когда плоскость действия изгибающего момента M z содержит одну из главных осей инерции сечения.

Интегрируя (8.29), находим сначала углы поворота сечений

,

а после второго интегрирования – прогибы балки

.

Постоянные интегрирования определяются из граничных условий. На участках с различными аналитическими выражениями для изгибающих моментов дифференциальные уравнения упругой линии также различны. Интегрирование этих уравнений при n участках дает 2 n произвольных постоянных. Для их определения к граничным условиям на опорах добавляются условия равенства прогибов и углов поворота на стыке двух смежных участков балки.