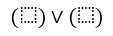Таблица истинности
Инструкция . При вводе с клавиатуры используйте следующие обозначения:
| Клавиша | Оператор | |
|---|---|---|
| ! | ¬ | Отрицание (НЕ) |
| | | | | Штрих Шеффера (И-НЕ) |
| # | ↓ | Стрелка Пирса (ИЛИ-НЕ) |
| * | & | Конъюнкция (И) |
| + | v | Дизъюнкция (ИЛИ) |
| ^ | ⊕ | Исключающее ИЛИ, сумма по модулю 2 (XOR) |
| @ | → | Импликация (ЕСЛИ-ТО) |
| % | ← | Обратная импликация |
| = | ≡ ( |
, ↔)
bc необходимо ввести так: a*b*c+a*b=c+a=b*c
Для ввода данных в виде логической схемы используйте этот сервис.
Для булевой функции, заданной вектором значений (например, 00111011 ) используйте ввод данных через таблицу.
Правила ввода логической функции
- Вместо символа v (дизъюнкция, ИЛИ) используйте знак + .
- Перед логической функцией не надо указывать обозначение функции. Например, вместо F(x,y)=(x|y)=(x^y) необходимо ввести просто (x|y)=(x^y) .
- Максимальное количество переменных равно 10 .
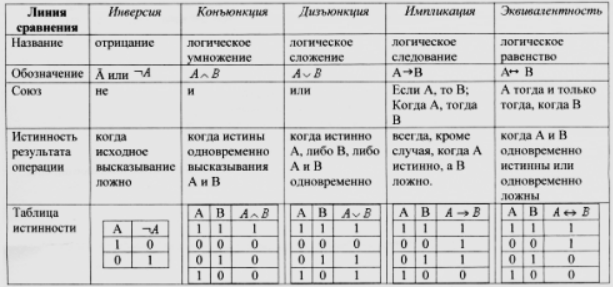
Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении. Если число высказываний в логическом выражении N, то таблица истинности будет содержать 2 N строк, так как существует 2 N различных комбинаций возможных значений аргументов.
Построение таблиц истинности
Вы будете перенаправлены на Автор24
Логическая функция – функция, переменные которой принимают одно из двух значений: $1$ или $0$.
Любую логическую функцию можно задать с помощью таблицы истинности: набор всех возможных аргументов записывается в левой части таблицы, а соответствующие значения логической функции – в правой части.
Таблица истинности – таблица, которая показывает, какие значения примет составное выражение при всех возможных наборах значений простых выражений, входящих в него.
Равносильными называются логические выражения, последние столбцы таблиц истинности которых совпадают. Равносильность обозначается с помощью знака $«=»$.
При составлении таблицы истинности важно учитывать следующий порядок выполнения логических операций:
Приоритетом в выполнении порядка выполнения операций пользуются скобки.
Алгоритм построения таблицы истинности логической функции
Определяют количество строк: кол-во строк = $2^n + 1$ (для строки заголовка), $n$ – количество простых выражений. Например, для функций двух переменных существует $2^2 = 4$ комбинации наборов значений переменных, для функций трех переменных – $2^3 = 8$ и т.д.
Определяют количество столбцов: кол-во столбцов = кол-во переменных + кол-во логических операций. При определении количества логических операций учитывают также порядок их выполнения.
Заполняют столбцы результатами выполнения логических операций в определенной последовательности, учитывая таблицы истинности основных логических операций.
Готовые работы на аналогичную тему
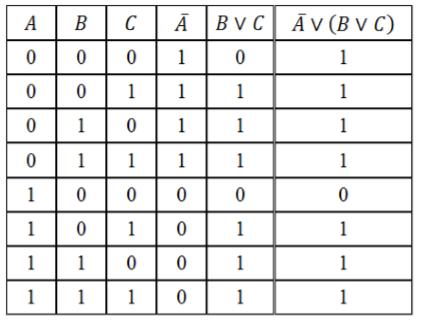
Составить таблицу истинности логического выражения $D=\bar \vee (B \vee C)$.
Решение:
Определим количество строк:
Количество простых выражений – $n=3$, значит
кол-во строк = $2^3 + 1=9$.
Определим количество столбцов:
Количество переменных – $3$.
Количество логических операций и их последовательность:
Кол-во столбцов = $3 + 3=6$.
Заполним таблицу, учитывая таблицы истинности логических операций.
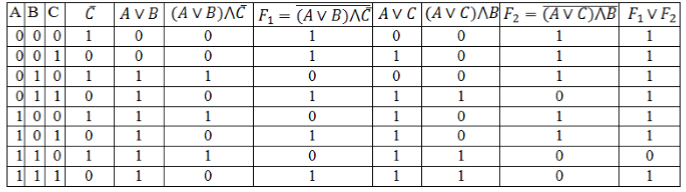
По данному логическому выражению построить таблицу истинности:
Решение:
Определим количество строк:
Количество простых выражений – $n=3$, значит
кол-во строк = $2^3 + 1=9$.
Определим количество столбцов:
Количество переменных – $3$.
Количество логических операций и их последовательность:
- отрицание ($\bar
$); - дизъюнкция, т.к. она находится в скобках ($A \vee B$);
- конъюнкция ($(A\vee B)\bigwedge \overline
$); - отрицание, которое обозначим $F_1$ ($\overline<(A\vee B)\bigwedge \overline
>$); - дизъюнкция ($A \vee C$);
- конъюнкция ($(A\vee C)\bigwedge B$);
- отрицание, которое обозначим $F_2$ ($\overline<(A\vee C)\bigwedge B>$);
Кол-во столбцов = $3 + 8 = 11$.
Заполним таблицу, учитывая таблицу истинности логических операций.
Алгоритм построения логической функции по ее таблице истинности
- Выделяют в таблице истинности строки со значением функции, равным $1$.
- Выписывают искомую формулу как дизъюнкцию нескольких логических выражений. Количество этих выражений равно количеству выделенных строк.
- Каждое логическое выражение в этой дизъюнкции записать как конъюнкцию аргументов функции.
- В случае, когда значение какого-то из аргументов функции в соответствующей строке таблицы принимает значение $0$, то этот аргумент записать в виде его отрицания.
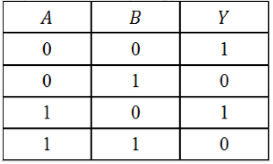
По данной таблице истинности некоторой логической функции $Y(A,B)$ cоставить соответствующую логическую функцию.
Решение:
- Значение функции равно $1$ в $1$-й и $3$-й строках таблицы.
- Поскольку имеем $2$ строки, получим дизъюнкцию двух элементов:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата написания статьи: 12 04 2016
Построение таблицы истинности. СДНФ. СКНФ. Полином Жегалкина.
Онлайн калькулятор позволяет быстро строить таблицу истинности для произвольной булевой функции или её вектора, рассчитывать совершенную дизъюнктивную и совершенную конъюнктивную нормальные формы, находить представление функции в виде полинома Жегалкина, строить карту Карно и классифицировать функцию по классам Поста.
Калькулятор таблицы истинности, СКНФ, СДНФ, полинома Жегалкина
введите функцию или её вектор
Построено таблиц, форм:
Как пользоваться калькулятором
- Введите в поле логическую функцию (например, x1 ∨ x2) или её вектор (например, 10110101)
- Укажите действия, которые необходимо выполнить с помощью переключателей
- Укажите, требуется ли вывод решения переключателем «С решением»
- Нажмите на кнопку «Построить»
Видеоинструкция к калькулятору
Используемые символы
В качестве переменных используются буквы латинского и русского алфавитов (большие и маленькие), а также цифры, написанные после буквы (индекс переменной). Таким образом, именами переменных будут: a , x , a1 , B , X , X1 , Y1 , A123 и так далее.
Для записи логических операций можно использовать как обычные символы клавиатуры ( * , + , ! , ^ , -> , = ), так и символы, устоявшиеся в литературе ( ∧ , ∨ , ¬ , ⊕ , → , ≡ ). Если на вашей клавиатуре отсутствует нужный символ операции, то используйте клавиатуру калькулятора (если она не видна, нажмите «Показать клавиатуру»), в которой доступны как все логические операции, так и набор наиболее часто используемых переменных.
Для смены порядка выполнения операций используются круглые скобки ().
Обозначения логических операций
- И (AND): & • ∧ *
- ИЛИ (OR): ∨ +
- НЕ (NOT): ¬ !
- Исключающее ИЛИ (XOR): ⊕ ^
- Импликация: -> → =>
- Эквивалентность: =
Что умеет калькулятор
- Строить таблицу истинности по функции
- Строить таблицу истинности по двоичному вектору
- Строить совершенную конъюнктивную нормальную форму (СКНФ)
- Строить совершенную дизъюнктивную нормальную форму (СДНФ)
- Строить полином Жегалкина (методами Паскаля, треугольника, неопределённых коэффициентов)
- Определять принадлежность функции к каждому из пяти классов Поста
- Строить карту Карно
- Минимизировать ДНФ и КНФ
- Искать фиктивные переменные
Что такое булева функция
Булева функция f(x1, x2, . xn) — это любая функция от n переменных x1, x2, . xn, в которой её аргументы принимают одно из двух значений: либо 0, либо 1, и сама функция принимает значения 0 или 1. То есть это правило, по которому произвольному набору нулей и единиц ставится в соответствие значение 0 или 1. Подробнее про булевы функции можно посмотреть на Википедии.
Что такое таблица истинности?
Таблица истинности — это таблица, описывающая логическую функцию, а именно отражающую все значения функции при всех возможных значениях её аргументов. Таблица состоит из n+1 столбцов и 2 n строк, где n — число используемых переменных. В первых n столбцах записываются всевозможные значения аргументов (переменных) функции, а в n+1-ом столбце записываются значения функции, которые она принимает на данном наборе аргументов.
Довольно часто встречается вариант таблицы, в которой число столбцов равно n + число используемых логических операций. В такой таблице также первые n столбцов заполнены наборами аргументов, а оставшиеся столбцы заполняются значениями подфункций, входящих в запись функции, что позволяет упростить расчёт конечного значения функции за счёт уже промежуточных вычислений.
Логические операции
Логическая операция — операция над высказываниями, позволяющая составлять новые высказывания путём соединения более простых. В качестве основных операций обычно называют конъюнкцию (∧ или &), дизъюнкцию (∨ или |), импликацию (→), отрицание (¬), эквивалентность (=), исключающее ИЛИ (⊕).
Таблица истинности логических операций
| a | b | a ∧ b | a ∨ b | ¬a | ¬b | a → b | a = b | a ⊕ b |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
Как задать логическую функцию
Есть множество способов задать булеву функцию:
- таблица истинности
- характеристические множества
- вектор значений
- матрица Грея
- формулы
Рассмотрим некоторые из них:
Чтобы задать функцию через вектор значений необходимо записать вектор из 2 n нулей и единиц, где n — число аргументов, от которых зависит функция. Например, функцию двух аргументов можно задать так: 0001 (операция И), 0111 (операция ИЛИ).
Чтобы задать функцию в виде формулы, необходимо записать математическое выражение, состоящее из аргументов функции и логических операций. Например, можно задать такую функцию: a∧b ∨ b∧c ∨ a∧c
Способы представления булевой функции
С помощью формул можно получать огромное количество разнообразных функций, причём с помощью разных формул можно получить одну и ту же функцию. Иногда бывает весьма полезно узнать, как построить ту или иную функцию, используя лишь небольшой набор заданных операций или используя как можно меньше произвольных операций. Рассмотрим основные способы задания булевых функций:
- Совершенная дизъюнктивная нормальная форма (СДНФ)
- Совершенная конъюнктивная нормальная форма (СКНФ)
- Алгебраическая нормальная форма (АНФ, полином Жегалкина)
Совершенная дизъюнктивная нормальная форма (ДНФ)
Простая конъюнкция — это конъюнкция некоторого конечного набора переменных, или их отрицаний, причём каждая переменная встречается не более одного раза.
Дизъюнктивная нормальная форма (ДНФ) — это дизъюнкция простых конъюнкций.
Совершенная дизъюнктивная нормальная форма (СДНФ) — ДНФ относительно некоторого заданного конечного набора переменных, в каждую конъюнкцию которой входят все переменные данного набора.
Например, ДНФ является функция ¬a bc ∨ ¬a ¬b c ∨ ac, но не является СДНФ, так как в последней конъюнкции отсутствует переменная b.
Совершенная конъюнктивная нормальная форма (КНФ)
Простая дизъюнкция — это дизъюнкция одной или нескольких переменных, или их отрицаний, причём каждая переменная входит в неё не более одного раза.
Конъюнктивная нормальная форма (КНФ) — это конъюнкция простых дизъюнкций.
Совершенная конъюнктивная нормальная форма (СКНФ) — КНФ относительно некоторого заданного конечного набора переменных, в каждую дизъюнкцию которой входят все переменные данного набора.
Например, КНФ является функция (a ∨ b) ∧ (a ∨ b ∨ c), но не является СДНФ, так как в первой дизъюнкции отсутствует переменная с.
Алгебраическая нормальная форма (АНФ, полином Жегалкина)
Алгебраическая нормальная форма, полином Жегалкина — это форма представления логической функции в виде полинома с коэффициентами вида 0 и 1, в котором в качестве произведения используется операция конъюнкции, а в качестве сложения — исключающее ИЛИ.
Примеры полиномов Жегалкина: 1, a, a⊕b, ab⊕a⊕b⊕1
Алгоритм построения СДНФ для булевой функции
- Построить таблицу истинности для функции
- Найти все наборы аргументов, на которых функция принимает значение 1
- Выписать простые конъюнкции для каждого из наборов по следующему правилу: если в наборе переменная принимает значение 0, то она входит в конъюнкцию с отрицанием, а иначе без отрицания
- Объединить все простые конъюнкции с помощью дизъюнкции
Алгоритм построения СКНФ для булевой функции
- Построить таблицу истинности для функции
- Найти все наборы аргументов, на которых функция принимает значение 0
- Выписать простые дизъюнкции для каждого из наборов по следующему правилу: если в наборе переменная принимает значение 1, то она входит в дизъюнкцию с отрицанием, а иначе без отрицания
- Объединить все простые дизъюнкции с помощью конъюнкции
Алгоритм построения полинома Жегалкина булевой функции
Есть несколько методов построения полинома Жегалкина, в данной статье рассмотрим наиболее удобный и простой из всех.
- Построить таблицу истинности для функции
- Добавить новый столбец к таблице истинности и записать в 1, 3, 5. ячейки значения из тех же строк предыдущего столбца таблицы истинности, а к значениям в строках 2, 4, 6. прибавить по модулю два значения из соответственно 1, 3, 5. строк.
- Добавить новый столбец к таблице истинности и переписать в новый столбец значения 1, 2, 5, 6, 9, 10. строк, а к 3, 4, 7, 8, 11, 12. строкам аналогично предыдущему пункту прибавить переписанные значения.
- Повторить действия каждый раз увеличивая в два раза количество переносимых и складываемых элементов до тех пор, пока длина не станет равна числу строк таблицы.
- Выписать булевы наборы, на которых значение последнего столбца равно единице
- Записать вместо единиц в наборах имена переменных, соответствующие набору (для нулевого набора записать единицу) и объединить их с помощью операции исключающего ИЛИ.
Примеры построения различных представлений логических функций
Построим совершенные дизъюнктивную и дизъюнктивную нормальные формы, а также полином Жегалкина для функции трёх переменных F = ¬a b∨ ¬b c∨ca
1. Построим таблицу истинности для функции
| a | b | c | ¬a | ¬a ∧b | ¬b | ¬b ∧c | ¬a ∧b∨ ¬b ∧c | c∧a | ¬a ∧b∨ ¬b ∧c∨c∧a |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
Построение совершенной дизъюнктивной нормальной формы:
Найдём наборы, на которых функция принимает истинное значение: < 0, 0, 1 > < 0, 1, 0 > < 0, 1, 1 > < 1, 0, 1 >
В соответствие найденным наборам поставим элементарные конъюнкции по всем переменным, причём если переменная в наборе принимает значение 0, то она будет записана с отрицанием:
Объединим конъюнкции с помощью дизъюнкции и получим совершенную дизъюнктивную нормальную форму:
Построение совершенной конъюнктивной нормальной формы:
Найдём наборы, на которых функция принимает ложное значение: < 0, 0, 0 > < 1, 0, 0 >
В соответствие найденным наборам поставим элементарные дизъюнкции по всем переменным, причём если переменная в наборе принимает значение 1, то она будет записана с отрицанием:
Объединим дизъюнкции с помощью конъюнкции и получим совершенную конъюнктивную нормальную форму:
Построение полинома Жегалкина:
Добавим новый столбец к таблице истинности и запишем в 1, 3, 5 и 7 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 2, 4, 6 и 8 сложим по модулю два со значениями из соответственно 1, 3, 5 и 7 строк:
| a | b | c | F | 1 | |
| 0 | 0 | 0 | 0 | → | 0 |
| 0 | 0 | 1 | 1 | ⊕ 0 | 1 |
| 0 | 1 | 0 | 1 | → | 1 |
| 0 | 1 | 1 | 1 | ⊕ 1 | 0 |
| 1 | 0 | 0 | 0 | → | 0 |
| 1 | 0 | 1 | 1 | ⊕ 0 | 1 |
| 1 | 1 | 0 | 0 | → | 0 |
| 1 | 1 | 1 | 1 | ⊕ 0 | 1 |
Добавим новый столбец к таблице истинности и запишем в 1 и 2, 5 и 6 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 3 и 4, 7 и 8 сложим по модулю два со значениями из соответственно 1 и 2, 5 и 6 строк:
| a | b | c | F | 1 | 2 | |
| 0 | 0 | 0 | 0 | 0 | → | 0 |
| 0 | 0 | 1 | 1 | 1 | → | 1 |
| 0 | 1 | 0 | 1 | 1 | ⊕ 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | ⊕ 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | → | 0 |
| 1 | 0 | 1 | 1 | 1 | → | 1 |
| 1 | 1 | 0 | 0 | 0 | ⊕ 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | ⊕ 1 | 0 |
Добавим новый столбец к таблице истинности и запишем в 1 2, 3 и 4 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 5, 6, 7 и 8 сложим по модулю два со значениями из соответственно 1, 2, 3 и 4 строк:
| a | b | c | F | 1 | 2 | 3 | |
| 0 | 0 | 0 | 0 | 0 | 0 | → | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | → | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | → | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | → | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | ⊕ 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 | ⊕ 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | ⊕ 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | ⊕ 1 | 1 |
Окончательно получим такую таблицу:
| a | b | c | F | 1 | 2 | 3 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 |
Выпишем наборы, на которых получившийся вектор принимает единичное значение и запишем вместо единиц в наборах имена переменных, соответствующие набору (для нулевого набора следует записать единицу):
Объединяя полученные конъюнкции с помощью операции исключающего или, получим полином Жегалкина: c⊕b⊕bc⊕ab⊕abc
Programforyou — это сообщество, в котором Вы можете подтянуть свои знания по программированию, узнать, как эффективно решать те или иные задачи, а также воспользоваться нашими онлайн сервисами.
http://spravochnick.ru/informatika/algebra_logiki_logika_kak_nauka/postroenie_tablic_istinnosti/
http://programforyou.ru/calculators/postroenie-tablitci-istinnosti-sknf-sdnf