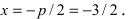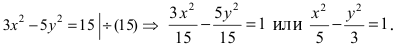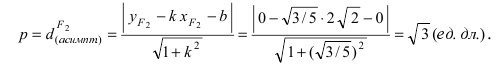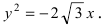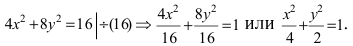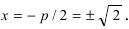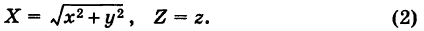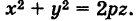Парабола
Элементы параболы
0F — фокальная ось
0 — вершина
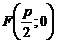
ε=1 — эксцентриситет
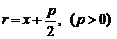
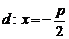
p — фокальный параметр
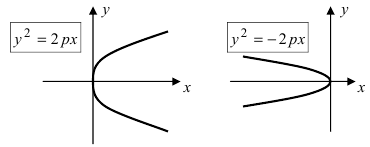
Каноническое уравнение параболы (ось Ox совпадает с фокальной осью, начало координат – с вершиной параболы): y 2 =2px
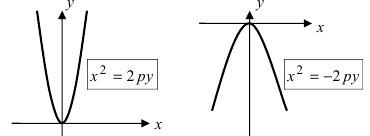
При p x 2 =2py
При p>0 ветви параболы направлены вверх, при p 2 /2+(y-1) 2 /2=1, необходимо набрать в поле x^2/2+(y-1)^2/2=1 и нажать кнопку График параболы .
Самостоятельно построить график можно, используя операцию выделения полного квадрата.
Задача 61746 Составить каноническое уравнение.
Условие
Составить каноническое уравнение параболы, если известно, что: а) парабола имеет фокус F (0, 2) и вершину в точке О (0, 0); б) парабола симметрична относительно оси абсцисс и проходит через точки О (0, 0) и М( 1, —4); в) парабола симметрична относительно оси ординат Оу и проходит через точки 0 (0, 0) и N(6, —2).
Решение
а) парабола имеет фокус F (0, 2) и вершину в точке О
О т в е т. x^2=2*4y
б) парабола симметрична относительно оси абсцисс и проходит через точку О (0, 0)
значит уравнение принимает вид:
парабола проходит через точy
М( 1, —4)
подставляем координаты точки в уравнение:
О т в е т. y^2=2*8x
в) парабола симметрична относительно оси ординат Оу и проходит через точку 0 (0, 0)
значит уравнение принимает вид:
парабола проходит через точy
N(6, —2).
Парабола — определение и вычисление с примерами решения
Парабола:
Определение: Параболой называется геометрическое место точек равноудаленных от выделенной точки F, называемой фокусом параболы, и прямой (l), называемой директрисой.
Получим каноническое уравнение параболы. Выберем декартову систему координат так, чтобы фокус F лежал на оси абсцисс, а директриса проходила бы через точку, расположенную симметрично фокусу, перпендикулярно к оси абсцисс (Рис. 34). Пусть точка M(х; у) принадлежит параболе: Вычислим расстояния от точки M(х; у) до фокуса и директрисы
Рис. 34. Парабола, (уравнение директрисы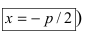
Возведем обе части уравнения в квадрат
Раскрывая разность квадратов, стоящую в правой части уравнения, получим каноническое уравнение параболы: 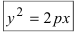
Рис. 35а. Параболы и их уравнения.
Рис. 356. Параболы и их уравнения.
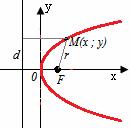
Найдем координаты точек пересечения параболы с координатными осями:
— точка пересечения параболы с осью абсцисс;
— точка пересечения параболы с осью ординат.
Определение: Точка О(0; 0) называется вершиной параболы.
Если точка М(х; у) принадлежит параболе, то ей принадлежат и точка 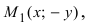
Пример:
Дано уравнение параболы 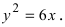
Решение:
Так как из уравнения параболы 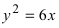
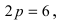
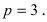
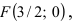
Пример:
Составить каноническое уравнение параболы, фокус которой лежит на оси Ох слева от начала координат, а параметр р равен расстоянию от фокуса гиперболы 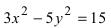
Решение:
Для определения координат фокусов гиперболы преобразуем её уравнение к каноническому виду.
Гипербола:
Следовательно, действительная полуось гиперболы 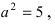
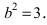
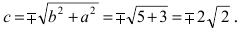
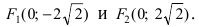
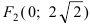
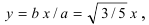
Следовательно, каноническое уравнение параболы, фокус которой лежит на оси Ох слева от начала координат имеет вид:
Пример:
Составить каноническое уравнение параболы, фокус которой совпадает с одним из фокусов эллипса 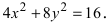
Решение:
Для определения координат фокусов эллипса преобразуем его уравнение к каноническому виду. Эллипс:
Следовательно, большая полуось эллипса 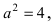
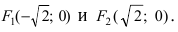
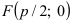
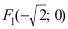
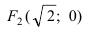

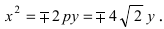
Уравнение параболоида вращения
Пусть вертикальная парабола
расположенная в плоскости Охz, вращается вокруг своей оси (ось Oz). При вращении получается поверхность, носящая название параболоида вращения (рис. 207).
Для вывода уравнения поверхности рассмотрим произвольную точку 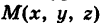
Так как точки М и N расположены в одной и той же горизонтальной плоскости и CN = СМ как радиусы одной и той же окружности, то имеем
Подставляя формулы (2) в уравнение (1), получим уравнение параболоида вращения
Заметим, что форму параболоида вращения имеет поверхность ртути, находящейся в вертикальном цилиндрическом сосуде, быстро вращающемся вокруг своей оси. Это обстоятельство используют в технике для получения параболических зеркал.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Многогранник
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Четырехугольник
- Многогранники
- Окружность
- Эллипс
- Гипербола
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://reshimvse.com/zadacha.php?id=61746
http://www.evkova.org/parabola
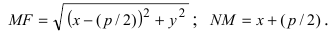
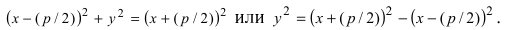
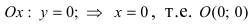 — точка пересечения параболы с осью абсцисс;
— точка пересечения параболы с осью абсцисс;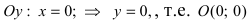 — точка пересечения параболы с осью ординат.
— точка пересечения параболы с осью ординат.