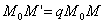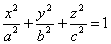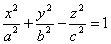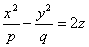Составьте параметрические уравнения кругового конуса

Параметрические уравнения наклонного кругового конуса

Я пытаюсь определить параметрические уравнения для конкретной формы наклонного кругового конуса без успеха. Исчерпывающие веб-поиски и многие тексты не были плодотворными в отношении параметризации косых круговых конусов. Поскольку я не знаю названия для формы конуса, я опишу его свойства. Для справки ориентация конуса с вершиной в точке (0, 0, 0) и открывается вдоль оси + z до высоты «h» с диаметром основания «b». Круговые сечения в плоскости xy ограничены тем, что $ 0 \ leq y \ leq b $ (т. Е. Значения y всегда положительны в квадрантах I и II плоскости xy) и $ — \ frac b2 \ leq x \ leq \ frac b2 $. Ось — это линия через точки (0, 0, 0) и (0, $ \ frac b2 $, h). Точка (0, 0) каждой окружности в плоскости x-y должна находиться в точке z, т. Е. (0, 0, z). Тогда форма конуса будет прямоугольным треугольником в 2D, когда вид с оси х с высотой конуса является вертикальной линией вдоль оси z, а самый длинный угол от (0, 0, 0) до (0, b, h). Грубое двумерное текстовое изображение желаемой формы конуса ниже с горизонтальной осью z (+ z влево) и y-axix vertical (+ y вниз). Может ли кто-нибудь помочь с параметризацией такого формованного конуса? Очевидно, что я не разработал неявное уравнение, хотя, по-видимому, оно должно быть просто вариацией вида $ x ^ 2 + y ^ 2 = z ^ 2 $. (Ориентация конуса, описанная здесь, предназначена только для простой справки, и в идеале параметризация должна работать в любой ориентации.) Спасибо!

Конус

Конус (от др.-греч. κώνος «сосновая шишка»),— поверхность, образованная в пространстве множеством лучей (образующих конуса), соединяющих все точки некоторой плоской кривой (направляющей конуса) с данной точкой пространства (вершиной конуса).

Если направляющая конуса — замкнутая кривая, то коническая поверхность служит границей пространственного тела, которое также называют конусом (см. рисунок), а внутренность этой кривой называют основанием конуса, Если основание конуса представляет собой многоугольник, такой конус является пирамидой.

Иногда вместо лучей рассматривают прямые, тогда получается двойной конус, состоящий из двух симметричных относительно вершины частей.

Конус и связанные с ним конические сечения играют большую роль в математике, астрономии и других науках.

Связанные определения

• Боковая поверхность конуса — объединение образующих конуса; образующая поверхность конуса является конической поверхностью.
• Высота конуса — отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка).
• Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
• Конусность — соотношение высоты и диаметра основания конуса.

Типы конусов

Прямой круговой конус

Прямой и косой круговые конусы с равным основанием и высотой: их объём одинаков

Усечённый прямой круговой конус

• Прямой конус — конус, основание которого имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром; при этом прямая, соединяющая вершину и центр основания, называется осью конуса.
• Косой (или наклонный) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
• Круговой конус — конус, основание которого является кругом.
• Конус вращения, или прямой круговой конус (часто под конусом подразумевают именно его) — конус, который можно получить вращением (то есть тело вращения) прямоугольного треугольника вокруг прямой, содержащей катет треугольника (эта прямая является осью конуса).
• Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом: последние два имеют бесконечный объём.
• Усечённый конус или конический слой — часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием.
• Равносторонний конус — конус вращения, образующая которого равна диаметру основания.

Свойства

• Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания.

V = 1 3 S H , SH,> где S — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.

• Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания.
• Телесный угол при вершине прямого кругового конуса равен

2 π ( 1 − cos ⁡ α 2 ) , ight),> где α — угол раствора конуса.

• Площадь боковой поверхности прямого кругового конуса равна

S = π R t , а в общем случае S = t l 2 , <2>>,> где R — радиус основания, t = R 2 + H 2 +H^<2>>>> — длина образующей, l — длина границы основания. Полная площадь поверхности (то есть сумма площадей боковой поверхности и основания) равна S = π R ( t + R ) , для прямого кругового конуса и S = t l 2 + S , <2>>+S,> для произвольного, где S — площадь основания.

• Объём кругового (не обязательно прямого) конуса равен

V = 1 3 π R 2 H . pi R^<2>H.>

• Для усечённого кругового конуса (не обязательно прямого) объём равен:

V = 1 3 π H ( R 2 + R r + r 2 ) , pi H(R^<2>+Rr+r^<2>),> где R и r — радиусы соответственно нижнего и верхнего оснований, H — высота от плоскости нижнего основания,до верхнего основания.

• Для произвольного усечённого конуса (не обязательно прямого и кругового) объём равен:

V = 1 3 ( H 2 S 2 − H 1 S 1 ) , (H_<2>S_<2>-H_<1>S_<1>),> где S 1 > и S 2 > — площади соответственно верхнего (ближнего к вершине) и нижнего оснований, H 1 > и H 2 > — расстояния от плоскости соответственно верхнего и нижнего основания до вершины.

• Пересечение плоскости с прямым круговым конусом является одним из конических сечений (в невырожденных случаях — эллипсом, параболой или гиперболой, в зависимости от положения секущей плоскости).

Уравнение прямого кругового конуса

Уравнения, задающие боковую поверхность прямого кругового конуса с углом раствора 2Θ, вершиной в начале координат и осью, совпадающей с осью Oz:

• В сферической системе координат с координатами (r, φ, θ):

θ = Θ .

• В цилиндрической системе координат с координатами (r, φ, z):

z = r ⋅ ctg ⁡ Θ Theta > или r = z ⋅ tg ⁡ Θ . Theta .>

• В декартовой системе координат с координатами (x, y, z):

z = ± x 2 + y 2 ⋅ ctg ⁡ Θ . +y^<2>>>cdot operatorname Theta .> Это уравнение в каноническом виде записывается как x 2 a 2 + y 2 a 2 − z 2 c 2 = 0 , >>>+>>>->>>=0,> где константы a, с определяются пропорцией c / a = cos ⁡ Θ / sin ⁡ Θ . Отсюда видно, что боковая поверхность прямого кругового конуса представляет собой поверхность второго порядка (она носит название коническая поверхность). В общем виде коническая поверхность второго порядка опирается на эллипс; в подходящей декартовой координатной системе (оси Ох и Оу параллельны осям эллипса, вершина конуса совпадает с началом координат, центр эллипса лежит на оси Oz) её уравнение имеет вид x 2 a 2 + y 2 b 2 − z 2 c 2 = 0 , >>>+>>>->>>=0,> причём a/c и b/c равны полуосям эллипса. В наиболее общем случае, когда конус опирается на произвольную плоскую поверхность, можно показать, что уравнение боковой поверхности конуса (с вершиной в начале координат) задаётся уравнением f ( x , y , z ) = 0 , где функция f ( x , y , z ) является однородной, то есть удовлетворяющей условию f ( α x , α y , α z ) = α n f ( x , y , z ) f(x,y,z)> для любого действительного числа α.

Развёртка

Прямой круговой конус как тело вращения образован прямоугольным треугольником, вращающимся вокруг одного из катетов, где h — высота конуса от центра основания до вершины — является катетом прямоугольного треугольника, вокруг которого происходит вращение. Второй катет прямоугольного треугольника r — радиус в основании конуса. Гипотенузой прямоугольного треугольника является l — образующая конуса.

В создании развёртки конуса могут использоваться всего две величины r и l. Радиус основания r определяет в развертке круг основания конуса, а сектор боковой поверхности конуса определяет образующая боковой поверхности l, являющаяся радиусом сектора боковой поверхности. Угол сектора φ в развёртке боковой поверхности конуса определяется по формуле:

Составьте параметрические уравнения кругового конуса

Глава 46. Поверхности второго порядка

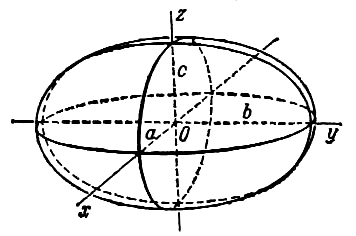
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

(1).

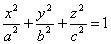
Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c — сжатым. В случае, когда a=b=c , эллипсоид представляет собой сферу.

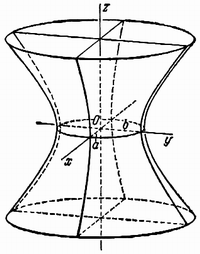
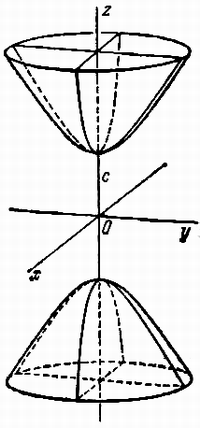
Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (2)

. (3)

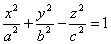
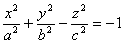
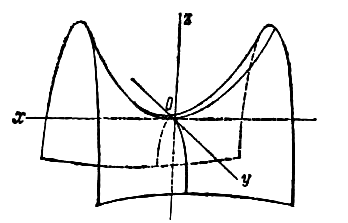
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), — двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b ) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.

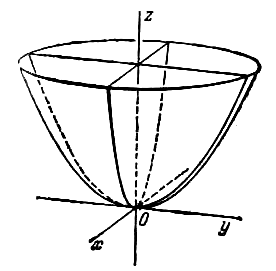
Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (4)

, (5)

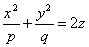
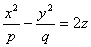
где p и q — положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), — гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q , параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).

Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).

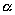
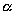
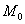
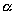
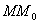
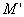
Выберем какую-нибудь плоскость; обозначим ее буквой . Зададим, кроме того, некоторое положительное число q . Пусть М — произвольная точка пространства, не лежащая на плоскости , — основание перпендикуляра, опущенного на плоскость из точки М. Переместим точку М по прямой в новое положение так, чтобы имело место равенство

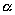
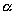
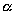
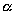
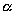
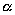
и чтобы после перемещения точка осталась с той же стороны от плоскости , где она была первоначально (рис. 6). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости ; точки, которые расположены на плоскости , оставим на своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости , переместятся; при этом расстояние от каждой точки до плоскости изменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас перемещение точек пространства называется его равномерным сжатием к плоскости ; число q носит название коэффициента сжатия.

Пусть дана некоторая поверхность F ; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F ’. Будем говорить, что поверхность F ’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).

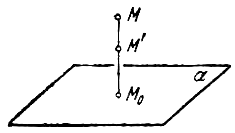
ПРИМЕР. Доказать, что произвольный трехосный эллипсоид

может быть получен из сферы

в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия и к плоскости Oxz с коэффициентом сжатия .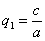

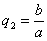
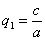
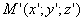
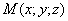
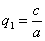
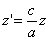
ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом и пусть — точка, в которую переходит при этом точка . Выразим координаты x’, y’, z ’ точки М’ через координаты x, y, z точки М. Так как прямая MM ’ перпендикулярна к плоскости Oxy , то x’=x, y’=y . С другой стороны, так как расстояние от точки М’ до плоскости Oxy равно расстоянию от точки М до этой плоскости, умноженному на число , то .

Таким образом, мы получаем искомые выражения:

, , (6)

, , (7)

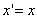
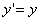
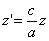
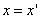
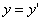
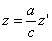
Предположим, что M(x; y; z ) — произвольная точка сферы

.

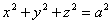
Заменим здесь x, y, z их выражениями (7); получим

,

.

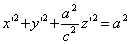
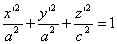
Следовательно, точка M’(x’; y’; z ’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам

, , ;

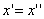
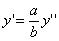
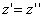
тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.

Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.

имеет две системы прямолинейных образующих, которые определяются уравнениями:

, ;

, ,

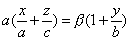
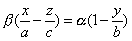
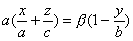
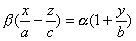
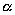
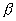
где и — некоторые числа, не равные одновременно нулю. Гиперболический параболоид

также имеет две системы прямолинейных образующих, которые определяются уравнениями

, ;

, .

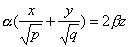
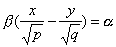
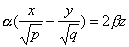
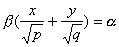
Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L . Точка S называется вершиной конуса; линия L — направляющей.

Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).