Задача 12615 1) Составить уравнение плоскости.
Условие
1) Составить уравнение плоскости, проходящей через начало координат перпендикулярно к векторы AB, если A(5,-2,3) B(1,-3,5)
2) Определить при каком значении B плоскости x-4y+z=0 и 2x+By+10z=0 будут перпендикулярны
Решение
1) Уравнение плоскости, проходящей через начало координат, имеет вид
ax+by+cz=0
Нормальный вектор этой плоскости имеет координаты
vector
Вектор АВ имеет координаты (1-5;-3-(-2);5-3)=(-4;-1;2).
По условию вектор n и вектор АВ коллинеарны.
Значит vector
О т в е т. -4х-у+2z=0 или 4х+у-2z=0
2) vector
Если плоскости перпендикулярны, их нормальные векторы тоже перпендикулярны.
Нормальные векторы перпендикулярны, значит скалярное произведение равно 0.
Скалярное произведение векторов, заданных своими координатами, равно сумме произведений одноименных координат.
1*2+(-4)*В+1*10=0
-4В=-12
В=3
О т в е т. При В=3.
Составьте уравнение плоскости, которая проходит через точку А и перпендикулярна прямой АВ. ГДЗ. Геометрия. 10 класс. Погорелов. § 4 п.38 Задача 65
Кто поможет с решением? Составьте уравнение плоскости, которая проходит через точку А и перпендикулярна прямой АВ, если:
1) А(-1; 1; 2), В(2; 0; 1);
2) А( 1; 0; -1), В(4; 6; -3);
3) А(3; -4; 5), В(2; 1; -3).
Лови уравнения.
1) п = АВ = (3; -1; -1)
Уравнение искомой плоскости: 3(х — (—1)) + (— 1 )(у — 1) + (-1)
(z — 2) = 0; 3х -у — z + 6 = 0
2) п = АВ = (3; 6; -2)
Уравнение искомой плоскости: 3(х — 1) +
+ 6(у — 0) + (-а )(z-(-l)) = 0; 3x + 6y-2z-5 =0.
3) п=AB = (-1; 5; -8)
Уравнение искомой плоскости: (-1)(x — 3) + 5(у — (- 4)) +
+ (- 8)(z — 5) = 0; — х + 5у — 8z + 63 = 0; х — 5у + 8z — 63 = 0
Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.
В этой статье мы поговорим о том, как составляется уравнение плоскости, проходящей через заданную точку трехмерного пространства перпендикулярно к заданной прямой. Сначала разберем принцип нахождения уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой, после чего подробно разберем решения характерных примеров и задач.
Навигация по странице.
Нахождение уравнения плоскости, проходящей через заданную точку пространства перпендикулярно к заданной прямой.
Поставим перед собой следующую задачу.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , задана точка 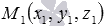
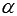
Сначала вспомним один важный факт.
На уроках геометрии в средней школе доказывается теорема: через заданную точку трехмерного пространства проходит единственная плоскость, перпендикулярная к данной прямой (доказательство этой теоремы Вы можете найти в учебнике геометрии за 10 — 11 классы, указанном в списке литературы в конце статьи).
Теперь покажем, как находится уравнение этой единственной плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.
Мы можем написать общее уравнение плоскости, если нам известны координаты точки, лежащей в этой плоскости, и координаты нормального вектора плоскости.
В условии задачи нам даны координаты x1 , y1 , z1 точки М1 , через которую проходит плоскость 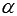
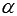
Любой направляющий вектор прямой a представляет собой нормальный вектор плоскости 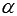
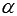
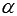
В свою очередь, координаты направляющего вектора прямой a могут определяться различными способами, зависящими от способа задания прямой a в условии задачи. Например, если прямую a в прямоугольной системе координат задают канонические уравнения прямой в пространстве вида 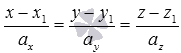
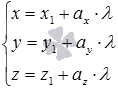
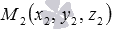
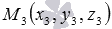
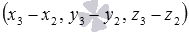
Итак, получаем алгоритм для нахождения уравнения плоскости 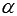
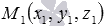
- находим координаты направляющего вектора прямой a (
);
- принимаем координаты направляющего вектора прямой a как соответствующие координаты нормального вектора
плоскости
(
, где
);
- записываем уравнение плоскости, проходящей через точку
и имеющей нормальный вектор
, в виде
— это и есть искомое уравнение плоскости, проходящей через заданную точку пространства перпендикулярно к заданной прямой.
Из найденного общего уравнения плоскости вида 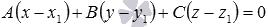
Примеры составления уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.
Рассмотрим решения нескольких примеров, в которых находится уравнение плоскости, проходящей через заданную точку пространства перпендикулярно к заданной прямой.
http://class.rambler.ru/temy-gdz/sostavte-uravnenie-ploskosti-kotoraya-prohodit-cherez-tochku-a-i-perpendikulyarna-pryamoy-av-gdz-geometriya-10-klass-pogorelov-4-p-38-zadacha-65-37667.htm
http://www.cleverstudents.ru/line_and_plane/plane_passes_through_point_perpendicular_to_line.html

 );
);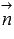 плоскости
плоскости 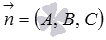 , где
, где 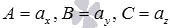 );
);