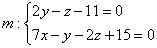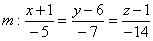5.6.3. Как найти ортогональную проекцию прямой на плоскость?
г) Во-первых, что это за проекция?
Проведём очередную физкульт-пятиминутку:
Пожалуйста, найдите дома швабру и поместите её между ног. Представьте, что она бесконечна. Подбородок плотно прижат к груди. Теперь строго перпендикулярно смотрим вниз на швабру. при этом получается такое умное лицо…. Все выполнили задание? Тень от швабры – это и есть её ортогональная проекция на пол.
На чертеже выше наша «швабра»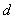 
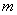
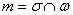
проведена малиновым цветом, а её проекция, прямая 
– коричневым цветом. Легко заметить, что проекция задаётся пересечением плоскостей: 
, и на самом деле ответ уже готов: 
Другое дело, что часто требуется представить уравнения прямой в канонической форме, это стандартная задача:
Точка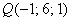 
, принадлежащая проекции, уже известна, осталось найти её направляющий вектор. Для быстроты используем формулу: 
Таким образом, канонические уравнения проекции: 
Как уже отмечалось, для решения этой задачи, не обязательно находить именно точку пересечения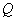 
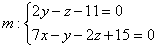
(лишняя работа). Нас устроит любая точка, принадлежащая проекции, и её легко подобрать из системы 
.
Есть и другой способ нахождения проекции, связанный с построением перпендикуляра к плоскости «сигма», но я тут прикинул, он вряд ли короче. Однако на всякий случай озвучу алгоритм, вдруг понадобится кому:
– находим точку пересечения прямой и плоскости: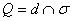 
(вот в этом способе уже обязательно находим);
– берём произвольную точку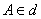 
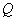
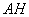
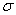
, не совпадающую с точкой 
) и опускаем из неё перпендикуляр 
на плоскость 
(см. следующие параграфы);
– находим основание перпендикуляра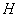 
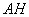
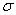
(как пересечение прямой 
и плоскости 
);
– составляем канонические уравнения проекции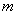 
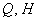
по двум точкам: 
.
Задача 31787 Найти проекцию прямой (x–2)/5 = (y–3)/1.
Условие
Найти проекцию прямой (x–2)/5 = (y–3)/1 = (z+1)/2 на плоскость x+4y–3z+7=0
Решение
Точка (2;3;-1) принадлежит данной прямой.
Составим уравнение прямой || нормальному вектору плоскости
vector
Найдем координаты точки K — точки пересечения этой прямой и плоскости Обозначим отношение подставим в уравнение плоскости Найдем координаты точки В — точки пересечения данной прямой и данной плоскости. Обозначим отношение подставим в уравнение плоскости Составляем уравнение прямой ВК, как уравнение прямой, проходящей через две точки Пусть в пространстве задана общая декартова система координат и две точки \(M_<1>\) и \(M_<2>\) с координатами \((x_<1>, y_<1>, z_<1>)\) и \((x_<2>, y_<2>, z_<2>)\). Чтобы написать уравнение прямой \(M_<1>M_<2>\), примем \(M_<1>\) за начальную точку, a \(\overrightarrow В планиметрии задача решается также. Отличие только в том, что координаты точек теперь \((x_<1>, y_<1>)\) и \((x_<2>, y_<2>)\), и мы получаем по формуле для прямой на плоскости Пусть \(M_<1>\), \(M_<2>\) и \(M_<3>\) — не лежащие на одной прямой точки с координатами \((x_<1>, y_<1>, z_<1>)\), \((x_<2>, y_<2>, z_<2>)\) и \((x_<3>, y_<3>, z_<3>)\) в общей декартовой системе координат. Выберем \(M_<1>\) в качестве начальной точки, a \(\overrightarrow Легко проверить, что все приведенные здесь условия являются не только необходимыми, но и достаточными. Из формулы \eqref Пусть даны плоскость \(P\) и определенный ее нормальный вектор \(\boldsymbol Если \(\boldsymbol Мы получим уравнение полупространства в координатной форме, если вспомним, что согласно утверждению 3 отсюда выражение \((\boldsymbol Плоскость \(P\) и вектор \(\boldsymbol Вот, однако, факт, не зависящий от выбора направления нормального вектора: если \(M_<1>(x_<1>, y_<1>, z_<1>)\) и \(M_<2>(x_<2>, y_<2>, z_<2>)\) две точки, не лежащие в плоскости, то результаты подстановки их координат в левую часть уравнения плоскости \(Ax_<1>+By_<1>+Cz_<1>+D\) и \(Ax_<2>+By_<2>+Cz_<2>+D\) имеют один знак тогда и только тогда, когда точки лежат в одном полупространстве. Для решения задач бывает полезно следующее замечание: если точка \(M_<0>(x_<0>, y_<0>, z_<0>)\) лежит на плоскости, то точка с координатами \(x_<0>+A\), \(y_<0>+B\), \(z_<0>+C\) лежит в “положительном” полупространстве. Иначе говоря, вектор с координатами \(A, B, C\) направлен в “положительное” полупространство. Это легко проверяется подстановкой. Вполне аналогично сказанному о полупространствах мы можем определить, что такое полуплоскость, и доказать, что неравенство \(Ax+By+Cz+D \geq 0\), связывающее декартовы координаты точки на плоскости, определяет полуплоскость. Вторая полуплоскость, ограниченная прямой \(Ax+By+C=0\), задается неравенством \(Ax+By+C \leq 0\). Точки \(M_<1>(x_<1>, y_<1>)\) и \(M_<2>(x_<2>, y_<2>)\) лежат по одну сторону от прямой тогда и только тогда, когда \((Ax_<1>+By_<1>+C)(Ax_<2>+By_<2>+C) > 0\). Пусть дана плоскость с уравнением \((\boldsymbol Если в декартовой прямоугольной системе координат точка \(M\) имеет координаты \((X, Y, Z)\), то равенство \eqref Рассмотрим прямую на плоскости, заданную уравнением \(Ax+By+C=0\) в декартовой прямоугольной системе координат. Пусть \(M_<0>(x_<0>, y_<0>)\) — начальная точка прямой, a \(M(X, Y)\) — некоторая точка плоскости. В качестве направляющего вектора возьмем вектор \(\boldsymbol(-B, A)\). Мы знаем (ранее доказывали), что площадь параллелограмма равна \(S=|(X-x_<0>)A-(Y-y_<0>)(-B)|\). Тогда по формуле \(S=|AX+BY+C|\) и Легко заметить также, что для нахождения расстояния от точки до прямой на плоскости можно воспользоваться формулой \eqref Чтобы найти угол между двумя прямыми, следует найти их направляющие векторы и вычислить косинус угла между ними, используя скалярное произведение. При этом следует иметь в виду, что, изменив направление одного из векторов, мы получим косинус смежного угла. Для нахождения угла между прямой и плоскостью определяют угол \(\theta\) между направляющим вектором прямой и нормальным вектором плоскости. Если векторы выбрать так, чтобы \(\cos \theta \geq 0\), и взять \(0 \leq \theta \leq \pi/2\), то искомый угол дополняет \(\theta\) до \(\pi/2\). Угол между плоскостями находят как угол между их нормальными векторами. Полезна бывает формула для угла между прямыми линиями на плоскости, заданными уравнениями \(y=k_<1>x+b_<1>\) и \(y=k_<2>x+b_<2>\) декартовой прямоугольной системе координат. Обозначим через \(\varphi\) угол между прямыми, отсчитываемый от первой прямой ко второй в том же направлении, в котором производится кратчайший поворот от первого базисного вектора ко второму. Тогда \(\operatorname Конечно, эта формула не имеет смысла, когда знаменатель дроби обращается в нуль. В этом случае прямые перпендикулярны. Действительно, векторы с компонентами \(1, k_<1>\) и \(1, k_<2>\) — направляющие векторы прямых, и их скалярное произведение равно \(1+k_<1>k_<2>\). Таким образом, верно следующее утверждение. Для перпендикулярности прямых с угловыми коэффициентами \(k_<1>\) и \(k_<2>\) в декартовой прямоугольной системе координат необходимо и достаточно выполнение равенства \(1+k_<1>k_<2>=0\). Если \((\boldsymbol Пучком прямых на плоскости называется множество прямых, проходящих через фиксированную точку — центр пучка. Пусть \(A_<1>x+B_<1>y+C_<1>=0\) и \(A_<2>x+B_<2>y+C_<2>=0\) — уравнения двух прямых, принадлежащих пучку. Тогда уравнение Основанием для этого служит следующее утверждение. При любых \(\alpha\) и \(\beta\) \((\alpha^<2>+\beta^ <2>\neq 0)\) уравнение \eqref Докажем сначала, что коэффициенты при переменных в уравнении \eqref Обозначим через \(x_<0>\), \(y_<0>\) координаты центра пучка. По условию Вторая часть предложения будет доказана, если окажется, что через любую точку, отличную от центра пучка \(M_<0>\), проходит прямая линия с уравнением вида \eqref Заметим, что каждая пара чисел \(\alpha\) и \(\beta\) \((\alpha^<2>+\beta^ <2>\neq 0)\) определяет в пучке единственную прямую, но каждой прямой соответствуют бесконечно много пропорциональных между собой пар чисел. Если нам известны координаты центра пучка, то уравнение пучка можно написать в виде Систему из уравнений прямых, определяющих пучок, можно рассматривать как уравнение центра пучка. Поэтому уравнение каждой прямой пучка есть следствие этой системы. Теперь наш результат можно сформулировать так. Если система линейных уравнений имеет решение., то некоторое линейное уравнение является ее следствием тогда и только тогда, когда оно есть сумма уравнений системы, умноженных на какие-то числа. Мы доказали это предложение для частного случая систем из двух уравнений с двумя неизвестными. В общем виде оно вытекает из результатов главы о системах линейных уравнений. Другими геометрическими интерпретациями этого предложения являются пучки и связки плоскостей. Пучком плоскостей называется множество плоскостей, проходящих через фиксированную прямую — ось пучка. Уравнение пучка плоскостей имеет вид Связкой плоскостей называется множество плоскостей, проходящих через фиксированную точку — центр связки. Уравнение связки плоскостей имеет вид Предположим, что на плоскости дана алгебраическая линия \(L\), имеющая в декартовой системе координат уравнение Может, конечно, случиться, что все коэффициенты этого уравнения равны нулю, и оно представляет собой тождество. Если исключить этот случай, то число корней уравнения и, следовательно, число точек пересечения не превосходит порядка линии. Таким образом, мы доказали следующее утверждение. Число точек пересечения алгебраической линии с прямой, которая на ней не лежит целиком, не превосходит порядка линии. Существуют линии, которые ни с одной прямой не имеют в принципе возможного числа точек пересечения, равного порядку линии. Примерами могут служить линии с уравнениями \(x^<2>+y^<2>=0\) или \((x^<2>+y^<2>)^<2>-1=0\). Архимедова спираль — линия с уравнением \(r=\alpha\varphi\) в полярной системе координат — пересекает каждую прямую, проходящую через полюс, в бесконечном числе точек. Следовательно, она не является алгебраической линией. http://reshimvse.com/zadacha.php?id=31787 http://univerlib.com/analytic_geometry/vector_algebra/basic_problems_about_lines_and_planes/
Решаем систему:
<(x-2)/1=(y-3)/4=(z-1)/(-3)
(x-2)/1=(y-3)/4=(z-1)/(-3) = λ ⇒
получим параметрические уравнения прямой
x= λ +2
y= 4λ +3
z=-3 λ +1
(x-2)/5=(y-3)/1=(z+1)/2=t ⇒
получим параметрические уравнения прямой
x=5t+2
y=t+3
z=2t+1
Основные задачи о прямых и плоскостях
Уравнение прямой, проходящей через две точки.
$$
\frac
$$
Если в этих равенствах какой-либо из знаменателей равен нулю, то следует приравнять нулю соответствующий числитель.
$$
\begin
x-x_<1>& y-y_<1>\\
x_<2>-x_<1>& y_<2>-y_<1>
\end
= 0.\nonumber
$$Уравнение плоскости, проходящей через три точки.
$$
\begin
x-x_<1>& y-y_<1>& z-z_<1>\\
x_<2>-x_<1>& y_<2>-y_<1>& z_<2>-z_<1>\\
x_<3>-x_<1>& y_<3>-y_<1>& z_<3>-z_<1>
\end
= 0.\label
$$Параллельность прямой и плоскости.
$$
\begin
A& B& C\\
A_<1>& B_<1>& C_<1>\\
A_<2>& B_<2>& C_<2>
\end
\neq 0.\label
$$
Действительно, это неравенство означает, что прямая, по которой пересекаются две плоскости, не параллельна третьей.Полупространство.
$$
Ax+By+Cz+D \geq 0.\nonumber
$$
Обратно, любое такое неравенство можно записать как \((\boldsymbolРасстояние от точки до плоскости.
$$
h=\frac<|(\boldsymbol
$$
$$
h=\frac<|AX+BY+CZ+D|><\sqrt
$$
Рис. 7.1. Расстояние от точки до плоскости.Расстояние от точки до прямой.
Рис. 7.2. Расстояние от точки до прямой.
$$
h=\frac<|AX+BY+C|><\sqrt
$$Расстояние между скрещивающимися прямыми.
Рис. 7.3. Расстояние между скрещивающимися прямымиВычисление углов.
$$
\operatorname
$$
Рис. 7.4. \(\varphi=\varphi_<2>-\varphi_<2>\)Некоторые задачи на построение.
Перпендикуляр из точки на плоскость. Проекция точки.
$$
\boldsymbol
$$
Таким образом, из радиус-вектоpa \(\boldsymbolПерпендикуляр из точки на прямую.
Уравнение проекции прямой на плоскость.
Общий перпендикуляр к двум скрещивающимся прямым.
Рис. 7.5. Перпендикуляр между скрещивающимися прямымиПучок прямых.
$$
\alpha(A_<1>x+B_<1>y+C_<1>)+\beta(A_<2>x+B_<2>y+C_<2>)=0\label
$$
при условии \(\alpha^<2>+\beta^ <2>\neq 0\) называется уравнением пучка прямых.
$$
(\alpha A_<1>+\beta A_<2>)x+(\alpha B_<1>+\beta B_<2>)y+(\alpha C_<1>+\beta C_<2>)=0.\nonumber
$$
Допустим, что \(\alpha A_<1>+\beta A_<2>=0\) и \(\alpha B_<1>+\beta B_<2>=0\). Так как прямые пересекаются, \(A_<1>B_<2>-A_<2>B_ <1>\neq 0\) и из утверждения о существовании решения системы уравнений вытекает, что значения \(\alpha=0\), \(\beta=0\) единственные, которые удовлетворяют этим двум равенствам. Но эти значения мы исключили. Таким образом, уравнение \eqref
$$
A_<1>x_<0>+B_<1>y_<0>+C_<1>=0,\ A_<2>x_<0>+B_<2>y_<0>+C_<2>=0,\nonumber
$$
а потому \(x_<0>\), \(y_<0>\) удовлетворяют уравнению \eqref
$$
u=A_<1>x_<1>+B_<1>y_<1>+C_<1>=0,\ v=A_<2>x_<1>+B_<2>y_<1>+C_<2>=0\nonumber
$$
Так как наши прямые имеют только одну общую точку, числа \(u\) и \(v\) одновременно не равны нулю, и мы вправе положить \(\alpha=-v\), \(\beta=-u\). При таких значениях \(\alpha\) и \(\beta\) координаты точки \(M_<1>\) удовлетворяют уравнению \eqref
$$
\alpha(x-x_<0>)+\beta(y-y_<0>)=0,\nonumber
$$
положив, что пучок определяется прямыми \(x-x_<0>=0\) и \(y-y_<0>=0\). Впрочем, и без того очевидно, что это — уравнение произвольной прямой, проходящей через \(M_<0>\).
$$
\alpha(A_<1>x+B_<1>y+C_<1>z+D_<1>)+\beta(A_<2>x+B_<2>y+C_<2>z+D_<2>)=0,\nonumber
$$
где \(\alpha^<2>+\beta^ <2>\neq 0\), а в скобках стоят левые части уравнений двух различных плоскостей пучка.
$$
\alpha(A_<1>x+B_<1>y+C_<1>z+D_<1>)+\beta(A_<2>x+B_<2>y+C_<2>z+D_<2>) +\\+ \gamma(A_<3>x+B_<3>y+C_<3>z+D_<3>)=0,\nonumber
$$
где \(\alpha^<2>+\beta^<2>+\gamma^ <2>\neq 0\), а в скобках стоят левые части уравнений плоскостей связки, имеющих центр своей единственной общей точкой.О геометрическом смысле порядка алгебраической линии.
$$
A_<1>x^x^
$$
Рассмотрим произвольную прямую с параметрическими уравнениями
$$
x=x_<0>+a_<1>t,\ y=y_<0>+a_<2>t.\label
$$
Найдем точки пересечения \(L\) и прямой линии. Они будут известны, если мы найдем соответствующие им значения параметра \(t\). Это будут те значения, при которых \(x\) и \(y\), выраженные по формулам \eqref
$$
A_<1>(x_<0>+a_<1>t)^(x_<0>+a_<1>t)^
$$
Раскрывая скобки в каждом члене, мы получим многочлены относительно \(t\) степеней \(k_<1>+l_<1>, …, k_+l_\). Их сумма будет многочленом, степень которого не выше, чем максимальная из степеней слагаемых. Но максимальное из чисел \(k_<1>+l_<1>,…,k_+l_\) — это порядок линии \(L\). Поэтому степень уравнения \eqref