Прямые на координатной плоскости
 Линейная функция Линейная функция |
 График линейной функции График линейной функции |
 Прямые, параллельные оси ординат Прямые, параллельные оси ординат |
 Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые |
Линейная функция
Линейной функцией называют функцию, заданную формулой
| y = kx + b, | (1) |
где k и b – произвольные (вещественные) числа.
При любых значениях k и b графиком линейной функции является прямая линия .
Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .
График линейной функции
При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.
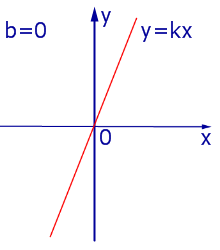 |
| Рис.1 |
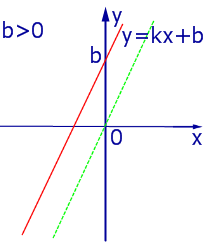 |
| Рис.2 |
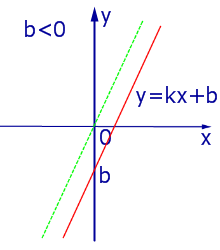 |
| Рис.3 |
При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.
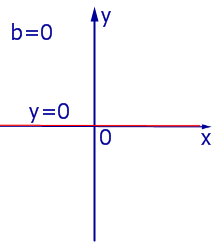 |
| Рис.4 |
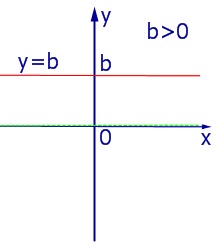 |
| Рис.5 |
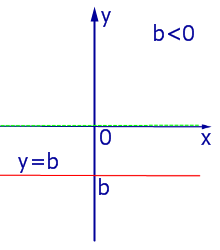 |
| Рис.6 |
При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.
| k y = kx + b1 и y = kx + b2 , имеющие одинаковые угловые коэффициенты и разные свободные члены имеющие разные угловые коэффициенты y = kx + b1 и перпендикулярны при любых значениях свободных членов. Угловой коэффициент прямой линии
равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).
Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b . При Прямые, параллельные оси ординатПрямые, параллельные оси Oy , задаются формулой
где c – произвольное число, и изображены на рис. 13, 14, 15.
Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .; Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
где p, q, r – произвольные числа. В случае, когда что и требовалось. В случае, когда откуда вытекает, что уравнение (4) задает прямую линию вида (3). В случае, когда q = 0, p = 0, уравнение (4) имеет вид
и при r = 0 его решением являются точки всей плоскости: В случае, когда Замечание 2 . При любом значении r1 , не совпадающем с r прямая линия, заданная уравнением
параллельна прямой, заданной уравнением (4) . Замечание 3 . При любом значении r2 прямая линия, заданная уравнением
перпендикулярна прямой, заданной уравнением (4) . Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и
В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде
где r1 – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство Итак, уравнение прямой, параллельной к прямой В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде
где r2 – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство Составьте уравнения, графиками которых являются прямые AB, CD и EF, изображённые на рисунке 5?Математика | 5 — 9 классы Составьте уравнения, графиками которых являются прямые AB, CD и EF, изображённые на рисунке 5. Решение Вашего задания во вложении.
Графиком уравнения является прямая MN а графиком второго уравнения прямая KP составьте систему уравнений найдите решение уравнений и докажите что оно еденственное?Графиком уравнения является прямая MN а графиком второго уравнения прямая KP составьте систему уравнений найдите решение уравнений и докажите что оно еденственное. Решите, пожалуйста?Я буду Вам ояень благодарна * . * Запишите формулой линейные функции, графики которых прямые a, b, и c, изображённые на рисунке 4. Составьте формулу прямой пропорциональности графиком которой является прямая АВ проходящая через точку — 6 9) помогите))?Составьте формулу прямой пропорциональности графиком которой является прямая АВ проходящая через точку — 6 9) помогите)). Составьте уравнения, графиками которых являются прямые AB, CD и EF, изображённые на рисунке?Составьте уравнения, графиками которых являются прямые AB, CD и EF, изображённые на рисунке. На рисунке изображён график функции?На рисунке изображён график функции. На рисунке изображены прямые а d и c запишите формулы функции, графиками которых являются данные прямые?На рисунке изображены прямые а d и c запишите формулы функции, графиками которых являются данные прямые. Прямые AB и CD, EF и KL, изображённые на рисунке 6?Прямые AB и CD, EF и KL, изображённые на рисунке 6. 24 взаимно перпендикулярные прямые. Найдите градусные меры углов COF и FOB. Пересекаются ли изображённые на рисунке : отрезок EF и луч ST?Пересекаются ли изображённые на рисунке : отрезок EF и луч ST? Запишите уравнения прямых AB, CD и EF, изображенных на рисунке 9?Запишите уравнения прямых AB, CD и EF, изображенных на рисунке 9. 6. Помогите пожалуйста! Прямые AB и CD, EF и KL, изображённые на рисунке 7?Прямые AB и CD, EF и KL, изображённые на рисунке 7. 25, взаимно перпендикулярны. Найдите градусные меры углов COF и FOB. Если вам необходимо получить ответ на вопрос Составьте уравнения, графиками которых являются прямые AB, CD и EF, изображённые на рисунке 5?, относящийся к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу. В категории Математика вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы. S = v * t — формула пути — — — — — — — — — — — — — — — — — — — — 1) 35 : 5 = 7 (км / ч) — скорость парохода по течению реки ; 2) 35 : 7 = 5 (км / ч) — скорость парохода против течения реки ; 3) (7 + 5) : 2 = 6 (км / ч) — собственная скорость парохода.. 1. ) Сколько желтых роз вырастили ребята? 48 — 6 = 42(р. ) Ответ : 42 розы. 48 : 6 = 8(роз. ) — желтых. 3 + 4 + 2 + 6 = 15 частей всего 30 : 15 = 2 стакана одна часть 2 * 4 = 8 стаканов грибов. 250 / 10 = 25 платьев 25 + 2 = 27 пальто шили в день 27 * 10 = 270пальто за 10 дней. 12 / 2 = 6 (шт. ) — было значков 12 + 6 = 18(шт. ) — было открыток Ответ : 18 открыток было у Ани. Хм 1) 12 : 2 = 6 (з) — было значков 2) 12 + 6 = 18 (открыток) ответ : 18. Нет нельзя потому что лир не меняется. Очевидно, что в такую картинку превращается число, у которого первая цифра нечетная, а вторая делится на 4 нечетных цифр : 5 (1, 3, 5, 7, 9) цифр, делящихся на 4 : 3 (0, 4, 8) всего чисел : 5 * 3 = 15 Ответ : 15 чисел. 983102 \ 10000 = 98, 3102 50932102 \ 1000000 = 50, 932102 611007 \ 10000 = 6, 11007 64953344 \ 1000000 = 64, 953344. 4.13. Уравнения прямых на координатной плоскостиДавайте рассмотрим такие функций, графики которых имеют вид прямых. Простоты ради, мы будем иметь дело с безразмерными величинами, а значит, в качестве осей у нас будут выступать простые числовые прямые, и все наши чертежи мы будем делать на обычной координатной плоскости. Прямая, проходящая через начало координат Построение графика по заданной функции Пусть переменная \(y\) пропорциональна переменной \(x\) с коэффициентом пропорциональности \(k\) : Давайте договоримся, что \(x\) здесь — это независимая переменная, а \(y\) — зависимая. Коэффициент \(k\) играет роль константы (параметра). В таких случаях говорят, что \(y\) является (однородной) линейной функцией от \(x\) . Графиком этой функции, как мы хорошо знаем, является прямая, проходящая через начало координат \((0, 0)\) . Для построения этой прямой нам достаточно определить еще какую-либо одну ее точку \((x_1, y_1)\) . Для этого положим, например, \(x_1 = 1\) . Тогда \(y_1 = k \cdot 1 = k\) . Проводим через эту точку и начало координат прямую линию. Это и есть график функции \(y\) от \(x\) . Так, по крайней мере, обстоит дело в теории, а на практике точку \((x_1, y_1)\) лучше брать настолько далеко от начала координат, насколько позволяет чертеж. В этом стучае прямую удается провести наиболее точно. Ниже приведен пример такого построения для функции \(y=\frac<1> <2>x\) . Восстановление функции по графику Решим теперь обратную задачу. Пусть на координатной плоскости с осями \(x\) и \(y\) нам дана прямая, проходящая через начало координат. Спрашивается: графиком какой функции она является? При этом подразумевается, что функция должна быть задана в виде формулы, связывающей переменные \(x\) и \(y\) . Такая формула носит название уравнения графика функции. В данном случае речь идет об уравнении прямой, проходящей через точку \((0,0)\) . Заранее ясно, что это уравнение имеет вид От нас фактически только требуется найти значение константы \(k\) . Для этого отметим на прямой произвольную точку, отличную от \((0,0)\) , и определим ее координаты \((x_1, y_1).\) Эти координаты, очевидно, связаны соотношением При этом следует особо подчеркнуть, что константа \(k\) не зависит от выбора точки \((x_1, y_1).\) Какую бы точку на прямой мы не выбрали в качестве \((x_1, y_1),\) мы придем к одному и тому же значению \(k\) . Таким образом, Пример нахождения уравнения прямой приведен на следующем рисунке. Отметим два особых случая. Во-первых, прямая может совпасть с осью \(x\) . Тогда значение \(y\) остается постоянным и равным нулю на всем ее протяжении. Тем не менее наше общее решение остается в силе. При этом оказывается, что \(k = 0\) и переменную \(y\) можно всё еще формально считать функцией от \(x\) : Во-вторых, прямая может совпасть с осью \(y\) . В этом случае в каждой ее точке \(x = 0\) . Формула для константы \(k\) оказывается неприменимой, потому что число \(x_0\) , стоящее в знаменателе, обращается в нуль. Приходится признать, что мы не можем подобрать такую функцию \(y\) от \(x\) , которая имела бы подобный график. Разве что, мы можем теперь принять \(y\) за независимую переменную и формально рассматривать \(x\) как функцию от \(y<:>\) Несложно убедиться, что всякая точка, лежащая на оси \(y\) , удовлетворяет этому равенству. Заметим, что если бы мы захотели написать уравнение прямой, проходящей через начало координат, в самом общем виде, то мы могли бы это сделать так: Это соотношение между \(x\) и \(y\) остается справедливым в обоих рассмотренных частных случаях, однако выбор параметров не является однозначным, так как в качестве пары чисел \((x_1, y_1)\) можно взять координаты любой точки, принадлежащей прямой. Произвольная прямая Восстановление функции по графику Начнем с обратной задачи. Пусть теперь на координатной плоскости дана произвольная прямая, не проходящая через начало координат. Вопрос нас будет интересовать всё тот же: графиком какой функции она является или, короче говоря, каково уравнение этой прямой? Отметим на прямой две любые несовпадающие точки и обозначим их координаты через \((x_0, y_0)\) и \((x_1,y_1)\) . Поместим в точку \((x_0, y_0)\) начало новой системы координат с осями \(x’\) и \(y’\) , сонаправленными с соответствующими осями \(x\) и \(y\) старой системы. Тогда координаты другой отмеченной точки в новой системе окажутся равны \(\begin Вообще, как мы знаем, новые («штрихованные») координаты любой точки связаны со старыми («нештрихованными») координатами соотношением Наша прямая проходит через начало координат новой системы, поэтому мы можем сразу же выписать ее уравнение в «штрихованных» переменных: Переходя к «нештрихованным» переменным, получаем Что и решает поставленную задачу. При желании, можно еще выразить функцию \(y\) от \(x\) в явном виде: \(y = k\,x — k\,x_0 + y_0\) \(y = k\,x + b,\) где \(b = — k\,x_0 + y_0.\) Значения констант \(k\) и \(b\) не зависят от выбора точек \((x_0, y_0)\) и \((x_1,y_1)\) . Какие бы точки на заданной прямой мы не взяли, мы всегда придем к одним и тем же значениям \(k\) и \(b\) . Заметим, что из-за дополнительного слагаемого \(b\) переменные \(x\) и \(y\) не пропорциональны друг другу. Поэтому константа \(k\) называется теперь не коэффициентом пропорциональности, как это было раньше, а угловым коэффициентом. Название это происходит от того, что значение \(k\) тесно связано с углом наклона прямой по отношению к оси \(x\) . Чем круче идет прямая, тем больше ее угловой коэффициент. Константу \(b\) иногда называют свободным членом. Как легко видеть, переменная \(y\) равна \(b\) при \(x = 0\) . Иными словами, \(b\) — это точка на оси \(y\) , в которой эта ось пересекается с нашей прямой. Если \(b = 0\) , то прямая проходит через начало координат, и мы возвращаемся к частному случаю, рассмотренному ранее. Из наших рассуждений следует, что любая прямая на координатной плоскости может быть описана уравнением вида при подходящем выборе констант \(k\) и \(b\) . Единственным исключением является особый случай, когда в выражении для углового коэффициента \(k = \frac \(x = 0 \cdot (y — y_0) + x_0.\) В совершенно общем виде уравнение прямой можно написать следующим образом: \((x_1-x_0) (y-y_0) = (y_1-y_0) (x-x_0).\) При этом, однако, выбор двух пар параметров \((x_0, y_0)\) и \((x_1, y_1)\) (которые, по смыслу, являются координатами двух произвольных точек, лежащих на прямой) неоднозначен. Построение графика по заданной функции Теперь давайте выясним, как построить график неоднородной линейной функции \(y\) от \(x\) , которая определяется как где \(k\) и \(b\) — любые действительные числа. Как мы только что выяснили, к такому виду сводится уравнение произвольной прямой (при условии, что она не параллельна оси \(y\) ). Строго говоря, это не исключает, что при некоторых значения параметров \(k\) и \(b\) график этой функции может отличаться от прямой линии. Давайте убедимся, что этого никогда не происходит. Перепишем данное нам уравнение следующим образом: Если перейти в новую, штрихованную, систему координат с началом в точке \((0, b)\) и с осями \(x’\) и \(y’\) , сонаправленными с соответствующими осями старой системы, то в новых координатах уравнение примет вид: Мы получим тогда не что иное, как уравнение пропорциональной зависимости, которое гарантировано задает прямую линию. Значит, и график неоднородной линейной функции представляет собой прямую линию при любых значениях параметров \(k\) и \(b\) . Но для того, чтобы построить прямую, достаточно знать две ее произвольные точки \((x_0, y_0)\) и \((x_1, y_1)\) . В качестве \(x_0\) и \(x_1\) можно взять, например, соответственно ноль и единицу. Тогда \(y_0 = b\) (при \(x_0 = 0\) ), Проводим прямую через точки \((x_0, y_0)\) и \((x_1, y_1)\) — и задача решена. На практике, впрочем, лучше брать такие точки, которые расположены друг от друга по возможности дальше, насколько позволяет чертеж. Пример графика неоднородной линейной функции со значением параметров \(k = \frac<1><3>\) и \(b = 1\) представлен на следующем рисунке. Конспект \(1\) . Линейная функция \(y = k\,x + b\) называется однородной при \(b = 0\) и неоднородной при \(b \ne 0.\) Ее график на координатной плоскости представляет собой прямую линию, которая строится по двум произвольным точкам. \(2\) . Уравнение прямой, проходящей через начало координат: \(y = \frac \(3\) . Уравнение произвольной прямой: \(y-y_0 = \frac источники: http://matematika.my-dict.ru/q/569114_sostavte-uravnenia-grafikami-kotoryh-avlautsa-pramye/ http://www.nekin.info/math/m0413.htm |

 , параллельны .
, параллельны . , пересекаются при любых значениях свободных членов.
, пересекаются при любых значениях свободных членов.



 прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле
прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле



 уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .
уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .

 получаем:
получаем:

 уравнение (5) решений вообще не имеет.
уравнение (5) решений вообще не имеет.

















