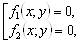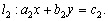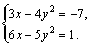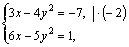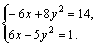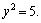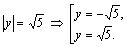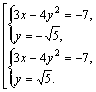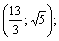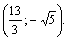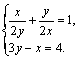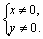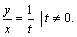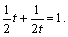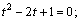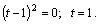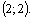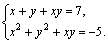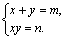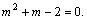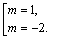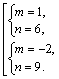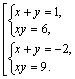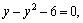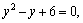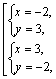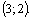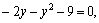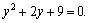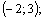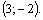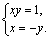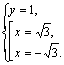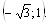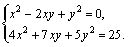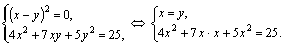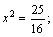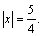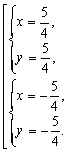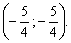Методы решения систем уравнений с двумя переменными
п.1. Метод подстановки
Вариант 1
Шаг 1. Из одного уравнения выразить y через x: y(x).
Шаг 2. Подставить полученное выражение во второе уравнение и найти x.
Шаг 3. Подставить найденный x в y(x) и найти y.
Шаг 4. Записать полученные пары решений. Работа завершена.
Вариант 2
Шаг 1. Из одного уравнения выразить x через y: x(y).
Шаг 2. Подставить полученное выражение во второе уравнение и найти y.
Шаг 3. Подставить найденный y в x(y) и найти x.
Шаг 4. Записать полученные пары решений. Работа завершена.
п.2. Метод сложения
п.3. Метод замены переменных
Иногда удобно ввести новые переменные и решить систему для них.
А затем, вернуться к исходным переменным и найти их значения.
п.4. Графический метод
Графический метод подробно рассмотрен в §15 данного справочника.
п.5. Примеры
Пример 1. Решите систему уравнений:
а) \( \left\< \begin
Решаем методом подстановки: \( \left\< \begin
Для нижнего уравнения: \( \mathrm
Подставляем в верхнее уравнение: \( \mathrm
б) \( \left\< \begin
Замена переменных: \( \left\< \begin
Выразим (x 2 + y 2 ) через a и b:
x 2 + y 2 = (x 2 + y 2 + 2xy) – 2xy = (x + y) 2 – 2xy = a 2 – 2b
Подставляем: \( \left\< \begin
Решаем нижнее уравнение: 2b 2 – 9b + 10 = 0 $$ \mathrm< D=9^2-4\cdot 2\cdot 10=1,\ \ b=\frac<9\pm 1><4>> = \left[\begin
21. Системы и совокупности уравнений
Пусть даны два уравнения с двумя неизвестными 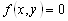
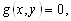
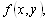
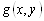
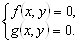
Решить систему (3.15) – значит найти все пары чисел 
Аналогично определяется понятие системы с тремя и более неизвестными.
Системы, все уравнения которых однородные, называются Однородными системами уравнений.
Система называется Совместной, если она имеет хотя бы одно решение и Несовместной, если таких решений не существует.
Две системы уравнений Эквивалентны (Равносильны), если они имеют одни и те же решения или обе не имеют решений.
Над уравнениями системы можно выполнять следующие действия, преобразующие данную систему в эквивалентную ей:
1) менять порядок следования уравнений;
2) умножать на число 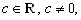
3) умножать на число 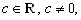
Несколько уравнений образуют Совокупность уравнений
Если ставится задача найти все те решения, которые удовлетворяют хотя бы одному уравнению совокупности и входят в область определения остальных уравнений.
Система двух линейных уравнений с двумя неизвестными имеет вид:

Где
Геометрически каждому уравнению системы (3.16) соответствует прямая линия на плоскости:
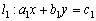
1) если 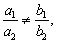
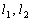
2) если 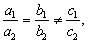
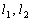
3) если 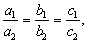
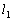
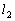
Основными методами решения систем уравнений (3.15) являются:
1) метод подстановки;
2) метод исключения неизвестной;
3) метод сложения;
4) метод умножения (деления) уравнений;
5) метод замены переменных;
6) графический метод.
Пример 1. Решить систему
Решение. Решим методом сложения. Для этого первое уравнение системы умножим на 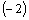
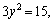
Заданная система сводится к решению совокупности систем:
Ее решением являются пары чисел:
Пример 2. Решить систему
Решение. ОДЗ:
Заменим в первом уравнении системы 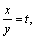
Получим дробно-рациональное уравнение:
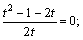
Возвращаемся к переменным Х, У:
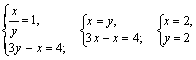
Получили ответ
Пример 3. Решить систему
Решение. Данная система относится к Симметрическим системам (неизвестные 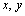
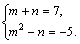
Далее используем метод сложения:
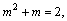
Получаем корни этого квадратного уравнения:
С учетом системы (3.17) имеем:
Возвращаясь к переменным Х, У, получаем:
Решим записанные системы отдельно:
1) 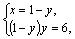
Возвращаясь к системе (3.18), получаем:
Т. е. имеем два решения 
2) 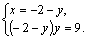
Поскольку для последнего квадратного уравнения 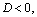
Получили ответ
Пример 4. Решить систему графически:
1) 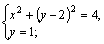
2)
Решение. 1) Исходя из геометрического смысла, 
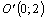
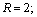
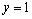
Построим эти линии (рис. 3.2).
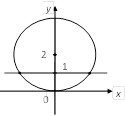 |
Графики имеют две точки пересечения, т. е. система имеет два решения, которые найдем из системы (3.20):
Получили ответ
2) Уравнение 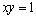
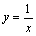
Уравнение 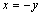
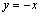
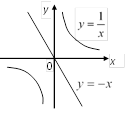
Графики не имеют точек пересечения и, следовательно, система решений не имеет.
Пример 5. Решить систему
Решение. Система содержит однородное уравнение.
Так как 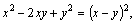
Из второго уравнения найдем Х:
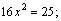
Получаем совокупность двух систем:
Приходим к ответу 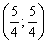
Совокупности уравнений, неравенств, систем: определение, как решить
Тема совокупностей уравнений и др. систем, как правило, в рамках школьного курса представлена скупо. В 10-11 классе она изучается совсем недолго. Мы считаем, что это неверный подход, поскольку совокупности — прекрасный способ оформления привычных решений при работе с неравенствами и уравнениями, поэтому в рамках статьи мы раскроем этот вопрос.
В данной статье мы сформулируем общее понятие совокупностей неравенств, уравнений и их систем, а также их комбинации. Кроме определений здесь, как обычно, есть решения задач, наглядно поясняющие тот или иной фрагмент текста.
Понятие совокупности
Для того, чтобы хорошо понимать, что такое совокупность уравнений, нужно вспомнить еще одно понятие из школьного курса алгебры — система уравнений (аналогично неравенствам). Тогда определения совокупности покажутся вам знакомыми и легко усвоятся.
Проанализировав несколько учебников, выберем наиболее удачное определение:
Совокупность уравнений представляет собой несколько уравнений, записанных друг под другом и объединенных квадратной скобкой. Значение этой записи таково: совокупность объединяет такие значения переменных, при которых хотя бы одно из входящих в нее уравнений превращается в верное равенство.
Сравним между собой понятие совокупности и понятие системы:
- Запись совокупности, как мы уже говорили выше, осуществляется с помощью квадратной скобки, а системы записываются с фигурной.
- Совокупность включает в себя множество решений, которые относятся хотя бы одному из уравнений, входящих в ее состав. Система объединяет решения, которые подходят для каждого уравнения.
Пример 1
Вот примеры совокупности уравнений:
x + 1 = 0 , x 2 — 1 = — 8 x + y 2 + z 4 = 0 , x · y · z = 0 , z = 5
Иногда при записи совокупности можно обойтись и без квадратной скобки: так часто делают в школе. В таком случае уравнения можно просто указать через запятую. Для примера выше это может быть запись вида x + y 2 + z 4 = 0 , x · y · z = 0 , z = 5 .
Понятие совокупности неравенств формулируется схожим образом.
Совокупность неравенств представляет собой несколько неравенств, записанных друг под другом и объединенных квадратной скобкой. Она включает в себя решения, которые подходят хотя бы для одного из неравенств, входящих в состав совокупности.
Приведем пример такой записи:
x + 3 > 0 , 2 · x + 3 ≤ 0 , 5
Схожее определение для этого понятия упоминается в учебнике Мордковича.
Если необходимо, то можно указать, сколько уравнений (неравенств) входят в состав совокупности, а также сколько в ней участвует переменных. Вид уравнения (неравенства) также может быть внесен в запись при необходимости. Сформулируем название совокупности из примера: это совокупность 2-х неравенств с одной переменной, а ее составные части — это целые рациональные первой степени.
Сочетать в рамках одной совокупности можно не только записи одного вида. Так, имеет право на существование совокупность, состоящая из двух неравенств и одного уравнения, сочетание одного неравенства с системой уравнений, двух систем неравенств и др. Главная задача — сохранить неизменным основной смысл совокупности: в нее входят такие решения, которые подходят хотя бы для одной составляющей совокупности.
В качестве примера смешанных совокупностей приведем две:
x > 3 x 8 x — 5 x ≤ — 2 x 2 = 9 x 2 > 5 ( x — 6 ) · ( x — 8 ) = 0 x ≤ 3 x 2 + 2 · x — 8 > 0
Что такое решение совокупности
Решение — главная составляющая совокупности. Сформулируем, что же такое решения совокупности с разным количеством переменных.
Решение совокупности с одной переменной представляет собой значение этой переменной, которое является решением хотя бы одной составляющей совокупности (уравнения, неравенства).
Если мы возьмем совокупность уравнений, значит, его решение — это значение x , при котором хотя бы одно из уравнений, входящих в состав совокупности, обращается в верное равенство.
Возьмем неравенство x > 1 , x 2 ≥ 4 · x + 2 . Для него решением, например, будет тройка, т.к. она больше единицы, и, следовательно, она — верное решение для первого неравенства. А если мы возьмем ноль, то увидим, что ни к одному из неравенств он не подходит; значит, 0 в качестве решения совокупности мы рассматривать не можем , ведь запись вида 0 > 1 и x 2 ≥ 4 · x + 2 неверна.
Решение совокупности, в которую входит две, три и более переменных, — это две, три и более переменных, которые подходят в качестве решения хотя бы одному компоненту совокупности.
Возьмем еще один пример, посложнее. У нас есть совокупность:
x 2 + y 2 = 4 , x + y > 0 , x ≥ 3
Значения 3 и 0 будут верными решениями совокупности: они подходят в качестве верных значений в уравнения 2 и 3 ( 3 + 0 > 0 и 3 ≥ 3 — верно). А вот значения 2 и 1 не есть решение совокупности: ни к 1 , ни ко 2 , ни к 3 они не подойдут.
В некоторых учебниках можно встретить также понятия общего и частного решения совокупности; под частным при этом понимается одно решение, а под общим — их некое множество. Но более употребительно понятие просто решения совокупности, а о том, общее оно или частное, можно понять из контекста.
Также нужно отметить следующее: объединение решений всех компонентов совокупности также есть решение совокупности. Напомним, что решение системы представляет собой пересечение решений ее компонентов.
В продолжение темы мы советуем вам материал «Равносильные совокупности».
http://matica.org.ua/metodichki-i-knigi-po-matematike/algebraicheskie-uravneniia-i-neravenstva-funktcii-logarifmy/21-sistemy-i-sovokupnosti-uravnenii
http://zaochnik.com/spravochnik/matematika/systems/sovokupnosti-uravnenij-neravenstv-sistem-i-tp/