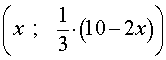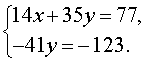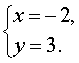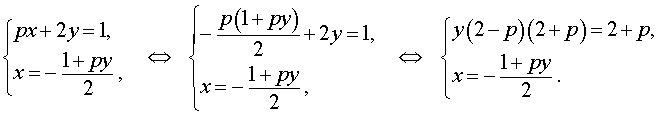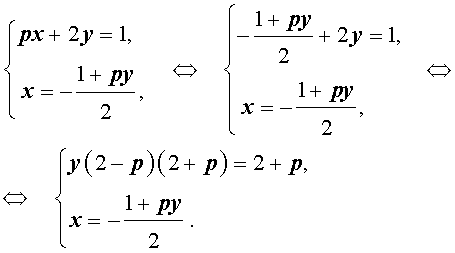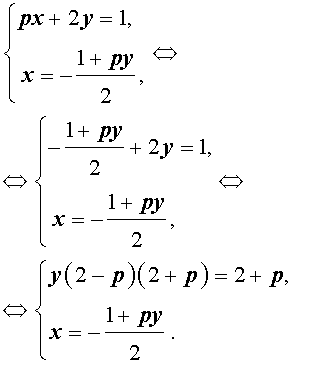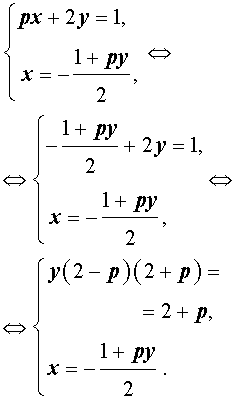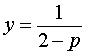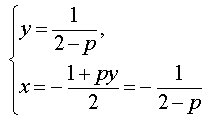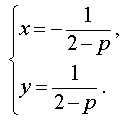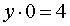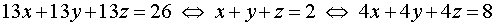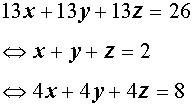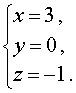Системы линейных уравнений
 Линейные уравнения (уравнения первой степени) с двумя неизвестными Линейные уравнения (уравнения первой степени) с двумя неизвестными |
 Системы из двух линейных уравнений с двумя неизвестными Системы из двух линейных уравнений с двумя неизвестными |
 Системы из трех линейных уравнений с тремя неизвестными Системы из трех линейных уравнений с тремя неизвестными |
Линейные уравнения (уравнения первой степени) с двумя неизвестными
Определение 1 . Линейным уравнением (уравнением первой степени) с двумя неизвестными x и y называют уравнение, имеющее вид
| ax +by = c , | (1) |
где a , b , c – заданные числа.
Определение 2 . Решением уравнения (1) называют пару чисел (x ; y) , для которых формула (1) является верным равенством.
Пример 1 . Найти решение уравнения
| 2x +3y = 10 | (2) |
Решение . Выразим из равенства (2) переменную y через переменную x :
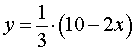 | (3) |
Из формулы (3) следует, что решениями уравнения (2) служат все пары чисел вида
где x – любое число.
Замечание . Как видно из решения примера 1, уравнение (2) имеет бесконечно много решений. Однако важно отметить, что не любая пара чисел (x ; y) является решением этого уравнения. Для того, чтобы получить какое-нибудь решение уравнения (2), число x можно взять любым, а число y после этого вычислить по формуле (3).
Системы из двух линейных уравнений с двумя неизвестными
Определение 3 . Системой из двух линейных уравнений с двумя неизвестными x и y называют систему уравнений, имеющую вид
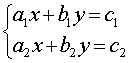 | (4) |
Определение 4 . В системе уравнений (4) числа a1 , b1 , a2 , b2 называют коэффициентами при неизвестных , а числа c1 , c2 – свободными членами .
Определение 5 . Решением системы уравнений (4) называют пару чисел (x ; y) , являющуюся решением как одного, так и другого уравнения системы (4).
Определение 6 . Две системы уравнений называют равносильными (эквивалентными) , если все решения первой системы уравнений являются решениями второй системы, и все решения второй системы являются решениями первой системы.
Равносильность систем уравнений обозначают, используя символ «
Системы линейных уравнений решают с помощью метода последовательного исключения неизвестных , который мы проиллюстрируем на примерах.
Пример 2 . Решить систему уравнений
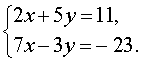 | (5) |
Решение . Для того, чтобы решить систему (5) исключим из второго уравнения системы неизвестное х .
С этой целью сначала преобразуем систему (5) к виду, в котором коэффициенты при неизвестном x в первом и втором уравнениях системы станут одинаковыми.
Если первое уравнение системы (5) умножить на коэффициент, стоящий при x во втором уравнении (число 7 ), а второе уравнение умножить на коэффициент, стоящий при x в первом уравнении (число 2 ), то система (5) примет вид
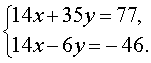 | (6) |
Теперь совершим над системой (6) следующие преобразования:
- первое уравнение системы оставим без изменений;
- из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.
В результате система (6) преобразуется в равносильную ей систему
Из второго уравнения находим y = 3 , и, подставив это значение в первое уравнение, получаем
Пример 3 . Найти все значения параметра p , при которых система уравнений
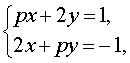 | (7) |
а) имеет единственное решение;
б) имеет бесконечно много решений;
в) не имеет решений.
Решение . Выражая x через y из второго уравнения системы (7) и подставляя полученное выражение вместо x в первое уравнение системы (7), получим
Следовательно, система (7) равносильна системе
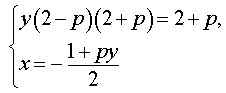 | (8) |
Исследуем решения системы (8) в зависимости от значений параметра p . Для этого сначала рассмотрим первое уравнение системы (8):
| y (2 – p) (2 + p) = 2 + p | (9) |
Если 
Следовательно, система (8) равносильна системе
Таким образом, в случае, когда 
Если p = – 2 , то уравнение (9) принимает вид
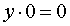
и его решением является любое число 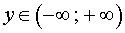
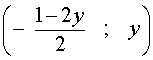
где y – любое число.
Если p = 2 , то уравнение (9) принимает вид
и решений не имеет, откуда вытекает, что и система (7) решений не имеет.
Системы из трех линейных уравнений с тремя неизвестными
Определение 7 . Системой из трех линейных уравнений с тремя неизвестными x , y и z называют систему уравнений, имеющую вид
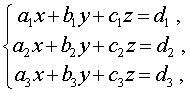 | (10) |
Определение 9 . Решением системы уравнений (10) называют тройку чисел (x ; y ; z) , при подстановке которых в каждое из трех уравнений системы (10) получается верное равенство.
Пример 4 . Решить систему уравнений
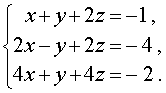 | (11) |
Решение . Будем решать систему (11) при помощи метода последовательного исключения неизвестных .
Для этого сначала исключим из второго и третьего уравнений системы неизвестное y , совершив над системой (11) следующие преобразования:
- первое уравнение системы оставим без изменений;
- ко второму уравнению прибавим первое уравнение и заменим второе уравнение системы на полученную сумму;
- из третьего уравнения вычтем первое уравнение и заменим третье уравнение системы на полученную разность.
В результате система (11) преобразуется в равносильную ей систему
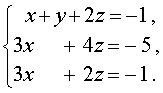 | (12) |
Теперь исключим из третьего уравнения системы неизвестное x , совершив над системой (12) следующие преобразования:
- первое и второе уравнения системы оставим без изменений;
- из третьего уравнения вычтем второе уравнение и заменим третье уравнение системы на полученную разность.
В результате система (12) преобразуется в равносильную ей систему
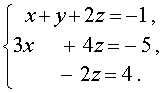 | (13) |
Из системы (13) последовательно находим
Пример 5 . Решить систему уравнений
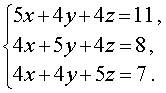 | (14) |
Решение . Заметим, что из данной системы можно получить удобное следствие, сложив все три уравнения системы:
Если числа (x ; y ; z) являются решением системы (14), то они должны удовлетворять и уравнению (15). Однако в таком случае числа (x ; y ; z) должны также быть решением системы, которая получается, если из каждого уравнения системы (14) вычесть уравнение (15):
Поскольку мы использовали следствие из системы (14), не задумываясь о том, являются ли сделанные преобразования системы (14) равносильными, то полученный результат нужно проверить. Подставив тройку чисел (3 ; 0 ; –1) в исходную систему (14), убеждаемся, что числа (3 ; 0 ; –1) действительно являются ее решением.
Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы с нелинейными уравнениями» и нашим учебным пособием «Системы уравнений».
Системы уравнений: определение, виды, примеры решения
Статья знакомит с таким понятием, как определение системы уравнений и ее решением. Будут рассмотрены часто встречающиеся случаи решений систем. Приведенные примеры помогут подробно пояснить решение.
Определение системы уравнений
Чтобы перейти к определению системы уравнений, необходимо обратить внимание на два момента: вид записи и ее смысл. Чтобы понять это, нужно подробно остановиться на каждом из видов, тогда сможем прийти к определению систем уравнений.
Например, возьмем два уравнения 2 · x + y = − 3 и x = 5 , после чего объединим фигурной скобкой такого плана:
2 · x + y = — 3 , x = 5 .
Уравнения, объединенные фигурной скобкой, считаются записями систем уравнений. Они задают множества решений уравнений данной системы. Каждое решение должно являться решением всех заданных уравнений.
Другими словами это означает, что любые решения первого уравнения будут решениями всех уравнений, объединенных системой.
Системы уравнений – это некоторое количество уравнений, объединенных фигурной скобкой, имеющих множество решений уравнений, которые одновременно являются решениями для всей системы.
Основные виды систем уравнений
Видов уравнений достаточно много, как систем уравнений. Для того, чтобы было удобно решать и изучать их, подразделяют на группы по определенным характеристикам. Это поможет в рассмотрении систем уравнений отдельных видов.
Для начала уравнения классифицируются по количеству уравнений. Если уравнение одно, то оно является обычным уравнением, если их более, тогда имеем дело с системой, состоящей из двух или более уравнений.
Другая классификация затрагивает число переменных. Когда количество переменных 1 , говорят, что имеем дело с системой уравнений с одной неизвестной, когда 2 – с двумя переменными. Рассмотрим пример
x + y = 5 , 2 · x — 3 · y = 1
Очевидно, что система уравнений включает в себя две переменные х и у .
При записи таких уравнений считается число всех переменных, имеющихся в записи. Их наличие в каждом уравнении необязательно. Хотя бы одно уравнение должно иметь одну переменную. Рассмотрим пример системы уравнений
2 x = 11 , x — 3 · z 2 = 0 , 2 7 · x + y — z = — 3
Данная система имеет 3 переменные х , у , z . Первое уравнение имеет явный х и неявные у и z . Неявные переменные – это переменные, имеющие 0 в коэффициенте. Второе уравнение имеет х и z , а у неявная переменная. Иначе это можно записать таким образом
2 x + 0 · y + 0 · z = 11
А другое уравнение x + 0 · y − 3 · z = 0 .
Третья классификация уравнений – это вид. В школе проходят простые уравнения и системы уравнений, начиная с систем двух линейных уравнений с двумя переменными. Имеется в виду, что система включает в себя 2 линейных уравнения. Для примера рассмотрим
2 · x — y = 1 , x + 2 · y = — 1 и — 3 · x + y = 0 . 5 , x + 2 2 3 · y = 0
Это основные простейшие линейные уравнения. Далее можно столкнуться с системами, содержащими 3 и более неизвестных.
В 9 классе решают уравнения с двумя переменными и нелинейные. В целых уравнениях повышается степень для увеличения сложности. Такие системы называют системами нелинейных уравнений с определенным количеством уравнений и неизвестных. Рассмотрим примеры таких систем
x 2 — 4 · x · y = 1 , x — y = 2 и x = y 3 x · y = — 5
Обе системы с двумя переменными и обе являются нелинейными.
При решении можно встретить дробно-рациональные уравнения. Например
x + y = 3 , 1 x + 1 y = 2 5
Могут называть просто системой уравнений без уточнения, каких именно. Редко уточняют сам вид системы.
Старшие классы переходят к изучению иррациональных, тригонометрических и показательных уравнений. Например,
x + y — x · y = 5 , 2 · x · y = 3 , x + y = 5 · π 2 , sin x + cos 2 y = — 1 , y — log 3 x = 1 , x y = 3 12 .
Высшие учебные заведения изучают и исследуют решения систем линейных алгебраических уравнений (СЛАУ). Левая часть таких уравнений содержит многочлены с первой степенью, а правая – некоторые числа. Отличие от школьных в том, что количество переменных и количество уравнений может быть произвольным, чаще всего несовпадающим.
Решение систем уравнений
Решение системы уравнений с двумя переменными – это пара переменных, которая при подстановке обращает каждое уравнение в верное числовое неравенство, то есть является решением для каждого уравнения данной системы.
К примеру, пара значений х = 5 и у = 2 являются решением системы уравнений x + y = 7 , x — y = 3 . Потому как при подстановке уравнения обращаются в верные числовые неравенства 5 + 2 = 7 и 5 − 2 = 3 . Если подставить пару х = 3 и у = 0 , тогда система не будет решена, так как подстановка не даст верное уравнение, а именно, мы получим 3 + 0 = 7 .
Сформулируем определение для систем, содержащих одну и более переменных.
Решение системы уравнений с одной переменной – это значение переменной, которая является корнем уравнений системы, значит, все уравнения будут обращены в верные числовые равенства.
Рассмотрим на примере системы уравнений с одной переменной t
t 2 = 4 , 5 · ( t + 2 ) = 0
Число — 2 – решение уравнения, так как ( − 2 ) · 2 = 4 , и 5 · ( − 2 + 2 ) = 0 являются верными числовыми равенствами. При t = 1 система не решена, так как при подстановке получим два неверных равенства 12 = 4 и 5 · ( 1 + 2 ) = 0 .
Решение системы с тремя и более переменными называют тройку, четверку и далее значений соответственно, которые обращают все уравнения системы в верные равенства.
Если имеем значения переменных х = 1 , у = 2 , z = 0 , то подставив их в систему уравнений 2 · x = 2 , 5 · y = 10 , x + y + z = 3 , получим 2 · 1 = 2 , 5 · 2 = 10 и 1 + 2 + 0 = 3 . Значит, эти числовые неравенства верные. А значения ( 1 , 0 , 5 ) не будут решением, так как, подставив значения, второе из них будет неверное, как и третье: 5 · 0 = 10 , 1 + 0 + 5 = 3 .
Системы уравнений могут не иметь решений вовсе или иметь бесконечное множество. В этом можно убедиться при углубленном изучении данной тематики. Можно прийти к выводу, что системы уравнений – это пересечение множеств решений всех ее уравнений. Раскроем несколько определений:
Несовместной называют систему уравнений, когда она не имеет решений, в противном случае ее называют совместной.
Неопределенной называют систему, когда она имеет бесконечное множество решений, а определенной при конечном числе решений либо при их отсутствии.
Такие термины редко применяются в школе, так как рассчитаны для программ высших учебных заведений. Знакомство с равносильными системами углубит имеющиеся знания по решению систем уравнений.
Методы решения систем уравнений с двумя переменными
п.1. Метод подстановки
Вариант 1
Шаг 1. Из одного уравнения выразить y через x: y(x).
Шаг 2. Подставить полученное выражение во второе уравнение и найти x.
Шаг 3. Подставить найденный x в y(x) и найти y.
Шаг 4. Записать полученные пары решений. Работа завершена.
Вариант 2
Шаг 1. Из одного уравнения выразить x через y: x(y).
Шаг 2. Подставить полученное выражение во второе уравнение и найти y.
Шаг 3. Подставить найденный y в x(y) и найти x.
Шаг 4. Записать полученные пары решений. Работа завершена.
п.2. Метод сложения
п.3. Метод замены переменных
Иногда удобно ввести новые переменные и решить систему для них.
А затем, вернуться к исходным переменным и найти их значения.
п.4. Графический метод
Графический метод подробно рассмотрен в §15 данного справочника.
п.5. Примеры
Пример 1. Решите систему уравнений:
а) \( \left\< \begin
Решаем методом подстановки: \( \left\< \begin
Для нижнего уравнения: \( \mathrm
Подставляем в верхнее уравнение: \( \mathrm
б) \( \left\< \begin
Замена переменных: \( \left\< \begin
Выразим (x 2 + y 2 ) через a и b:
x 2 + y 2 = (x 2 + y 2 + 2xy) – 2xy = (x + y) 2 – 2xy = a 2 – 2b
Подставляем: \( \left\< \begin
Решаем нижнее уравнение: 2b 2 – 9b + 10 = 0 $$ \mathrm< D=9^2-4\cdot 2\cdot 10=1,\ \ b=\frac<9\pm 1><4>> = \left[\begin
http://zaochnik.com/spravochnik/matematika/systems/sistemy-uravnenij-nachalnye-svedenija/
http://reshator.com/sprav/algebra/9-klass/metody-resheniya-sistem-uravnenij-s-dvumya-peremennymi/