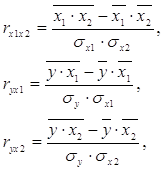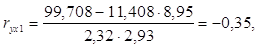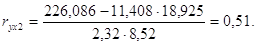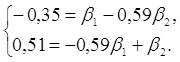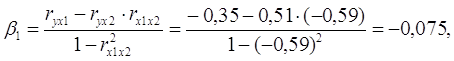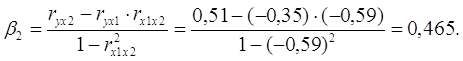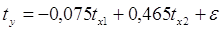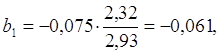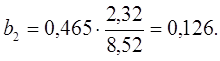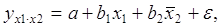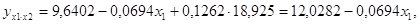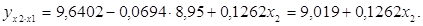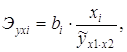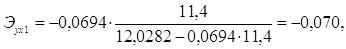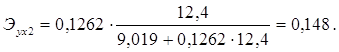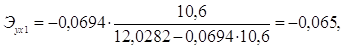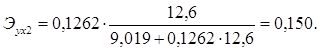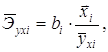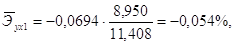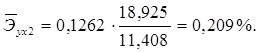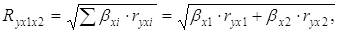Стандартизованное уравнение регрессии экономический смысл коэффициентов

Стандартизованное уравнение регрессии экономический смысл коэффициентов

Существует и другая возможность оценки роли группировочных признаков, их значимости для классификации на основе стандартизованных коэффициентов регрессии или коэффициентов раздельной детерминации (см. гл. 8). [c.147]

Теснота парной линейной корреляционной связи, как и любой другой показатель, может быть измерена корреляционным отношением ц. Кроме того, при линейной форме уравнения применяется другой показатель тесноты связи — коэффициент корреляции г . Этот показатель представляет собой стандартизованный коэффициент регрессии, т. е. коэффициент, выраженный не в абсолютных единицах измерения признаков, а в долях среднего квадратического отклонения результативного признака [c.241]

Коэффициенты условно-чистой регрессии bf являются Именованными числами, выраженными в разных единицах измерения, и поэтому несравнимы друг с другом. Для преобразования их в сравнимые относительные показатели применяется то же преобразование, что и для получения коэффициента парной корреляции. Полученную величину называют стандартизованным коэффициентом регрессии или -коэффициентом. [c.270]

На практике часто бывает необходимо сравнение влияния на зависимую переменную различных объясняющих переменных, когда последние выражаются разными единицами измерения. В этом случае используют стандартизованные коэффициенты регрессии b j и коэффициенты эластичности Ej Q = 1,2. р) [c.90]

Стандартизованный коэффициент регрессии b j показывает, на сколько величин sy изменится в среднем зависимая переменная Y при увеличении только j-й объясняющей переменной на sx, a [c.90]

Решение. Для сравнения влияния каждой из объясняющих переменных по формуле (4.10) вычислим стандартизованные коэффициенты регрессии [c.90]

Необходимо а) найти множественный коэффициент детерминации и пояснить его смысл 6) найти уравнение множественной регрессии Y по Х и Xi, оценить значимость этого уравнения и его коэффициентов на уровне а=0,05 в) сравнить раздельное влияние на зависимую переменную каждой из объясняющих переменных, используя стандартизованные коэффициенты регрессии и коэффициенты эластичности г) найти 95%-ные доверительные интервалы для коэффициентов регрессии, а также для среднего и индивидуальных значений себестоимости 1 т литья в цехах, в которых выработка литья на одного работающего составляет 40 т, а брак литья — 5%. [c.107]

К уравнению множественной регрессии в стандартизованном масштабе применим МНК. Стандартизованные коэффициенты регрессии (Р-коэффициенты) определяются из следующей системы уравнений [c.50]

Определите частные коэффициенты эластичности и стандартизованные коэффициенты регрессии. [c.89]

Определите стандартизованные коэффициенты регрессии. [c.91]

В парной зависимости стандартизованный коэффициент регрессии есть не что иное, как линейный коэффициент корреляции fa Подобно тому, как в парной зависимости коэффициенты регрессии и корреляции связаны между собой, так и во множественной регрессии коэффициенты чистой регрессии й, связаны со стандартизованными коэффициентами регрессии / ,-, а именно [c.107]

Рассмотренный смысл стандартизованных коэффициентов регрессии позволяет их использовать при отсеве факторов — из модели исключаются факторы с наименьшим значением jQy. [c.108]

Как было показано выше, ранжирование факторов, участвующих в множественной линейной регрессии, может быть проведено через стандартизованные коэффициенты регрессии (/ -коэффициенты). Эта же цель может быть достигнута с помощью частных коэффициентов корреляции — для линейных связей. При нелинейной взаимосвязи исследуемых признаков эту функцию выполняют частные индексы детерминации. Кроме того, частные показатели корреляции широко используются при решении проблемы отбора факторов целесообразность включения того или иного фактора в модель доказывается величиной показателя частной корреляции. [c.121]

Рассчитанные по рекуррентной формуле частные коэффициенты корреляции изменяются в пределах от —1 до +1, а по формулам через множественные коэффициенты детерминации — от 0 до 1. Сравнение их друг с другом позволяет ранжировать факторы по тесноте их связи с результатом. Частные коэффициенты корреляции, подтверждая ранжировку факторов по их воздействию на результат, на основе стандартизованных коэффициентов регрессии /3-коэффициентов) в отличие от последних дают конкретную меру тесноты связи каждого фактора с результатом в чистом виде. Если из стандартизованного уравнения регрессии Л = Дч q + V 2 + з г з следует, что , > 2 > /3XJ, т. е. по силе влияния на результат порядок факторов таков Х , х2, х3, то этот же порядок факторов определяется и по соотношению частных коэффициентов корреляции, ГуХ] хт > г 2, Х ХЗ > г хт. [c.127]

Иными словами, в двухфакторном анализе частные коэффициенты корреляции — это стандартизованные коэффициенты регрессии, умноженные на корень квадратный цз соотношения долей остаточных дисперсий фиксируемого фактора на фактор и на результат. [c.128]

В процессе разработки нормативов численности собираются исходные данные о списочной численности управленческого персонала и значениях факторов по отобранным базовым предприятиям. Далее отбираются существенные факторы для каждой функции на основе корреляционного анализа, исходя из значения коэффициентов корреляции. Выбираются факторы с наибольшим значением парного коэффициента корреляции с функцией и стандартизованного коэффициента регрессии. [c.276]

Стандартизованные коэффициенты регрессии (р) рассчитываются для каждой функции по совокупности всех аргументов согласно формуле [c.75]

Тем не менее, в статистике даются полезные рекомендации, позволяющие получить хотя бы оценочные представления по этому поводу. В качестве примера познакомимся с одним из таких методов — сравнение стандартизованных коэффициентов регрессии. [c.71]

В общем случае все коэффициенты регрессии Ъ, Ь2,. . bk могут быть выражены в разных единицах измерения. Тем самым непосредственное их сравнение становится фактически некорректным, поскольку, скажем, формально меньший по величине коэффициент на деле может оказаться важнее большего. Короче говоря, в данной ситуации мы сталкиваемся с классической проблемой попытки сравнения кита и слона . Стандартизованные коэффициенты регрессии позволяют решить эту проблему за счет представления коэффициентов регрессии в некоторых кодированных единицах измерения. [c.71]

Стандартизованный коэффициент регрессии вычисляется путем умножения коэффициента регрессии bi на стандартное отклонение Sn (для наших -переменных обозначим его как Sxk) и деления полученного произведения на Sy. Это означает, что каждый стандартизованный коэффициент регрессии измеряется как величина b Sxk / .Применительно к нашему примеру получим следующие результаты (табл.10). [c.71]

Стандартизованные коэффициенты регрессии [c.72]

Таким образом, приведенное сравнение абсолютных величин стандартизованных коэффициентов регрессии позволяет получить пусть и довольно грубое, но достаточно наглядное представление о важности рассматриваемых факторов. Еще раз напомним, что эти результаты не являются идеальными, поскольку не в полной мере отражают реальное влияние исследуемых переменных (мы оставляем без внимания факт возможного взаимодействия этих факторов, что может исказить первоначальную картину). [c.72]

Коэффициенты этого уравнения (blf 62, Ь3) определяются решением стандартизованного уравнения регрессии [c.153]

Оператор 5. Вычисление -коэффициентов — коэффициентов регрессии в стандартизованном масштабе. [c.78]

Коэффициенты регрессии в (4.14) несопоставимы между собой, а / -коэффициенты уже сопоставимы. Поэтому для аналитика именно стандартизованное представление уравнения регрессии имеет особую значимость, поскольку позволяет дать сравнительную характеристику значимости факторов чем больше значение / -коэффициента, тем более существен фактор с позиции влияния его на результативный показатель. Бета-коэффициенты могут использоваться для установления нормативов, разработки весовых коэффициентов при конструировании различных сложных аналитических показателей (например, уровень научно-технического прогресса). [c.125]

На основании коэффициентов регрессии в стандартизованном масштабе (9.6), показывающих силу влияния каждого фактора, [c.198]

Но уравнения регрессии в стандартизованном и натуральном масштабах еще не позволяют решить две важные задачи. Очевидно, что для множественной регрессии, как и для парной, при любых коэффициентах регрессии разброс эмпирических точек вокруг поверхности регрессии может быть любым. Это приводит к тому, что во-первых, необходимо определить степень соответствия выбранного вида теоретической регрессии эмпирическому распределению или же (при фиксированном виде регрессии) определить уровень тесноты связи анализируемого показателя и группы изучаемых факторов. Поскольку же все факторы воздействуют на исследуемый показатель одновременно и мы не можем экспериментально отделить влияние одного фактора от влияния другого, возникает проблема, во-вторых, найти степень тесноты связи между изучаемым показателем и каждым фактором, предполагая, что все остальные заданы на постоянном уровне. [c.131]

Нетрудно видеть, что путем замены на 2 и дальнейших простых преобразований можно прийти к системе нормальных уравнений в стандартизованном масштабе. Подобное преобразование мы будем применять в дальнейшем, поскольку нормирование, с одной стороны, позволяет нам избежать слишком больших чисел и, с другой стороны, сама вычислительная схема при определении коэффициентов регрессии становится стандартной. [c.136]

Вид графа непосредственных связей говорит о том, что при построении уравнения регрессии только по двум факторам — количеству тралений и времени чистого траления— остаточная дисперсия ст .з4 не отличалась бы от остаточной дисперсии а .23456. полученной из уравнения регрессии, построенного по всем факторам. Чтобы оценить различие, мы обратимся в данном случае к выборочной оценке. 1.23456 = 0,907, а 1.34 = 0,877. Но если скорректировать коэффициенты по формуле (38), то 1.23456=0,867, a / i.34= = 0,864. Различие вряд ли можно считать существенным. Более того, г14 = 0,870. Это наводит на мысль, что количество тралений почти не оказывает непосредственного влияния на размер улова. Действительно, в стандартизованном масштабе 1.34 = 0,891 4 — 0,032 3- Нетрудно убедиться, что коэффициент регрессии при t3 недостоверен даже при очень низком доверительном интервале. [c.187]

Оценки коэффициентов регрессии для стандартизованных переменных получаются из решения системы уравнений [c.252]

Рп — стандартизованные коэффициенты множественной регрессии находятся из условия [c.125]

Рх/. — соответствующий коэффициент уравнения множественной регрессии в стандартизованном масштабе. [c.122]

Разработку многофакторной модели начинаем с определения коэффициентов уравнения множественной регрессии между результатами и факторными признаками в стандартизованном масштабе. [c.178]

Коэффициенты множественной регрессии в стандартизованном масштабе находим из системы линейных уравнений [c.179]

Применение в практических целях уравнения множественной регрессии в стандартизованном масштабе затруднительно, поэтому уравнение множественной регрессии следует перевести в натуральный масштаб. Перевод коэффициентов множественной регрессии из стандартизованного масштаба в натуральный производится по формуле [c.180]

Построить уравнение множественной регрессии в стандартизованной и естественной форме рассчитать частные коэффициенты эластичности, сравнить их с Pj и р2 > пояснить различия между ними. [c.56]

Согласованность частной корреляции и стандартизованных коэффициентов регрессии наиболее отчетливо видна из сопоставления их формул при двухфакгорном анализе. Для уравнения [c.127]

Связь коэффициентов множественной регрессии Ьг со стандартизованными коэффициентами р описьшается соотношением [c.50]

Коэффициенты Sj являются специальным типом частных коэффициентов регрессии. Коэффициенту является стандартизованным коэффициентом р-регрессии. Будем называть ру коэффициентом влияния (согласно С. Райту), понимая при этом, что Ру есть числовая величина, которая измеряет долю стандартного отклонения /-й эндогенной переменной (следствия) с соответствующим знаком, обусловленную влияниему-й экзогенной переменной (причины) в том смысле, что если произвести измерение этого влияния при измененииу-й переменной в тех же условиях, что и в данных наблюдениях и при неизменных прочих условиях (включая постоянное воздействие фактора xui), то полученный результат будет равен рф [c.215]

Конспект лекций по курсу «Эконометрика» для студентов III курса дневного отделения всех специальностей (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ФИНАНСОВО – ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

Кафедра статистики и эконометрики

по курсу «ЭКОНОМЕТРИКА»

для студентов III курса дневного отделения

Печатается по решению кафедры прогнозирования и статистики : протокол от 01.01.2001 г.

МОДЕЛЬ МНОЖЕСТВЕННОЙ РЕГРЕССИИ

На любой экономический показатель чаще всего оказывает влияние не один, а несколько факторов. Например, спрос на некоторое благо определяется не только ценой данного блага, но и ценами на замещающие и дополняющие блага, доходом потребителей и многими другими факторами. В этом случае вместо парной регрессии рассматривается множественная регрессия

(1)

Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и в ряде других вопросов экономики. В настоящее время множественная регрессия – один из наиболее распространенных методов в эконометрике. Основной целью множественной регрессии является построение модели с большим числом факторов, а также определение влияния каждого фактора в отдельности и совокупного их воздействия на моделируемый показатель.

Множественный регрессионный анализ является развитием парного регрессионного анализа в случаях, когда зависимая переменная связана более чем с одной независимой переменной. Большая часть анализа является непосредственным расширением парной регрессионной модели, но здесь также появляются и некоторые новые проблемы, из которых следует выделить две. Первая проблема касается исследования влияния конкретной независимой переменной на зависимую переменную, а также разграничения её воздействия и воздействий других независимых переменных. Второй важной проблемой является спецификация модели, которая состоит в том, что необходимо ответить на вопрос, какие факторы следует включить в регрессию (1), а какие – исключить из неё. В дальнейшем изложение общих вопросов множественного регрессионного анализа будем вести, разграничивая эти проблемы. Поэтому вначале будем полагать, что спецификация модели правильна.

Самой употребляемой и наиболее простой из моделей множественной регрессии является линейная модель множественной регрессии:

(2)

По математическому смыслу коэффициенты в уравнении (2) равны частным производным результативного признака y по соответствующим факторам:

,,…,.

Параметр α называется свободным членом и определяет значение y в случае, когда все объясняющие переменные равны нулю. Однако, как и в случае парной регрессии, факторы по своему экономическому содержанию часто не могут принимать нулевых значений, и значение свободного члена не имеет экономического смысла. При этом, в отличие от парной регрессии, значение каждого регрессионного коэффициента равно среднему изменению y при увеличении x j на одну единицу лишь при условии, что все остальные факторы остались неизменными. Величина ε представляет собой случайную ошибку регрессионной зависимости.

Попутно отметим, что наиболее просто можно определять оценки параметров , изменяя только один фактор xj , оставляя при этом значения других факторов неизменными. Тогда задача оценки параметров сводилась бы к последовательности задач парного регрессионного анализа по каждому фактору. Однако такой подход, широко используемый в естественнонаучных исследованиях, (физических, химических, биологических), в экономике является неприемлемым. Экономист, в отличие от экспериментатора – естественника, лишен возможности регулировать отдельные факторы, поскольку не удаётся обеспечить равенство всех прочих условий для оценки влияния одного исследуемого фактора.

Получение оценок параметров уравнения регрессии (2) – одна из важнейших задач множественного регрессионного анализа. Самым распространенным методом решения этой задачи является метод наименьших квадратов (МНК). Его суть состоит в минимизации суммы квадратов отклонений наблюдаемых значений зависимой переменной y от её значений , получаемых по уравнению регрессии. Поскольку параметры являются случайными величинами, определить их истинные значения по выборке невозможно. Поэтому вместо теоретического уравнения регрессии (2) оценивается так называемое эмпирическое уравнение регрессии, которое можно представить в виде:

(3)

Здесь — оценки теоретических значений , или эмпирические коэффициенты регрессии, е – оценка отклонения ε . Тогда расчетное выражение имеет вид:

(4)

Пусть имеется n наблюдений объясняющих переменных и соответствующих им значений результативного признака:

(5)

Для однозначного определения значений параметров уравнения (4) объем выборки n должен быть не меньше количества параметров, т. е. . В противном случае значения параметров не могут быть определены однозначно. Если n=p +1, оценки параметров рассчитываются единственным образом без МНК простой подстановкой значений (5) в выражение (4). Получается система ( p +1) уравнений с таким же количеством неизвестных, которая решается любым способом, применяемым к системам линейных алгебраических уравнений (СЛАУ). Однако с точки зрения статистического подхода такое решение задачи является ненадежным, поскольку измеренные значения переменных (5) содержат различные виды погрешностей. Поэтому для получения надежных оценок параметров уравнения (4) объём выборки должен значительно превышать количество определяемых по нему параметров. Практически, как было сказано ранее, объём выборки должен превышать количество параметров при xj в уравнении (4) в 6-7 раз.

Для проведения анализа в рамках линейной модели множественной регрессии необходимо выполнение ряда предпосылок МНК. В основном это те же предпосылки, что и для парной регрессии, однако здесь нужно добавить предположения, специфичные для множественной регрессии:

50.Спецификация модели имеет вид (2).

60.Отсутствие мультиколлинеарности: между объясняющими переменными отсутствует строгая линейная зависимость, что играет важную роль в отборе факторов при решении проблемы спецификации модели.

70.Ошибки имеют нормальное распределение . Выполнимость этого условия нужна для проверки статистических гипотез и построения интервальных оценок.

При выполнимости всех этих предпосылок имеет место многомерный аналог теоремы Гаусса – Маркова: оценки , полученные по МНК, являются наиболее эффективными (в смысле наименьшей дисперсии) в классе линейных несмещенных оценок.

Оценка параметров линейного уравнения множественной регрессии

Рассмотрим три метода расчета параметров множественной линейной регрессии.

1. Матричный метод. Представим данные наблюдений и параметры модели в матричной форме.

— n – мерный вектор – столбец наблюдений зависимой переменной;

— ( p +1) – мерный вектор – столбец параметров уравнения регрессии (3);

— n – мерный вектор – столбец отклонений выборочных значений yi от значений , получаемых по уравнению (4).

Для удобства записи столбцы записаны как строки и поэтому снабжены штрихом для обозначения операции транспонирования.

Наконец, значения независимых переменных запишем в виде прямоугольной матрицы размерности :

Каждому столбцу этой матрицы отвечает набор из n значений одного из факторов, а первый столбец состоит из единиц, которые соответствуют значениям переменной при свободном члене.

В этих обозначениях эмпирическое уравнение регрессии выглядит так:

(6)

Отсюда вектор остатков регрессии можно выразить таким образом:

(7)

Таким образом, функционал , который, собственно, и минимизируется по МНК, можно записать как произведение вектора – строки е’ на вектор – столбец е :

(8)

В соответствии с МНК дифференцирование Q по вектору В приводит к выражению:

(9)

которое для нахождения экстремума следует приравнять к нулю. В результате преобразований получаем выражение для вектора параметров регрессии:

10)

Здесь — матрица, обратная к .

Пример. Бюджетное обследование пяти случайно выбранных семей дало следующие результаты (в тыс. руб.):

Построение уравнения регрессии в стандартизованном масштабе

4.2 Построение уравнения регрессии в стандартизованном масштабе

Параметры множественной регрессии можно определить другим способом, когда на основе матрицы парных коэффициентов корреляции строится уравнение регрессии в стандартизованном масштабе:

,

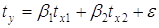
Применяя МНК к уравнению множественной регрессии в стандартизованном масштабе, после соответствующих преобразований получим систему нормальных уравнений вида:

где rух1, rух2 – парные коэффициенты корреляции.

Парные коэффициенты корреляции найдем по формулам:

Система уравнений имеет вид:

Решив систему методом определителей, получили формулы:

Уравнение в стандартизированном масштабе имеет вид:

Таким образом, с ростом уровня бедности на 1 сигму при неизменном среднедушевом доходе населения, общий коэффициент рождаемости уменьшится на 0,075 сигмы; а с увеличением среднедушевого дохода населения на 1 сигму при неизменном уровне бедности, общий коэффициент рождаемости возрастет на 0,465 сигмы.

Во множественной регрессии коэффициенты «чистой» регрессии bi связаны со стандартизованными коэффициентами регрессии βi следующим образом:

.

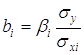
5. Частные уравнения регрессии

5.1 Построение частных уравнений регрессии

Частные уравнения регрессии связывают результативный признак с соответствующими факторами х при закреплении других учитываемых во множественной регрессии факторов на среднем уровне. Частные уравнения имеют вид:

.

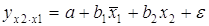
В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, т.к. другие факторы закреплены на неизменном уровне.

В данной задаче частные уравнения имеют вид:

5.2 Определение частных коэффициентов эластичности

На основе частных уравнений регрессии можно определить частные коэффициенты эластичности для каждого региона по формуле:

Рассчитаем частные коэффициенты эластичности для Калининградской и Ленинградской областей.

Для Калининградской области х1=11,4, х2=12,4, тогда:

Для Ленинградской области х1 =10,6, х2=12,6:

Таким образом, в Калининградской области при увеличении уровня бедности на 1%, общий коэффициент рождаемости сократится на 0,07%, а при увеличении среднедушевых доходов на 1%, общий коэффициент рождаемости возрастет на 0,148%. В Ленинградской области при увеличении уровня бедности на 1%, общий коэффициент рождаемости сократится на 0,065%, а при увеличении среднедушевых доходов на 1%, общий коэффициент рождаемости возрастет на 0,15%.

5.3 Определение средних коэффициентов эластичности

Средние по совокупности показатели эластичности находим по формуле:

Для данной задачи они окажутся равными:

Таким образом, с ростом уровня бедности на 1%, общий коэффициент рождаемости в среднем по совокупности сократится на 0,054% при неизменном среднедушевом доходе. При увеличении среднедушевого дохода на 1%, общий коэффициент рождаемости в среднем по изучаемой совокупности возрастет на 0,209% при неизменном уровне бедности.

6. Множественная корреляция

6.1 Коэффициент множественной корреляции

Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – коэффициента детерминации. Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, т.е. оценивает тесноту связи совместного влияния факторов на результат.

Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции. При линейной зависимости признаков формула индекса корреляции может быть представлена следующим выражением:

Ryx1x2 =.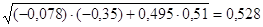

Таким образом, связь общего коэффициента рождаемости с уровнем бедности и среднедушевым доходом слабая.