Парная регрессия и корреляция. Функциональная и статистическая зависимость. Сущность регрессионного анализа.
Парная регрессия представляет собой регрессию между двумя переменными – y и x , т. е. модель вида: y f x = (y), где y – зависимая переменная (результативный признак); x – независимая, или объясняющая, переменная (признак-фактор). Знак «^» означает, что между переменными x и y нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина y складывается из двух слагаемых: ɵ x y y = + ε , где y – фактическое значение результативного признака; ɵ x y – теоретическое значение результативного признака, найденное исходя из уравнения регрессии; ε – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии. Случайная величина ε называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных. От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака ɵ x y , подходят к фактическим данным y . К ошибкам спецификации относятся неправильный выбор той или иной математической функции для ɵ x y и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной.
Если зависимость между признаками указывает на линейную корреляцию, рассчитывают коэффициент корреляции r, который позволяет оценить тесноту связи переменных величин, а также выяснить, какая доля изменений признака обусловлена влиянием основного признака, какая – влиянием других факторов. Коэффициент варьирует в пределах от –1 до +1. Если r=0, то связь между признаками отсутствует. Равенство r=0 говорит лишь об отсутствии линейной корреляционной зависимости, но не вообще об отсутствии корреляционной, а тем более статистической зависимости. Если r = ±1, то это означает наличие полной (функциональной) связи. При этом все наблюдаемые значения располагаются на линии регрессии, которая представляет собой прямую.
Практическая значимость коэффициента корреляции определяется его величиной, возведенной в квадрат, получившая название коэффициента детерминации.
Выборочный коэффициент корреляции определяется равенством
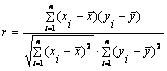
где хi, уi – варианты (наблюдавшиеся значения) признаков Х и Y; n – объем выборки; 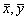
Функциональная зависимость – это связь, при которой каждому значению независимой переменной х соответствует точно определенное значение зависимой переменной y
Статистическая зависимость – это связь, при которой каждому значению независимой переменной х соответствует множество значений зависимой переменной y, причем неизвестно заранее, какое именно значение примет y
Регрессионный анализ заключается в определении аналитической формы связи, в которой изменение результативного признака обусловлено влиянием одного или нескольких факторных признаков, а множество всех прочих факторов, также оказывающих влияние на результативный признак, принимается за постоянные и средние значения
Оценка функциональной зависимости условного среднего значения результативного признака от факторных признаков.
Основной предпосылкой регрессионного анализа является то, что только результативный признак подчиняется нормальному закону распределения, а факторные признаки – произвольному закону распределения.
Уравнение регрессии, или модель связи социально-экономических явлений, выражается функцией
Линейная модель множественной регрессии. Спецификация эконометрической модели. Отбор факторов, включаемых в модели множественной регрессии. Фиктивные переменные. Линейное уравнение множественной регрессии.
Построение модели множественной регрессии является одним из методов характеристики аналитической формы связи между зависимой (результативной) переменной и несколькими независимыми (факторными) переменными.
Модель множественной регрессии строится в том случае, если коэффициент множественной корреляции показал наличие связи между исследуемыми переменными.
Общий вид линейной модели множественной регрессии:
где yi – значение i-ой результативной переменной,
x1i…xmi – значения факторных переменных;
– неизвестные коэффициенты модели множественной регрессии;
– случайные ошибки модели множественной регрессии.
При построении нормальной линейной модели множественной регрессии учитываются пять условий:
1) факторные переменные x1i…xmi – неслучайные или детерминированные величины, которые не зависят от распределения случайной ошибки модели регрессии
2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:
3) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:
4) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т.е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):
Это условие выполняется в том случае, если исходные данные не являются временными рядами;
5) на основании третьего и четвёртого условий часто добавляется пятое условие, заключающееся в том, что случайная ошибка модели регрессии – это случайная величина, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2:
Общий вид нормальной линейной модели парной регрессии в матричной форме:
– случайный вектор-столбец значений результативной переменной размерности (n*1);
– матрица значений факторной переменной размерности (n*(m+1)). Первый столбец является единичным, потому что в модели регрессии коэффициент умножается на единицу;
– вектор-столбец неизвестных коэффициентов модели регрессии размерности ((m+1)*1);
– случайный вектор-столбец ошибок модели регрессии размерности (n*1).
Включение в линейную модель множественной регрессии случайного вектора-столбца ошибок модели обусловлено тем, что практически невозможно оценить связь между переменными со 100-процентной точностью.
Условия построения нормальной линейной модели множественной регрессии, записанные в матричной форме:
1) факторные переменные x1j…xmj – неслучайные или детерминированные величины, которые не зависят от распределения случайной ошибки модели регрессии . В терминах матричной записи Х называется детерминированной матрицей ранга (k+1), т.е. столбцы матрицы X линейно независимы между собой и ранг матрицы Х равен m+1
2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:
3) предположения о том, что дисперсия случайной ошибки модели регрессии является постоянной для всех наблюдений и ковариация случайных ошибок любых двух разных наблюдений равна нулю, записываются с помощью ковариационной матрицы случайных ошибок нормальной линейной модели множественной регрессии:
In – единичная матрица размерности (n*n).
4) Х случайной величиной, подчиняющейся многомерному нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2:
В нормальную линейную модель множественной регрессии должны входить факторные переменные, удовлетворяющие следующим условиям:
1) данные переменные должны быть количественно измеримыми;
2) каждая факторная переменная должна достаточно тесно коррелировать с результативной переменной;
3) факторные переменные не должны сильно коррелировать друг с другом или находиться в строгой функциональной зависимости.
Определение явного вида эконометрической модели называется спецификацией эконометрической модели.
При спецификации эконометрических моделей принято учитывать четыре принципа:
1) эконометрические утверждения и закономерности должны быть переведены на математический язык;
2) количество уравнений в модели должно быть равно числу эндогенных переменных;
3) переменные должны быть датированы;
4) в модель должен быть включён параметр случайной ошибки, чтобы охарактеризовать влияние случайных факторов.
Существуют следующие формы спецификации моделей:
1) структурная форма модели, когда эндогенные переменные не выражены явно через предопределенные переменные;
2) приведенная форма модели, когда эндогенные переменные представляют собой явно выраженные функции от предопределенных переменных.
Экономическим объектом в эконометрической модели Самуэльсона-Хикса является закрытая экономика.
Состояние закрытой экономики в текущем периоде t характеризуется переменными (Yt, Ct, It, Gt),
где Yt – валовой внутренний продукт (ВВП);
Ct – уровень потребления;
It – величина инвестиций;
Gt – государственные расходы.
При составлении спецификации модели Самуэльса-Хикса необходимо учесть следующие экономические утверждения:
1) текущее потребление объясняется уровнем валового внутреннего продукта в предыдущем периоде, увеличиваясь одновременно с ним, но с меньшей скоростью;
2) величина инвестиций прямо пропорциональна приросту валового внутреннего продукта за предшествующий период (прирост ВВП за предшествующий период определяется как разность Yt-lи Yt-2);
3) государственные расходы возрастают с постоянным темпом роста;
4) текущее значение валового внутреннего продукта представляет собой сумму текущих уровней потребления, инвестиций и государственных расходов (тождество системы национальных счетов).
Если вышеперечисленные экономические утверждения перевести на математический язык, то мы придём к спецификации модели вида (1):
Спецификация (1) модели близка к приведённой форме: текущие переменные Ct, It и Gt являются явными функциями предопределен–ных переменных, а переменную Yt можно сделать явной функцией путём подстановки правых частей первых трёх уравнений в правую часть четвёртого уравнения.
В итоге получим приведённую форму (2) модели Самуэльсона-Хикса:
Основное отличие эконометрических моделей от других видов моделей заключается в обязательном включении в модель случайной ошибки.
Случайная ошибка характеризуется следующими свойствами:
1) математическое ожидание случайной ошибки при всех значениях эндогенной переменной равно нулю;
2) дисперсии случайной ошибки удовлетворяют свойству гомоскедастичности, т. е. постоянства дисперсий.
Запишем спецификацию модели вида (1) с учётом случайной ошибки:
С учётом первой и третьей спецификаций модели Самэльсона-Хикса, получим приведённую форму данной модели (4):
Наиболее часто применяются два метод отбора факторов:
1. Метод исключения предполагает построение модели, включающей всю совокупность факторов, с последующим сокращением их числа до тех пор, пока все коэффициенты при факторах не будут иметь t-статистики, превышающие по модулю единицу. На каждом шаге исключается тот фактор, коэффициент при котором незначим и имеет наименьшую t-статистику.
2. Метод включения состоит в последовательном добавлении в модель факторов до тех пор, пока скорректированный коэффициент детерминации не перестанет увеличиваться. Первыми в модель включаются факторы, имеющие больший парный коэффициент корреляции с результатом Y.
Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлениями исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями.
К факторам, включаемым в модель, предъявляются следующие требования:
1. Факторы должны быть количественно измеримы.Включение фактора в модель должно приводить к существенному увеличению доли объясненной части в общей вариации зависимой переменной. Поскольку данная величина характеризуетсякоэффициентом детерминации, включение нового фактора в модель должно приводить к заметному изменению коэффициента. Если этого не происходит, то включаемый в анализ фактор не улучшает модель и является лишним.
Например, если для регрессии, включающей 5 факторов, коэффициент детерминации составил 0,85, и включение шестого фактора дало коэффициент детерминации 0,86, то вряд ли целесообразно дополнять модель этим фактором.
Если необходимо включить в модель качественный фактор, не имеющий количественной оценки, то нужно придать ему количественную определенность. В этом случае в модель включается соответствующая ему «фиктивная» переменная, имеющая конечное количество формально численных значений, соответствующих градациям качественного фактора (балл, ранг).
Например, если нужно учесть влияние уровня образования (на размер заработной платы), то в уравнение регрессии можно включить переменную, принимающую значения: 0 – при начальном образовании, 1 – при среднем, 2 – при высшем.
Несмотря на то, что теоретически регрессионная модель позволяет учесть любое количество факторов, на практике в этом нет необходимости, т.к. неоправданное их увеличение приводит к затруднениям в интерпретации модели и снижению достоверности результатов.
2. Факторы не должны быть взаимно коррелированыи, тем более, находиться в точной функциональной связи. Наличие высокой степени коррелированности между факторами может привести к неустойчивости и ненадежности оценок коэффициентов регрессии, а также к невозможности выделить изолированное влияние факторов на результативный показатель. В результате параметры регрессии оказываются неинтерпретируемыми.
До сих пор в качестве факторов рассматривались экономические переменные, принимающие количественные значения в некотором интервале. Вместе с тем может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Это могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону. Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т.е. качественные переменные преобразованы в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными.
Исследование зависимости заработной платы от наличия у работника высшего образования.
В дополнение к этим переменным введем фиктивную булеву переменную z:
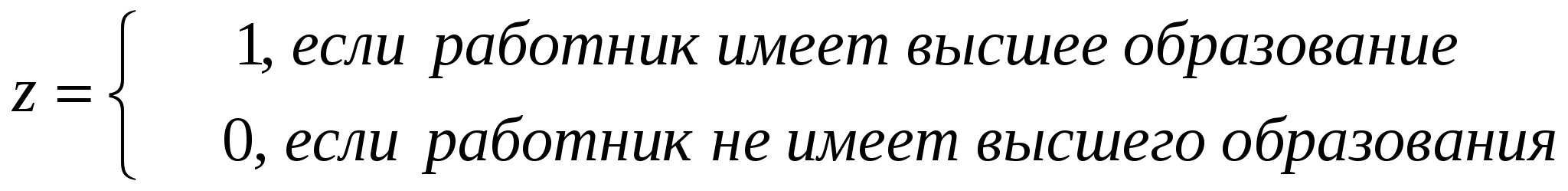
Тогда уравнение регрессии будет иметь вид:
По статистическим данным, используя метод наименьших квадратов, мы получим оценки, в том числе и параметра 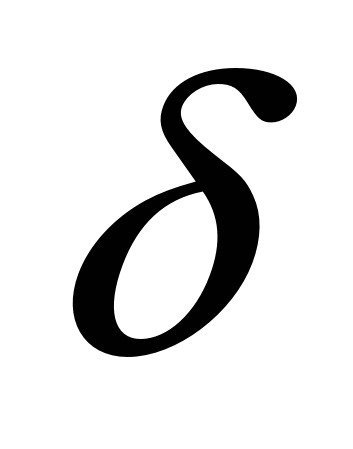
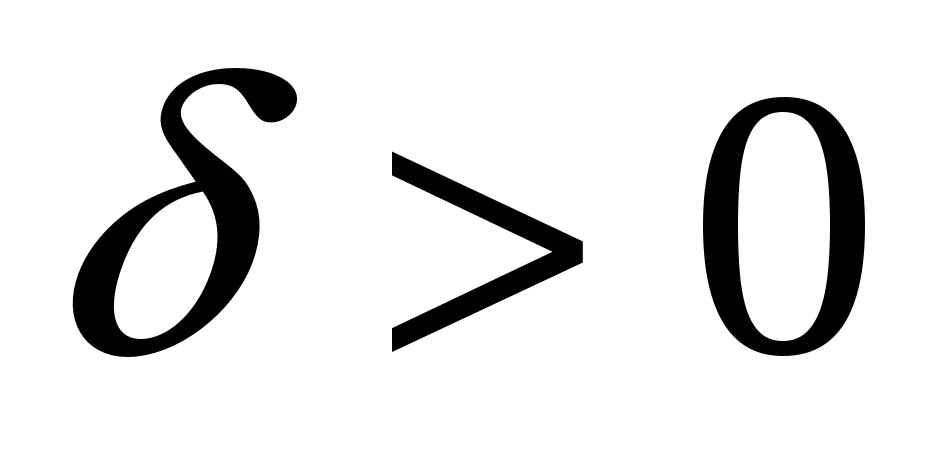
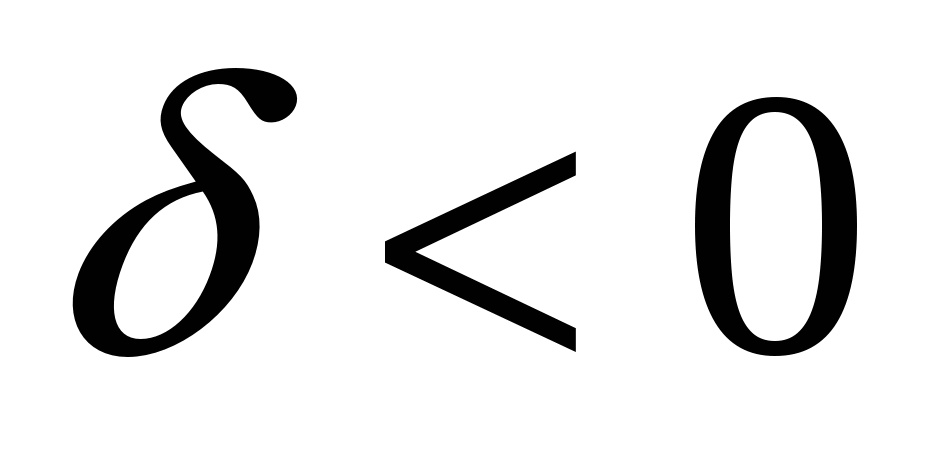
Задачей множественной линейной регрессии является построение линейной модели связи между набором непрерывных предикторов и непрерывной зависимой переменной. Часто используется следующее регрессионное уравнение:
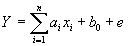
Здесь аi — регрессионные коэффициенты, b0 — свободный член(если он используется), е — член, содержащий ошибку — по поводу него делаются различные предположения, которые, однако, чаще сводятся к нормальности распределения с нулевым вектором мат. ожидания и корреляционной матрицей 
Такой линейной моделью хорошо описываются многие задачи в различных предметных областях, например, экономике, промышленности, медицине. Это происходит потому, что некоторые задачи линейны по своей природе.
Приведем простой пример. Пусть требуется предсказать стоимость прокладки дороги по известным ее параметрам. При этом у нас есть данные о уже проложенных дорогах с указанием протяженности, глубины обсыпки, количества рабочего материала, числе рабочих и так далее.
Ясно, что стоимость дороги в итоге станет равной сумме стоимостей всех этих факторов в отдельности. Потребуется некоторое количество, например, щебня, с известной стоимостью за тонну, некоторое количество асфальта также с известной стоимостью.
Возможно, для прокладки придется вырубать лес, что также приведет к дополнительным затратам. Все это вместе даст стоимость создания дороги.
При этом в модель войдет свободный член, который, например, будет отвечать за организационные расходы (которые примерно одинаковы для всех строительно-монтажных работ данного уровня) или налоговые отчисления.
Ошибка будет включать в себя факторы, которые мы не учли при построении модели (например, погоду при строительстве — ее вообще учесть невозможно).
Уравнение множественной регрессии может быть представлено в виде:
где X = X(X1, X2, . Xm) — вектор независимых (объясняющих) переменных; β — вектор параметров (подлежащих определению); ε — случайная ошибка (отклонение); Y — зависимая (объясняемая) переменная.
теоретическое линейное уравнение множественной регрессии имеет вид:
β0 — свободный член, определяющий значение Y, в случае, когда все объясняющие переменные Xj равны 0.
Метод наименьших квадратов (МНК). Оценка параметров линейных уравнений регрессии. Предпосылки МНК, методы их проверки. Свойства оценок параметров эконометрической модели, получаемых при помощи МНК.
Метод наименьших квадратов (МНК) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.
Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Для линейных уравнений регрессии (и нелинейных уравнений, приводимых к линейным) строится система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии. В случае линейной множественной регрессии y = a + b • x + b • x0 +. + b • x
система нормальных уравнений имеет следующий вид:
Z y=п •a+ь Z xi+Ь2 Z X2 +. +bp Z xp; Z yxi = aZ xi+bi Zx2+b2 Z x2 xi +. +bp Z xpxi;
Z yxp = aZ xp+bi Z xi xP+b2 Z x2 xP+. +bp Z x?.
Для определения значимости факторов и повышения точности результата используется уравнение множественной регрессии в стандартизованном масштабе
‘y=b • tx,+b • fx, +. +bp • t4 (?.3)
где ty, tx . tx — стандартизованные переменные
для которых среднее значение равно нулю ty = tx = 0, а среднее квадратичес- кое отклонение равно единице s = s = 1.
Величины в; называются стандартизованными коэффициентами регрессии.
К уравнению множественной регрессии в стандартизованном масштабе применим МНК. Стандартизованные коэффициенты регрессии (в-коэффициенты) определяются из следующей системы уравнений:
Z % =b Z +b Z ‘x, +b Z ‘з +. +bP Z 4 ;
Z tytXl =bi Z tx, tx, + b Z ‘1 +b Z tx, tx3 +. + bP Z tx, txp;
2Z ‘y’xp =b Z ‘xi ‘xp +b2 Z ‘x, ‘xp +b Z ‘x3 ‘xp + . + bp Z ‘
либо из системы уравнений
ryx, = Pi + Arx,x + brx3xi + . + ;
ryx, = birxix2 + p2 + p3rx3x, + . + Pprxpx, ;
ryxp =birxixp +P2 rx, xp +P3 rx3xp + . + bp .
Стандартизованные коэффициенты регрессии показывают, на сколько сигм (средних квадратических отклонений) изменится в среднем результат, если со-ответствующий фактор х изменится на одну сигму при неизменном среднем уровне других факторов. В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии сравнимы между собой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые несравнимы между собой.
В парной зависимости стандартизованный коэффициент регрессии в есть не что иное, как линейный коэффициент корреляции гух.
Связь коэффициентов множественной регрессии bi со стандартизованными коэффициентами в і описывается соотношением ?
Параметр а определяется из соотношения a = у — b1 x1 — b2 x2 -. — bpxp.
При оценке параметров уравнения регрессии применяется МНК. При этом делаются определенные предпосылки относительно составляющей 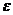
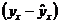
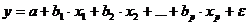
Исследования остатков 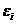
1) случайный характер остатков. С этой целью строится график отклонения остатков от теоретических значений признака. Если на графике получена горизонтальная полоса, то остатки представляют собой случайные величины и применение МНК оправдано. В других случаях необходимо применить либо другую функцию, либо вводить дополнительную информацию и заново строить уравнение регрессии до тех пор, пока остатки не будут случайными величинами.
2) нулевая средняя величина остатков, т.е. 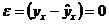
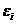
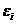
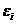
3. Гомоскедастичность — дисперсия каждого отклонения 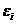
4. Отсутствие автокорреляции остатков. Значения остатков 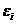
5. Остатки подчиняются нормальному распределению.
В тех случаях, когда все пять предпосылок выполняются, оценки, полученные по МНК и методу максимального правдоподобия, совпадают между собой. Если распределение случайных остатков 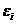
Метод наименьших квадратов (МНК), при котором рассчитывается сумма квадратов отклонений наблюдаемых значений результативной переменной 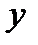
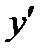
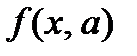
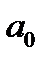
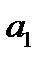
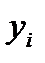
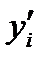
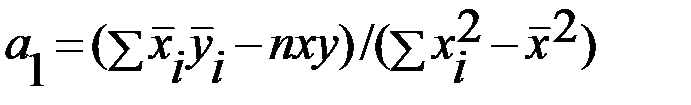
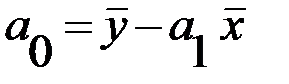
Достоинства МНК: сведение всех вычислительных процедур к простому вычислению неизвестных коэффициентов; доступность математических выводов.
Недостатки МНК: чувствительность оценок к резким выбросам, встречающимся в исходных данных. Метод наименьших квадратов является наиболее распространенным методом оценки неизвестных параметров модели парной линейной регрессии.
Тема 11 Причинность, регрессия, корреляция
Причинность, регрессия, корреляция
Исследование объективно существующих связей между социально-экономическими явлениями и процессами является важнейшей задачей теории статистики. В процессе статистического исследования зависимостей вскрываются причинно-следственные отношения между явлениями, что позволяет выявлять факторы (признаки), оказывающие основное влияние на вариацию изучаемых явлений и процессов. Причинно-следственные отношения ‑ это такая связь явлений и процессов, когда изменение одного из них ‑ причины ведет к изменению другого ‑ следствия.
Финансово-экономические процессы представляют собой результат одновременного воздействия большого числа причин. Следовательно, при изучении этих процессов необходимо выявлять главные, основные причины, абстрагируясь от второстепенных.
В основе первого этапа статистического изучения связи лежит качественный анализ, связанный с анализом природы социального или экономического явления методами экономической теории, социологии, конкретной экономики.
Второй этап – построение модели связи, базируется на методах статистики: группировках, средних величинах, и так далее.
Третий, последний этап ‑ интерпретация результатов, вновь связан с качественными особенностями изучаемого явления. Статистика разработала множество методов изучения связей. Выбор метода изучения связи зависит от познавательной цели и задач исследования.
Признаки по их сущности и значению для изучения взаимосвязи делятся на два класса.
Признаки, обуславливающие изменения других, связанных с ними признаков, называются факторными, или просто факторами.
Признаки, изменяющиеся под действием факторных признаков, называются результативными.
В статистике различают функциональную и стохастическую зависимости.
Функциональной называют такую связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака.
Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, среднем, при большом числе наблюдений, то такая зависимость называется стохастической. Частным случаем стохастической связи является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков.
Связи между явлениями и их признаками классифицируются по степени тесноты, направлению и аналитическому выражению.
Таблица 11.1. ‑ Количественные критерии оценки тесноты связи
Величина показателя связи
По направлению выделяют связь прямую и обратную.
Прямая ‑ это связь, при которой с увеличением или с уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного признака.
Пример. Так, рост объемов производства способствует увеличению прибыли предприятия.
В случае обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с изменением факторного признака, то есть обратная ‑ это связь, при которой с увеличением или с уменьшением значений одного признака происходит уменьшение или увеличение значений другого признака.
Пример. Так, снижение себестоимости единицы производимой продукции влечет за собой рост рентабельности.
По аналитическому выражению выделяют связи прямолинейные (или просто линейные) и нелинейные.
Если статистическая связь между явлениями может быть приблизительно выражена уравнением прямой линии, то ее называют линейной связью вида:
Если же связь может быть выражена уравнением какой-либо кривой, то такую связь называют нелинейной или криволинейной, например:
Для выявления наличия связи, ее характера и направления в статистике используются методы: приведения параллельных данных; графический; аналитических группировок; корреляции, регрессии.
Метод приведения параллельных данных основан на сопоставлении двух или нескольких рядов статистических величин. Такое сопоставление позволяет установить наличие связи и получить представление о ее характере.
Графически взаимосвязь двух признаков изображается с помощью поля корреляции. В системе координат на оси абсцисс откладываются значения факторного признака, а на оси ординат ‑ результативного. Каждое пересечение линий, проводимых через эти оси, обозначаются точкой. При отсутствии тесных связей имеет место беспорядочное расположение точек на графике. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи.
В статистике принято различать следующие виды зависимостей:
- Парная корреляция ‑ связь между двумя признаками (результативным и факторным, или двумя факторными).
- Частная корреляция ‑ зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков.
- Множественная корреляция ‑ зависимость результативного и двух или более факторных признаков, включенных в исследование.
Корреляционный анализ имеет своей задачей количественное определение тесноты и направления связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи).
Теснота связи количественно выражается величиной коэффициентов корреляции, которые, давая количественную характеристику тесноты связи между признаками, позволяют определять «полезность» факторных признаков при построении уравнения множественной регрессии. Знаки при коэффициентах корреляции характеризуют направление связи между признаками.
Регрессия тесно связана с корреляцией и позволяет исследовать аналитическое выражение взаимосвязи между признаками.
Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины (называемой зависимой или результативным признаком), обусловлено влиянием одной или нескольких независимых величин (факторных признаков).
Одной из проблем построения уравнений регрессии является их размерность, то есть определение числа факторных признаков, включаемых в модель. Их число должно быть оптимальным. Сокращение размерности за счет исключения второстепенных, несущественных факторов позволяет получить модель, быстрее и качественнее реализуемую. В то же время, построение модели малой размерности может привести к тому, что она будет недостаточно полно описывать исследуемое явление или процесс.
При построении моделей регрессии должны соблюдаться требования:
- Совокупность исследуемых исходных данных должна быть однородной и математически описываться непрерывными функциями.
- Возможность описания моделируемого явления одним или несколькими уравнениями причинно-следственных связей.
- Все факторные признаки должны иметь количественное (числовое) выражение.
- Наличие достаточно большого объема исследуемой совокупности (в последующих примерах в целях упрощения изложения материала это условие нарушено, т.е. объем очень мал).
- Причинно-следственные связи между явлениями и процессами должны описываться линейной или приводимой к линейной форме зависимостью.
- Отсутствие количественных ограничений на параметры модели связи.
- Постоянство территориальной и временной структуры изучаемой совокупности.
Соблюдение данных требований позволяет построить модель, наилучшим образом описывающую реальные социально-экономические явления и процессы.
Парная регрессия на основе метода наименьших квадратов позволяет получить аналитическое выражение связи между двумя признаками: результативным и факторным.
Определить тип уравнения можно, исследуя зависимость графически, однако существуют более общие указания, позволяющие выявить уравнение связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково, то это свидетельствует о том, что связь между ними линейная, а при обратной связи ‑ гиперболическая. Если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то используется параболическая или степенная регрессия.
Оценка параметров уравнений регрессии ( и — в уравнении параболы второго порядка) осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности и нахождении параметров модели , при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:
Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид:
где п ‑ объем исследуемой совокупности (число единиц наблюдения).
В уравнениях регрессии параметр ао показывает усредненное влияние на результативный признак неучтенных в уравнении факторных признаков. Коэффициент регрессии а1 показывает, на сколько в среднем изменяется значение результативного признака при увеличении факторного признака на единицу собственного измерения. xi – теоретические значения результативного признака; yi – наблюдаемые значения факторного признака.
Пример. Имеются данные по 10 однотипным предприятиям о выпуске продукции (х) в тыс.ед. и о расходе условного топлива (у) в тоннах (графы 1 и 2 табл. 17).
Требуется найти уравнение зависимости расхода топлива от выпуска продукции (или уравнение регрессии у по х) и измерить тесноту зависимости между ними. Для этого представим данные в табл. 11.2 (вместе с расчетными столбцами).
Таблица 11.2 – Расчет показателей для нахождения уравнения регрессии
| № п/п | Выпуск продукции, xi,тыс.ед. | Расход топлива, yi, тонн |  | |||
| 1 | 5 | 4 | 25 | 20 | 16 | 3,9 |
| 2 | 6 | 4 | 36 | 24 | 16 | 4,4 |
| 3 | 8 | 6 | 64 | 48 | 36 | 5,5 |
| 4 | 8 | 5 | 64 | 40 | 25 | 5,5 |
| 5 | 10 | 7 | 100 | 70 | 49 | 6,6 |
| 6 | 10 | 8 | 100 | 80 | 64 | 6,6 |
| 7 | 14 | 8 | 196 | 112 | 64 | 8,8 |
| 8 | 20 | 10 | 400 | 200 | 100 | 12,1 |
| 9 | 20 | 12 | 400 | 240 | 144 | 12,1 |
| 10 | 24 | 16 | 576 | 384 | 256 | 14,3 |
| ∑ * | 125 | 80 | 1961 | 1218 | 770 | 80 |
Необходимые для решения суммы рассчитаны выше в таблице. Подставим их в уравнение и решим систему.
Получив искомое уравнение регрессии можно утверждать, что с увеличение выпуска продукции на тыс. ед., расход топлива возрастет в среднем на 0,547 тонны.
* Если параметры уравнения найдены верно, то
Измерение тесноты (силы) и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака и одного (при изучении парных зависимостей) или нескольких (множественных зависимостей) факторных признаков.
Линейный коэффициент корреляции (К. Пирсона) характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости.
В теории разработаны и на практике применяются различные модификации формулы расчета данного коэффициента.
Для измерения тесноты зависимости между у и х применяют линейный коэффициент корреляции, который может быть рассчитан по любой из нижеприведенных формул:
Таблица 11.3 – Оценка линейного коэффициента корреляции
| Значение линейного коэффициента связи | Характеристика связи | Интерпретация связи |
| г = 0 | отсутствует | – |
| 0 Линейный коэффициент корреляции может принимать по модулю значения от 0 до 1 (знак + при прямой зависимости и знак – при обратной зависимости). Найденный коэффициент корреляции По степени тесноты связи между признаками (одним из критериев оценки служит коэффициент корреляции) различают связи: Следовательно, 0,7≤0,96≤ 1 , значит, связь в данном примере сильная (с увеличением выпуска продукции увеличивается расход топлива). Термин “корреляция” впервые применил французский палеонтолог Ж. Кювье, который вывел “закон корреляции частей и органов животных” (этот закон позволяет восстанавливать по найденным частям тела облик всего животного). В статистику указанный термин ввел в 1886 году английский биолог и статистик Френсис Гальтон (не просто связь – relation, а “как бы связь” – co-relation). Однако точную формулу для подсчёта коэффициента корреляции разработал его ученик – математик и биолог – Карл Пирсон (1857 – 1936). Корреляционным называется исследование, проводимое для подтверждения или опровержения гипотезы о статистической связи между несколькими (двумя и более) переменными. В психологии переменными могут выступать психические свойства, процессы, состояния и др. Контрольные задания. По данным статистических сборников постройте таблицу: по 10 однотипным предприятиям с данными о численности персонала, выпуске продукции, расходах; данных о прожиточном минимуме и средней заработной плате и т.п.; найдите уравнение зависимости (или уравнение регрессии) и измерьте тесноту связи между показателями. Корреляция и регрессияКогда вы исследуете закономерности в своих данных, как вы можете определить, насколько тесно связаны между собой две переменные? Можете ли вы использовать одну переменную для предсказания другой? В этом модуле вы познакомитесь с концепциями корреляции и регрессии, которые могут помочь вам в дальнейшем изучении, понимании и обмене данными. ЦелиПо завершении этого модуля вы сможете:
Раздел 1. КорреляцияВ этом модуле вы познакомитесь с двумя концепциями, которые помогут вам в изучении взаимосвязей между переменными: корреляция и регрессия. Начнем с корреляции. Что такое корреляция?Корреляция – это техника, которая может показать, насколько сильно связаны пары количественных переменных. Например, количество ежедневно потребляемых калорий и масса тела взаимосвязаны, но эта связь не абсолютная. Многие из нас знают кого-то, кто очень худой, несмотря на то, что он/она регулярно потребляет большое количество калорий, и мы также знаем кого-то, у кого есть проблемы с лишним весом, даже когда он/она сидит на диете с пониженным содержанием калорий. Однако средний вес людей, потребляющих 2000 калорий в день, будет меньшим, чем средний вес людей, потребляющих 2500, а их средний вес будет еще меньше, чем у людей, потребляющих 3000, и так далее. Корреляция может сказать вам, насколько тесно разница в весе людей связана с количеством потребляемых калорий. Корреляция между весом и потреблением калорий – это простой пример, но иногда данные, с которыми вы работаете, могут содержать корреляции, которых вы никак не ожидаете. А иногда вы можете подозревать корреляции, не зная, какие из них самые сильные. Корреляционный анализ помогает лучше понять связи в ваших данных. Диаграммы разброса или Точечные диаграммы используются для графического представления взаимосвязей между количественными показателями. Диаграмма показывает данные и позволяет нам проверить свои предположения, прежде чем устанавливать корреляции. Глядя на взаимосвязь между продажами и маркетингом, можно предположить наличие в них корреляции. По мере того, как одна переменная растет, другая, похоже, тоже увеличивается. Диаграмма, указывающая на корреляцию между двумя количественными переменными Корреляция против причинно-следственной связиТеперь вы знаете, как определяется корреляция и как ее можно представить графически. Теперь давайте посмотрим, как понимать корреляцию. Во-первых, важно понимать, что корреляция никогда не доказывает наличие причинно-следственной связи. Корреляция говорит нам только о том, насколько сильно пара количественных переменных линейно связана. Она не объясняет, как и почему. Например, продажи кондиционеров коррелируют с продажами солнцезащитных кремов. Люди покупают кондиционеры, потому что они купили солнцезащитный крем, или наоборот? Нет. Причина обеих покупок явно в чем-то другом, в данном случае – в жаркой погоде. Измерение корреляцииКорреляция Пирсона, также называемая коэффициентом корреляции, используется для измерения силы и направления (положительного или отрицательного) линейной связи между двумя количественными переменными. Когда корреляция измеряется в выборке данных, используется буква r. Критерий Пирсона r может находиться в диапазоне от –1 до 1. Когда r = 1, существует идеальная положительная линейная связь между переменными, это означает, что обе переменные идеально коррелируют с увеличением значений. Когда r = –1, существует идеальная отрицательная линейная связь между переменными, это означает, что обе переменные идеально коррелируют при уменьшении значений. Когда r = 0, линейная связь между переменными не наблюдается. На графиках разброса ниже показаны корреляции, где r = 1, r = –1 и r = 0. Переверните каждую карту ниже, чтобы увидеть значение для этой совокупности. Идеальная положительная корреляция Когда r = 1, есть идеальная положительная линейная связь между переменными, и это означает, что обе переменные идеально коррелируют с увеличением значений. Идеальная отрицательная корреляция Когда r = –1, существует идеальная отрицательная линейная связь между переменными, и это означает, что обе переменные идеально коррелируют при уменьшении значений. Нет линейной корреляции Когда r = 0, линейная зависимость между переменными не наблюдается. С реальными данными вы никогда не увидите значений r «–1», «0» или «1». Как правило, чем ближе r к 1 или –1, тем сильнее корреляция, это показано в следующей таблице. r = Сила корреляции От 0.90 до 1 Очень сильная корреляция От 0.70 до 0.89 От 0.40 до 0.69 От 0.20 до 0.39 От 0 to 0.19 Очень слабая корреляция или ее нет вообще Условие корреляцииЧтобы корреляции были значимыми, они должны использовать количественные переменные, и описывать линейные отношения, при этом не может быть выбросов. В 1973 году статистик по имени Фрэнсис Анскомб разработал показатель «квартет Анскомба», он показывает важность визуального представления данных в виде графиков, а не простого выполнения статистических тестов. Выделенный график разброса в верхнем левом углу – единственный, который удовлетворяет условиям корреляции. Четыре визуализации в его квартете показывают одну и ту же линию тренда, поэтому значение r будет одинаковым для всех четырех. Что вы заметили? Только один из графиков рассеяния соответствует критериям линейности и отсутствия выбросов. Другими словами, мы не должны проводить корреляции на трех из четырех примерах, потому что не имеет смысла устанавливать сильные отношения. Проверка знанийСилу корреляции при значении r, равному –0,52, лучше всего можно описать как:
РезюмеИтак, вы ознакомились с концепциями статистической техники корреляции. На следующем уроке вы узнаете о линейной регрессии. Раздел 2. Линейная регрессияНа предыдущем уроке вы узнали, что корреляция относится к направлению (положительному или отрицательному) и силе связи (от очень сильной до очень слабой) между двумя количественными переменными. Линейная регрессия также показывает направление и силу взаимосвязи между двумя числовыми переменными, но регрессия использует наиболее подходящую прямую линию, проходящую через точки на диаграмме рассеяния, чтобы предсказать, как X вызывает изменение Y. При корреляции значения X и Y взаимозаменяемы. При регрессии результаты анализа изменятся, если поменять местами X и Y. Диаграмма рассеяния с линией регрессии Линия регрессииКак и в случае с корреляциями, для того, чтобы регрессии были значимыми, они должны:
Как и корреляция, линейная регрессия отображается на диаграмме рассеяния Линия регрессии на диаграмме рассеяния – это наиболее подходящая прямая линия, которая проходит через точки на диаграмме рассеяния. Другими словами, это линия, которая проходит через точки с наименьшим расстоянием от каждой из них до линии (поэтому в некоторых учебниках вы можете встретить название «регрессия наименьших квадратов»). Почему эта линия так полезна? Мы можем использовать вычисление линейной регрессии для вычисления или прогнозирования нашего значения Y, если у нас есть известное значение X. Чтобы было понятнее, давайте рассмотрим пример. Пример регрессииПредставьте, что вы хотите предсказать, сколько вам нужно будет заплатить, чтобы купить дом площадью 1,500 квадратных футов. Давайте используем для этого линейную регрессию.
Вот диаграмма рассеяния, показывающая цены на жилье (ось Y) и площадь в квадратных футах (ось x). Вы можете видеть, что дома с большим количеством квадратных футов, как правило, стоят дороже, но сколько именно вам придется потратить на дом размером 1500 квадратных футов? Диаграмма рассеяния цен на дома и квадратных метров Чтобы помочь вам ответить на этот вопрос, проведите линию через точки. Это и будет линия регрессии. Линия регрессии поможет вам предсказать, сколько будет стоить типовой дом определенной площади в квадратных метрах. В этом примере вы можете видеть уравнение для линии регрессии. Уравнение линии регрессииУравнение линии регрессии: Y = 113x + 98,653 (с округлением). Что означает это уравнение? Если вы купили просто место без площади (пустой участок), цена составит 98,653 доллара. Вот как можно решить это уравнение: Чтобы найти Y, умножьте значение X на 113, а затем добавьте 98,653. В этом случае мы не смотрим на квадратные метры, поэтому значение X равно «0».
Значение 98,653 называется точкой пересечения по оси Y, потому что здесь линия пересекает ось Y. Это – значение Y, когда X равно «0». Но что такое 113? Число «113» – это наклон линии. Наклон – это число, которое описывает как направление, так и крутизну линии. В этом случае наклон говорит нам, что за каждый квадратный фут цена дома будет расти на 113 долларов. Итак, сколько вам нужно будет потратить на дом площадью 1500 квадратных футов? Y = (113 * 1500) + 98,653 = $268,153 Взгляните еще раз на эту диаграмму рассеяния. Синие отметки – это фактические данные. Вы можете видеть, что у вас есть данные для домов площадью от 1100 до 2450 квадратных футов. Насколько можно быть уверенным в результате, используя приведенное выше уравнение, чтобы спрогнозировать цену дома площадью в 500 квадратных футов? Насколько можно быть уверенным в результате, используя приведенное выше уравнение, чтобы предсказать цену дома площадью 10,000 квадратных футов? Поскольку оба этих измерения находятся за пределами диапазона фактических данных, вам следует быть осторожными при прогнозировании этих значений. Величина достоверности аппроксимацииНаведите курсор на линию регрессии, чтобы увидеть значение величины достоверности аппроксимации r. В дополнение к уравнению в этом примере мы также видим значение величины достоверности аппроксимации r (также известная как коэффициент детерминации). Это значение является статистической мерой того, насколько близки данные к линии регрессии или насколько хорошо модель соответствует вашим наблюдениям. Если данные находятся точно на линии, значение величины достоверности аппроксимации будет 1 или 100%, и это означает, что ваша модель идеально подходит (все наблюдаемые точки данных находятся на линии). Для наших данных о ценах на жилье значение величины достоверности аппроксимации составляет 0,70, или 70%. Корреляция против причинно-следственной связиТеперь давайте рассмотрим, как отличить линейную регрессию от корреляции. Линейная регрессия
Корреляция
Готовы проверить свои знания? В следующем упражнении определите, чему соответствует каждое из описаний: корреляции или регрессии. Варианты для категорий: «корреляция» или «регрессия». Измеряется величиной достоверности аппроксимации Прогнозирует значения Y на основе значений X. Не предсказывает значения Y из значений X, только показывает взаимосвязь. Переменные оси X и Y взаимозаменяемы. Если поменять местами X и Y, результаты анализа изменятся. РезюмеИтак, здесь вы познакомились со статистическими концепциями корреляции и регрессии. Это поможет вам лучше исследовать и понимать данные, с которыми вы работаете, путем изучения взаимосвязей в них. источники: http://stat-ist.ru/statistika-kurs-lektsij/korrelyatsiya-prichinnost-regressiya http://biconsult.ru/services/korrelyaciya-i-regressiya |
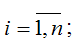
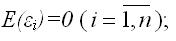
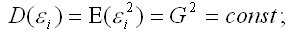
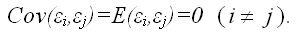
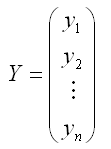

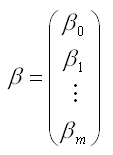
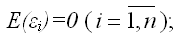
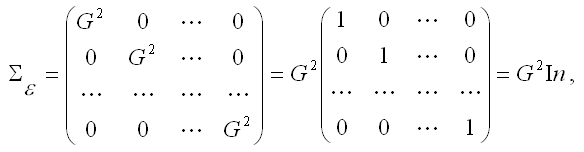
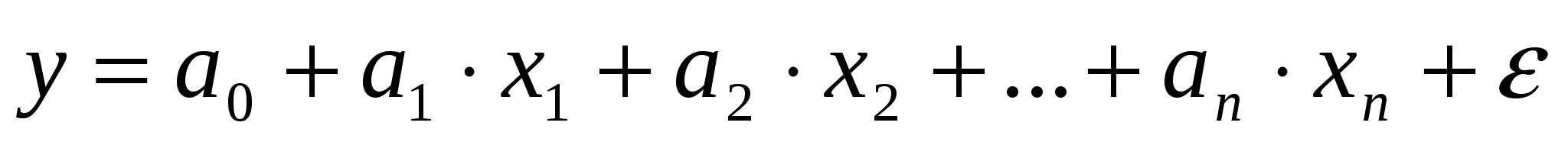
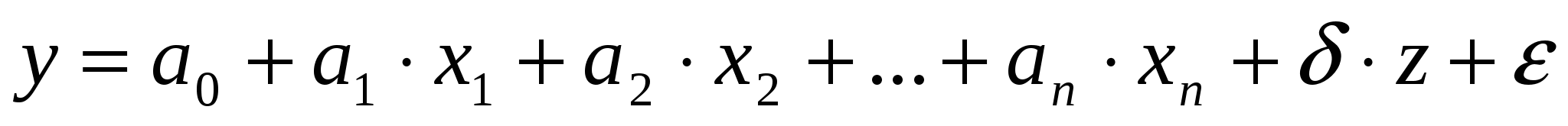

















 означает, что характер связи между исследуемыми признаками прямой.
означает, что характер связи между исследуемыми признаками прямой.