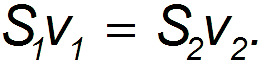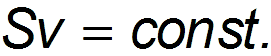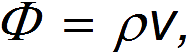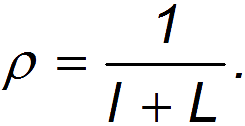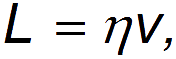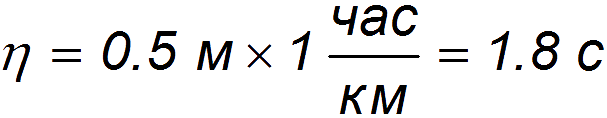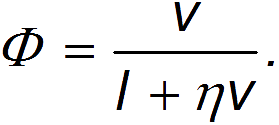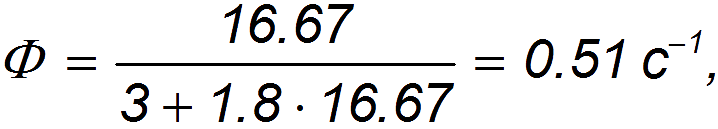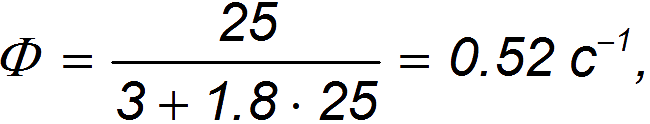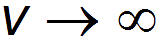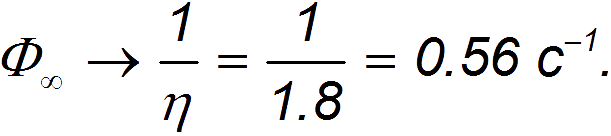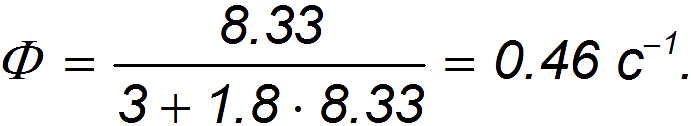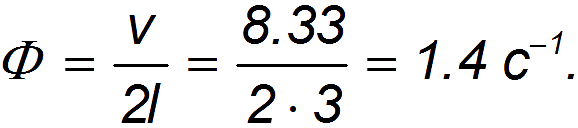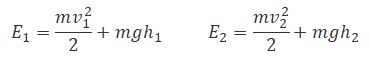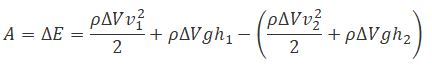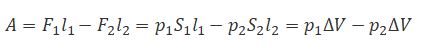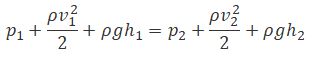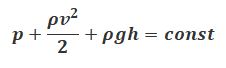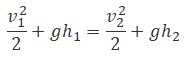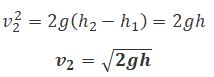Стационарное течение несжимаемой жидкости описывает уравнение

§ 9.9. Кинематическое описание движения жидкости

Стационарное движение жидкости. Трубки тока

Скорости элементов жидкости в различных точках пространства, вообще говоря, различны. Если во всех точках пространства скорости элементов жидкости не меняются со временем, то движение жидкости называется стационарным (установившимся). При стационарном течении любая частица жидкости проходит данную точку с одним и тем же значением скорости v. В другой какой-либо точке скорость частицы будет иной, но также постоянной во времени.

Картина линий тока при стационарном течении остается неизменной. Линии тока в этом случае совпадают с траекториями частиц.

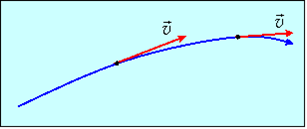
Объем жидкости, ограниченный линиями тока, называется трубкой тока (рис. 9.37). Скорости элементов жидкости в каждой точке поверхности трубки тока направлены по касательной к этой поверхности. Поэтому частицы при своем движении не пересекают стенок трубки тока. При исследовании течения жидкости вместо реальных труб можно рассматривать трубки тока.

Уравнение неразрывности для несжимаемой жидкости

Разобьем жидкость, текущую по трубе переменного сечения, на отдельные трубки тока, настолько тонкие, что в каждом сечении скорости элементов жидкости можно считать одинаковыми.

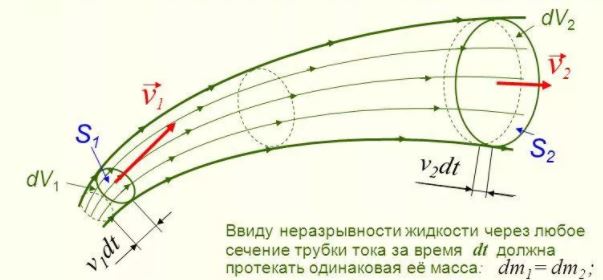
Рассмотрим два сечения трубки тока с площадями S₁ и S₂ (рис. 9.38). Обозначим через ₁ и ₂ соответствующие скорости течения жидкости.

За малое время Δt через первое сечение проходит жидкость, масса которой равна ρ₁S₁v₁Δt, а через второе — ρ₂S₂v₂Δt. Здесь ρ₁ и ρ₂ — плотности жидкости в первом и втором сечениях. Для несжимаемой жидкости ρ₁ = ρ₂ и объем жидкости, прошедшей через первое сечение, равен объему жидкости, протекающей через второе сечение:

ведь жидкость не пересекает стенок трубки тока и не может в ней накапливаться вследствие несжимаемости.

Разделив обе части равенства (9.9.1) на Δt, получим:

Результат можно сформулировать так: модули скоростей несжимаемой жидкости в двух сечениях трубки тока обратно пропорциональны площадям сечений. Соотношение (9.9.2) представляет собой уравнение неразрывности несжимаемой жидкости. Оно справедливо как для стационарного течения, так и для нестационарного.

Согласно уравнению неразрывности скорость жидкости в узких местах трубки больше, чем в широких.

Наш результат справедлив непосредственно для узких трубок тока. Однако если скорости при переходе от одной трубки тока к другой вдоль одного и того же сечения потока (например, в трубке с твердыми стенками) меняются не очень значительно, то уравнение неразрывности можно приближенно применять и для течения всей жидкости. В этом случае под ₁ и ₂ следует понимать средние по сечениям скорости жидкости.

Если при течении жидкости сжимаемостью жидкости можно пренебречь, то справедливо уравнение неразрывности.

9.2. Уравнение непрерывности

Рассмотрим теперь движение жидкости. Самый простой случай — так называемое стационарное течение. Нет никакого противоречия в употреблении слова «стационарный» рядом со словом «течение», которое подразумевает движение элементов жидкости.

Стационарное течение — это течение, при котором скорость жидкости в каждой данной точке остается постоянной как по величине, так и по направлению.

Элементы жидкости приходят и уходят, но в данной точке каждый вновь пришедший элемент приобретает ту скорость, которая этой точке соответствует. Поэтому стационарное течение можно характеризовать полем скоростей, задавая векторную функцию v(r) от пространственных координат. Графически поле скоростей изображается с помощью линий тока.

Ориентированная линия, касательная к которой в каждой точке совпадает по направлению с вектором скорости в данной точке пространства, называется линией тока.

На рис. 9.9 показана линия тока в области течения жидкости.

Рис. 9.9. Линия тока

Если вспомнить то, что мы знаем из школьного курса физики об электричестве, то можно сказать, что линии тока — это аналог силовых линий.

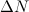
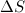
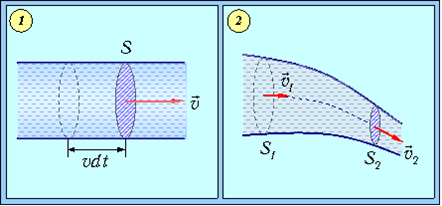
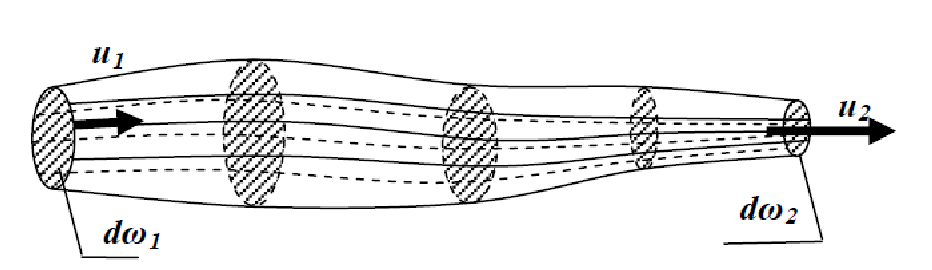
Условимся проводить линии тока так, чтобы густота их (которая характеризуется отношением числа линий к величине перпендикулярной к ним площади , через которую они проходят) была пропорциональна величине скорости в данном месте. Часть жидкости, ограниченную линиями тока, называют трубкой тока. Для стационарного течения форма и расположение линий тока со временем не изменяются.

Рассмотрим какую-либо трубку тока. Всюду далее полагаем площадь сечения трубки достаточно малой, так что можно считать скорость жидкости одинаковой во всех точках сечения. За время dt через произвольное её сечение S проходит объём жидкости Svdt (рис. 9.10–1).

Рис. 9.10 Трубки тока

Выберем два её сечения S₁ и S₂ (рис. 9–2). За время dt через сечение S₁ пройдет объём жидкости S₁v₁dt, где v₁ — скорость течения жидкости в точках сечения S₁. Аналогично, через сечение S₂ за то же время dt пройдёт объём жидкости S₂v₂dt, где v₂ — скорость течения жидкости в точках сечения S₂. Из условия несжимаемости жидкости следует равенство объёмов жидкости, вошедших в область между сечениями S₁, S₂ и вышедших из него:

В несжимаемой жидкости величина Sv в любом сечении одной и той же трубки одинакова,другими словами,эта величина постоянна вдоль трубки тока:

Это соотношение — одна из форм теоремы о непрерывности струи. Данная теорема выражает собой факт несжимаемости жидкости.

Рис. 9.11. Скорость струи в различных сечениях трубки

Теорема о непрерывности струи применима к реальным жидкостям, а также к газам, в том случае, если сжимаемостью их можно пренебречь. Прямое следствие теоремы — широко известный факт: в месте сужения трубы скорость потока возрастает. Более того, аналогичная теорема есть и в теории электромагнетизма, и там она связана с сохранением электрического заряда.

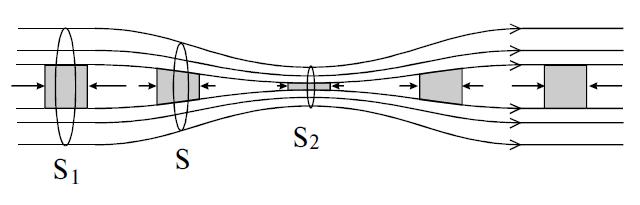
Пример. Оценим пропускную способность одного ряда участка автомагистрали. Учтём, что «Правила дорожного движения» рекомендуют держать дистанцию L между автомобилями, которая в метрах численно равна половине скорости движения, выраженной в км/час.

В этой задаче мы в сущности тоже имеем дело с уравнением непрерывности — при отсутствии «пробки» на дороге через каждое её сечение должно проходить одинаковое количество автомобилей. Поток автомобилей равен

где v — средняя скорость движения, а ρ — линейная «плотность» автомобилей на дороге, то есть число машин на единицу длины. Если l — средняя длина автомобиля, a L — средняя дистанция между ними, то

Рекомендацию «Правил дорожного движения» математически можно выразить в виде формулы:

— «коэффициент безопасности». В итоге приходим к выражению:

Для численной оценки примем l = 3 м, a v = 60 км/час = 16,67 м/с (допустимая скорость движения в городах). Получаем тогда:

то есть каждый ряд способен пропустить 30 машин в минуту.

При повышении скорости движения до v = 90 км/час = 25 м/с пропускная способность возрастает совершенно незначительно: в этом случае находим

Даже в пределе бесконечно большой скорости движения

предельное значение потока

При снижении скорости движения, скажем, до v = 30 км/час = 8,33 м/с пропускная способность станет

Гораздо более «эффективным» является несоблюдение дистанции. Скажем, при дистанции L, равной длине l корпуса автомобиля, и скорости движения v = 30 км/час, получаем для потока:

Но вряд ли повышение пропускной способности магистрали даже в три раза должно достигаться за счет уменьшения безопасности движения.

Стационарное течение несжимаемой жидкости описывает уравнение

Гидродинамика — раздел физики сплошных сред, изучающий движение идеальных и реальных жидкости и газа.

Как и в других разделах физики сплошных сред, прежде всего осуществляется переход от реальной среды, состоящей из большого числа отдельных атомов или молекул, к абстрактной сплошной среде, для которой и записываются уравнения движения.

Идеальная среда

Гидродинамика изучает поведение идеальной жидкости — воображаемой среды без вязкости, сил трения и теплопроводности. Касательные напряжения равны нулю. Её можно представить, как систему небольших упругих шаров с пренебрежимо малым объёмом, не прилипающих друг к другу. Они часто сталкиваются друг с другом. Поэтому каждый шар переносит при движении массу, импульс, момент импульса, энергию.

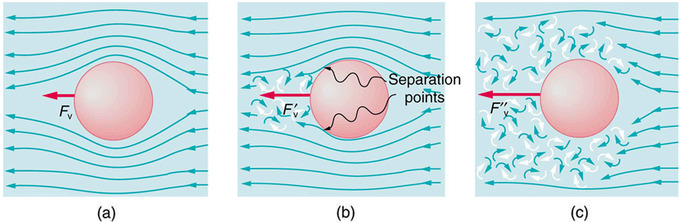
Ламинарное и турбулентное движения жидкости

Экспериментально установлено, что в природе существуют два различных вида движения потока — ламинарное (слоистое, упоря­доченное), при котором отдельные слои жидкости скользят друг относительно друга, и турбулентное (неупорядоченное), когда частицы жидкости движутся по сложным, все время изменяющимся траекториям.

Вследствие этого затрата энергии на турбулентное движение потока больше, чем на ламинарное.

Турбулентность — название такого состояния сплошной среды, газа, жидкости, их смесей, когда в них наблюдаются хаотические колебания мгновенных значений давления, скорости, температуры, плотности относительно некоторых средний значений, за счёт зарождения, взаимодействия и исчезновения в них вихревых движений различных масштабов. Происходит их нелинейное вихревое взаимодействие и распространение в пространстве и времени.

Турбулентность может возникать и при нарушении сплошности среды, например, при кавитации (кипении). При опрокидывании и разрушении волны прибоя возникает многофазная смесь воды, воздуха, пены. Мгновенные параметры среды становятся хаотичными.

Ламинарное течение

Отличие ламинарного течения от турбулентного состоит в характере и направлении водных (газовых) потоков. Они перемещаются слоями, не смешиваясь и без пульсаций. Другими словами, движение проходит равномерно, без беспорядочных скачков давления, направления и скорости.

Ламинарное течение жидкости образуется, например, в узких кровеносных сосудах живых существ, капиллярах растений и в сопоставимых условиях, при течении очень вязких жидкостей (мазута по трубопроводу). Чтобы наглядно увидеть струйный поток, достаточно немного приоткрыть водопроводный кран – вода будет течь спокойно, равномерно, не смешиваясь. Если краник отвернуть до конца, давление в системе повысится и течение приобретет хаотичный характер.

Движение жидкостей называется течением, а совокупность частиц движущейся жидкости — потоком. Графически движение жидкостей изображается с помощью линий тока. Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.

Трубка тока — трубчатая поверхность, ограниченная линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока, называется элементарной струйкой.

Для случая установившегося движения элементарной струйке придаются следующие свойства:

• форма элементарной струйки остается неизменной с течением времени;
• через стенки элементарной струйки движение жидкости не происходит (обмена энергией жидкости между элементарными струйками нет);
• вследствие малости поперечного сечения элементарной струйки скорость и гидродинамическое давление во всех точках ее поперечного сечения одинаковы.

Уравнение неразрывности жидкости

В гидравлике обычно рассматривают потоки, в которых не образуются разрывы. Если выделить в потоке два любых сечения, отстоящих друг от друга на некотором расстоянии, то за время Δ t через сечение S проходит объем жидкости SvΔ t; следовательно, за 1 с через S 1 пройдет объем жидкости S 1 v 1 , где v 1 — скорость течения жидкости в месте сечения S 1 . Через сечение S 2 за 1 с пройдет объем жидкости S 2 v 2 , где v 2 — скорость течения жидкости в месте сечения S 2 . Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема (ρ = const), то через сечение S 2 пройдет такой же объем жидкости, как и через сечение S 1 , т. е.

Произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Соотношение называется уравнением неразрывности для несжимаемой жидкости.

Уравнение Бернулли

При движении идеальной жидкости не происходит превращения механической энергии во внутреннюю, поэтому выполняется закон сохранения механической энергии.

Стационарным принято называть такой поток жидкости, в котором не образуются вихри. В стационарном потоке частицы жидкости перемещаются по неизменным во времени траекториям, которые называются линиями тока. Опыт показывает, что стационарные потоки возникают только при достаточно малых скоростях движения жидкости.

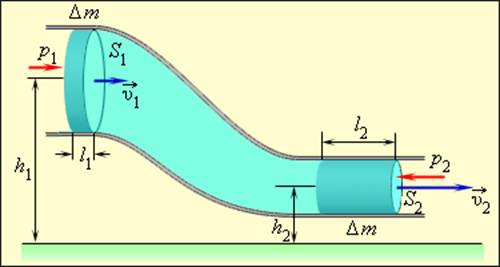
Рассмотрим стационарное движение идеальной несжимаемой жидкости по трубе переменного сечения. Различные части трубы могут находиться на разных высотах. У идеальной жидкости трение полностью отсутствует.

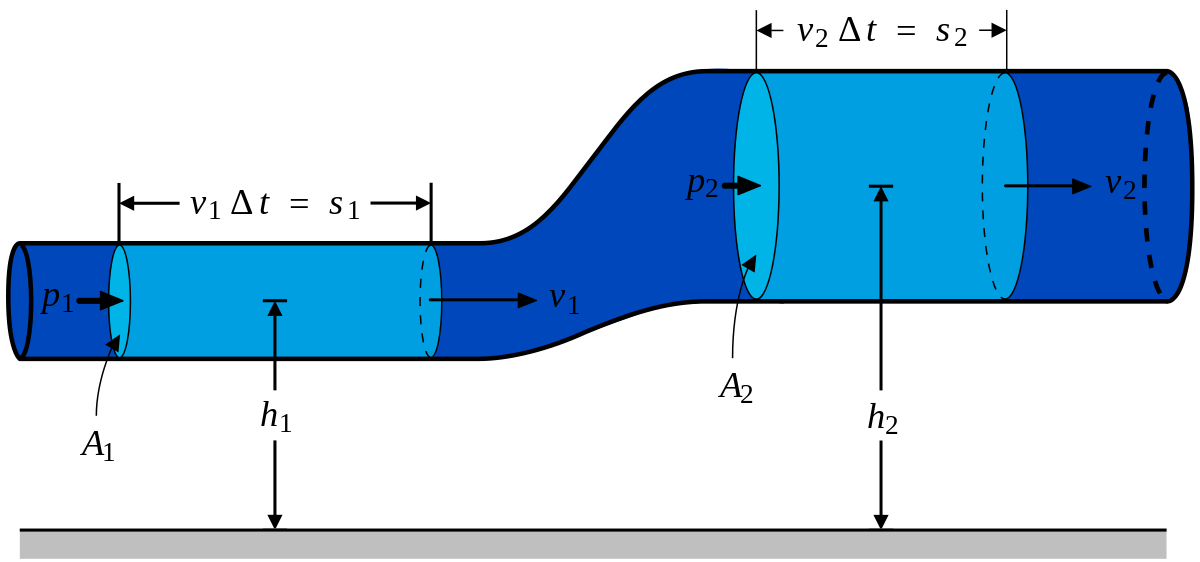
Выделим в стационарно текущей несжимаемой идеальной жидкости трубку тока, ограниченную сечениями S₁ и S₂, по которой жидкость течет слева направо. Пусть в месте сечения S₁ скорость течения v₁ давление р₁ и высота, на которой это сечение расположено, h₁. Аналогично, в месте сечения S₂ скорость течения v₂, давление р₂, высота сечения h₂. За малый промежуток времени Δt жидкость перемещается от сечения S₁ к сечениюS‘₁, от S₂ к S’₂.

Согласно закону сохранения энергии, изменение полной энергии Е₂ — Е₁ идеальной несжимаемой жидкости должно быть равно работе А внешних сил по перемещению массы т жидкости, где

— полные энергии жидкости массой т в местах сечений S₁ и S₂ соответственно.

С другой стороны, А — это работа, совершаемая при перемещении всей жидкости, заключенной между сечениями S₁ и S₂, за рассматриваемый малый промежуток времени Δt:

где р — статическое давление (давление жидкости на поверхность обтекаемого ею тела),

ρv 2 /2 — динамическое давление.

1. Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности следует, что при те чении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в более широких местах, т. е. там, где скорость меньше.

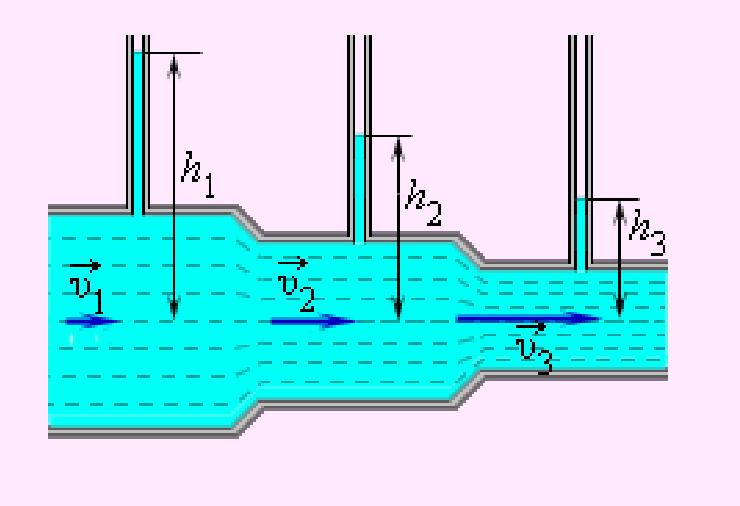
Это можно продемонстрировать, установив вдоль трубы ряд манометров. В соответствии с уравнением Бернулли опыт показывает, что в манометрической трубке В, прикрепленной к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С, прикрепленных к широкой части трубы.

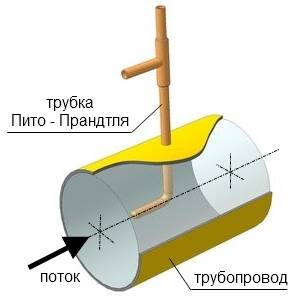
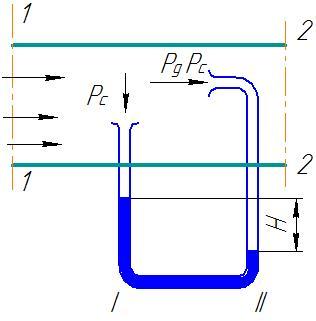
2. Так как динамическое давление связано со скоростью движения жидкости (газа), то уравнение Бернулли позволяет измерять скорость потока жидкости. Для этого применяется трубка Пито — Прандтля. Прибор состоит из двух изогнутых под прямым углом трубок, противоположные концы которых присоединены к манометру. С помощью одной из трубок измеряется полное давление (р₀), с помощью другой — статическое (р).Манометром измеряется разность давлений:

где ρ — плотность жидкости в манометре. С другой стороны, согласно уравнению Бернулли, разность полного и статического давлений равна динамическому давлению:

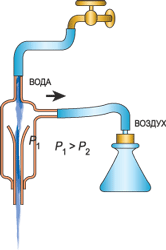
3. Уменьшение статического давления в точках, где скорость потока больше, положено в основу работы водоструйного насоса. Струя воды подается в трубку, открытую в атмосферу, так что давление на выходе из трубки равно атмосферному. В трубке имеется сужение, по которому вода течет с большей скоростью. В этом месте давление меньше атмосферного. Это давление устанавливается и в откачанном сосуде, который связан с трубкой через разрыв, имеющийся в ее узкой части. Воздух увлекается вытекающей с большой скоростью водой из узкого конца. Таким образом можно откачивать воздух из сосуда до давления 100 мм рт. ст. (1 мм рт. ст. = 133,32 Па).

4. Уравнение Бернулли используется для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, в боковой стенке которого на некоторой глубине ниже уровня жидкости имеется маленькое отверстие.

Рассмотрим два сечения (на уровне h₁ свободной поверхности жидкости в сосуде и на уровне h₂ выхода ее из отверстия). Напишем для них уравнение Бернулли:

Так как давления р₁ и р₂ в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. p₁ = p₂ , то уравнение будет иметь вид

Из уравнения неразрывности следует, что v₂/v₁ = S₁/S₂, где S₁ и S₂ — площади поперечных сечений сосуда и отверстия. Если S₁>>S₂, то членом v 2 ₁/2 можно пренебречь и

Это выражение получило название формулы Торричелли .