Стационарное уравнение шредингера свойства оператора полной энергии

Уравнение Шрёдингера

Дуальная корпускулярно-волновая природа квантовых частиц описывается дифференциальным уравнением.

Согласно фольклору, столь распространенному среди физиков, случилось это так: в 1926 году физик-теоретик по имени Эрвин Шрёдингер выступал на научном семинаре в Цюрихском университете. Он рассказывал о странных новых идеях, витающих в воздухе, о том, что объекты микромира часто ведут себя скорее как волны, нежели как частицы. Тут слова попросил пожилой преподаватель и сказал: «Шрёдингер, вы что, не видите, что всё это чушь? Или мы тут все не знаем, что волны — они на то и волны, чтобы описываться волновыми уравнениями?» Шрёдингер воспринял это как личную обиду и задался целью разработать волновое уравнение для описания частиц в рамках квантовой механики — и с блеском справился с этой задачей.

Тут необходимо сделать пояснение. В нашем обыденном мире энергия переносится двумя способами: материей при движении с места на место (например, едущим локомотивом или ветром) — в такой передаче энергии участвуют частицы — или волнами (например, радиоволнами, которые передаются мощными передатчиками и ловятся антеннами наших телевизоров). То есть в макромире, где живём мы с вами, все носители энергии строго подразделяются на два типа — корпускулярные (состоящие из материальных частиц) или волновые. При этом любая волна описывается особым типом уравнений — волновыми уравнениями. Все без исключения волны — волны океана, сейсмические волны горных пород, радиоволны из далеких галактик — описываются однотипными волновыми уравнениями. Это пояснение нужно для того, чтобы было понятно, что если мы хотим представить явления субатомного мира в терминах волн распределения вероятности (см. Квантовая механика), эти волны также должны описываться соответствующим волновым уравнением.

Шрёдингер применил к понятию волн вероятности классическое дифференциальное уравнение волновой функции и получил знаменитое уравнение, носящее его имя. Подобно тому как обычное уравнение волновой функции описывает распространение, например, ряби по поверхности воды, уравнение Шрёдингера описывает распространение волны вероятности нахождения частицы в заданной точке пространства. Пики этой волны (точки максимальной вероятности) показывают, в каком месте пространства скорее всего окажется частица. Хотя уравнение Шрёдингера относится к области высшей математики, оно настолько важно для понимания современной физики, что я его все-таки здесь приведу — в самой простой форме (так называемое «одномерное стационарное уравнение Шрёдингера»). Вышеупомянутая волновая функция распределения вероятности, обозначаемая греческой буквой ψ («пси»), является решением следующего дифференциального уравнения (ничего страшного, если оно вам не понятно; главное — примите на веру, что это уравнение свидетельствует о том, что вероятность ведёт себя как волна):

где x — расстояние, h — постоянная Планка, а m, E и U — соответственно масса, полная энергия и потенциальная энергия частицы.

Картина квантовых событий, которую дает нам уравнение Шрёдингера, заключается в том, что электроны и другие элементарные частицы ведут себя подобно волнам на поверхности океана. С течением времени пик волны (соответствующий месту, в котором скорее всего будет находиться электрон) смещается в пространстве в соответствии с описывающим эту волну уравнением. То есть то, что мы традиционно считали частицей, в квантовом мире ведёт себя во многом подобно волне.

Когда Шрёдингер впервые опубликовал свои результаты, в мире теоретической физики разразилась буря в стакане воды. Дело в том, что практически в то же время появилась работа современника Шрёдингера — Вернера Гейзенберга (см. Принцип неопределенности Гейзенберга), в которой автор выдвинул концепцию «матричной механики», где те же задачи квантовой механики решались в другой, более сложной с математической точки зрения матричной форме. Переполох был вызван тем, что ученые попросту испугались, не противоречат ли друг другу два в равной мере убедительных подхода к описанию микромира. Волнения были напрасны. Сам Шрёдингер в том же году доказал полную эквивалентность двух теорий — то есть из волнового уравнения следует матричное, и наоборот; результаты же получаются идентичными. Сегодня используется в основном версия Шрёдингера (иногда его теорию называют «волновой механикой»), так как его уравнение менее громоздкое и его легче преподавать.

Однако представить себе и принять, что нечто вроде электрона ведёт себя как волна, не так-то просто. В повседневной жизни мы сталкиваемся либо с частицей, либо с волной. Мяч — это частица, звук — это волна, и всё тут. В мире квантовой механики всё не так однозначно. На самом деле — и эксперименты это вскоре показали — в квантовом мире сущности отличаются от привычных нам объектов и обладают другими свойствами. Свет, который мы привыкли считать волной, иногда ведёт себя как частица (которая называется фотон), а частицы вроде электрона и протона могут вести себя как волны (см. Принцип дополнительности).

Эту проблему обычно называют двойственной или дуальной корпускулярно-волновой природой квантовых частиц, причем свойственна она, судя по всему, всем объектам субатомного мира (см. Теорема Белла). Мы должны понять, что в микромире наши обыденные интуитивные представления о том, какие формы может принимать материя и как она себя может вести, просто неприменимы. Сам факт, что мы используем волновое уравнение для описания движения того, что привыкли считать частицами, — яркое тому доказательство. Как уже отмечалось во Введении, в этом нет особого противоречия. Ведь у нас нет никаких веских оснований полагать, будто то, что мы наблюдаем в макромире, должно с точностью воспроизводиться на уровне микромира. И тем не менее дуальная природа элементарных частиц остается одним из самых непонятных и тревожащих аспектов квантовой механики для многих людей, и не будет преувеличением сказать, что все беды начались с Эрвина Шрёдингера.

Уравнение Шредингера

Благодаря толкованию волн, изложенному де Бройлем, и соотношению неопределенностей Гейзенберга можно придти к тому, каким должно быть уравнение движения в рамках теории квантовой механики. Это должно быть равенство, которое описывает движения микрочастиц в силовом поле и из которого были бы видны волновые свойства частиц, наблюдаемые экспериментально. Также оно должно являться уравнением по отношению к волновой функции, поскольку вероятность, с которой частица пребывает в некоторый момент времени в объеме d V в области с координатами x y z , описывается с помощью именно этой величины. Поскольку нужное уравнение иллюстрирует волновые свойства частиц, то он должно само быть волновым уравнением (точно так же, как и уравнение, описывающее электромагнитную волну).

История появление теории

В 1962 г. Шредингер сформулировал положение, позже названное основным уравнением в нерелятивистской квантовой механике, или волновым уравнением Шредингера.

Эрвин Шредингер ( 1887 — 1961 , Австрия) был одним из физиков-теоретиков, которые основали квантовую механику. Он является автором трудов по статистической физике, квантовой теории, биофизике, а также общей теории относительности. Сформулировал основы теории движения микрочастиц – волновой механики (волновая теория Шредингера), а также квантовой теории возмущений (похожий метод в квантовой механике). Лауреат Нобелевской премии.

Отличительной особенностью уравнения Шредингера является то, что оно постулируется, а не выводится. Его истинность подтверждена экспериментально, следовательно, оно может считаться законом природы.

В наиболее общем виде его записывают так:

— h 2 m ∇ 2 Ψ + U ( x , y , z , t ) Ψ = i h ∂ 2 Ψ ∂ t 2 .

Здесь m обозначает массу частицы, i 2 — мнимую единицу, ∇ – так называемый оператор Лапласа, равный ∇ 2 Ψ = ∂ 2 Ψ ∂ x 2 + ∂ 2 Ψ ∂ y 2 + ∂ 2 Ψ ∂ z 2 , Ψ – искомую волновую функцию, а выражение U ( x , y , z , t ) соответствует потенциальной энергии частицы в определенной точке силового поля.

Описание движения частицы в потенциальном поле

Если поле, в котором происходит движение частицы, является потенциальным, то функция U не будет иметь явно выраженной зависимости от времени, и ей можно придать смысл потенциальной энергии. Тогда решить уравнение Шредингера можно разделением на сомножители: один из них будет зависеть только от времени, а второй – только от координаты точки.

Ψ ( x , y , z , t ) = Ψ ( x , y , z ) e — i E h t .

Параметр E обозначает полную энергию частицы. Если поле стационарное, то значение E остается постоянным. Подставив это значение в выражение выше, мы можем убедиться в его справедливости. При этом у нас получится формула Шредингера для стационарных состояний:

— h 2 2 m ∇ 2 Ψ + U Ψ = E Ψ .

∇ 2 Ψ + 2 m h 2 ( E — U ) Ψ = 0 .

Также данное выражение может быть записано в следующем виде:

Преобразование уравнения выполнено с использованием оператора Гамильтона H ^ . Его можно найти, сложив значения операторов — h 2 2 m ∇ 2 + U = H ^ . Гамильтониан – это оператор потенциальной энергии E .

Квантовая механика использует различные операторы также и в качестве других переменных, особенно динамических. Существуют операторы импульса, момента импульса, координат и т.д.

Стационарное уравнение Шредингера

Вы будете перенаправлены на Автор24

Основное уравнение квантовой механики было предложено Э. Шредингером в $1926$ г. Его значение в квантовой физике аналогично значению уравнению движения И. Ньютона. Уравнение Шредингера не выводится, оно постулируется. Его истинность доказывается тем, что полученные с его помощью результаты хорошо согласуются с экспериментами, проводимыми в рамках атомной и ядерной физики. Уравнение Шредингера можно представить в следующем виде:

где $\hbar =\frac<2>=1,05\cdot <10>^<-34>Дж\cdot с\ $- постоянная Планка, $m$ — масса частицы, $U\left(x,y,z,t\right)$- потенциальная энергия частицы в силовом поле в котором перемещается частица, $\triangle =\frac<\partial^2><\partial x^2>+\frac<\partial^2><\partial y^2>+\frac<\partial^2><\partial z^2>$ — оператор Лапласа, $\Psi=\Psi(x,y,z,t)$ — волновая функция частицы, $i=\sqrt<-1>$ — мнимая единица.

Уравнение (1) является справедливым для любой частицы, которая движется со скоростью много меньшей скорости света ($v\ll c,\ где\ c\ $— скорость света в вакууме). Уравнение Шредингера дополняют условиями, которые накладываются на волновую функцию $\Psi\ (x,y,z,t)$:

Данная функция должна быть конечной, непрерывной и однозначной.

Функция $<\left|\Psi\right|>^2$ должна быть интегрируемой, что означает, интеграл $\iiint\limits^<\infty >_<-\infty ><<\left|\Psi\right|>^2dxdydz>$ должен быть конечным. В самом простом случае данное условие сводится к условию нормировки вероятностей. Это условие связано с тем, что физическим смыслом обладает не сама волновая функция, а $<\left|\Psi\right|>^2$.

Значение вышеперечисленных условий в том, что с их помощью не решая уравнения Шредингера, только изучая возможные решения, можно делать ряд важных выводов об энергии и других параметрах рассматриваемой частицы.

Готовые работы на аналогичную тему

Уравнение (1) называют временн$\acute<ы>$м уравнением Шредингера, так как оно содержит производную от волновой функции по времени.

Стационарное уравнение Шредингера

Для большого числа явлений, которые происходят в микромире можно использовать стационарную волновую функцию (независящую от времени) и соответственно стационарное уравнение Шредингера. Такое уравнение имеет смысл для задач, в которых потенциальная энергия не зависит от времени ($U=U\left(x,y,z\right)$).

Решение уравнения (1) найдем в виде:

Подставим выражение (2) в уравнение Шредингера (1), получим:

Разделим обе части выражения (3) на произведение функций $\varphi \Psi$, имеем:

В уравнении (4) левая часть — функция только координат, правая — только времени. Равенство возможно только в случае, если обе части уравнения равны некоторой постоянной. Обозначим ее $-E$ и запишем:

Уравнение (6) называют стационарным уравнением Шредингера. Оно является важным уравнением в квантовой механике и играет основную роль в атомной физике. Функции $\Psi$, которые удовлетворяют уравнению Шредингера при известной U, называют собственными функциями. Величины $E$ при которых существуют решения уравнения Шредингера (6) называют собственными значениями.

Уравнение (5) можно проинтегрировать. Получим:

где $<\varphi >_0=\varphi_0\left(0\right)$- значение $\varphi (t)$ в начальный момент времени (t=0).

Для определения смысла величины $E$ в стационарном уравнении Шредингера уравнение (6) сравнивают с волновым уравнением:

где $v^2_$ — фазовая скорость волн в квадрате. Для синусоидальных волн ($S=A\left(r\right)e^<-i2\pi \nu (t-\frac>)>,\ \ где\ \nu \ —\ частота\ волны$):

уравнение (8) записывается как:

К волнам де Бройля, которые связаны с движущимися частицами, можно применять уравнение (9). Для длины волны де Бройля известно соотношение:

где $v_$- фазовая скорость волн де Бройля, $\nu $ — частота волн де Бройля. Подставим вместо $\frac<\nu >>$ в уравнение (10) в соответствии с (11) величину $\frac$, вместо $S$ волновую функцию, получим:

$\frac<2>=E-U$ — кинетическая энергия частицы, где $E$ — ее полная энергия. Выражение $\frac<4<\pi >^2m^2v^2>$ перепишем как:

Значит в уравнении (12) имеем:

Мы получили уравнение (14) тождественное со стационарным уравнением Шредингера. Рассуждения, приведенные выше, подчеркивают волновой характер уравнения Шредингера. Надо отметить, что представление полной энергии ($E$) как суммы потенциальной и кинетической энергии в квантовой механике имеет ограниченный характер.

Уравнение Шредингера находится в согласии с предположением о связи полной энергии ($E$) частицы с частотой волн де Бройля. Решение уравнения Шредингера можно записать в виде:

Так, состояние частицы в рассматриваемый момент времени можно описать периодической функцией времени, имеющей циклическую частоту ($\omega =\frac<\hbar >$), которая определена полной энергией частицы.

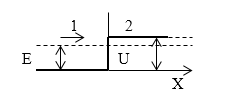
Задание: На пути электронного пучка, имеющего энергию $E$, расположен потенциальный барьер высоты $U$ ($U >E$) (рис.1). Какова относительная вероятность пребывания электрона в области $2$ на расстоянии x от границы областей $1$ и $2$ ($\epsilon$)?

Решение:

В задаче следует найти отношение плотности вероятности нахождения электрона в точке $x$ к плотности вероятности его нахождения на границе областей. В задаче имеется высокий потенциальный барьер бесконечной ширины. Все падающие на барьер электроны отражаются от него, но существует вероятность, что электрон попадет в область $2$. Для нахождения вероятности обнаружения электрона в области $2$ надо решить уравнение Шредингера вида:

Для одномерного случая, который мы имеем для нашей задачи уравнение (1.1) примет вид:

Решение данного уравнения функция:

где $C$ и $D$ постоянные. Однако, из (1.3) при $x\to \infty ,$ то$\ \Psi\to \infty $, что не допустимо, следовательно, $C=0$. Получаем:

Используя (1.4) найдем плотность вероятности нахождения частицы в точке x как:

Плотность вероятности, исходя из (1.5) на границе $^2=D^2$. Тогда относительная вероятность ($\epsilon$) равна:

Задание: Запишите уравнение Шредингера для электрона в водородоподобном атоме.

Решение:

Для написания необходимого уравнения следует вспомнить формулу, определяющую потенциальную энергию, которой обладает электрон в водородоподобном атоме, находящийся на орбите радиуса r:

Уравнение для электрона в водородоподобном атоме должно быть стационарным и его можно записать как:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 06 05 2021