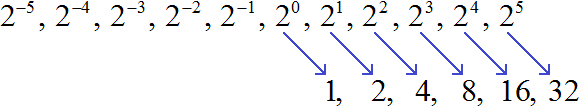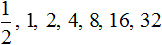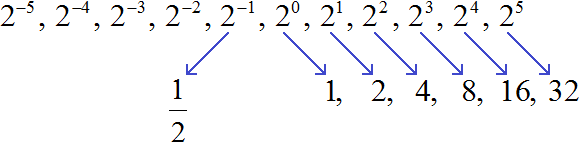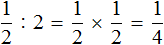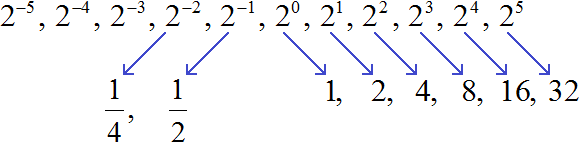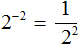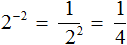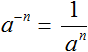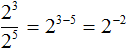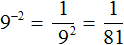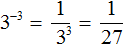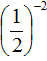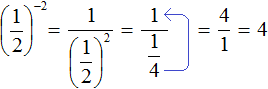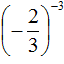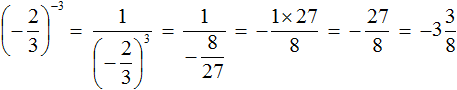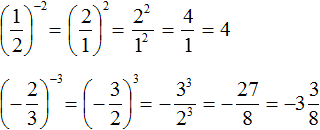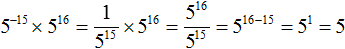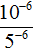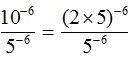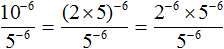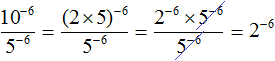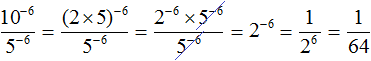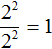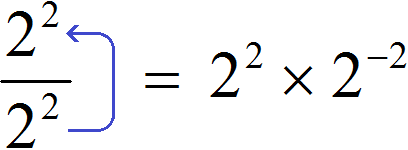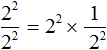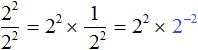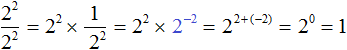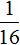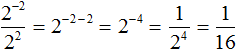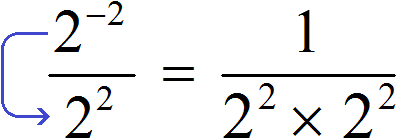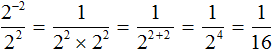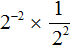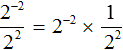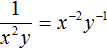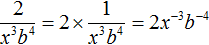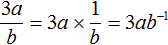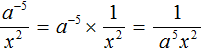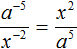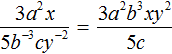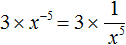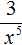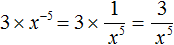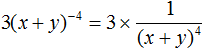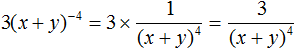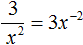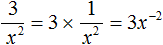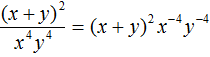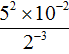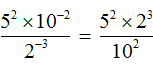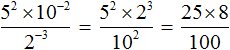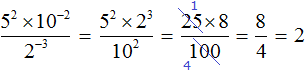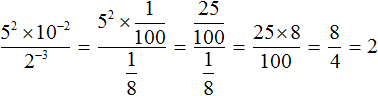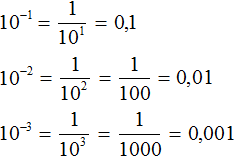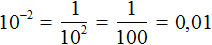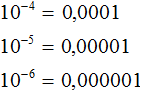Степень с целым показателем уравнения

Как решать
показательные уравнения?

Решение уравнений – навык, который необходим каждому нацеленному на успешную сдачу ЕГЭ и ОГЭ школьнику. Это поможет решить задания №5, 13 и 15 из профильного уровня математики.

Одна из их разновидностей – степенные уравнения, которые иногда также называют показательными. Основная отличительная особенность – наличие переменной \(х\) не в основании степени, а в самом показателе. Как это выглядит:

Не бойтесь – это самый общий вид показательных уравнений. Реальные примеры выглядят как-то так:

Внимательно посмотрите на приведенные уравнения. В каждом из них присутствует, так называемая, показательная (степенная) функция. При решении необходимо помнить об основных свойствах степени, а также использовать особые правила, помогающие вычислить значение \(х\). Познакомиться с понятием степени и ее свойствами можно тут и тут.

И вам понадобится умение решать обыкновенные линейные и квадратные уравнения, те, что вы проходили в 7-8 классе. Вот такие:

И так, любое уравнение, в котором вы увидите показательную (степенную) функцию, называется показательным уравнением. Кроме самой показательной функции в уравнении могут быть любые другие математические конструкции – тригонометрические функции, логарифмы, корни, дроби и т.д. Если вы видите степень, значит перед вам показательное уравнение.

Ура! Теперь знаем, как выглядят показательные уравнения, но толку от этого не очень много. Было бы неплохо научиться их решать. Отличная новость – на наш взгляд показательные уравнения одни из самых простых типов уравнений, по сравнению с логарифмическими, тригонометрическими или иррациональными.

Простейшие показательные уравнения

Давайте начнем с самых простых типов уравнений и разберем сразу несколько примеров:

Что такое решить уравнение? Это значит, что нужно найти такое число, которое при подстановке в исходное уравнение вместо \(х\) даст верное равенство. В нашем примере нужно найти такое число, в которое нужно возвести двойку, чтобы получить восемь. Ну это просто:

Значит, если \(х=3\), то мы получим верное равенство, а значит мы решили уравнение.

Решим что-нибудь посложнее.

Такое уравнение выглядит сложнее. Попробуем преобразовать правую часть уравнения:

Мы применили свойство отрицательной степени по формуле:

Теперь наше уравнение будет выглядеть так:

Заметим, что слева и справа у нас стоят показательные функции, и там, и там основания одинаковые и равны \(3\), только вот степени разные – слева степень \((4х-1)\), а справа \((-2)\). Логично предположить, что если степени у такой конструкции будут равны, при условии, что основания одинаковые, то мы получим верное равенство. Так и поступим:

Такое мы решать умеем, ведь это обыкновенное линейное уравнение.

Поздравляю, мы нашли корень нашего показательного уравнения.

Попробуем поступить так, как в предыдущем примере – преобразуем левую и правую часть, чтобы слева и справа была показательная функция с одинаковым основанием. Как это сделать? Обращаем внимание, что \(125=5*5*5=5^3\), а \(25=5*5=5^2\), подставим:

Воспользуемся одним из свойств степеней \((a^n)^m=a^\):

И опять мы получили две показательные функции, у которых одинаковые основания и для того, чтобы равенство выполнялось, необходимо приравнять из степени:

И еще один пример:

Те, кто хорошо знает свойства степеней, знают, что показательная функция не может быть отрицательной. Действительно, попробуйте возводить \(2\) в различную степень, вы никогда не сможете получить отрицательное число.

Внимание! Показательная функция не может быть отрицательной, поэтому, когда вы встречаете примеры на подобии примера 4, то знайте, что такого быть не может. Здесь корней нет, потому что показательная функция всегда положительна.

Теперь давайте разработаем общий метод решения показательных уравнений. И научимся решать более сложные примеры.

Общий метод решения показательных уравнений

Пусть у нас есть вот такой пример:

Где \(a,b\) какие-то положительные числа. (\(a>0, \; b>0\).

Согласно разобранным выше примерам, логично предположить, что для того, чтобы решить данное уравнение, нужно его преобразовать к виду, где слева и справа стоят показательные функции с одинаковым основанием. Так и поступим.

Слева у нас уже стоит \(a^x\), с этим ничего делать не будем, а вот справа у нас стоит загадочное число \(b\), которое нужно попытаться представить в виде \(b=a^m\). Тогда уравнение принимает вид:

Раз основания одинаковые, то мы можем просто приравнять степени:

Вот и весь алгоритм решения. Просто нужно преобразовать исходное уравнение таким образом, чтобы слева и справа стояли показательные функции с одинаковыми основаниями, тогда приравниваем степени и вуаля – сложное показательное уравнение решено. Осталось только разобраться, как так преобразовывать. Опять разберем на примерах:

Замечаем, что \(16=2*2*2*2=2^4\) это степень двойки:

Основания одинаковые, значит можно приравнять степени:

$$x=4.$$
Пример 6 $$5^<-x>=125 \Rightarrow 5^<-x>=5*5*5 \Rightarrow 5^<-x>=5^3 \Rightarrow –x=3 \Rightarrow x=-3.$$
Пример 7 $$9^<4x>=81 \Rightarrow (3*3)^<4x>=3*3*3*3 \Rightarrow(3^2)^<4x>=3^4 \Rightarrow 3^<8x>=3^4 \Rightarrow 8x=4 \Rightarrow x=\frac<1><2>.$$

Здесь мы заметили, что \(9=3^2\) и \(81=3^4\) являются степенями \(3\).

Все здорово, но проблема в том, что такая схема решения показательных уравнений работает не всегда. Что делать, если привести к одинаковому основанию не получается. Например:

\(3\) и \(2\) привести к одинаковому основанию затруднительно. Но тем не менее мы должны это сделать. Воспользуемся следующей схемой преобразований: пусть есть некоторое положительное число \(b>0\), тогда его можно представить в виде степени любого, нужного вам, положительного числа не равного единице \(a>0, \; a \neq 1\):

Эта очень важная формула, рекомендуем ее выучить. Вернемся к нашему примеру и по формуле представим \(2\) в виде \(3\) в какой-то степени, где \(a=3\), а \(b=2\):

Подставим данное преобразование в наш пример:

Получили равенство двух показательных функций с одинаковым основанием, значит можем приравнять их степени:

Так в ответ и запишем. Никакой ошибки здесь нет, дело в том, что такие логарифмы можно посчитать только на калькуляторе, поэтому на ЕГЭ или в контрольной работе вы просто оставляете ответ в таком виде.

Кто забыл, что такое логарифм, можно посмотреть здесь.

Рассмотрим еще несколько аналогичных примеров.

Те, кто хорошо знает свойства логарифмов, могут поиграться с последней формулой и получить ответ в разном виде:

Все эти варианты ответа верные, их можно смело писать в ответ.

И так, мы с вами научились решать любые показательные уравнения вот такого вида: \(a^x=b\), где \(a>0; \; b>0\).

Но это еще далеко не все. Часто вы будете встречать показательные уравнения гораздо более сложного типа. В ЕГЭ по профильной математике это номер 15 из 2й части. Но бояться тут не нужно, все на первый взгляд сложные уравнения при помощи обычно не самых сложных преобразований сводятся к уравнениям типа \(a^x=b\), где \(a>0; \; b>0\). Рассмотрим типы сложных уравнений, которые могут попасться:

Решение показательных уравнений при помощи замены

Самое первое, что вы должны всегда делать, это пытаться привести все имеющиеся показательные функции к одинаковому основанию.

Здесь это сделать легко, замечаем, что \(9=3^2\), тогда \(9^x=(3^2)^x=3^<2x>=(3^x)^2\). Здесь мы воспользовались свойством степеней: \((a^n)^m=a^\). Подставим:

Обратим внимание, что во всем уравнении все \(х\) «входят» в одинаковую функцию — \(3^x\). Сделаем замену \(t=3^x, \; t>0\), так как показательная функция всегда положительна.

Квадратное уравнение, которое решается через дискриминант:

Оба корня больше нуля, значит оба нам подходят. Сделаем обратную замену и уравнение сводится к решению двух простых показательных уравнений:

И второй корень:

И еще один пример на замену:

Воспользуемся нашим правилом, что все нужно приводить к одинаковому основанию – а стоп, тут и так у всех показательных функций основание \(3\). Давайте еще внимательно посмотрим на наш пример, очень похоже на то, что он тоже делается через замену. Но у нас тут нет одинаковых показательных функций, основания то одинаковые, а вот степени отличаются. Но если быть внимательным, то можно заметить, что в первой степени можно разбить свободный член \(3=2+1\) и вынести общий множитель \(2\):

Подставим в исходное уравнение:

Теперь показательные функции одинаковы и можно сделать замену:

Обратная замена, и наше уравнение сводится к простейшему:

И второе значение \(t\):

Тут у нас две показательные функции с основаниями \(7\) и \(3\), и как сделать из них одинаковые основания непонятно. Этот пример решается при помощи деления. Давайте поделим все наша уравнение на \(3^x\):

Здесь нам придется воспользоваться свойствами степеней:

Разберем каждое слагаемое:

Теперь подставим получившееся преобразования в исходное уравнение:

Теперь видно, что в нашем уравнении есть одинаковая функция, которую можно убрать в замену \(t=(\frac<7><3>)^x\):

Сделаем обратную замену:

И последний пример на замену:

Первым делом нужно сделать так, чтобы все показательные функции были с одинаковым основанием и в идеале с одинаковой степенью. Для этого нам понадобятся формулы для степеней:

Разберем каждое слагаемое нашего уравнения:

Все десятичные дроби всегда разумно представить в виде обыкновенных дробей. И будьте внимательны — отрицательная степень не имеет никакого отношения к знаку показательной функции!

И последнее слагаемое со степенью:

Подставим все наши преобразования в исходное уравнение:

Теперь можно сделать замену \(t=2^x\) или можно обойтись без замены, просто приведя подобные слагаемые (вынести общий множитель \(2^x\)):

Особенно стоит подчеркнуть прием, который мы использовали при решении 13-го примера. Всегда старайтесь избавляться от десятичных дробей. Переводите их в обыкновенные дроби.

И другой тип степенных уравнений, где обычно не нужно делать замену, а необходимо отлично знать все свойства степеней, некоторые из них мы уже обсудили выше. Все про свойства степеней можно посмотреть тут

Вот такое уравнение, в котором у нас, во-первых, показательных функции перемножаются, а еще хуже то, что у них у всех разные основания. Катастрофа, а не пример. Но ничего, все не так страшно, как кажется. Внимательно посмотрите на основания: у нас есть в основании \(2\), \(5\) и \(10\). Очевидно, что \(10=2*5\). Воспользуемся этим и подставим в наше уравнение:

Воспользуемся формулой \((a*b)^n=a^n*b^n\):

И перекинем все показательные функции с основанием \(2\) влево, а с основанием \(5\) вправо:

Сокращаем и воспользуемся формулами \(a^n*a^m=a^\) и \(\frac=a^\):

Самая главная идея при решении показательных уравнений – это любыми доступными способами свести все имеющиеся степенные функции к одинаковому основанию. А еще лучше и к одинаковой степени. Вот почему необходимо знать все свойства степеней, без этого решить уравнения будет проблематично.

Как же понять, где какие преобразования использовать? Не бойтесь, это придет с опытом, чем больше примеров решите, тем увереннее будете себя чувствовать на контрольных в школе или на ЕГЭ по профильной математике. Сначала потренируйтесь на простых примерах и постепенно повышайте уровень сложности. Успехов в изучении математики!

Степень с целым показателем

Степень с целым показателем — это степень, показателем которой является любое целое число.

В прошлом уроке мы изучили степень с натуральным показателем. Этот вид степени тоже является степенью с целым показателем, поскольку натуральные числа относятся к целым числам.

Также, мы рассмотрели степень, показателем которой является 0. Этот вид степени тоже является степенью с целым показателем, поскольку 0 относится к целым числам.

Рассмотрим ещё один вид степени с целым показателем, а именно показателем которой является целое отрицательное число. Выглядят эти степени так:

В дальнейшем любую степень с натуральным, нулевым или целым отрицательным показателем, мы будем называть степенью с целым показателем.

Правило вычисления

Рассмотрим следующую последовательность степеней:

2 0 , 2 1 , 2 2 , 2 3 , 2 4 , 2 5

Первая степень в этой последовательности это степень 2 0 . Предыдущая степень с целым показателем будет уже с отрицательным показателем и выглядеть как 2 −1 .

2 −1 , 2 0 , 2 1 , 2 2 , 2 3 , 2 4 , 2 5

А предыдущая степень с целым показателем, которая располагается до 2 −1 , будет степень 2 −2

2 −2 , 2 −1 , 2 0 , 2 1 , 2 2 , 2 3 , 2 4 , 2 5

Продолжим эту последовательность в сторону степеней с целыми отрицательными показателями:

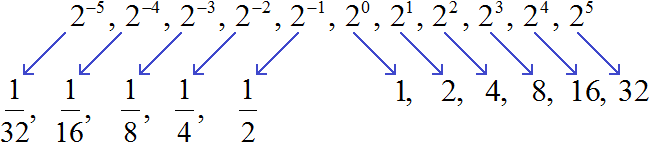
2 −5 , 2 −4 , 2 −3 , 2 −2 , 2 −1 , 2 0 , 2 1 , 2 2 , 2 3 , 2 4 , 2 5

Теперь попробуем вычислить эти степени. Степени с натуральными показателями и степень, показателем которой является 0, вычисляются легко:

А как вычислить степени с отрицательными показателями? Для начала немного отойдём от темы и затронем несколько закономерностей.

В отрицательную степень число возводится немного иначе. Следует понимать, что если при возведении в положительную степень число увеличивается, то при возведении в отрицательную степень это число наоборот уменьшается.

Если мы возьмём какое-нибудь число n , и начнём последовательно увеличивать его степень, то получим последовательность чисел, в которой каждое число меньше следующего в n раз.

Например, возьмём число 2. Начиная с нуля будем последовательно увеличивать его показатель:

2 0 , 2 1 , 2 2 , 2 3 , 2 4 , 2 5

Вычислим эти степени:

Получили последовательность чисел, в которой каждое число меньше следующего числа в 2 раза. Тогда логично предположить, что число, располагающееся до единицы, будет в два раза меньше единицы. Его можно получить, если 1 разделить на 2

Вернёмся к нашей исходной последовательности, где мы вычисляли степени. Получается, что степень 2 −1 мы вычислили. Она равна рациональному числу

Предыдущее за числом должно быть в два раза меньше, чем . Чтобы его получить разделим на 2

Получили . Это значение степени 2 −2

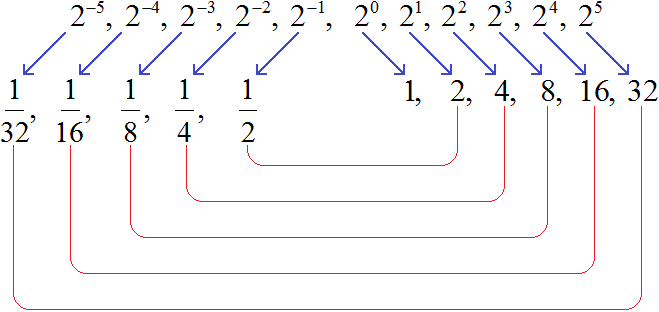
Продолжая деление на 2 можно получить значения остальных степеней с целыми отрицательными показателями:

Заметим, что в данной последовательности значения степеней с отрицательными показателями являются обратными числами к значениям степеней с натуральными показателями:

К примеру, значение степени в 2 2 есть число 4 . А значение степени 2 −2 есть число . Числа 4 и являются обратными друг другу. А степени 2 2 и 2 −2 отличаются только тем, что у них противоположные показатели.

Можно сделать вывод, что для вычисления степени с отрицательным показателем, нужно записать дробь, в числителе которой единица, а в знаменателе та же самая степень, но с противоположным показателем. Покажем это на примере степени 2 −2

Вычислим степень, находящуюся в знаменателе:

Таким образом, чтобы вычислить степень вида a −n можно воспользоваться следующим правилом:

Данное правило можно доказать, используя правило деления степеней с одинаковыми основаниями. Допустим, потребовалось вычислить выражение 2 3 : 2 5 . Запишем это деление в виде дроби

Воспользуемся правилом деления степеней с одинаковыми основаниями:

Получили степень с отрицательным показателем 2 −2 . Ранее мы выяснили, что её значение равно . Чтобы убедиться в этом, попробуем вычислить выражение как обычно, не используя правило деления степеней:

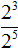
Получили рациональное число 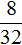. Сократим его на 8. Тогда получим

Пример 2. Найти значение выражения 9 −2

Воспользуемся правилом вычисления степени с целым отрицательным показателем:

Пример 3. Найти значение выражения 3 −3

Следует упомянуть, что правило работает только тогда, когда a ≠ 0 .

Действительно, если a будет равным нулю, то в знаменателе получим 0, а на нуль делить нельзя.

Пример 4. Найти значение выражения

Пример 5. Найти значение выражения

При возведении обыкновенных дробей в отрицательную степень, можно пользоваться формулой 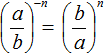. Решим предыдущие два примера с помощью этой формулы:

Желательно уметь возводить обыкновенную дробь в отрицательную степень как с помощью формулы, так и без неё.

Тождественные преобразования

Все тождественные преобразования, которые мы рассматривали при изучении степени с натуральным показателем, сохраняются и для степеней с целыми отрицательными показателями.

Например, чтобы представить выражение 2 −1 × 2 −3 в виде степени, можно воспользоваться основным свойством степени:

2 −1 × 2 −3 = 2 −1 + (−3) = 2 −4

Пример 2. Найти значение выражения 5 −15 × 5 16

Воспользуемся основным свойством степени:

5 −15 × 5 16 = 5 −15 + 16 = 5 1 = 5

Видим, что первый вариант решения намного проще и удобнее.

Пример 3. Найти значение выражения (10 −4 ) −1

Воспользуемся правилом возведения степени в степень:

(10 −4 ) −1 = 10 −4 × (−1) = 10 4 = 10000

Пример 4. Найти значение выражения

Представим число основание 10 в виде произведения 2 × 5 . Тогда числитель примет вид (2 × 5) −6

В числителе применим правило возведения в степень произведения:

Сократим получившуюся дробь на 5 −6

Вычислим степень 2 −6

Поднятие степени из знаменателя в числитель и наоборот

Если знаменатель дробного выражения содержит степень, то данную степень можно поднять в числитель, изменив знак показателя этой степени на противоположный. Значение выражения при этом не меняется. Данное преобразование иногда используется при упрощении выражений.

Рассмотрим следующее равенство:

Данное равенство является верным, поскольку выражение 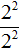равно 2 0 , а любое число в нулевой степени есть единица.

Попробуем поднять степень 2 2 из знаменателя в числитель, изменив знак показателя этой степени на противоположный. При этом, поднятую степень и ту степень, которая располагалась в числителе, соединим знаком умножения:

Получили выражение 2 2 × 2 −2 . Чтобы его вычислить, воспользуемся основным свойством степени:

2 2 × 2 −2 = 2 2 + (−2) = 2 0 = 1

Получился тот же результат, что и раньше. Значит значение выражения не изменилось. Как это работает?

Если в равенстве поменять местами левую и правую часть, то получим равенство . Это позволяет заменять в выражениях дробь вида на тождественно равное ей выражение a −n .

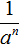
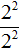
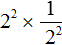
Теперь представим выражение в виде произведения . То есть заменим деление умножением. Напомним, что при замене деления умножением, делимое умножают на число, обратное делителю. А обратное делителю число в данном случае это дробь

Теперь воспользуемся правилом . В произведении заменим дробь на тождественно равное ей выражение 2 −2

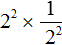
Далее, как и раньше применяем основное свойство степени:

Получился тот же результат 1.

Таким же образом можно опустить степень из числителя в знаменатель, изменив знак показателя этой степени на противоположный.

Рассмотрим выражение 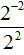. Чтобы найти его значение, воспользуемся правилом деления степеней с одинаковыми основаниями. В результате получим

Теперь попробуем решить этот пример, опустив степень 2 −2 из числителя в знаменатель, изменив знак показателя этой степени на противоположный. При этом, опущенную степень 2 −2 и ту степень, которая располагалась в знаменателе, соединим знаком умножения. А в числителе останется единица:

Дальнейшее вычисление не составит особого труда:

Как и в прошлом примере выражение 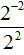представимо в виде произведения

Этим и объясняется появление единицы в числителе, после того как степень 2 −2 была опущена в знаменатель.

Переносимых в знаменатель либо в числитель степеней может быть несколько. Например, знаменатель дроби содержит степени 3 2 , a 3 , b 4 . Перенесём эти степени в числитель, изменив знаки их показателей на противоположные. В результате получим выражение 3 − 2 a − 3 b − 4 .

Пример 2. Поднять степени из знаменателя дроби 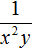в числитель

Пример 3. Поднять степени из знаменателя дроби 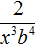в числитель

Пример 4. Поднять степень из знаменателя дроби 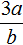в числитель

Пример 5. Опустить степень из числителя дроби 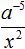в знаменатель

Пример 6. Степень из числителя дроби опустить в знаменатель, а степень из знаменателя поднять в числитель

Представлять дробь в виде произведения вовсе не обязательно. Если пропустить эту запись, то данный пример можно решить короче:

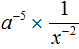
Пример 7. В дроби 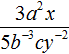перенести из знаменателя в числитель только те степени, которые имеют отрицательные показатели:

Пример 8. Представить произведение 3x −5 в виде дроби, не содержащей степени с отрицательным показателем.

Перепишем произведение 3x −5 с помощью знака умножения:

Сомножитель 3 оставим без изменений, а сомножитель x −5 заменим на тождественно равную ему дробь

Теперь согласно правилу умножения целого числа на дробь, умножим множитель 3 на числитель дроби 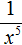. В результате образуется дробь

Пример 9. Представить произведение 3(x + y) −4 в виде дроби, не содержащей степени с отрицательным показателем.

Выражение состоит из сомножителей 3 и (x + y) −4 . Сомножитель 3 оставим без изменений, а сомножитель (x + y) −4 заменим на тождественно равную ему дробь

Теперь умножим множитель 3 на числитель дроби 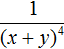. В результате образуется дробь

Пример 10. Представить дробь 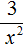в виде произведения.

Чтобы решить этот пример, достаточно поднять степень x 2 в числитель, изменив знак показателя этой степени на противоположный:

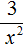
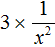
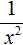
Как и в прошлых примерах дробь можно было представить в виде произведения . Затем воспользовавшись правилом , заменить сомножитель на тождественно равный ему сомножитель x −2 .

Пример 11. Представить дробь 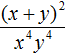в виде произведения.

Пример 12. Найти значение выражения

Поднимем степень 2 −3 из знаменателя в числитель, а степень 10 −2 из числителя опустим в знаменатель:

Вычислим значения степеней, содержащихся в числителе и в знаменателе:

Сократим полученную дробь на 25. Тогда останется дробь , значение которой равно 2.

А если бы мы не подняли степень 2 −3 в числитель, и степень 10 −2 не опустили в знаменатель, а стали вычислять каждую степень по отдельности, то получили бы не очень компактное решение:

Возведение числа 10 в целую отрицательную степень

Число 10 в отрицательную степень возводится таким же образом, как и другие числа. Например:

Замечаем, что количество нулей, которые получаются в ответе равны модулю показателя исходной степени. Например, в степени 10 −2 модуль показателя равен 2 . Это значит, что в ответе будет содержаться два нуля. Так оно и есть:

Чтобы возвести число 10 в отрицательную степень, нужно перед единицей записать количество нулей, равное модулю показателя исходной степени.

При этом после первого нуля следует поставить запятую. Примеры:

Представление чисел 0,1, 0,01, 0,001 в виде степени с основанием 10

Чтобы представить числа 0,1, 0,01, 0,001 в виде степени с основанием 10, нужно записать основание 10, и в качестве показателя указать отрицательный показатель, модуль которого равен количеству нулей исходного числа.

Представим число 0,1 в виде степени с основанием 10. Видим, что в числе 0,1 один нуль. Значит, число 0,1 в виде степени с основанием 10 будет представлено как 10 − 1 . Показатель степени 10 − 1 равен −1. Модуль этого показателя равен количеству нулей в числе 0,1

Число 0,1 это результат деления 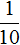, а эта дробь есть значение степени 10 − 1 .

Пример 2. Представить число 0,01 в виде степени с основанием 10.

В числе 0,01 два нуля. Значит, число 0,01 в виде степени с основанием 10 будет представлено как 10 −2 . Показатель степени 10 −2 равен −2. Модуль этого показателя равен количеству нулей в числе 0,01

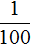
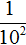
Число 0,01 это результат деления , то есть , а эта дробь есть значение степени 10 −2 .

Пример 3. Представить число 0,001 в виде степени с основанием 10.

Пример 4. Представить число 0,0001 в виде степени с основанием 10.

Пример 5. Представить число 0,00001 в виде степени с основанием 10.

Стандартный вид числа

Запишем число 2 000 000 в виде произведения числа 2 и 1 000 000

Сомножитель 1 000 000 можно заменить на степень 10 6

Такой вид записи называют стандартным видом числа. Стандартный вид числа позволяет записывать в компактном виде как большие, так и маленькие числа.

Например, маленькое число 0,005 можно записать в виде произведения числа 5 и десятичной дроби 0,001 .

Десятичную дробь 0,001 можно заменить на степень с 10 −3

Значит, число 0,005 в стандартном виде будет выглядеть как 5 × 10 −3

По стандартному виду числа можно вычислить изначальное число. Так, при записи числа 2 000 000 в стандартном виде, мы получили произведение 2 × 10 6 . Если вычислить это произведение, то снова получим 2 000 000

2 × 10 6 = 2 × 1 000 000 = 2 000 000

А при записи числа 0,005 в стандартном виде мы получили произведение 5 × 10 −3 . Если вычислить это произведение, то получим 0,005

То есть записывая число в стандартном виде нужно записывать его так, чтобы сохранить его изначальное значение.

Стандартным видом числа называют запись вида a × 10 n , где 1 ≤ a 1 ≤ a . Чаще всего исходное число надо приводить к виду, при котором неравенство 1 ≤ a становится верным.

Например, представим число 12 в стандартном виде. Для начала проверим становится ли верным неравенство 1 ≤ a при подстановке числа 12 вместо а

Неравенство верным не становится. Чтобы сделать неравенство верным, приведём число 12 к виду, при котором оно удовлетворяло бы данному неравенству. Для этого передвинем в числе 12 запятую влево на одну цифру:

Число 12 обратилось в число 1,2. Это число будет удовлетворять неравенству 1 ≤ a

Теперь наша задача состоит в том, чтобы записать произведение a × 10 n . С числом а мы разобрались — этим числом у нас будет 1,2. А как подобрать степень с основанием 10?

После переноса запятой на одну цифру влево, число 12 утратило своё изначальное значение. Запятая на одну цифру влево двигается тогда, когда число делят на 10 . А чтобы восстановить изначальное значение числа запятую нужно передвинуть обратно в правую сторону на одну цифру, то есть умножить число 1,2 на 10 .

Значит, чтобы записать число 12 в стандартном виде, нужно представить его в виде произведения 1,2 × 10¹

Пример 2. Записать число 0,5 в стандартном виде.

Число 0,5 не удовлетворяет неравенству 1 ≤ a a × 10 n . Число a в данном случае это 5. А степень с основанием 10 надо выбрать так, чтобы произведение a × 10 n стало равным числу 0,5. Число 0,5 получится если умножить число 5 на множитель 0,1, который представим в виде степени 10 −1 . В результате получим следующую запись:

Пример 3. Записать число 652 000 в стандартном виде.

Число 652 000 не удовлетворяет неравенству 1 ≤ a , поэтому передвинем запятую в этом числе на пять цифр влево. В результате получим число 6,52000 которое удовлетворяет неравенству 1 ≤ a .

Теперь запишем произведение вида a × 10 n . Число a в данном случае это 6,52000. А степень с основанием 10 надо выбрать так, чтобы произведение a × 10 n стало равным числу 652 000. Число 652 000 получится если число 6,52000 умножить на 100 000, а это есть степень 10 5 . В результате получим следующую запись:

652 000 = 6,52000 × 10 5

Нули в конце десятичной дроби 6,52000 можно отбросить. Тогда получим более компактную запись:

652 000 = 6,52 × 10 5

Пример 5. Записать число 1 024 000 в стандартном виде.

Число 1 024 000 не удовлетворяет неравенству 1 ≤ a , поэтому передвинем запятую в этом числе на шесть цифр влево. В результате получим число 1,024000 которое удовлетворяет неравенству 1 ≤ a .

Теперь запишем произведение вида a × 10 n . Число a в данном случае это 1,024000 . А степень с основанием 10 надо выбрать так, чтобы произведение a × 10 n было равно изначальному числу 1 024 000. Число 1 024 000 получится если число 1,024000 умножить на 1 000 000, а это есть степень 10 6 . В результате получим следующую запись:

1 024 000 = 1,024000 × 10 6

Нули в конце десятичной дроби 1,024000 можно отбросить:

1 024 000 = 1,024 × 10 6

Отбрасывать можно только те нули, которые располагаются в конце, и после которых нет других цифр, бóльших нуля. В приведённом примере были отброшены только три нуля, а нуль располагавшийся между запятой и цифрой 2 был сохранен, несмотря на то, что он тоже располагался после запятой.

Пример 6. Записать число 0,000325 в стандартном виде.

Передвинем в данном числе запятую так, чтобы оно удовлетворяло неравенству 1 ≤ a a × 10 n . Число a в данном случае это 3,25. А степень с основанием 10 надо выбрать так, чтобы произведение a × 10 n было равно изначальному числу 0,000325. Число 0,000325 получится если число 3,25 умножить на множитель 0,0001 который представим в виде степени 10 −4 . В результате получим следующую запись:

Алгебра

План урока:

Определение степени с целым показателем

В 7 классе мы уже изучили степень с натуральным показателем. Напомним, что запись a n означает произведение, состоящее из n множителей, каждый из которых равен a:

Число а именуется основанием степени, а n – это показатель степени. Отдельно напомним, что число в первой степени равно самому себе:

Любое число, кроме нуля, возведенное в нулевую степень, дает единицу:

Сам же ноль в нулевую степень возводить нельзя (так же, как и нельзя делить на ноль).

Математики стремятся по возможности расширить используемые ими понятия. Можно ли сделать показатель степени отрицательным числом? Для этого надо дать новое определение степени. При этом важно, чтобы все уже известные нам правила действий со степенями (их умножение и деление) оставались справедливыми.

При делении степеней их показатели вычитаются, например:

8 15 :8 13 = 8 15 – 13 = 8 2 = 64

Теперь попробуем произвести деление в том случае, когда показатель делимого меньше показателя делителя:

8 15 :8 17 = 8 15 – 17 = 8 – 2

Получили отрицательную степень, смысл которой нам пока не понятен. Выполним это же деление с помощью дробей, при этом учтем, что 8 17 = 8 15 •8 2 :

Итак, мы получили, что

То есть 8 – 2 – это число, обратное 8 2 . Подобные рассуждения помогают сформулировать определение степени с отрицательным показателем:

Напомним, что обратными называются числа, которые при умножении друг на друга дают единицу. Примерами обратных чисел являются:

Вообще для каждой дроби обратной является «перевернутая дробь», поэтому следующие пары чисел являются обратными:

Теперь покажем, как вычислять отрицательную степень числа, пользуясь определением:

Вообще находить отрицательную степень дроби удобней с помощью формулы

Докажем ее справедливость:

Покажем применение этой формулы:

Заметим, что возвести ноль в отрицательную степень не получится. Действительно, если мы попробуем, например, вычислить 0 – 2 , то получим деление на ноль:

Вообще, при возведении нуля в любую отрицательную степень получается деление на ноль, а потому выражение 0 n , где n–отрицательное число, не имеет смысла.

Отрицательные степени очень удобны при работе с некоторыми выражениями. В частности, любую дробь с их помощью можно записать в виде произведения:

Пример: Запишите в виде произведения дробь

Отдельно заметим, формулу, определяющую отрицательную степень

можно и «перевернуть». В ней число 1 выступает в роли делимого, выражение а n – это делитель, а a – n – это частное. Известно, что делитель можно получить, поделив делимое на частное, то есть верна запись

Это значит, что справедливо не только равенство

Свойства степени с целым показателем

Правила действий со степенями, имеющими целый показатель, не отличаются от тех, которые мы изучали ранее. Напомним их.

Убедимся в этом на нескольких примерах:

Однако эти примеры ещё не являются полноценными доказательствами этого свойства степеней. Приведем общее доказательство для того случая, когда число в натуральной степени умножается на число в отрицательной степени:

Также докажем справедливость этого правила и в том случае, когда перемножаются два числа в отрицательной степени:

Для строгого доказательства заменим операцию деления на умножение. Так как

Здесь мы сначала заменяем степень a n на дробь 1/а – n (по определению отрицательной степени), а потом пользуемся тем, что деление на дробь равносильно умножению на «перевернутую дробь».

Продемонстрируем применение этого правила:

Следующие правила позволяют работать со степенями, у которых различаются основания, но совпадают показатели:

Покажем, как это работает:

Для общего случая доказательство будет выглядеть так:

Это правило можно проиллюстрировать так:

Приведем доказательство этого свойства для отрицательных степеней с целым показателем:

Как видим, свойства степеней с целыми показателями (в частности, с отрицательными), не отличаются от уже изученных нами свойств степеней с натуральными показателями. Единственное исключение – добавляется дополнительное ограничение, согласно которому основанием степени с отрицательным целым показателем не может быть ноль. То есть запись 0 – 3 не имеет смысла, хотя выражение 0 3 имеет смысл:

Рассмотрим несколько заданий, в которых необходимо использовать правила работы со степенями

Пример. Представьте в виде степени выражение

у – 8 •у 10

Решение. При перемножении степеней их показатели следует сложить:

у – 8 •у 10 = у – 8 + 10 = у 2

Пример. Вычислите значение выражения

(10 – 1 ) – 6 : (0,1) – 3

(10 – 1 ) – 6 : (0,1) – 3 = 10 (– 1)•(– 6) : (10 – 1 ) – 3 = 10 6 : 10 3 = 10 6 – 3 = 10 3 = 1000

Пример. Представьте число 3 – 36 в виде степени с основанием 9.

3 – 36 = 3 2•(– 18) = 9 – 18

Пример. Представьте произведение 64v – 3 как степень.

64v – 3 = 4 3 v – 3 = (1/4) – 3 v – 3 = (v/4) – 3

Преобразование выражений с целыми степенями

Ранее мы рассматривали понятие рационального выражения. Так называлось выражение, в котором используются 4 основные арифметические операции (в том числе деление), а также возведение в степень. Однако использование отрицательной степени помогает избавиться от операции деления как ненужной. Например, возможны такие преобразования:

Во всех случаях мы заменили деление на возведение в отрицательную степень.

Рассмотрим несколько примеров по преобразованию выражений со степенями.

Пример. Упростите выражение

Решение. Возведение в степень (– 1) означает, по сути, переворачивание дроби:

Пример. Упростите дробь

Решение. Вынесем в числителе множитель а – 3 за скобки

Пример. Представьте в виде дроби выражение

В данном случае мы воспользовались формулой суммы кубов:

a 3 + b 3 = (a + b)(a 2 – ab + b 2 )

Пример. Упростите выражение

(h 2 + ht + t 2 )(h – 2 + h – 1 t – 1 + t – 2 ) – 1

Вынесем из первой скобки множитель h 2 t 2 . При вынесении множителя каждое слагаемое делится на этот самый множитель:

C учетом этого получаем:

(h 2 + ht + t 2 ) = h 2 t 2 (t – 2 + h – 1 t – 1 + h – 2 ) = h 2 t 2 (h – 2 + h – 1 t – 1 + t – 2 )

Зная это, можно записать

(h 2 + ht + t 2 )(h – 2 + h – 1 t – 1 + t – 2 ) – 1 = h 2 t 2 (h – 2 + h – 1 t – 1 + t – 2 )(h – 2 + h – 1 t – 1 + t – 2 ) – 1

В двух скобках стоят одинаковые выражения, но одно из них в степени (– 1). Такие выражения можно сократить, ведь они являются обратными числами:

h 2 t 2 (h – 2 + h – 1 t – 1 + t – 2 )(h – 2 + h – 1 t – 1 + t – 2 ) – 1 = h 2 t 2

Пример. Докажите тождество

Решение. Преобразуем левую часть:

Стандартный вид числа

В физике и других естественных науках изучаются объекты, чьи характеристики (масса, длина, скорость и т.д.) могут измеряться очень большими или очень малыми величинами. Например, масса атома железа равна 0,0000000000000000000000000927 килограмм, а масса Солнца оценивается в 1988500000000000000000000000000 килограмм. Работать с такими числами достаточно неудобно. Сложно даже сравнивать их между собой, ведь для этого надо подсчитывать количество нулей в каждом числе. Поэтому в науке часто используется особая форма чисел, которую называют стандартным видом числа. Он основан на том, что любое число можно записать как произведение числа a, находящегося в пределах от 1 до 10, и какой-нибудь целой (в том числе отрицательной) степени десятки.

Приведем примеры представления чисел в стандартном виде

91 = 9,1•10 = 9,1•10 1

900 = 9•100 = 9•10 2

912 = 9,12•100 = 9,12•10 2

Покажем случаи, когда порядок равен нулю или меньше него

7,63 = 7,63•1 = 7,63•10 0

0,8 = 8•0,1 = 8•10 – 1

0,0875 = 8,75•100 = 8,75•10 – 2

Посмотрите, насколько короче выглядит запись физических величин с использованием стандартного вида:

• масса Солнца: 1988500000000000000000000000000 кг = 1,9885•10 30 кг;
• масса Земли: 5970000000000000000000000 кг = 5,97•10 24 кг;
• масса атома железа: 0,0000000000000000000000000927 = 9,27•10 -26 кг.

Пример. Укажите стандартный вид числа 76000000.

Решение. Первой ненулевой цифрой в записи является семерка, поэтому стандартный вид будет выглядеть так:

где n– какое-то целое число, которое нам надо найти. Поставим в исходном числе запятую после семерки:

Видно, что мы отделили запятой 7 разрядов, то есть перенесли запятую на 7 разрядов вправо. Поэтому n равно 7:

76000000 = 7,6•10 7

Действительно, умножение дробного числа на 10 приводит к смещению запятой на одну позицию влево, поэтому при умножении 7,6 на 10 7 получим 76000000. Наши действия можно проиллюстрировать рисунком:

В случае с числами, меньшими единицы, также надо смотреть на количество разрядов между запятой и первой ненулевой цифрой. Пусть надо представить в стандартном виде десятичную дробь 0,000005605. Значащей частью числа будет 5,605. Для того чтобы получить ее, надо в исходной дроби перенести запятую на 6 разрядов вправо. Поэтому порядок будет равен (– 6):

Теперь попробуем выполнить обратное преобразование – по стандартному виду числа записать его в привычной нам десятичной форме. Пусть есть запись 2,56•10 5 . Для начала искусственно припишем несколько ноликов к значащей части:

Теоретически мы можем дописать любое количество нулей, величина дроби от этого не изменится. Порядок числа равен 5, а потому запятую надо перенести на 5 знаков вправо:

2,5600000•10 5 = 256000,00

Теперь лишние нули после запятой и саму запятую можно и убрать:

Обратите внимание, что порядок числа был равен 5, а в итоге мы получили шестизначное число. Можно сформулировать правило: у числа, имеющего в стандартной виде порядок n, в десятичной представлении перед запятой будет стоять (n + 1)знак. Например:

1,23456789•10 6 = 1234567,89

Здесь порядок числа равен 6, а потому перед запятой стоит 7 знаков.

Напомним, что если число целое и, соответственно, в его записи нет запятой, то ее можно искусственно добавить:

Теперь рассмотрим похожий пример с отрицательным порядком числа. Пусть надо записать в десятичном виде число 9,8765•10 – 4 . Для этого сначала можно условно «подрисовать» нолики перед значащей частью:

Порядок равен (– 4), а потому надо передвинуть запятую на 4 знака влево

Получается, что мы подрисовали слишком много ноликов. Уберем два из нихи получим число в обычной форме:

Вообще, если у числа отрицательный порядок (– n), то первая ненулевая цифра должна оказаться на n-ой позиции после запятой:

Действия с числами в стандартном виде

Стандартный вид чисел удобен тогда, когда есть необходимость сравнивать физические величины, а также перемножать их и делить. Рассмотрим правила сравнения умножения и деления чисел в стандартном виде.

Из двух чисел больше то, у которого больше порядок стандартного вида числа. Так, масса Солнца больше масса Земли, так как у нее порядок равен 30, а у нашей планеты – только 24. Если же порядки одинаковы, то больше то число, у которого больше значащая часть.

Пример. Радиус ядра Солнца оценивается в 1,73•10 8 м, а радиус Юпитера составляет 6,99•10 7 м. Какая из этих величин больше?

Решение. Порядок у радиуса ядра Солнца равен 8, а у Юпитера только 7, поэтому радиус ядра Солнца больше радиуса Юпитера.

Пример. Масса протона составляет 1,673•10 – 27 кг, а масса нейтрона равна 1,675•10 – 27 кг. Какая из этих двух частиц тяжелее?

Решение. У обоих величин одинаковый порядок, равный (– 27). Однако значащая часть у массы нейтрона больше:

Следовательно, нейтрон тяжелее.

Ответ: Нейтрон тяжелее.

Посмотрим, как перемножать числа, находящиеся в стандартном виде. Переставляя множители местами, можно получить:

(a•10 n )•(b•10 m ) = a•b•10 n •10 m = (ab)•10 n+ m

В итоге можно сформулировать правило:

Пример. Земля двигается по своей орбите со средней скоростью 3•10 4 м/с. Какое расстояние она проходит в течение одного невисокосного календарного года (в каждом таком году 31536000 секунд)?

Решение. Переведем количество секунд в году в стандартный вид

31536000 = 3,1536 •10 7

Расстояние (обозначим его как S) равно произведению средней скорости на время:

S = 3•10 4 м/с • 3,1536•10 7 c = 3•3,1536•10 4 + 7 = 9,4608•10 11 м.

Ответ: 9,4608•10 11 м.

Пример. Представьте в стандартном виде произведение чисел 9,5•10 8 и 1,38•10 – 2 .

(9,5•10 8 )•(1,38•10 – 2 ) = (9,5•1,38)•10 8 + (– 2) = 13,11•10 6

Получили число НЕ в стандартном виде, так как 13,11 > 10. Поэтому следует произвести замену 13,11 = 1,311•10:

13,11•10 6 = 1,311•10•10 6 = 1,311•10 7

Теперь попытаемся поделить два числа, находящихся в стандартном виде:

Видно, что справедливо следующее правило:

Пример. Во сколько раз масса Солнца больше массы Земли?

Решение. Выше мы приводили данные, что масса Солнца оценивается в 1,9885•10 30 кг, а масса нашей планеты составляет 5,97•10 24 кг. Поделим массу звезды на массу планеты:

(1,9885•10 30 ):(5,97•10 24 ) = (1,9885:5,97)•10 30 – 24 ≈0,333•10 6 = 333000

Получили, что Солнце примерно в 333 тысячи раз тяжелее Земли.